Functional test for high-dimensional covariance matrix, with application to mitochondrial calcium concentration

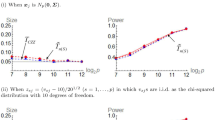
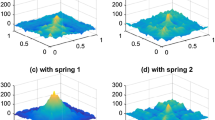
Abstract

In this paper, we present a novel method to test equality of covariance matrices of two high-dimensional samples. The methodology applies the idea of functional data analysis into high-dimensional data study. Asymptotic results of the proposed method are established. Some simulation studies are conducted to investigate the finite sample performance of the proposed method. We illustrate our testing procedures on a mitochondrial calcium concentration data for testing equality of covariance matrices.

Appendix

Denote ${\mathfrak {G}}(t_{1},t_{2},t_{3},t_{4})\equiv {\textsf {E}}\{\varepsilon (t_{1})\varepsilon (t_{2})\varepsilon (t_{3})\varepsilon (t_{4})\}$ and ${\mathfrak {G}}^{*}(t_{1},t_{2},t_{3},t_{4})\equiv {\textsf {E}}\{\varepsilon ^{*}(t_{1}) \varepsilon ^{*}(t_{2})\varepsilon ^{*}(t_{3})\varepsilon ^{*}(t_{4})\}$. To derive the asymptotic properties of the testing method, we make the following assumptions.

• (a) For all $t_{j} \in [0, 1]$, we assume ${\mathfrak {G}}(t_{1},t_{2},t_{3},t_{4})$ and ${\mathfrak {G}}^{*}(t_{1},t_{2},t_{3},t_{4})$ exists.

• (b) Assume $\sup _{t\in [0, 1]}[\mu ^{2}(t)\phi _{l}^{2}(t)]$ and $\sup _{t\in [0, 1]}[\mu ^{* 2}(t)\phi _{l}^{2}(t)]$ are bounded.

• (c) Assume $\mu (t)=\sum _{l=1}^{\infty }\eta _{l}\phi _{l}$ and $\mu ^*(t)=\sum _{l=1}^{\infty }\eta _{l}^*\phi _{l}$, where $\eta _{l}=\int _{0}^{1}\mu (t)\phi _{l}(t)dt$ and $\eta _{l}^*=\int _{0}^{1}\mu ^*(t)\phi _{l}(t)dt$; $\gamma (t,s)=\sum _{l=1}^{\infty }\sum _{l^{'}=1}^{\infty } \rho _{ll^{'}}\phi _{l}\phi _{l^{'}}$ and $\gamma ^{*}(t,s)=\sum _{l=1}^{\infty }\sum _{l^{'}=1}^{\infty } \rho _{ll^{'}}^{*}\phi _{l}\phi _{l^{'}}$, where $\rho _{ll^{'}}=\int _{0}^{1}\int _{0}^{1} \gamma (t,s)\phi _{l}(t)\phi _{l^{'}}(s)dtds$ and $\rho _{ll^{'}}^{*}=\int _{0}^{1}\int _{0}^{1} \gamma ^{*}(t,s)\phi _{l}(t)\phi _{l^{'}}(s)dtds$.

• (d) $\min \{n,m\}\rightarrow \infty$, $\frac{n}{n+m}\rightarrow \alpha$ for a fixed constant $\alpha \in (0,1)$.

• (e) We assume $n/p^{2}\rightarrow 0$.

• (f) All conditions in Chen et al. (2011) are needed.

Assumption (a) is a regular condition in functional data analysis. Assumptions (b), (c) and (e) are used to prove the asymtotic normality of ${\widehat{\rho }}_{ll^{'}}$ and ${\widehat{\rho }}_{ll^{'}}^{*}$. Assumption (d) is a regular condition in two sample test. Assumptions (f) are useful to guarantee high dimensional data which can be converted into a random function.

Lemma 1

Under assumptions 1 and 5, we have

$$\begin{aligned} \begin{array}{lllll} \max \limits _{1\le l\le K}\Vert {\widehat{\phi }}_{j}(s)-\hat{c}_{j}\phi _{j}(s)\Vert =O_{p}\{(n+m)^{-1/2}\}, \end{array} \end{aligned}$$

where $\widehat{c}_{j}=sign({\widehat{\phi }}_{j},\phi _{j})$ and $\widehat{d}_{jk}=sign({\widehat{\phi }}_{jk},\phi _{jk})$.

The Proof of Lemma 1 can easily be obtained by the Lemma 4.3 of Bosq 2000.

Proof of Theorem 1

Firstly, we prove

$$\begin{aligned}&{\widehat{\eta }}_{l}-\eta _{l}=O_{p}(n^{-1/2}),\quad {\widehat{\eta }}_{l}^{*}-\eta _{l}^{*}=O_{p}(m^{-1/2}) \end{aligned}$$

(1)

It can be observed that

$$\begin{aligned} {\widehat{\eta }}_{l}= & {} \frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p}X_{i}(t_{j})\phi _{l}(t_{j}) +\frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p} X_{i}(t_{j})\{{\widehat{\phi }}_{l}(t_{j})-\phi _{l}(t_{j})\}\nonumber \\\equiv & {} A_{1}+A_{2}. \end{aligned}$$

(2)

For $A_{1}$, because of $X_{i}(t)= \mu (t) + \varepsilon _{i}(t)$ we have

$$\begin{aligned} A_{1}= & {} \frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p} \varepsilon _{i}(t_{j})\phi _{l}(t_{j}) +\frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p} \mu (t_{j})\phi _{l}(t_{j})\nonumber \\\equiv & {} A_{11}+A_{12}. \end{aligned}$$

(3)

It is easy to see that $A_{11}$ is the average of independent identically distributed random variables with mean ${\textsf {E}}(A_{11})=0$ and variance ${\textsf {Var}}(A_{11})=\frac{1}{n}\lambda _{l}$. By the central limit theorem, we obtain

$$\begin{aligned} A_{11}\xrightarrow {d}N(0,\lambda _{l}). \end{aligned}$$

(4)

where

$$\begin{aligned} \lambda _l= & {} \int _{0}^{1}\int _{0}^{1}\phi _{l}(t) \gamma (t,s)\phi _{l}(s) dtds, \\ \end{aligned}$$

By Assumptions (c), we have

$$\begin{aligned} A_{12}-\eta _{l} =O(p^{-1}) \end{aligned}$$

(5)

By (4) and (5) and Assumption (e), we have

$$\begin{aligned} A_{1}-\eta _{l} =O_{p}(n^{-1/2}) \end{aligned}$$

(6)

For $A_{2}$, we have

$$\begin{aligned} A_{2}= & {} \frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p}\mu (t_{j}) \{{\widehat{\phi }}_{l}(t_{j})-\phi _{l}(t_{j})\} +\frac{1}{np}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{p} \varepsilon _{i}(t_{j})\{{\widehat{\phi }}_{l}(t_{j})-\phi _{l}(t_{j})\}\\\equiv & {} A_{21}+A_{22}. \end{aligned}$$

For $A_{21}$, we have

$$\begin{aligned} \begin{array}{lllll} &{}\text {E} A_{21}^{2}\\ &{}\le {\displaystyle \frac{1}{n^2}}\sum \limits _{i=1}^{n}{\displaystyle \frac{1}{p^{2}}} \sum \limits _{j=1}^{p} \{\mu ^{2}(t_{j}) \text {E}[{\widehat{\phi }}_{j}(t_{j})-\phi _{l}(t_{j})]^{2}\}\\ &{}\ \ + {\displaystyle \frac{1}{n^2}}\sum \limits _{i=1}^{n}{\displaystyle \frac{1}{p(p-1)}} \sum \limits _{j_{1}\ne j_{1}^{'}} \{\mu (t_{j_{1}})\mu (t_{j_{1}^{'}}) \times \text {E}[{\widehat{\phi }}_{l}(t_{j_{1}})- \phi _{l}(t_{j_{1}})] [{\widehat{\phi }}_{l}(t_{j_{1}^{'}})-\phi _{l}(t_{j_{1}^{'}})] \}\\ &{}\equiv A_{211}+A_{212} \end{array} \end{aligned}$$

For $A_{211}$, by Assumption 4 and Lemma 1, we have

$$\begin{aligned} \begin{array}{lllll} A_{211} &{}\le \sup \limits _{t\in {\mathcal {T}}}\mu ^{2}(t) {\displaystyle \frac{c}{n^2}}\sum \limits _{i=1}^{n}{\displaystyle \frac{1}{p^{2}}} \sum \limits _{l_{1}=1}^{p} \text {E}[{\widehat{\phi }}_{j}(t_{j_{1}})-\phi _{j}(t_{j_{1}})]^{2}\}\\ &{}=O(\frac{1}{np}) \end{array} \end{aligned}$$

(7)

According to Cauchy-Schwartz inequality, we have

$$\begin{aligned} A_{212}= & {} O(\frac{1}{np}) \end{aligned}$$

Then, we have $A_{2}=O_{p}(\frac{1}{np})$.

According to Assumption (e), we obtain ${\widehat{\eta }}_{l}- \eta _{l}=O_{p}(n^{-1/2})$. Similarly, we can prove ${\widehat{\eta }}_{l}^{*}- \eta _{l}^{*}=O_{p}(m^{-1/2})$. The proof of (1) is then completed.

Secondly, we prove $T_{n,m}\xrightarrow {d}\chi _{K^{2}}^{2}$ under $H_0$. If we can prove that

$$\begin{aligned} \begin{array}{lllll} \sqrt{n}({\widehat{\rho }}_{ll^{'}}-\rho _{ll^{'}}) \xrightarrow {d}N(0,\lambda _{ll^{'}}), ~~\sqrt{m}({\widehat{\rho }}_{ll^{'}}^*-\rho _{ll^{'}}^*) \xrightarrow {d}N(0,\lambda _{ll^{'}}^*). \end{array} \end{aligned}$$

(8)

where

$$\begin{aligned} \lambda _{ll^{'}}= & {} \int _{0}^{1}\int _{0}^{1} \int _{0}^{1}\int _{0}^{1}{\mathfrak {G}}(t_{j_{1}}, t_{j_{2}}, t_{j_{3}}, t_{j_{4}}) \phi _{l}(t_{j_{1}}) \phi _{l}(t_{j_{2}}) \phi _{l^{'}}(t_{j_{3}}) \phi _{l^{'}}(t_{j_{4}}), \\ \lambda _{ll^{'}}^{*}= & {} \int _{0}^{1}\int _{0}^{1} \int _{0}^{1}\int _{0}^{1}{\mathfrak {G}}^{*}(t_{j_{1}}, t_{j_{2}}, t_{j_{3}}, t_{j_{4}}) \phi _{l}(t_{j_{1}}) \phi _{l}(t_{j_{2}})\phi _{l^{'}}(t_{j_{3}}) \phi _{l^{'}}(t_{j_{4}}). \end{aligned}$$

Then together with Slutsky’s Lemma, the first part of Theorem 1 can be proved easily. Therefore, our attention now focuses on proving the first result of (8).

It can be observed that

$$\begin{aligned} {\widehat{\rho }}_{ll^{'}}= & {} \frac{1}{np^{2}}\sum \limits _{i=1}^{n}\left\{ \sum _{j_{1}=1}^{p} [X_{i}(t_{j_{1}}){\widehat{\phi }}_{l}(t_{j_{1}})-{\widehat{\eta }}_{l}] \sum _{j_{2}=1}^{p}[X_{i}(t_{j_{2}}) {\widehat{\phi }}_{l^{'}}(t_{j_{2}})-{\widehat{\eta }}_{l^{'}}]\right\} \\= & {} \frac{1}{np^{2}}\sum \limits _{i=1}^{n}\left\{ \sum _{j_{1}=1}^{p}\sum _{j_{2}=1}^{p} \varepsilon _{i}(t_{j_{1}}) \varepsilon _{i}(t_{j_{2}}){\widehat{\phi }}_{l}(t_{j_{1}}) {\widehat{\phi }}_{l^{'}}(t_{j_{2}})\right\} \\&+\frac{1}{np^{2}}\sum \limits _{i=1}^{n}\left\{ \sum _{j_{1}=1}^{p} \varepsilon _{i}(t_{j_{1}}){\widehat{\phi }}_{l}(t_{j_{1}}) \left[ \sum _{j_{2}=1}^{p}\mu (t_{j_{2}}){\widehat{\phi }}_{l^{'}}(t_{j_{2}}) -{\widehat{\eta }}_{l^{'}}\right] \right\} \\&+\frac{1}{np^{2}}\sum \limits _{i=1}^{n}\left\{ \sum _{j_{2}=1}^{p} \varepsilon _{i}(t_{j_{2}}){\widehat{\phi }}_{l^{'}}(t_{j_{2}}) \left[ \sum _{j_{1}=1}^{p}\mu (t_{j_{1}}){\widehat{\phi }}_{l}(t_{j_{1}}) -{\widehat{\eta }}_{l}\right] \right\} \\&+\frac{1}{np^{2}}\sum \limits _{i=1}^{n}\left\{ \left[ \sum _{j_{1}=1}^{p} \mu (t_{j_{1}}){\widehat{\phi }}_{l}(t_{j_{1}}) -{\widehat{\eta }}_{l}\right] [\sum _{j_{2}=1}^{p}\mu (t_{j_{2}}){\widehat{\phi }}_{l^{'}}(t_{j_{2}}) -{\widehat{\eta }}_{l^{'}}]\right\} \\\equiv & {} B_{1}+B_{2}+B_{3}+B_{4}. \end{aligned}$$

It is easy to see that $B_{1}-\rho _{ll^{'}}$ is the average of independent identically distributed random variables with mean 0 and variance $\frac{1}{n}\lambda _{ll^{'}}$. By the central limit theorem,

$$\begin{aligned} \begin{array}{lllll} \sqrt{n} (B_{1}-\rho _{ll^{'}})\xrightarrow {d}N(0,\lambda _{ll^{'}}). \end{array} \end{aligned}$$

(9)

Next, we analyze the term $B_{2}$. In fact, by (1), we have

$$\begin{aligned}&\sup _{i=1,\ldots ,n}\left\{ \frac{1}{p}\sum _{j_{2}=1}^{N} \mu (t_{j_{2}}){\widehat{\phi }}_{l^{'}}(t_{j_{2}}) -{\widehat{\eta }}_{l^{'}}\right\} \\&\quad =\sup _{i=1,\ldots ,n} \left\{ \frac{1}{p}\sum _{j_{2}=1}^{N}\mu (t_{j_{2}}) {\widehat{\phi }}_{l^{'}}(t_{j_{2}}) -\eta _{l^{'}}\right\} +O_{p}(p^{-1})\\&\quad =O_{p}(n^{-1/2}) \end{aligned}$$

According to (1), we have

$$\begin{aligned} \frac{1}{np}\sum \limits _{i=1}^{n}\left\{ \sum _{j_{1}=1}^{p} \varepsilon _{i}(t_{j_{1}})\phi _{l}(t_{j_{1}})\right\} = O_{p}(n^{-1/2}). \end{aligned}$$

According to Assumption (b) and the results in Kraus (2015), we have $B_{2}=o_{p}(n^{-1/2})$. Using the arguments similar to that of $B_2$, we have

$$\begin{aligned} \begin{array}{lllll} B_{3} =o_{p}(n^{-1/2}). \end{array} \end{aligned}$$

(10)

Similarity, we can prove

$$\begin{aligned} \begin{array}{lllll} B_{4} =o_{p}(n^{-1/2}). \end{array} \end{aligned}$$

(11)

Combing the above discussions, we obtain

$$\begin{aligned} \begin{array}{lllll} \sqrt{n}({\widehat{\rho }}_{ll^{'}}-\rho _{ll^{'}}) \xrightarrow {d}N(0,\lambda _{ll^{'}}) \end{array} \end{aligned}$$

(12)

Similarly, we can prove $\sqrt{n}({\widehat{\rho }}_{ll^{'}}^{*}-\rho _{ll^{'}}^{*}) \xrightarrow {d}N(0,\lambda _{ll^{'}}^{*})$. The proof of Theorem 1 is completed. $\square$

Proof of Theorem 2

According to the results in the above proof, we have for $l=1, \ldots , K$ and $l^{'}=1, \ldots , K$,

$$\begin{aligned} {\widehat{\rho }}_{ll^{'}}\xrightarrow {p} \rho _{ll^{'}}, {\widehat{\rho }}_{ll^{'}}^{*}\xrightarrow {p} \rho _{ll^{'}}^{*}. \end{aligned}$$

Then it yields that

$$\begin{aligned} \sum _{l=1}^{K}\sum _{l^{'}=1}^{K}\frac{[{\widehat{\rho }}_{ll^{'}}- {\widehat{\rho }}_{ll^{'}}^*]^{2}}{{\widehat{\lambda }}_{ll^{'}}}- \sum _{l=1}^{K}\frac{[\rho _{ll^{'}}- \rho _{ll^{'}}^*]^{2}}{\lambda _{ll^{'}}}\xrightarrow {p} 0. \end{aligned}$$

Therefore, under $H_A$ and Assumption (d), we have

$$\begin{aligned} T_{n,m} = \frac{nm}{n+m}\sum _{l=1}^{K}\sum _{l^{'}=1}^{K}\frac{({\widehat{\rho }}_{ll^{'}}- {\widehat{\rho }}_{ll^{'}}^*)^{2}}{\widetilde{\lambda }_{ll^{'}}} \xrightarrow {p} \frac{nm}{n+m}\sum _{l=1}^{K}\frac{(\rho _{ll^{'}}- \rho _{ll^{'}}^*)^{2}}{{\lambda }_{ll^{'}}}\rightarrow \infty . \end{aligned}$$

Then Theorem 2 is proved. $\square$