Linearity tests and stochastic trend under the STAR framework

Abstract

This study investigates the linearity test of smooth transition autoregressive models when the true data generating process is a stochastic trend process. Results show that, under the null hypothesis of linearity, the asymptotic distribution of the W statistic proposed by Teräsvirta (J Am Stat Assoc 89:208–218, 1994) follows the χ² distribution, whereas the finite sample distribution does not. A maximized Monte Carlo simulation-based test is used to perform the linearity test, and the results show good performance.

Appendix

1.1 Proof of Theorem 1

According to Eq. (2) and the assumption of Theorem 1, when the true DGP is a stochastic trend $y_{t} = a_{0} + y_{t - 1} + \varepsilon_{t} ,\;a_{0} \ne 0.$ This equation implies that y_t = a₀t + y₀ + ξ_t, ξ_t = ∑ɛ_t. Thus, we obtain

$$ T^{ - (i + 1)} \sum {y_{t - 1}^{i} } \mathop{\longrightarrow}\limits{p}\frac{{a_{0}^{i} }}{i + 1},\quad i = 1,\;2, \ldots ,8. $$

(10)

Let $\varUpsilon_{1} ,\;\tilde{\varUpsilon }_{1}$ be the scaling matrix, Υ₁ = diag(T^1/12.2, T^3/32.2, T^5/52.2, T^7/72.2, T^9/92.2), $\tilde{\varUpsilon }_{1} = diag(T^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} ,\;T^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0pt} 2}}} ,\;T^{{{9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0pt} 2}}} ),$ and $\tilde{\varUpsilon }_{1} {\mathbf{R}}_{1} = {\mathbf{R}}_{1} \varUpsilon_{1} ,$ ${\mathbf{R}}_{1} = \left[ {\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right].$ Let X be the matrix of independent variables in Eq. (2), β the coefficient vector, b_T the OLS estimate of β, and ɛ the error vector. Thus, we obtain

$$ \left[ {\varUpsilon_{1}^{ - 1} ({\mathbf{X}}^{'} {\mathbf{X}})\varUpsilon_{1}^{ - 1} } \right]\mathop{\longrightarrow}\limits{p}\left[ {\begin{array}{ccccc} 1 & {\frac{a}{2}} & {\frac{{a^{2} }}{3}} & {\frac{{a^{3} }}{4}} & {\frac{{a^{4} }}{5}} \\ {\frac{a}{2}} & {\frac{{a^{2} }}{3}} & {\frac{{a^{3} }}{4}} & {\frac{{a^{4} }}{5}} & {\frac{{a^{5} }}{6}} \\ {\frac{{a^{2} }}{3}} & {\frac{{a^{3} }}{4}} & {\frac{{a^{4} }}{5}} & {\frac{{a^{5} }}{6}} & {\frac{{a^{6} }}{7}} \\ {\frac{{a^{3} }}{4}} & {\frac{{a^{4} }}{5}} & {\frac{{a^{5} }}{6}} & {\frac{{a^{6} }}{7}} & {\frac{{a^{7} }}{8}} \\ {\frac{{a^{4} }}{5}} & {\frac{{a^{5} }}{6}} & {\frac{{a^{6} }}{7}} & {\frac{{a^{7} }}{8}} & {\frac{{a^{8} }}{9}} \\ \end{array} } \right] \equiv {\mathbf{Q}}_{1} , $$

(11)

$$ \left\{ {\varUpsilon_{1}^{ - 1} ({\mathbf{X}}^{'} {\varvec{\upvarepsilon}})} \right\} = \left[ {\begin{array}{ccccc} {T^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \sum {\varepsilon_{t} } } & {T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1} } \varepsilon_{t} } & {T^{{ - {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{2} } \varepsilon_{t} } & {T^{{ - {7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{3} } \varepsilon_{t} } & {T^{{ - {9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{4} } \varepsilon_{t} } \\ \end{array} } \right]^{\prime } \equiv {\mathbf{h}}_{1} . $$

(12)

All h₁ elements follow a Gaussian distribution, i.e.,

$$ \begin{aligned} & T^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \sum {\varepsilon_{t} } \Rightarrow N(0,\;\sigma^{2} ),\quad T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a_{0}^{2} }}{3}\sigma^{2} } \right),\quad T^{{ - {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{2} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a_{0}^{4} }}{5}\sigma^{2} } \right), \\ & T^{{ - {7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{3} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a_{0}^{4} }}{7}\sigma^{2} } \right),\quad T^{{ - {9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1}^{4} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a_{0}^{8} }}{9}\sigma^{2} } \right). \\ \end{aligned} $$

Here, only the proof of $T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a_{0}^{2} }}{3}\sigma^{2} } \right)$ is given, and others can be readily obtained.

$$ T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1} } \varepsilon_{t} = T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {[a_{0} (t - 1)} + \xi_{t} + y_{0} ]\varepsilon_{t} = a_{0} T^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \sum {{{(t} \mathord{\left/ {\vphantom {{(t} T}} \right. \kern-0pt} T}} )\varepsilon_{t} + o_{p} (T^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ). $$

(13)

Clearly, t/Tɛ_t is a martingale difference sequence with a variance of $\sigma_{t}^{2} = E\left( {t/T\varepsilon_{t} } \right)^{2} = t^{2} /T^{2} \sigma^{2} .$ Some conditions are satisfied, i.e., $\frac{1}{T}\sum {\sigma_{t}^{2} } = \frac{1}{T}\sum {t^{2} /T^{2} \sigma^{2} } \to \frac{1}{3}\sigma^{2} ,$ $\frac{1}{T}\sum {(t/T\varepsilon_{t} )^{2} } \mathop{\longrightarrow}\limits{p}\frac{1}{3}\sigma^{2} ,$ and E(t/Tɛ_t)^r < ∞ for some r > 2 and all t. Thus, according to White (1984, Corollary 5.25), we obtain $T^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sum {y_{t - 1} } \varepsilon_{t} \Rightarrow N\left( {0,\;\frac{{a^{2} }}{3}\sigma^{2} } \right).$

Consider the joint distribution of the h₁ elements. Any linear combination of these five elements takes the following form:

$$ \begin{aligned} T^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \sum {(\lambda_{1} + \lambda_{2} T^{ - 1} y_{t - 1} + \lambda_{3} T^{ - 2} y_{t - 1}^{2} + \lambda_{4} T^{ - 3} y_{t - 1}^{3} + \lambda_{5} T^{ - 4} y_{t - 1}^{4} )} \varepsilon_{t} \hfill \\ \xrightarrow{p}T^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \sum {\left( {\lambda_{1} + \lambda_{2} \frac{at}{T} + \lambda_{3} \frac{{a^{2} t^{2} }}{{T^{2} }} + \lambda_{4} \frac{{a^{3} t^{3} }}{{T^{3} }} + \lambda_{5} \frac{{a^{4} t^{4} }}{{T^{4} }}} \right)} \varepsilon_{t} . \hfill \\ \end{aligned} $$

(14)

Moreover, $\left( {\lambda_{1} + \lambda_{2} \frac{at}{T} + \lambda_{3} \frac{{a^{2} t^{2} }}{{T^{2} }} + \lambda_{4} \frac{{a^{3} t^{3} }}{{T^{3} }} + \lambda_{5} \frac{{a^{4} t^{4} }}{{T^{4} }}} \right)\varepsilon_{t}$ is a martingale difference sequence with a positive variance given by

$$ \begin{aligned} \sigma_{t}^{2} & = E\left( {\lambda_{1} + \lambda_{2} \frac{at}{T} + \lambda_{3} \frac{{a^{2} t^{2} }}{{T^{2} }} + \lambda_{4} \frac{{a^{3} t^{3} }}{{T^{3} }} + \lambda_{5} \frac{{a^{4} t^{4} }}{{T^{4} }}} \right)^{2} \varepsilon_{t}^{2} \\ & = \sigma^{2} \left( {\lambda_{1}^{2} + \lambda_{2}^{2} \frac{{a^{2} t^{2} }}{{T^{2} }} + \lambda_{3}^{2} \frac{{a^{4} t^{4} }}{{T^{4} }} + \lambda_{4}^{2} \frac{{a^{6} t^{6} }}{{T^{6} }} + \lambda_{5}^{2} \frac{{a^{8} t^{8} }}{{T^{8} }}} \right. \\ & \quad + 2\lambda_{1} \lambda_{2} \frac{ta}{T} + 2\lambda_{1} \lambda_{3} \frac{{a^{2} t^{2} }}{{T^{2} }} + 2\lambda_{1} \lambda_{4} \frac{{a^{3} t^{3} }}{{T^{3} }} + 2\lambda_{1} \lambda_{5} \frac{{a^{4} t^{4} }}{{T^{4} }} \\ & \quad + 2\lambda_{2} \lambda_{3} \frac{{a^{3} t^{3} }}{{T^{3} }} + 2\lambda_{2} \lambda_{4} \frac{{a^{4} t^{4} }}{{T^{4} }} + 2\lambda_{2} \lambda_{5} \frac{{a^{5} t^{5} }}{{T^{5} }} + 2\lambda_{3} \lambda_{4} \frac{{a^{5} t^{5} }}{{T^{5} }} \\ & \quad + \left. {2\lambda_{3} \lambda_{5} \frac{{a^{6} t^{6} }}{{T^{6} }} + 2\lambda_{4} \lambda_{5} \frac{{a^{7} t^{7} }}{{T^{7} }}} \right) \\ \end{aligned} $$

(15)

and $\frac{1}{T}\sum {\sigma_{t}^{2} } \to \sigma^{2} {\mathbf{\lambda^{\prime}Q}}_{1} {\varvec{\uplambda}}.$ Furthermore,

$$ \frac{1}{T}\sum {\left( {\lambda_{1} + \lambda_{2} \frac{at}{T} + \lambda_{3} \frac{{a^{2} t^{2} }}{{T^{2} }} + \lambda_{4} \frac{{a^{3} t^{3} }}{{T^{3} }} + \lambda_{5} \frac{{a^{4} t^{4} }}{{T^{4} }}} \right)^{2} \varepsilon_{t}^{2} } \mathop{\longrightarrow}\limits^{p}\sigma^{2} {\varvec{\lambda}}^{\prime}\varvec{Q}_{1} {\varvec{\uplambda}},$$

(16)

where λ = [λ₁λ₂λ₃λ₄λ₅]′. Thus, any linear combination of the five h₁ elements is asymptotically Gaussian, which implies a joint Gaussian distribution of h₁ according to the Cramer–Wold theorem. Thus, h₁ ⇒ N(0, σ²Q₁) and

$$ \varUpsilon_{1} ({\mathbf{b}}_{T} - {\varvec{\upbeta}}) = \left[ {\varUpsilon_{1}^{ - 1} ({\mathbf{X^{\prime}X}})\varUpsilon_{1}^{ - 1} } \right]^{ - 1} \varUpsilon_{1}^{ - 1} {\mathbf{X}}^{\prime}{\varvec{\upvarepsilon}}\Rightarrow N\left( {0,\;\sigma^{2} {\mathbf{Q}}_{1}^{ - 1} } \right). $$

(17)

The limiting distribution of statistic W can be derived by

$$\begin{aligned} W = & \,({\mathbf{b}}_{T} - {\varvec{\upbeta }})^{'} {\mathbf{R}}^{'} _{1} \left\{ {{\mathbf{R}}_{1} s_{T} ^{2} ({\mathbf{X}}^{{\mathbf{'}}} {\mathbf{X}})^{{ - 1}} {\mathbf{R}}^{'} _{1} } \right\}^{{ - 1}} {\mathbf{R}}_{1} ({\mathbf{b}}_{T} - {\varvec{\upbeta }}) \\ = & \,({\mathbf{b}}_{T} - {\varvec{\upbeta }})^{'} {\mathbf{R}}^{'} _{1} \tilde{\Upsilon }_{1} \left\{ {\tilde{\Upsilon }_{1} {\mathbf{R}}_{1} s_{T} ^{2} ({\mathbf{X}}^{{\mathbf{'}}} {\mathbf{X}})^{{ - 1}} {\mathbf{R}}^{'} _{1} \tilde{\Upsilon }_{1} } \right\}^{{ - 1}} \tilde{\Upsilon }_{1} {\mathbf{R}}_{1} ({\mathbf{b}}_{T} - {\varvec{\upbeta }}) \\ = & \,\left[ {{\mathbf{R}}_{1} \left[ {\Upsilon _{1}^{{ - 1}} ({\mathbf{X^{\prime}X}})\Upsilon _{1}^{{ - 1}} } \right]^{{ - 1}} \Upsilon _{1}^{{ - 1}} {{\mathbf{X}}^{\prime}{\varvec{\upvarepsilon}}}} \right]^{\prime} \left\{ {s_{T}^{2} {\mathbf{R}}_{1} \left[ {\Upsilon _{1}^{{ - 1}} ({\mathbf{X^{\prime}X}})\Upsilon _{1}^{{ - 1}} } \right]^{{ - 1}} {\mathbf{R^{\prime}}}_{1} } \right\}^{{ - 1}} {\mathbf{R}}_{1} \left[ {\Upsilon _{1}^{{ - 1}} ({\mathbf{X^{\prime}X}})\Upsilon _{1}^{{ - 1}} } \right]^{{ - 1}} \Upsilon _{1}^{{ - 1}}{\mathbf{X}}^{\prime}{\varvec{\upvarepsilon}}\\ & \quad \xrightarrow{p}{\mathbf{z}}^{\prime } \left[ {\sigma ^{2} {\mathbf{R}}_{1} {\mathbf{Q}}_{1}^{{ - 1}} {\mathbf{R^{\prime}}}_{1} } \right]^{{ - 1}} {\mathbf{z}}, \\ \end{aligned} $$

(18)

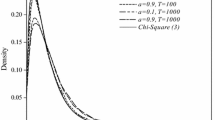
where $s_{T}^{2}$ is the sample estimate of σ², and ${\mathbf{R}}_{1} \varUpsilon_{1} ({\mathbf{b}}_{T} - {\varvec{\upbeta}}) \equiv {\mathbf{z}} \Rightarrow N(0,\;\sigma^{2} {\mathbf{R}}_{1} {\mathbf{Q}}_{1}^{ - 1} {\mathbf{R^{\prime}}}_{1} ).$ Therefore, W ⇒ χ²(3).