Shrinkage for covariance estimation: asymptotics, confidence intervals, bounds and applications in sensor monitoring and finance

Abstract

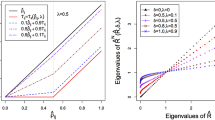
When shrinking a covariance matrix towards (a multiple) of the identity matrix, the trace of the covariance matrix arises naturally as the optimal scaling factor for the identity target. The trace also appears in other context, for example when measuring the size of a matrix or the amount of uncertainty. Of particular interest is the case when the dimension of the covariance matrix is large. Then the problem arises that the sample covariance matrix is singular if the dimension is larger than the sample size. Another issue is that usually the estimation has to based on correlated time series data. We study the estimation of the trace functional allowing for a high-dimensional time series model, where the dimension is allowed to grow with the sample size—without any constraint. Based on a recent result, we investigate a confidence interval for the trace, which also allows us to propose lower and upper bounds for the shrinkage covariance estimator as well as bounds for the variance of projections. In addition, we provide a novel result dealing with shrinkage towards a diagonal target. We investigate the accuracy of the confidence interval by a simulation study, which indicates good performance, and analyze three stock market data sets to illustrate the proposed bounds, where the dimension (number of stocks) ranges between 32 and 475. Especially, we apply the results to portfolio optimization and determine bounds for the risk associated to the variance-minimizing portfolio.

Appendix A: Proof of Theorem 4.2

We give a sketch of the proof. We apply Steland and von Sachs (2017b, Theorem 2.3), which generalizes Steland and von Sachs (2017a) and is based on techniques of Kouritzin (1995) and Philipp (1986). Steland and von Sachs (2017b, Theorem 2.3) is applied with $\varvec{v}_n^{(j)} = \varvec{w}_n^{(j)} = \varvec{e}_j$, where $\varvec{e}_j$ denotes the jth unit vector of the Euclidean space $\mathbb {R}^{d_n}$, $j = 1, \dots , d_n$ and $L_n = d_n$. Basically, the result asserts that, on a new probability space, one can approximate the partial sums

$$\begin{aligned} D_{nk}^{(j)} = \sum _{i=1}^k \varvec{v}_n^{(j)}{}' \varvec{Y}_{ni} \varvec{w}_n^{(j)}{}' \varvec{Y}_{ni}, \qquad j = 1, \dots , L_n, 1 \le k \le n, n \ge 1 \end{aligned}$$

by a Brownian motion, and here the number of such bilinear forms $L_n$ ($= d_n$ in our case) given by $L_n$ pairs of weighting vectors, may grow to $\infty$. Using the notation and definitions of Sect. 2.3 of Steland and von Sachs (2017b), we obtain

$$\begin{aligned} \mathcal {D}_{nj}(1)&= \frac{1}{\sqrt{n d_n}} D_{nn}^{(j)} ( \varvec{v}_n^{(j)}, \varvec{w}_n^{(j)} ) \\&= \frac{1}{\sqrt{n d_n}} \varvec{e}_j'( n \widehat{\varvec{\Sigma }}_n - {{\mathrm{\mathbb {E}}}}(n \widehat{\varvec{\Sigma }}_n) ) \varvec{e}_j \\&= \sqrt{n/d_n} \left( s_{nj}^2 - \sigma ^2_j \right) _{j=1}^{d_n}. \end{aligned}$$

By Steland and von Sachs (2017b, Theorem 2.3) we may redefine the above processes, on a new probability space together with a Gaussian random vector $\varvec{B}_n = (B_{n1}, \dots , B_{nd_n} )'$ with ${{\mathrm{\mathbb {E}}}}( \varvec{B}_n ) = 0$ and covariances given by

$$\begin{aligned} {{\mathrm{\mathbb Cov}}}( B_{n\nu }, B_{n\mu } ) = d_n^{-1} \widetilde{\beta }_n^2( \nu , \mu ), \end{aligned}$$

where $\widetilde{\beta }_n^2( \nu , \mu )$ satisfy

$$\begin{aligned} d_n^{-1} |\widetilde{\beta }_n^2( \nu , \mu ) - \beta _n^2( \nu , \mu ) | = o(1), \end{aligned}$$

by Lemma 2.1 and Theorem 2.2 of Steland and von Sachs (2017b) (there the quantities $\widetilde{\beta }_n^2( \nu , \mu )$ are denoted by $\beta _n^2( \nu , \mu )$), such that the strong approximation

$$\begin{aligned} \sum _{j=1}^{d_n} \left| \mathcal {D}_{nj} - B_j \right| ^2 = o(1), \end{aligned}$$

as $n \rightarrow \infty$, a.s., holds true. But this immediately yields

$$\begin{aligned} \left\| \bigl ( \sqrt{n/d_n} ( s_{nj}^2 - \sigma ^2_j ) \bigr )_{j=1}^{d_n} - \varvec{B}_n \right\| _2 = o(1), \end{aligned}$$

as $n \rightarrow \infty$, a.s. Now both assertions follow, because

$$\begin{aligned} \left\| \sqrt{n/d_n} ( \widehat{\varvec{D}}_n - \text {diag}^2( \varvec{\Sigma }_n ) ) - \text {diag}( \varvec{B}_n ) \right\| _2 = \left\| \bigl ( \sqrt{n/d_n} ( s_{nj}^2 - \sigma ^2_j ) \bigr )_{j=1}^{d_n} - \varvec{B}_n \right\| _2. \end{aligned}$$

$\square$