Efficient parameter estimation and variable selection in partial linear varying coefficient quantile regression model with longitudinal data

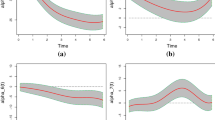
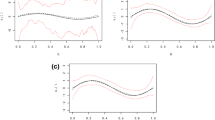
Abstract

Efficient estimation and variable selection in partial linear varying coefficient quantile regression model with longitudinal data is concerned in this paper. To improve estimation efficiency in quantile regression, based on B-spline basis approximation for nonparametric parts, we propose a new estimating function, which can incorporate the correlation structure between repeated measures. In order to reduce computational burdens, the induced smoothing method is used. The new method is empirically shown to be much more efficient and robust than the popular generalized estimating equations based methods. Under mild conditions, the asymptotically normal distribution of the estimators for the parametric components and the optimal convergence rate of the estimators for the nonparametric functions are established. Furthermore, to do variable selection, a smooth-threshold estimating equation is proposed, which can use the correlation structure and select the nonparametric and parametric parts simultaneously. Theoretically, the variable selection procedure works beautifully, including consistency in variable selection and oracle property in estimation. Simulation studies and real data analysis are included to show the finite sample performance.

Appendix

Proof of Theorem 2.1. Let $\bar{\varvec{U}}_{\tau }^o(\varvec{\zeta })=-\sum _{i=1}^n\varvec{D}_{i}^T \varvec{\Lambda }_i\varvec{R}_i^{-1} \varvec{P}_i(\varvec{\zeta })$ with $\varvec{P}_i(\varvec{\zeta })=\left( \tau -\Pr (y_{i1}-\varvec{d}_{i1}^T \varvec{\zeta }<0),\ldots ,\tau -\Pr (y_{im_i}-\varvec{d}_{im_i}^T \varvec{\zeta }<0)\right) ^T$. Then we can get that

$$\begin{aligned}&\frac{1}{n}\left[ \bar{\varvec{U}}_{\tau }^o(\varvec{\zeta }) -{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right] \\&\quad =\frac{1}{n}\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\left[ \varvec{S}_i(\varvec{\zeta })-\varvec{P}_i(\varvec{\zeta })\right] \\&\quad =\frac{1}{n}\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\begin{bmatrix} \Pr (y_{i1}-\varvec{d}_{i1}^T\varvec{\zeta }<0)-I(y_{i1} -\varvec{d}_{i1}^T\varvec{\zeta }<0) \\ \vdots \\ \Pr (y_{im_i}-\varvec{d}_{im_i}^T\varvec{\zeta }<0)-I(y_{im_i} -\varvec{d}_{im_i}^T\varvec{\zeta }<0) \end{bmatrix}\\&\quad =\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{m_i} \varvec{a}_{ij}\left[ \Pr (y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0) -I(y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0) \right] , \end{aligned}$$

where $\varvec{a}_{ij}$ is a $(p(K_{n}+\hbar +1)+q)\times 1$ vector with $\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}=(\varvec{a}_{i1},\ldots ,\varvec{a}_{im_i})$. Under condition (C4) and from the law of large numbers (Pollard 1990), we have that

$$\begin{aligned} \sup _{\varvec{\zeta }}\left| \frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{m_i}\varvec{a}_{ij}\left[ \Pr (y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0)-I(y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0)\right] \right| =o\left( \frac{1}{\sqrt{n}}\right) .\qquad \end{aligned}$$

(6.1)

Therefore, $\sup _{\varvec{\zeta }}\left\| \frac{1}{n} \left[ \bar{\varvec{U}}_{\tau }^o(\varvec{\zeta })-{\varvec{U}}_{\tau }^{o} (\varvec{\zeta })\right] \right\| =o\left( \frac{1}{\sqrt{n}}\right)$. By condition (C3), we know that $\varvec{\zeta }_0$ is the solution of $\bar{\varvec{U}}_{\tau }^o(\varvec{\zeta })=\varvec{0}$. Due to $\tilde{\varvec{\zeta }}^o$ is the solution of the equation ${\varvec{U}}_{\tau }^o(\varvec{\zeta })=\varvec{0}$ together with condition (C4), hence $\tilde{\varvec{\zeta }}^o\rightarrow _{p}\varvec{\zeta }_0$ as $n\rightarrow \infty$. For any $\varvec{\zeta }$ satisfying $\Vert \varvec{\zeta }-\varvec{\zeta }_0\Vert =O(n^{-1/3})$,

$$\begin{aligned}&{\varvec{U}}_{\tau }^o(\varvec{\zeta })-{\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)\\&\quad =-\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\left[ \varvec{S}_i(\varvec{\zeta })-\varvec{S}_i(\varvec{\zeta }_0)\right] \\&\quad =-\left\{ \sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{P}_i(\varvec{\zeta })+\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\left[ \varvec{S}_i(\varvec{\zeta })-\varvec{S}_i(\varvec{\zeta }_0)-\varvec{P}_i(\varvec{\zeta })\right] \right\} \\&\quad =-\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{P}_i(\varvec{\zeta })-\sum _{i=1}^n\sum _{j=1}^{m_i}\varvec{a}_{ij}\left[ \Pr (y_{ij} -\varvec{d}_{ij}^T\varvec{\zeta }<0)-I(y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0)\right. \\&\qquad +\left. I(y_{ij}-\varvec{d}_{ij}^T\varvec{\zeta }<0)-\tau \right] . \end{aligned}$$

According to Lemma 3 of Jung (1996), we have that

(6.2)

Therefore, ${\varvec{U}}_{\tau }^o(\varvec{\zeta })-{\varvec{U}}_{\tau }^o(\varvec{\zeta }_0) =\bar{\varvec{U}}_{\tau }^o(\varvec{\zeta })+o_{p}(\sqrt{n})$. By Taylor’s expansion of $\bar{\varvec{U}}_{\tau }^o(\varvec{\zeta })$ together with $\bar{\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)=\varvec{0}$, we can obtain

$$\begin{aligned} {\varvec{U}}_{\tau }^o(\varvec{\zeta })-{\varvec{U}}_{\tau }^o (\varvec{\zeta }_0)={\varvec{D}}_{\tau }(\varvec{\zeta }_0)(\varvec{\zeta } -\varvec{\zeta }_0)+o_{p}(\sqrt{n}), \end{aligned}$$

(6.3)

where

$$\begin{aligned} {\varvec{D}}_{\tau }(\varvec{\zeta }_0)=\frac{\partial \bar{{\varvec{U}}}_{\tau }^o(\varvec{\zeta })}{\partial \varvec{\zeta }}|_{\varvec{\zeta }=\varvec{\zeta }_0}=\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{\Lambda }_i\varvec{D}_{i}. \end{aligned}$$

Note that $\tilde{\varvec{\zeta }}^o$ is in the $n^{-1/3}$ neighborhood of $\varvec{\zeta }_0$ and ${\varvec{U}}_{\tau }^o(\tilde{\varvec{\zeta }}^o)=\varvec{0}$, we have

$$\begin{aligned} \tilde{\varvec{\zeta }}^o-\varvec{\zeta }_0=-{\varvec{D}}_{\tau }^{-1}(\varvec{\zeta }_0){\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)+o_{p}(\sqrt{n}). \end{aligned}$$

(6.4)

To obtain the closed form expression of $\tilde{\varvec{\beta }}^o$, similar to Ma et al. (2013), we write the inverse of ${\varvec{D}}_{\tau }(\varvec{\zeta }_0)$ as the following block form

$$\begin{aligned} {\varvec{D}}_{\tau }^{-1}(\varvec{\zeta }_0)= & {} \begin{bmatrix} \sum _{i=1}^n\varvec{X}_i^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{\Lambda }_i\varvec{X}_i&\quad \sum _{i=1}^n\varvec{X}_i^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{\Lambda }_i\varvec{\Pi }_{i}\\ \sum _{i=1}^n\varvec{\Pi }_{i}^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{\Lambda }_i\varvec{X}_i&\quad \sum _{i=1}^n\varvec{\Pi }_{i}^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{\Lambda }_i \varvec{\Pi }_{i} \end{bmatrix}^{-1} \\= & {} \begin{bmatrix} \varvec{D}_{\varvec{X}\varvec{X}}&\quad \varvec{D}_{\varvec{X}\varvec{\Pi }} \\ \varvec{D}_{\varvec{\Pi }\varvec{X}}&\quad \varvec{D}_{\varvec{\Pi }\varvec{\Pi }} \end{bmatrix}^{-1}=\begin{bmatrix} \varvec{D}^{11}&\quad \varvec{D}^{12} \\ \varvec{D}^{21}&\quad \varvec{D}^{22} \end{bmatrix}, \end{aligned}$$

where $\varvec{D}^{11}=\left( \varvec{D}_{\varvec{X}\varvec{X}}-\varvec{D}_{\varvec{X} \varvec{\Pi }}\varvec{D}^{-1}_{\varvec{\Pi }\varvec{\Pi }}\varvec{D}_{\varvec{\Pi }\varvec{X}}\right) ^{-1}$, $\varvec{D}^{22}=\left( \varvec{D}_{\varvec{\Pi }\varvec{\Pi }} -\varvec{D}_{\varvec{\Pi }\varvec{X}}\varvec{D}^{-1}_{\varvec{X}\varvec{X}}\varvec{D}_{\varvec{X} \varvec{\Pi }}\right) ^{-1}$, $\varvec{D}^{12}=-\varvec{D}^{11}\varvec{D}_{\varvec{X}\varvec{\Pi }} \varvec{D}_{\varvec{\Pi }\varvec{\Pi }}^{-1}$ and $\varvec{D}^{21}=-\varvec{D}^{22}\varvec{D}_{\varvec{\Pi } \varvec{X}}\varvec{D}_{\varvec{X}\varvec{X}}^{-1}$. Furthermore, let

$$\begin{aligned} {\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)= & {} ({\varvec{U}}_{\tau }^{o,1}(\varvec{\zeta }_0)^T,{\varvec{U}}_{\tau }^{o,2}(\varvec{\zeta }_0)^T)^T, \\ {\varvec{U}}_{\tau }^{o,1}(\varvec{\zeta }_0)= & {} -\sum _{i=1}^n\varvec{X}_i^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0), \\ {\varvec{U}}_{\tau }^{o,2}(\varvec{\zeta }_0)= & {} -\sum _{i=1}^n\varvec{\Pi }_i^T\varvec{\Lambda }_i\varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0). \end{aligned}$$

Then

$$\begin{aligned} \tilde{\varvec{\beta }}^o-\varvec{\beta }_0= & {} -\left[ \varvec{D}^{11} {\varvec{U}}_{\tau }^{o,1}(\varvec{\zeta }_0)+\varvec{D}^{12}{\varvec{U}}_{\tau }^{o,2} (\varvec{\zeta }_0)\right] +o_{p}\left( \frac{1}{\sqrt{n}}\right) \\= & {} \varvec{D}^{11}\sum _{i=1}^n\left[ \varvec{X}_i -\varvec{\Pi }_{i}\varvec{D}_{\varvec{\Pi }\varvec{\Pi }}^{-1}\varvec{D}_{\varvec{\Pi } \varvec{X}}\right] ^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0)+o_{p}\left( \frac{1}{\sqrt{n}}\right) . \end{aligned}$$

Thus,

$$\begin{aligned} \sqrt{n}(\tilde{\varvec{\beta }}^o-\varvec{\beta }_0) =(n\varvec{D}^{11})\frac{1}{\sqrt{n}}\sum _{i=1}^n\left[ \varvec{X}_i-\varvec{\Pi }_{i} \varvec{D}_{\varvec{\Pi }\varvec{\Pi }}^{-1}\varvec{D}_{\varvec{\Pi }\varvec{X}}\right] ^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0)+o_{p}\left( 1\right) . \end{aligned}$$

Because $\varvec{S}_i(\varvec{\zeta }_0)$ are independent random variables with mean zero, and

$$\begin{aligned} \text{ var }\left( \frac{1}{\sqrt{n}}\sum _{i=1}^n\left[ \varvec{X}_i-\varvec{\Pi }_{i} \varvec{D}_{\varvec{\Pi }\varvec{\Pi }}^{-1}\varvec{D}_{\varvec{\Pi }\varvec{X}}\right] ^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0)\right) =\varvec{\Xi }. \end{aligned}$$

The multivariate central limit theorem implies that

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{i=1}^n\left[ \varvec{X}_i-\varvec{\Pi }_{i} \varvec{D}_{\varvec{\Pi }\varvec{\Pi }}^{-1}\varvec{D}_{\varvec{\Pi }\varvec{X}}\right] ^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{S}_i(\varvec{\zeta }_0)\rightarrow _{d} N(\varvec{0},\varvec{\Xi }), \end{aligned}$$

furthermore,

$$\begin{aligned} n\varvec{D}^{11}=\left[ \frac{1}{n}\left( \varvec{D}_{\varvec{X} \varvec{X}}-\varvec{D}_{\varvec{X}\varvec{\Pi }}\varvec{D}_{\varvec{X} \varvec{\Pi }}^{-1}\varvec{D}_{\varvec{\Pi }\varvec{X}}\right) \right] ^{-1} \rightarrow _{p}\varvec{\Sigma }, \end{aligned}$$

by the law of large numbers. Then, by using Slutskys theorem, it follows that $\sqrt{n}(\tilde{\varvec{\beta }}^o-\varvec{\beta }_0)\rightarrow _{d} N(\varvec{0}, \varvec{\Sigma }^{-1}\varvec{\Xi }\varvec{\Sigma }^{-1})$. This complete the proof of part (a). Furthermore, by using the same arguments of proving the part (a), we can get

$$\begin{aligned} \frac{1}{n}\sum _{l=1}^p\sum _{i=1}^n\sum _{j=1}^{m_i} \left[ \varvec{\Pi }_{ij}^T\left( \hat{\varvec{\theta }}_l -\varvec{\theta }_{0l}\right) \right] = O_{p}\left( \frac{K_n}{n}\right) . \end{aligned}$$

The triangular inequality implies that

$$\begin{aligned}&\frac{1}{n}\sum _{l=1}^p\sum _{i=1}^n\sum _{j=1}^{m_i}(\tilde{\alpha }_{l}^o(t_{ij})-\alpha _{0l}(t_{ij}))^2\\&\quad \le \frac{2}{n}\sum _{l=1}^p\sum _{i=1}^n\sum _{j=1}^{m_i}\left[ \varvec{\Pi }_{ij}^T\left( \hat{\varvec{\theta }}_l-\varvec{\theta }_{0l}\right) \right] ^2+ \frac{2}{n}\sum _{l=1}^p\sum _{i=1}^n\sum _{j=1}^{m_i}\left[ \varvec{\Pi }_{ij}^T\varvec{\theta }_{0l}-\alpha _{0l}(t_{ij})\right] ^2\\&\quad =O_{p}\left( \frac{K_n}{n}+K_n^{-2r}\right) . \end{aligned}$$

The proof is completed.

Proof of Theorem 2.2

$$\begin{aligned} \varvec{\varsigma }\left( \varvec{\zeta }\right) =\left( \begin{aligned}&\varvec{\Xi }^{-1/2}\varvec{\Sigma }(\varvec{\beta }-\varvec{\beta }_{0}) \\&K_{n}^{-1/2}\varvec{H}_{n}(\varvec{\Theta }-\varvec{\Theta }_0) +K_{n}^{1/2}\varvec{H}_{n}^{-1}\varvec{\Pi }^T\varvec{\Lambda } \varvec{Z}(\varvec{\beta }-\varvec{\beta }_{0}) \end{aligned} \right) , \end{aligned}$$

(6.5)

where $\varvec{H}_{n}^2=K_{n}\varvec{\Pi }^T\varvec{\Lambda }\varvec{\Pi }$. Furthermore, we standardize $\widetilde{\varvec{z}}_{ij}=\varvec{\Xi }^{1/2}\varvec{\Sigma }^{-1}\varvec{z}_{ij}$ and $\widetilde{\varvec{\Pi }}_{ij}=K_{n}^{1/2}\varvec{H}_{n}^{-1}\varvec{\Pi }_{ij}$. Note that $\tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }}) =I(-\Delta _{ij})\Phi (-|\Delta _{ij}|)$, where $\Delta _{ij}=(\epsilon _{ij}+u_{ij})/r_{ij}$ with $u_{ij}=-(\varvec{\varsigma }\left( \varvec{\zeta }\right) ^T (\widetilde{\varvec{z}}_{ij}^T,\widetilde{\varvec{\Pi }}_{ij}^T)^T+R_{nij})$ and $R_{nij}=\varvec{\Pi }_{ij}^T\varvec{\Theta }_0-\sum _{l=1}^px_{ij}^l \alpha _{0l}(t_{ij})$. We can obtain

$$\begin{aligned} \frac{1}{\sqrt{n}}\left[ {\varvec{U}}_{\tau }^o(\varvec{\zeta }) -\tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right]= & {} \frac{1}{\sqrt{n}} \sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\begin{bmatrix} I(-\Delta _{i1})\Phi (-|\Delta _{i1}|) \\ \vdots \\ I(-\Delta _{im_i})\Phi (-|\Delta _{im_i}|) \end{bmatrix}\\= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^n \sum _{j=1}^{m_i}\varvec{a}_{ij}I(-\Delta _{ij})\Phi (-|\Delta _{ij}|). \end{aligned}$$

Note that

$$\begin{aligned}&E\left( \tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right) \\&\quad =\int _{-\infty }^{\infty }I(-\Delta _{ij})\Phi (-|\Delta _{ij}|)f_{ij}(\epsilon )d\epsilon \\&\quad =\int _{-\infty }^{\infty }\Phi (-|\epsilon _{ij}+u_{ij}|/r_{ij})\{2I(\epsilon _{ij}+u_{ij}<0)-1\}f_{ij}(\epsilon )d\epsilon \\&\quad =r_{ij}\int _{-\infty }^{\infty }\Phi (-|t|)\{2I(t<0)-1\}\left[ f_{ij}(0)+f_{ij}^T(\eta (t))(r_{ij}t-u_{ij})\right] dt, \end{aligned}$$

where $\eta (t)$ is between 0 and $r_{ij}t-u_{ij}$. Because $\int _{-\infty }^{\infty }\Phi (-|t|)\{2I(t<0)-1\}dt=0$, and by condition (C3), there exists a constant C such that $\sup _{i,j}|f_{ij}^T(\eta (t))|\le C$. Then note that $\int _{-\infty }^{\infty }\Phi (-|t|)|t|dt=1/2$, we have that

$$\begin{aligned} \left| E\left( \tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right) \right| \le r_{ij}^2\int _{-\infty }^{\infty }\Phi (-|t|)|t||f_{ij}^T(\eta (t))|dt\le \frac{Cr_{ij}^2}{2}. \end{aligned}$$

Under conditions (C4) and (C5), as $n\rightarrow \infty$, we can obtain

$$\begin{aligned} \left\| \frac{1}{\sqrt{n}}\left[ {\varvec{U}}_{\tau }^o (\varvec{\zeta })-\tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right] \right\| =\frac{1}{\sqrt{n}}\sup _{ij}\Vert \varvec{a}_{ij}\Vert \sum _{i=1}^n\frac{Cr_{ij}^2}{2}=o(1). \end{aligned}$$

In addition, by Cauchy–Schwartz inequality,

$$\begin{aligned}&\frac{1}{{n}}\text{ var }\left[ {\varvec{U}}_{\tau }^o(\varvec{\zeta })-\tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right] \\&\quad =\frac{1}{{n}}\sum _{i=1}^n\text{ var }\left[ \sum _{j=1}^{m_i}\varvec{a}_{ij}I(-\Delta _{ij})\Phi (-|\Delta _{ij}|)\right] \\&\quad \le \frac{1}{{n}}\sum _{i=1}^n\sum _{j=1}^{m_i}\varvec{a}_{ij}^T\varvec{a}_{ij}\text{ var }\left[ \tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right] \\&\qquad +\, \frac{1}{{n}}\sum _{i=1}^n\sum _{j=1}^{m_i}\sum _{j^*=1,j^*\ne j}^{m_i}\varvec{a}_{ij}^T\varvec{a}_{ij^*}\left\{ \text{ var }\left[ \tilde{{S}}_{ij} ({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right] \text{ var }\left[ \tilde{{S}}_{ij^*} ({\varvec{\zeta }})-{{S}}_{ij^*}({\varvec{\zeta }})\right] \right\} ^{1/2}. \end{aligned}$$

For $j=1,\ldots ,m_i$,

$$\begin{aligned} \text{ var }\left[ \tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right]\le & {} E\left[ \tilde{{S}}_{ij}({\varvec{\zeta }})-{{S}}_{ij}({\varvec{\zeta }})\right] ^2 \\= & {} \int _{-\infty }^{\infty }\left\{ I(-\Delta _{ij})\Phi (-|\Delta _{ij}|)\right\} ^2f_{ij}(\epsilon )d\epsilon \\= & {} r_{ij}\int _{-\infty }^{\infty }\Phi ^2(-|t|)f_{ij}(r_{ij}t-u_{ij})dt \\= & {} r_{ij}\int _{|t|>c}\Phi ^2(-|t|)f_{ij}(r_{ij}t-u_{ij})dt \\&+\, r_{ij}\int _{|t|\le c}\Phi ^2(-|t|)f_{ij}(r_{ij}t-u_{ij})dt \\\le & {} \Phi ^2(-c)+r_{ij}cf_{ij}(\eta ), \end{aligned}$$

where $\eta$ is a positive value, and $\eta$ lies between $(-r_{ij}c-u_{ij},r_{ij}c-u_{ij})$. Let $c=n^{1/3}$, under condition (C5), since $r_{ij}=O(n^{-1/2})$, then $r_{ij}c=O(n^{-1/6})$. Note that $\Phi ^2(-c)\rightarrow 0$ and $r_{ij}cf_{ij}(\eta )\rightarrow 0$, as $n\rightarrow \infty$. By conditions (C4) and (C6), it is easy to obtain $\frac{1}{{n}}\text{ var }\left[ {\varvec{U}}_{\tau }^o (\varvec{\zeta })-\tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right] =o(1)$. Therefore, we have $\frac{1}{\sqrt{n}}\left[ {\varvec{U}}_{\tau }^o (\varvec{\zeta })-\tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right] \rightarrow 0$ as $n\rightarrow \infty$ for any $\varvec{\zeta }$. The proof is completed.

Proof of Theorem 2.3

Note that $\sup _{\varvec{\zeta }}\Vert \frac{1}{n}\left( \bar{{\varvec{U}}}_{\tau }^o (\varvec{\zeta })-{\varvec{U}}_{\tau }^o(\varvec{\zeta })\right) \Vert =o \left( \frac{1}{\sqrt{n}}\right)$, and by Theorem 2.2, we know that $\sup _{\varvec{\zeta }}\Vert \frac{1}{n}\left( \bar{{\varvec{U}}}_{\tau }^o (\varvec{\zeta })-\tilde{{\varvec{U}}}_{\tau }^o(\varvec{\zeta })\right) \Vert =o \left( \frac{1}{\sqrt{n}}\right)$. Because that $\varvec{\zeta }_0$ is the unique solution of equation of $\bar{{\varvec{U}}}_{\tau }^o(\varvec{\zeta })=\varvec{0}$. This together with the definition of $\tilde{\varvec{\zeta }}$ implies that $\tilde{\varvec{\zeta }}\rightarrow _{p}\varvec{\zeta }_0$ as $n\rightarrow \infty$. In order to prove the asymptotic normality of $\tilde{\varvec{\zeta }}$, we first prove that $\frac{1}{n}\{\tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0) -{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\}\rightarrow _{p} 0$. Note that $E\left[ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right] -{\varvec{D}}_{\tau }(\varvec{\zeta }_0)=(D_{ij})_{i,j=1,\ldots ,n}$, with $D_{ij}=\frac{1}{r_{ij}}E\phi \left( \frac{\epsilon _{ij} +u_{ij}}{r_{ij}}\right) -f_{ij}(0)$. Because that

$$\begin{aligned}&\left| \frac{1}{r_{ij}}E\phi \left( \frac{\epsilon _{ij}+u_{ij}}{r_{ij}}\right) -f_{ij}(0)\right| \\&\quad =\left| \frac{1}{r_{ij}}\int _{-\infty }^{+\infty }\phi \left( \frac{\epsilon +u_{ij}}{r_{ij}}\right) f_{ij}(\epsilon )d\epsilon -f_{ij}(0)\right| \\&\quad =\left| \int _{-\infty }^{+\infty }\phi (t)\left\{ f_{ij}(0)+(r_{ij}t-u_{ij})f_{ij}^T(\eta (t))\right\} dt-f_{ij}(0)\right| \\&\quad =\left| \int _{-\infty }^{+\infty }\phi (t)(r_{ij}t-u_{ij})f_{ij}^T(\eta (t))dt\right| \\&\quad \le r_{ij}\int _{-\infty }^{+\infty }\left| \phi (t)tf_{ij}^T(\eta (t))\right| dt+\int _{-\infty }^{+\infty }\left| \phi (t)u_{ij}f_{ij}^T(\eta (t))\right| dt, \end{aligned}$$

where $\eta (t)$ lies between 0 and $r_{ij}t-u_{ij}$. By condition (C3), $f_{ij}^T(\cdot )$ is uniformly bounded, hence there exists a constant C satisfying $|f_{ij}^T(\eta (t))|\le C$, and by condition (C5), we have $|\frac{1}{r_{ij}}E\phi (\frac{\epsilon _{ij}+u_{ij}}{r_{ij}})-f_{ij}(0)|\rightarrow 0$. By the strong law of large number, we know that $\frac{1}{n}\tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\rightarrow E[\frac{1}{n}\tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)]$. Using the triangle inequality, we have

$$\begin{aligned}&\left| \frac{1}{n}\left\{ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)-{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right\} \right| \\&\quad \le \left| \frac{1}{n}\left\{ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)-E\left[ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right] \right\} \right| + \left| \frac{1}{n}\left\{ E\left[ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right] -{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right\} \right| \\&\quad =o(1), \end{aligned}$$

which implies that $\frac{1}{n}\left\{ \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0) -{\varvec{D}}_{\tau }(\varvec{\zeta }_0)\right\} \rightarrow _{p}0$. By Taylor series expansion of $\tilde{{\varvec{U}}}_{\tau }^o(\varvec{\zeta })$ around $\varvec{\zeta }_0$, we have $\tilde{{\varvec{U}}}_{\tau }^o(\varvec{\zeta })=\tilde{{\varvec{U}}}_{\tau }^o (\varvec{\zeta }_0)+\tilde{\varvec{D}}_{\tau }(\varvec{\zeta }^*)(\varvec{\zeta }-\varvec{\zeta }_0)$, where $\varvec{\zeta }^*$ lies between $\varvec{\zeta }$ and $\varvec{\zeta }_0$. Because $\tilde{{\varvec{U}}}_{\tau }^o(\tilde{\varvec{\zeta }})=\varvec{0}$ and $\tilde{\varvec{\zeta }}\rightarrow \varvec{\zeta }_0$, we therefore obtain $\varvec{\zeta }^*\rightarrow \varvec{\zeta }_0$ and $\tilde{\varvec{D}}_{\tau }(\varvec{\zeta }^*)\rightarrow \tilde{\varvec{D}}_{\tau }(\varvec{\zeta }_0)$. Then by the same arguments used in the proof of Theorem 2.2, we can complete the proof of Theorem 2.3.

Proof (a) of Theorem 3.2. Let $\delta _n=n^{-r/(2r+1)}$, $\varvec{\beta }=\varvec{\beta }_0+\delta _n\varvec{T}_1$, $\varvec{\Theta }=\varvec{\Theta }_0+\delta _n\varvec{T}_2$ and $\varvec{T}=(\varvec{T}_1^T,\varvec{T}_2^T)^T$. Let $\varvec{S}_n(\varvec{\beta },\varvec{\Theta })=\left( \varvec{I}_{p(K_{n}+\hbar +1)+q}-\hat{\varvec{\Psi }}\right) \tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta })+\hat{\varvec{\Psi }}\varvec{\zeta }$. Our aim is to show that for $\varepsilon >0$, there exists a constant $C>0$, such that

$$\begin{aligned} \Pr \left( \sup _{\Vert \varvec{T}\Vert =C}\delta _n\varvec{T}^{T} \varvec{S}_n(\varvec{\beta }_0+\varvec{T}_1,\varvec{\Theta }_0+\varvec{T}_2)>0\right) \ge 1-\varepsilon , \end{aligned}$$

for n large enough. This will imply with probability at least $1-\varepsilon$ that there exists a local minimum value of the equation $\varvec{S}_n(\varvec{\beta },\varvec{\Theta })=\varvec{0}$ such that $\Vert \left( \hat{\varvec{\beta }}^T,\hat{\varvec{\Theta }}^T\right) ^T -\left( \varvec{\beta }_0^T,\varvec{\Theta }_0^T\right) ^T\Vert =O_{p}(\delta _n)$. We will evaluate the sign of $\delta _n\varvec{T}^T\varvec{S}_n(\varvec{\beta }_0+\varvec{T}_1,\varvec{\Theta }_0+\varvec{T}_2)$ in the ball $\{\varvec{\beta }_0+\varvec{T}_1,\varvec{\Theta }_0+\varvec{T}_2:\Vert \varvec{T}\Vert =C\}$. By the Taylor approximation, we have that

$$\begin{aligned} \delta _n\varvec{T}^T\varvec{S}_n(\varvec{\beta }_0+\varvec{T}_1, \varvec{\Theta }_0+\varvec{T}_2)= & {} \delta _n\varvec{T}^T \varvec{S}_n(\varvec{\beta }_0,\varvec{\Theta }_0)+ \delta _n^2\varvec{T}^T \frac{\partial \varvec{S}_n(\tilde{\varvec{\beta }}, \tilde{\varvec{\Theta }})}{\partial \left( \varvec{\beta }^T, \varvec{\Theta }^T\right) ^T}\varvec{T}\nonumber \\= & {} I_{n1}+I_{n2}, \end{aligned}$$

(6.6)

where $(\tilde{\varvec{\beta }}^T,\tilde{\varvec{\Theta }}^T)^T$ lies between $\left( \varvec{\beta }_0^T,\varvec{\Theta }_0^T\right) ^T$ and $\left( \varvec{\beta }_0^T,\varvec{\Theta }_0^T\right) ^T+\delta _n\varvec{T}$. Next we will consider $I_{n1}$ and $I_{n2}$ respectively. For $I_{n1}$, by some elementary calculations, we have

$$\begin{aligned} I_{n1}= & {} \delta _n\varvec{T}^T\left( \varvec{I}_{p(K_{n}+\hbar +1)+q} -\hat{\varvec{\Psi }}\right) \tilde{\varvec{U}}_{\tau }^o (\varvec{\zeta }_0)+\delta _n\varvec{T}^T\hat{\varvec{\Psi }}\varvec{\zeta }_0\\= & {} I_{n11}+I_{n12}. \end{aligned}$$

By Cauchy–Schwarz inequality, we can derive that

$$\begin{aligned} |I_{n11}|\le & {} \delta _n\left\| \varvec{T}^T\left( \varvec{I}_{p(K_{n}+\hbar +1)+q}-\hat{\varvec{\Psi }}\right) \right\| \left\| \tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)\right\| \\\le & {} \delta _n\left( 1-\min \left[ \min \{\hat{\delta }_{1,k}:\hat{\delta }_{1,k}\ne 1\},\min \{\hat{\delta }_{2,k}:\hat{\delta }_{2,k}\ne 1 \}\right] \right) \Vert \varvec{T}\Vert \left\| \tilde{\varvec{U}}_{\tau }^o(\varvec{\zeta }_0)\right\| . \end{aligned}$$

Since $\min \{\hat{\delta }_{1,k}:\hat{\delta }_{1,k}\ne 1\} \le \min \{\hat{\delta }_{1,k}:k=1,\ldots ,v\}$ and $\min \{\hat{\delta }_{2,k}:\hat{\delta }_{2,k}\ne 1\}\le \min \{\hat{\delta }_{2,k}:k=1,\ldots ,c\}$. We only need to obtain the convergence rate of $\min \{\hat{\delta }_{1,k}:k=1,\ldots ,v\}$ and $\min \{\hat{\delta }_{2,k}:k=1,\ldots ,c\}$. By Theorem 2.3, we know that the initial estimator $(\tilde{\varvec{\beta }},\tilde{\varvec{\Theta }})$ satisfy $\Vert (\tilde{\varvec{\beta }},\tilde{\varvec{\Theta }})-(\varvec{\beta }_0,\varvec{\Theta }_0) \Vert =O_{p}(n^{-r/(2r+1)})$. By using the condition $n^{r/(2r+1)}\lambda _{\max }\rightarrow 0$, for any $\varepsilon >0$ and $k\in \{1,\ldots ,v\}$, we can derive that

$$\begin{aligned} \Pr \left( \hat{\delta }_{1,k}>n^{\frac{-r}{1+2r}}\varepsilon \right)= & {} \Pr \left( \frac{\lambda _{\max }}{|\tilde{\varvec{\theta }}_k|^{1+\tau }}>n^{\frac{-r}{1+2r}}\varepsilon \right) \\= & {} \Pr \left( (\lambda _{\max } n^{\frac{r}{1+2r}}/\varepsilon )^{1/(1+\tau )}>|\tilde{\varvec{\theta }}_k|\right) \\\le & {} \Pr \left( (\lambda _{\max } n^{\frac{r}{1+2r}}/\varepsilon )^{1/(1+\tau )} >\min _{k\in \{1,\ldots ,v\}}\Vert \tilde{\varvec{\theta }}_{0k}\Vert -O_{p}(n^{-r/(2r+1)})\right) \\&\rightarrow 0, \end{aligned}$$

which implies that for each $k\in \{1,\ldots ,v\}$, $\hat{\delta }_{1,k}=o_{p}(n^{-r/(2r+1)})$. Therefore, we can get that $\min _{k=1,\ldots ,v}\hat{\delta }_{1,k}=o_{p}(n^{-r/(2r+1)})$. Similarly, we can prove that $\hat{\delta }_{2,k}=o_{p}(n^{-r/(2r+1)})$, for each $k\in \{1,\ldots ,c\}$. Therefore, we have that

$$\begin{aligned} \min \left[ \min _{k\in \mathcal {A}_1}\hat{\delta }_{1,k},\min _{k\in \mathcal {A}_2}\hat{\delta }_{2,k}\right] =o_{p}(n^{-r/(2r+1)}). \end{aligned}$$

Thus, we can obtain that

$$\begin{aligned} |I_{n11}|=O_{p}(\sqrt{n}\delta _n)\Vert \varvec{T}\Vert -o_{p}(\sqrt{n} \delta _n^2)\Vert \varvec{T}\Vert . \end{aligned}$$

Furthermore, for the $I_{n12}$, we have $I_{n12}\le \delta _n\Vert \varvec{T}\Vert \Vert \varvec{\zeta }_0\Vert =O_{p}(\delta _n\Vert \varvec{T}\Vert )$. Therefore, $I_{n1}=O_{p}(\sqrt{n}\delta _n^2\Vert \varvec{T}\Vert )$. For $I_{n2}$, we can obtain that

$$\begin{aligned} I_{n2}= & {} \delta _n^2\varvec{T}^T\frac{\partial \varvec{S}_n(\tilde{\varvec{\beta }},\tilde{\varvec{\Theta }})}{\partial \left( \varvec{\beta }^T,\varvec{\Theta }^T\right) ^T}\varvec{T}\\= & {} n\delta _n^2\varvec{T}^T\left( \varvec{I}_{p(K_{n}+\hbar +1)+q}-\hat{\varvec{\Psi }}\right) \left\{ \frac{1}{\sqrt{n}}\sum _{i=1}^n\varvec{D}_{i}^T\varvec{\Lambda }_i \varvec{R}_i^{-1}\varvec{\Lambda }_i\varvec{D}_{i}\right\} \varvec{T}\\&+\,\delta _n^2\varvec{T}^T\hat{\varvec{\Psi }}\varvec{T}+o_{p}(n\delta _n^2)\\= & {} I_{n21}+I_{n22}+o_{p}(n\delta _n^2). \end{aligned}$$

With the same argument, it is easy to prove that $I_{n22}=O_{p}(\delta _n^2)\Vert \varvec{T}\Vert =o(n\delta _n^2\Vert \varvec{T}\Vert )$. Thus, $\delta _n\varvec{T}^T\varvec{S}_n(\varvec{\beta }_0+\varvec{T}_1,\varvec{\Theta }_0+\varvec{T}_2)$ is asymptotically dominated in probability by $I_{n21}$ on $\{\varvec{\beta }_0+\varvec{T}_1,\varvec{\Theta }_0+\varvec{T}_2:\Vert \varvec{T}\Vert =C\}$, which is positive for the sufficiently large C. This implies, with probability at least $1-\varepsilon$, that there exists a local minimizer $\left( \hat{\varvec{\beta }}^T,\hat{\varvec{\Theta }}^T\right) ^T$ such that $\Vert \left( \hat{\varvec{\beta }}^T,\hat{\varvec{\Theta }}^T\right) ^T -\left( \varvec{\beta }_0^T,\varvec{\Theta }_0^T\right) ^T\Vert =O_{p}(\delta _n)$. Then by the same arguments used in the proof of Theorem 2.1, the proof can be completed.

Proof of Theorem 3.1

For any given $k\in \{v+1,\ldots ,p\}$, we have $\Vert \tilde{\varvec{\theta }}_k\Vert =O_p(-r/(2r+1))$, together with $n^{(1+\tau )r/(2r+1)}\lambda _{\min }\rightarrow \infty$, we can derive that

$$\begin{aligned} \Pr \left( \frac{\lambda _2}{\Vert \tilde{\varvec{\theta }}_k\Vert ^{1+\tau }}<1\right)= & {} \Pr \left( \Vert \tilde{\varvec{\theta }}_k\Vert ^{1+\tau }>\lambda _2\right) \\\le & {} \frac{1}{\lambda _2}E\left( \Vert \tilde{\varvec{\theta }}_k\Vert ^{1+\tau }\right) \\= & {} \frac{1}{\lambda _2}n^{-(1+\tau )r/(2r+1)}\\\le & {} \frac{1}{\lambda _{\min }}n^{-(1+\tau )r/(2r+1)}\rightarrow 0, \end{aligned}$$

This implies that $\lim _{n\rightarrow \infty }\Pr \left( \hat{\delta }_{1,k}=1, \text{ for } \text{ all }~~k\in \{v+1,\ldots ,p\} \right) =1$. On the other hand, by the condition $n^{r/(2r+1)}\lambda _{\max }\rightarrow 0$, for $\varepsilon > 0$ and $k\in \{1,\ldots ,v\}$, we have that $\Pr \left( \hat{\delta }_{1,k}>n^{\frac{-r}{1+2r}}\varepsilon \right) \rightarrow 0$, which implies that for each $k\in \{1,\ldots ,v\}$, $\hat{\delta }_{1,k}=o_{p}(n^{-r/(2r+1)})$. Therefore, we can get that $\lim _{n\rightarrow \infty }\Pr \left( \hat{\delta }_{1,k}<1, \text{ for } \text{ all } k\in \{1,\ldots ,v\} \right) =1$. The proof of (a) is completed. For part (b), apply the similar techniques as in part (a), we have, with probability tending to 1, that $\hat{\delta }_{2,k}=1$ for $k\in \{c+1,\ldots ,q\}$ and $\hat{\delta }_{2,k}<1$ for $k\in \{1,\ldots ,c\}$.

Proof (b) of Theorem 3.2. It can be proved by using the same method used in the proof of Theorem 2.2 in Wang and Lin (2016), we omit the detail for saving space.