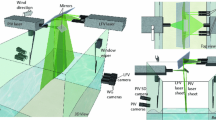
Abstract
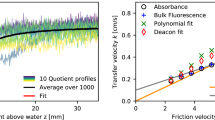
A method for observing near-surface fluctuations in pH caused by a water–air flux of carbon dioxide under conditions of ambient atmospheric carbon dioxide levels is developed and tested. Peaks in fluorescence intensity measured as a function of pH and turbulence are shown to be consistent with predictions from a chemical kinetics model of CO2 exchange. The square root of the frequency of the pH fluctuations scale linearly with independently measured bulk air–water gas transfer velocities in agreement with surface divergence models for air–water gas transfer. These data indicate that the method proposed here is tracking changes in near-surface CO2 concentrations. This laser-induced fluorescence method can be used to study the air–water exchange of CO2 in wind-wave tunnels without the need for elevated CO2 concentrations in the gas phase.










Similar content being viewed by others
References
Asher WE, Pankow JF (1986) The interaction of mechanically generated turbulence and interfacial films with a liquid phase controlled gas/liquid transport process. Tellus 38B:305–318
Asher WE, Pankow JF (1989) Direct observation of concentration fluctuations close to a gas/liquid interface. Chem Eng Sci 44:1451–1455
Asher WE, Pankow JF (1991) The effect of surface films on concentration fluctuations close to a gas/liquid interface. In: Wilhelms SE, Gulliver JS (eds) Air–water mass transfer. American Society of Civil Engineering, New York, pp 68–80
Asher WE, Karle LM, Higgins BJ, Farley PJ, Monahan EC, Leifer IS (1996) The influence of bubble plumes on air–seawater gas transfer velocities. J Geophys Res 101:12027–12041
Atmane MA, Asher WE, Jessup AT (2004) On the use of the active infrared technique to infer heat and gas transfer velocities at the air–water free surface. J Geophys Res 109. doi:10.1029/2003JC001805
Brumley BH, Jirka GH (1988) Air–water transfer of slightly soluble gases: turbulence, interfacial processes and conceptual models. PCH Physicochem Hydrodyn 10:295–319
Chu CR, Jirka GH (1992) Turbulent gas flux measurements below the air–water interface of a grid-stirred tank. Int J Heat Mass Transf 35:1957–1968
Csanady GT (1990) The role of breaking wavelets in air–sea gas transfer. J Geophys Res 95C:749–760
DOE (1994) Handbook of methods for the analysis of the various parameters of the carbon dioxide system in sea water; Version 2. In: Dickson AG, Goyet C (eds) Oak Ridge National Laboratory/Carbon Dioxide Information and Analysis Center Publication 74, pp 154
Garbe CS, Schimpf U, Jahne B (2004) A surface renewal model to analyze infrared images sequences of the ocean surface for the study of air–sea heat and gas exchange. J Geophys Res 109:C08S15. doi:10.1029/2003JC001802
Gibbons BH, Edsall JT (1963) Rate of hydration of carbon dioxide and dehydration of carbonic acid at 25 degrees. J Biol Chem 238:3502–3507
Hall G, Watt JM (1976) Modern numerical methods for ordinary differential equations. Clarendon Press, Oxford
Herlina, Jirka GH (2004) Application of LIF to investigate gas transfer near the air–water interface in a grid-stirred tank. Exp Fluids 37:341–349
Herlina, Jirka GH (2008) Experiments on gas transfer at the air–water interface induced by oscillating grid turbulence. J Fluid Mech 594:183–208
Hiby JW (1968) Fluorescence method for study of the transport mechanism of gas absorption by a falling film. Waerme Stoffuebertragung 1:105–116
Ho C, Sturtevant JM (1963) Kinetics of hydration of carbon dioxide at 25 degrees. J Biol Chem 238:3499–3502
Jähne B, Libner P, Fischer R, Billen T, Plate EJ (1989) Investigating the transfer process across the free aqueous viscous boundary layer by the controlled flux method. Tellus 41B:177–195
Karohl JG (1967) Peak detection logic systems of gas chromatographic integrators. J Gas Chromatogr 5:627–630
Komori S, Murakami Y, Ueda H (1989) The relationship between surface-renewal and bursting motions in an open-channel flow. J Fluid Mech 203:103–123
Lee YH, Luk S (1982) Characterization of concentration boundary layer in oxygen absorption. Ind Eng Chem Fund 21:428–434
Leonhardt H, Gordon L, Livingston R (1971) Acid–base equilibria of fluorescein and 2′,7′-dicholorfluorescein in their ground and fluorescent states. J Phys Chem 75:245–249
McKenna SP, McGillis WR (2004) The role of free-surface turbulence and surfactants in air–water gas transfer. Int J Heat Mass Transf 47:539–553. doi:10.1016/j.ijheatmasstransfer.2003.06.001
Mukto M, Atmane MA, Loewen MR (2007) A particle-image based wave profile measurement technique. Exp Fluids 42:131–142
Münsterer T, Jähne B (1998) LIF measurements of concentration profiles in the aqueous mass boundary layer. Exp Fluids 25:190–196
Pocker Y, Bjorkquist DW (1977) Stopped-flow studies of carbon dioxide hydration and bicarbonate dehydration in water and water-d2. Acid–base and metal ion catalysis. J Am Chem Soc 99:6537–6543
Schimpf U, Garbe CS, Jahne B (2004) Investigation of transport processes across the sea-surface microlayer by infrared imagery. J Geophys Res 109:C08S13. doi:10.1029/2003JC001803
Siddiqui MHK, Loewen MR, Asher WE, Jessup AT (2004) Coherent structures beneath wind waves and their influence on air–water gas transfer. J Geophys Res 109:C03024. doi:03010.01029/02002JC001559
Stumm W, Morgan JJ (1981) Aquatic chemistry, 2nd edn. Wiley-Interscience, New York
Takehara K, Etoh GT (2002) A direct visualization method of CO2 gas transfer at water surface driven by wind waves. In: Donelan M, Drennan WM, Saltzman ES, Wanninkhof R (eds) Gas transfer at water surfaces. American Geophysical Union, Washington, DC, pp 89–95
Tsumori H, Sugihara Y (2007) Lengthscales of motions that control air–water gas transfer in grid-stirred turbulence. J Mar Syst 66:6–18
Variano E, Bodenschatz E, Cowen EA (2004) A random synthetic jet array driven turbulence tank. Phys Fluids 37:613–615
Wolff LM, Hanratty TJ (1994) Instantaneous concentration profiles of oxygen accompanying absorption in a stratified flow. Exp Fluids 16:385–392
Woodrow PT Jr, Duke SR (2001) Laser-induced fluorescence studies of oxygen transfer across unsheared flat and wavy air–water interfaces. Ind Eng Chem Res 40:1985–1995
Acknowledgments
We wish to thank the three anonymous reviewers whose constructive criticisms of this manuscript paper were appreciated. This research was supported by the National Science Foundation under grant OCE-0425305.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Asher, W.E., Litchendorf, T.M. Visualizing near-surface concentration fluctuations using laser-induced fluorescence. Exp Fluids 46, 243–253 (2009). https://doi.org/10.1007/s00348-008-0554-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00348-008-0554-9