Piecewise Smooth Dynamical Systems Theory: The Case of the Missing Boundary Equilibrium Bifurcations

Abstract

We present two codimension-one bifurcations that occur when an equilibrium collides with a discontinuity in a piecewise smooth dynamical system. These simple cases appear to have escaped recent classifications. We present them here to highlight some of the powerful results from Filippov’s book Differential Equations with Discontinuous Righthand Sides (Kluwer, 1988). Filippov classified the so-called boundary equilibrium collisions without providing their unfolding. We show the complete unfolding here, for the first time, in the particularly interesting case of a node changing its stability as it collides with a discontinuity. We provide a prototypical model that can be used to generate all codimension-one boundary equilibrium collisions, and summarize the elements of Filippov’s work that are important in achieving a full classification.

1 Introduction

A piecewise smooth dynamical system (Filippov 1988; Bernardo et al. 2008) consists of a finite set of equations

$$\begin{aligned} \dot{x}=f^i(x), \quad x\in G_i\subset {\mathbb {R}}^n \end{aligned}$$

(1)

where the smooth vector fields $f^i$, defined on disjoint open regions $G_i$, are smoothly extendable to their closure $\overline{G}_i$, and assumed to depend on a parameter $\alpha \in {\mathbb {R}}$ (we will not write the dependence on $\alpha$ explicitly). The regions $G_i$ are separated by an $(n-1)$-dimensional hypersurface $\Sigma$ called the switching surface. The union of $\Sigma$ and all $G_i$ covers the whole state space $D \subseteq {\mathbb {R}}^n$.

What happens under typical conditions when an equilibrium of one of the smooth vector fields $f^i$ collides with $\Sigma$, as the parameter $\alpha$ is varied? This is an elementary problem of piecewise smooth dynamical systems theory, termed a boundary equilibrium collision. In this paper we show that the problem has been incompletely addressed, even in planar systems, revealing the care needed in handling fundamental issues in piecewise smooth dynamics.

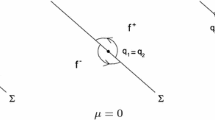
Consider the two-dimensional piecewise smooth system

$$\begin{aligned} (\dot{x},\dot{y})= {\left\{ \begin{array}{ll} \left( {P^+(x,y),Q^+(x,y)}\right) &{}\quad \text {if y>0},\\ \left( {P^-(x,y),Q^-(x,y)}\right) &{}\quad \text {if y<0}, \end{array}\right. } \end{aligned}$$

(2)

where $\Sigma =\left\{ (x,y)\in {\mathbb {R}}^2:y=0\right\}$. We are concerned with what happens when a simple equilibrium of $(P^+,Q^+)$ collides with $\Sigma$ when $\alpha =0$, if $(P^-,Q^-)$ is assumed to be transverse to $\Sigma$ and undergo no qualitative change as $\alpha$ varies.

That anything interesting happens at all is a result of how the flow interacts with the switching surface. Using Filippov’s convention (1988), if the normal components $Q^\pm (x,0)$ have the same sign then the flow crosses $\Sigma$, in the direction of increasing y if $Q^\pm (x,0)>0$, and of decreasing y if $Q^\pm (x,0)<0$. The flow becomes confined to $\Sigma$ if the normal components are in opposition, that is when $Q^+(x,0)Q^-(x,0)<0$, and then slides along the switching surface. The vector field that governs sliding is defined (again using Filippov’s convention 1988) as a convex combination of the vector fields in (2), given by

$$\begin{aligned} (\dot{x},\dot{y}) = \lambda \left( {P^+(x,0),Q^+(x,0)}\right) +(1-\lambda )\left( {P^-(x,0),Q^-(x,0)}\right) , \end{aligned}$$

(3)

for $\lambda \in [0,1]$. This should lie tangent to $\Sigma$ to give motion along it, implying $\dot{y}=0$, hence

$$\begin{aligned} \lambda =\frac{Q^-(x,0)}{Q^-(x,0)-Q^+(x,0)}\;. \end{aligned}$$

(4)

Substituting (4) into (3) gives

$$\begin{aligned} (\dot{x},\dot{y})=(P^0(x),0)\qquad \text{ where }\qquad P^0(x)= \frac{f(x)}{Q^-(x,0)-Q^+(x,0)}, \end{aligned}$$

(5)

where $(P^0(x),0)$ is the sliding vector field, whose numerator is

$$\begin{aligned} f(x)=P^+(x,0)Q^-(x,0)-P^-(x,0)Q^+(x,0)\;. \end{aligned}$$

(6)

For the system (2) we define an equilibrium in $y>0$ as a point where $P^+(x,y)=Q^+(x,y)=0$, and an equilibrium in $y<0$ as a point where $P^-(x,y)=Q^-(x,y)=0$. A boundary equilibrium is a point where $y=0$ and either $P^+(x,y)=Q^+(x,y)=0$ or $P^-(x,y)=Q^-(x,y)=0$. A pseudoequilibrium is a point on $y=0$ where $P^0(x)=0$, so we can also talk in a natural way of a pseudosaddle, a pseudonode and a pseudofocus.

A classification of boundary equilibrium collisions in the system described by (2), (5) and (6) was given by Filippov (1988). They occur as one-parameter bifurcations; some of their unfoldings were described in Kuznetsov et al. (2003), Carvalho and Tonon (2014) [and extended to two parameters in Guardia et al. (2011)], but not all cases already found in Filippov (1988) were included. Our aim in this paper to highlight not only the overlooked results of Filippov (1988), but also the methods used to achieve them.

Although very widely cited in piecewise smooth systems theory, we have long suspected that Filippov’s book (1988) was not being fully read or appreciated, so recently we set out to read the book from cover to cover. We quickly found that some of the deepest results of the book have been overlooked, whilst others have been rediscovered, and not always as powerfully as Filippov had already achieved. There are good reasons for such omissions. The book is a challenging read, with an out-dated structure, occasional repetition of ideas, and an ambiguous system of referencing. The material most relevant to modern dynamical systems appears late in the book, and hinges on a labyrinth of preceding theorems permeated with misprints or misleading translations.

In spite of this, it remains the most insightful and comprehensive work in the field, often more complete than some later works. We present an important example in this paper: two cases of one-parameter boundary equilibrium collisions in system (2) that are absent from recent classifications (Kuznetsov et al. 2003; Guardia et al. 2011; Carvalho and Tonon 2014; Bernardo et al. 2008).

We present Filippov’s methods in a modern context in Sect. 2 as far as they pertain to boundary equilibria. The simplicity and power of the ideas lie in identifying certain functions vital for a complete classification, and studying their singularities.

Although Filippov classified boundary equilibria, he did not unfold all of their bifurcations, and did not provide explicit ‘normal form’ equations for doing so. In Sect. 3 we present a suitable prototype system that produces all one-parameter boundary equilibrium collisions identified in Filippov (1988) (subsuming and correcting multiple expressions given elsewhere, in a single form). Table 1 presents the full classification and how they relate to classes given in Filippov (1988) and Kuznetsov et al. (2003). When we unfold these collisions, we obtain the bifurcations described in Kuznetsov et al. (2003), as well as two further cases, one that was fully unfolded in Filippov (1988), and another case that is presented here for the first time, in Sect. 3.3. Some closing remarks are made in Sect. 4.

2 Filippov’s Methodology

There are many different aspects to Filippov’s work (1988), and we describe the main elements for classifying boundary equilibria below. To help the reader access his work we give references in the format [§s.t p.u] referring to section s, subsection t, page u of the book. We keep to Filippov’s notation whenever possible.

The topological approach used in Filippov (1988) for the study of singularities and bifurcations can be summarized by considering two features. The first is the local singularity created by the vanishing of two or more scalar functions. Specifically, for a planar system (2), these are the functions

$$\begin{aligned} h,\quad P^+,\quad Q^+,\quad P^-,\quad Q^-,\quad f, \end{aligned}$$

(7)

where h is the function whose level set $h(x,y)=0$ defines the switching surface (taken in (2) to be $h(x,y)=y$), while $P^\pm$, $Q^\pm$, are the vector field components, and f is the numerator of the sliding vector field. The zeros of these create generic singularities in the plane as follows:

• the intersection of the sets $P^+=0$ and $Q^+=0$, or of $P^-=0$ and $Q^-=0$, is an equilibrium, its type determined by the signs of $\sigma$, $\Delta$, $\sigma ^2-4\Delta$, where $\sigma$ and $\Delta$ are the trace and determinant of ${\partial (P^+,Q^+)}/{\partial (x,y)}$ (or ${\partial (P^-,Q^-)}/{\partial (x,y)}$ respectively) at the equilibrium;

• the intersection of the set $h=0$ and $Q^+=0$ is a tangency (fold), curving away (visible) or toward (invisible) the switching surface as determined by whether ${\partial Q^+}/{\partial x}$ is positive or negative respectively (and conversely for an intersection of $h=0$ and $Q^-=0$);

• the intersection of the set $h=0$ and $f=0$ is a pseudoequilibrium, of node or saddle type determined by whether $\mathrm {d}{f}/\mathrm {d}{x}$ is negative or positive, respectively (assuming the sliding region is attractive).

Degeneracies of these occur where further functions from (7) vanish, or where the zero sets of these functions are non-transversal.

The second factor of the topological approach is separatrices, which are trajectories that form connections between singular points, whose definition is extended in [§17.1 p.190] to include all pointwise singularities of piecewise smooth systems. As for smooth systems, separatrices form boundaries in phase space between regions of trajectories with qualitatively different behavior. (The role of separatrices is also emphasized in the work of Teixeira (e.g., Guardia et al. 2011) and in global sliding bifurcations (Bernardo et al. 2008.)

In the rest of this section below, we describe in more detail how these principles are used to classify boundary equilibria.

2.1 Classifying Boundary Equilibria

Filippov begins the investigation of ‘singular points on a line of discontinuity’ in [§19 p.217]. He shows that there are six different types of singular points where $Q^+(x,0),$ $Q^-(x,0)$ and $P^0(x)$ can vanish, and his “type 4” singularities [§19.2 p.243] are our sole concern here. These describe collision with $\Sigma$ of an equilibrium in $y>0$, when the flow is simple in $y<0$ (meaning the $(P^-,Q^-)$ system has no equilibria or tangencies with $\Sigma$).

There are eight topological classes of such singularities, found as follows. Let $(x,y)=(0,0)$ be a simple boundary equilibrium such that

$$\begin{aligned} P^+(0,0)= Q^+(0,0)=0,\quad Q^-(0,0)\ne 0, \qquad \text {at } \alpha =0. \end{aligned}$$

(8)

This means an equilibrium of $(P^+,Q^+)$ lies on $\Sigma$, while $(P^-,Q^-)$ is directed transverse to $\Sigma$. Let $\Delta =\det \varvec{J}$ and $\sigma = {{\mathrm{tr}}}\varvec{J}$ be the determinant and trace of the Jacobian

$$\begin{aligned} \varvec{J}=\frac{\partial (P^+,Q^+)}{\partial (x,y)}\biggr |_{(0,0)}. \end{aligned}$$

(9)

The equilibrium can be one of the three kinds: a saddle if $\Delta < 0$, a node if $\Delta >0$ and $\sigma ^2-4\Delta > 0$, and a focus if $\Delta >0$ and $\sigma ^2-4\Delta < 0$. If $\Delta >0$, the quantity $\sigma Q^-(0,0)$ tells us whether the vector fields either side of $\Sigma$ both point toward or both away from (0, 0) (when $\sigma Q^-(0,0)<0$), or one points toward and one points away (when $\sigma Q^-(0,0)>0$).

In the generic case when $Q^+_x(0,0) \ne 0$, the quantity $Q^-(x,0)Q^+(x,0)$ changes sign as x passes through $x=0$. Hence there can only be sliding on one side of the singularity, either $x<0$, $y=0$, or $x>0$, $y=0$.

It follows immediately from $Q^+(0,0)=0$, (5) and (6) that $f(0)=0$, hence $(x,y)=(0,0)$ is also a pseudoequilibrium, since $Q^-(0,0)\ne 0$. The derivative ${f}^{\prime }(0)$ describes the variation of the sliding vector field across the singularity. If ${f}^{\prime }(0)<0$, then the sliding vector field and the vector field in $y<0$ point either both toward or both away from (0, 0). If ${f}^{\prime }(0)>0$, then one of these fields points toward (0, 0) and the other away. The case ${f}^{\prime }(0)=0$ is degenerate, and not considered here.

It is now simply a counting exercise to consider permutations of the signs of the quantities $\Delta$, $\sigma ^2-4\Delta$, ${f}^{\prime }(0)$, and $\sigma Q^-(0,0)$, noting that some permutations are equivalent up to symmetries $t\mapsto -t$ and $x\mapsto -x$, to show that there are eight topological classes of singularities (two each for the saddle and focus, four for the node). These are illustrated in Fig. 1 and listed in Table 1.

Fig. 1

The eight planar boundary equilibria. Labels correspond to Filippov’s figure numbers from Filippov (1988), also listed in Table 1, column 7. Note that panels F92 and F94 are drawn with time in the opposite direction to that in Filippov (1988)

Table 1 Boundary equilibrium bifurcations

When we consider the bifurcations formed by these singularities as $\alpha$ passes through zero, we obtain further subclasses either due to the sign of $\sigma Q^-(0,0)$, or because a different arrangement of separatrices produces topologically different phase portraits when the singularity is perturbed. These give rise to the twelve different subclasses in Table 1.

To prove the completeness of the classification in Table 1 requires topological methods from Filippov’s book which we summarize in the next section, culminating in Theorem 2, which fully classifies boundary equilibrium bifurcations. Once these topological methods have been used to assure that all possible bifurcations have been accounted for, it is then simple to construct a prototype system that attains all different classes for different parameter values. We provide such an expression in Sect. 3.

2.2 Equivalence and Structural Stability

Most ideas about smooth dynamical systems need updating when dealing with a piecewise smooth system. For example, the notion of a trajectory needs extension, to account for finite time effects (see [§12.2 p.124]). Piecewise smooth systems exhibit non-uniqueness since many different trajectories can arrive at $\Sigma$ and slide. To deal with this problem, Filippov [§16.3 p.184] modified the definition of topological equivalence. Two piecewise smooth systems are said to be (piecewise) topologically equivalent provided: (a) each trajectory arc (or stationary point) of the first system maps into a trajectory arc (or stationary point) of the second system, and (b) the inverse mapping maps each trajectory arc (or stationary point) of the second system into a trajectory arc (or stationary point) of the first system. The mapping may change the direction of motion along some trajectory segments and not others, as discussed with examples in [§16.3 p.184].

A point $(x,y) \in G_i$ is ordinary if a neighborhood of (x, y) contains no stationary points and is (piecewise) topologically equivalent to a neighborhood consisting of segments of parallel straight lines. The remaining points are singular points. These are sets of stationary points (x, y) where $P^i(x,y)=Q^i(x,y)=0$ (an equilibrium), $P^0(x)=0$ (a pseudoequilibrium), or tangencies on $\Sigma$ (or its edges). If a set of singular points forms a line (segment), it is termed a linear singularity.

Piecewise smooth separatrices are defined in [§17.1 p.190]. The classical definition of a separatrix is any orbitally unstable half-trajectory (semipath) tending to an equilibrium. In piecewise smooth systems it is not only equilibrium states which can have separatrices, but also all pointwise singularities, including points of non-uniqueness, and these can be orbitally stable. For the purpose of our proof we only need to consider separatrices to pseudoequilibria in addition to the smooth separatrix definition.

We also need the notions of polytrajectory and double separatrix. A polytrajectory is a line consisting of arcs of trajectories, which does not pass through singular points and consists of no arcs of linear singularities. A trajectory, or polytrajectory, both end arcs of which are separatrices, is called a double separatrix.

A piecewise smooth system is structurally stable if it preserves its topological structure under any sufficiently small admissible perturbation. Filippov [§18.1 p.206] introduces systems of class $C^p_*$, which are piecewise smooth systems (1) in which: $(P^i,Q^i)$ is $C^p$ (p times differentiable) in $\overline{G}_i$, $\Sigma$ is $C^{p+1}$ ($p+1$ times differentiable), and $\Sigma$ is the same for all systems in the class. Then we have the following theorem [§18.4 p.217]:

Theorem 1

For a planar piecewise smooth system (1) of class ${\mathcal {C}}^1_*$ to be structurally stable in a closed bounded domain D, it is necessary and sufficient that it has no double separatrices, only a finite number (possibly zero) of structurally stable point singularities, and only a finite number (possibly zero) of structurally stable closed polytrajectories.

This theorem (a generalization of the Andronov–Pontryagin theorem) was proved first by Kozlova (1984)¹.

Filippov then shows that one-parameter perturbations of the eight singularities form structurally stable systems, i.e., the singularities have codimension one. It is quite easy to show [§19.6 p.244–5 (Lemma 12)] that the equilibrium of $(P^+,Q^+)$ persists under perturbation, and that, provided ${\partial Q^+}/{\partial x}|_{(0,0)}\ne 0$ and that considering $(P^+,Q^+)$ over the whole plane (not only in $y>0$), the equilibrium is structurally stable and its separatrices (stable/unstable manifolds) are locally transverse to the switching manifold, and remain so under perturbation.

Necessary and sufficient conditions for the singularity at (0, 0) to have codimension one are given in [§19.6 p.246 (Theorem 5)]. These conditions state that the quantities

$$\begin{aligned} \Delta ,\quad \sigma ,\quad \sigma ^2-4\Delta ,\quad {\partial Q^+}/{\partial x},\quad {f}^{\prime }, \end{aligned}$$

evaluated at (0, 0) are nonzero, plus conditions which prevent the formation of a double separatrix. The double separatrices which must be ruled out are a trajectory connecting a saddle and a pseudonode (in case ‘F89’ in Fig. 1; Table 1), or a trajectory connecting a visible fold to a pseudosaddle in the presence of a focus [in case ‘F96’ in Fig. 1; Table 1; this ‘degenerate boundary focus’ is discussed in [§19.6 p.245–246 (Lemma 13)] and Figure 6 of Kuznetsov et al. (2003)]. The proof [§19.6 p.246–249] makes extensive use of Theorem 1 above.

Now we can prove the completeness of the classification in Table 1.

Theorem 2

The eight Filippov “type 4” boundary equilibria have a total of 12 unfoldings, as listed in Table 1.

Proof

When the equilibrium at (0, 0) is a node, we have $\Delta >0$ and $\sigma ^2-4\Delta >0$. According to Sect. 2.1, there are four topologically different cases at $\alpha =0$ generated by the different signs of ${f}^{\prime }(0)$ and $\sigma Q^-(0,0)$ (describing respectively whether the sliding flow points toward or away from (0, 0), and whether the flow in $y<0$ points toward or away from (0, 0)). Only two of these unfoldings were given in Kuznetsov et al. (2003), corresponding to cases $BN_{1,2}$; we show the other two in Fig. 2 in Sect. 3.3.

For a saddle with $\Delta <0$ (implying $\sigma ^2-4\Delta >0$), by Sect. 2.1 we have two cases to consider depending on the sign of ${f}^{\prime }(0)$. When ${f}^{\prime }(0)<0$, the saddle disappears in the bifurcation, and a pseudosaddle appears in its place. When ${f}^{\prime }(0)>0$ the saddle coexists with a pseudonode for $\alpha >0$, and a double separatrix can form connecting the saddle and the pseudonode. Hence this case is further subdivided, depending on whether the separatrix of the pseudonode hits the crossing region or not. The two sub-cases are described in condition 4 of Theorem 5 in [§19.6 p.246–249]. This gives three unfoldings corresponding to cases $BS_{1,2,3}$ from Kuznetsov et al. (2003).

For the focus we have $\Delta >0$ and $\sigma ^2-4\Delta <0$, and by Sect. 2.1 there are four cases to consider depending on the signs of $\sigma Q^-(0,0)$ and ${f}^{\prime }(0)$. When ${f}^{\prime }(0)>0$ the focus and a pseudonode exist for opposite signs of $\alpha$, for $\sigma Q^-(0,0)<0$ these have the same attractivity, for $\sigma Q^-(0,0)>0$ these have opposite attractivity and the bifurcation involves the (dis)appearance of a limit cycle. These are cases $BF_{3,4}$ in Kuznetsov et al. (2003). When ${f}^{\prime }(0)<0$ the focus and a pseudosaddle coexist for the same sign of $\alpha$; for $\sigma Q^-(0,0)<0$ the trajectory through the visible fold misses the sliding region, and for $\sigma Q^-(0,0)>0$ the trajectory through the visible fold can connect to the pseudosaddle forming a double separatrix. This gives rise to two sub-cases when the separatrix of the pseudosaddle either hits the crossing region or spirals up to the focus. The two latter sub-cases are described in condition 5 of Theorem 5 in [§19.6 p.246–249], and the degenerate boundary focus condition in Kuznetsov et al. (2003). This generates the three cases $BF_{5,1,2}$ from Kuznetsov et al. (2003). $\square$

3 A Prototype for Boundary Equilibrium Collisions

Rather than describe the unfoldings of the various bifurcations at length, in this section we provide a prototype system of equations that is sufficient to obtain all eight of the boundary equilibria in Fig. 1, and to obtain all 12 of their unfoldings as in Table 1. We will unfold two cases missed from recent classifications; the others can be found in Kuznetsov et al. (2003).

A prototype that unites all codimension-one boundary equilibrium collisions, and their unfoldings, is given by (2) with

$$\begin{aligned} \begin{array}{llll} P^+(x,y)=a(y-\alpha )-x,&{}\quad &{} Q^+(x,y)=abx-y+\alpha ,\\ P^-(x,y)=\sin c,&{}\quad &{}Q^-(x,y)=\cos c, \end{array} \end{aligned}$$

(10)

where $\alpha \in {\mathbb {R}}$ is the bifurcation parameter, while $a>0$, $b=\pm 1$ and $c\in [0,2\pi )\setminus \{\pi /2,3\pi /2\}$, are constants.

The flow crosses $\Sigma$ transversally at points (x, y) where $y=0$ and $Q^+(x,0)Q^-(x,0)=(abx+\alpha )\cos c>0$. Sliding occurs for $y=0$ and x such that $Q^+(x,0)Q^-(x,0)=(abx+\alpha )\cos c<0$, the sliding vector field from (5) being

$$\begin{aligned} \dot{x}=P^0(x)= \frac{f(x)}{\alpha +abx-\cos c}, \end{aligned}$$

(11)

with $f(x) = (x+a\alpha )\cos c+(abx+\alpha )\sin c$. Hence

$$\begin{aligned} {f}^{\prime }(0)= \cos c+ab\sin c, \end{aligned}$$

(12)

so ${f}^{\prime }(0) \ne 0$ in general. Note that $Q^+_x(0,0) = ab \ne 0$. The dynamics of (10) is made up of three elements: the flow above ($y>0$), below ($y<0$) and on $\Sigma$ ($y=0$). First we consider the dynamics in $y>0$, then $y=0$, and then the consequences of concatenating them. Although the dynamics in $y<0$ is regular, the choice of the constant c plays an important role.

3.1 Dynamics for $y>0$

Equation (10) for $y>0$ has a unique equilibrium at $(x,y)=(0,\alpha )$. When $\alpha =0$ the equilibrium collides with $\Sigma$. Since the system in $y>0$ is linear, the phase portraits in the neighborhood of the equilibrium are entirely described by the Jacobian at the equilibrium, that is,

$$\begin{aligned} \varvec{J}|_{(0,\alpha )}=\frac{\partial (P^+,Q^+)}{\partial (x,y)}\biggr |_{(0,\alpha )}=\begin{pmatrix}-1&{}a\\ ab&{}-1\end{pmatrix}. \end{aligned}$$

The determinant $\Delta =\det \varvec{J}$ and trace $\sigma = {{\mathrm{tr}}}\varvec{J}$ distinguish among the possibilities:

$$\begin{aligned} \begin{array}{lclll} \Delta< 0 &{}\quad \Leftrightarrow \quad &{} a^2b>1&{}\quad :\quad &{}\text {saddle},\\ \Delta> 0,\; \sigma ^2-4\Delta> 0 &{}\quad \Leftrightarrow \quad &{} a^2b<1,\;b>0&{}\quad :\quad &{}\text {node},\\ \Delta > 0,\; \sigma ^2-4\Delta< 0 &{}\quad \Leftrightarrow \quad &{} a^2b<1,\;b<0&{}\quad :\quad &{}\text {focus}.\end{array} \end{aligned}$$

In the saddle case (‘$BS_{1,2}$’), the intersections of the stable and unstable manifolds with the switching surface play a crucial role in classifying bifurcations, hence we need the eigenvectors of the Jacobian $\varvec{J}$, which are $(\pm 1, \sqrt{b})$. The intersections of the switching surface and the stable/unstable manifolds occur at $x=\pm \alpha /\sqrt{b}$.

In the case of a focus (‘$BF_{1,2}$’), the separatrix that connects the tangency of the upper vector field with the switching surface to another point on the switching surface plays a similarly crucial role. The position of this connection is derived in Filippov (1988) and Kuznetsov et al. (2003).

3.2 Dynamics on $y=0$

The sliding vector field (11) has a pseudoequilibrium at $(x_{\text {p}},0)$ where

$$\begin{aligned} x_{\text {p}}=-\alpha \dfrac{a \cos c+\sin c}{a b \sin c+\cos c}, \end{aligned}$$

(13)

provided that the point $x_{\text {p}}$ is in the sliding region. This is guaranteed for one or other sign of $\alpha$ for any choice of a, b, c. The attractivity of $x_{\text {p}}$ is determined by the derivative of $P^0(x)$ evaluated at $x=x_{\text {p}}$, given by

$$\begin{aligned} \left. \frac{\mathrm {d}P^0}{\mathrm {d}x}\right| _{x=x_{\text {p}}} = \frac{1}{\alpha +abx_{\text {p}}-\cos c}{f}^{\prime }(x_p),\quad {f}^{\prime }(x_p)=\cos c+ab\sin c\;. \end{aligned}$$

In particular for $\alpha =0$ this becomes

$$\begin{aligned} \left. \frac{\mathrm {d}P^0}{\mathrm {d}x}\right| _{x=0} = \frac{1}{abx_{\text {p}}-\cos c}{f}^{\prime }(0),\quad {f}^{\prime }(0)=\cos c+ab\sin c\;. \end{aligned}$$

(14)

3.3 Unfoldings of the Node

The analysis above is sufficient to unfold all codimension-one boundary equilibrium bifurcations in (10). The unfoldings take place as $\alpha$ changes sign, and the 12 different cases occur in different well-defined open regions of (a, b, c) parameter space. The parameter values that give different arrangements of separatrices are found by seeking the values that give a double separatrix (a pseudosaddle that grazes $\Sigma$ in case ‘$BF_{1,2}$’, a pseudonode that connects to a saddle in case ‘$BS_{1,2}$’); this is a lengthy exercise covered in Filippov (1988) and Kuznetsov et al. (2003), and we will not consider these cases in detail.

Varying the different quantities gives the complete boundary collision classification shown in Table 1.

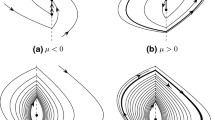
The two cases missing from Kuznetsov et al. (2003) are illustrated in Fig. 2. These are the boundary-node bifurcations arising from Filippov’s Figures 92–93, in which the equilibrium at $(0,\alpha )$ is a node for $\alpha >0$. Phase portraits for (b) only were shown in Filippov (1988). It is sufficient to take $a=-1/2$, $b=1$. The criterion for the existence of a pseudoequilibrium reduces to $\alpha \cos c>0$.

Fig. 2

The missing boundary equilibrium bifurcations: a a node exchanges stability with a pseudonode as it collides with $\Sigma$; b a node undergoes a saddle-node bifurcation with a pseudosaddle, to which it is connected via the tangency

The bifurcations that take place as $\alpha$ changes sign are also illustrated in Fig. 2. An example of the unfolding shown in Fig. 2a is given by $c=7\pi /5$, so $\cos c=(1-\sqrt{5})/4$, and an example of the unfolding shown in Fig. 2b is given by $c=2\pi /5$, so $\cos c=(-1+\sqrt{5})/4$; in both cases $\tan c=\sqrt{5+2\sqrt{5}}$.

As an example consider the case $c=7\pi /5$, for which Fig. 2a shows the unfolding. Consider first the vector fields in $y>0$, $y<0$, and $y=0$. From (10) and (11) we have

$$\begin{aligned} (\dot{x},\;\dot{y})= & {} {\left\{ \begin{array}{ll} \left( {\frac{1}{2}(\alpha -y)-x,\;\alpha -\frac{1}{2}x-y}\right) &{}\quad \text {if }y>0,\\ \left( {-\frac{1}{4}\sqrt{2(5+\sqrt{5})},\;\frac{1}{4}(1-\sqrt{5})}\right) &{}\quad \text {if }y<0,\\ \left( {\dfrac{(x-\frac{1}{2}\alpha )(1-\sqrt{5})+(\alpha -\frac{1}{2}x)\sqrt{2(5+\sqrt{5})}}{4\alpha -2x-1+\sqrt{5}},\;0}\right) &{}\quad \text {if }y=0, x<2\alpha , \end{array}\right. }\nonumber \\ \end{aligned}$$

(15)

the third row being the sliding vector field (5).

The lower vector field points away from $\Sigma$ at an angle $c-\pi /2=9\pi /10$ to the positive x-axis. The upper vector field has an attracting node at $(x,y)=(0,\alpha )$, which therefore only exists in (15) if $\alpha >0$, where the Jacobian $\left( {\begin{array}{cc}-1&{}-1/2\\ -1/2&{}-1\end{array}}\right)$ has eigenvalues $\lambda =-1\pm \frac{1}{2}$ with eigenvectors $(\mp 1,1)$. At the point $(x,y)=(2\alpha ,0)$ the vector field has tangential contact with $y=0$, the flow curving away from $y=0$ (visible tangency) if $\alpha >0$ and curving toward $y=0$ (invisible tangency) if $\alpha <0$.

The sliding vector field has a repelling pseudonode at $(x,y)=(x_{\text {p}},0)$ where $x_{\text {p}}=\alpha (1-2\sqrt{5+2\sqrt{5}})\big /(2-\sqrt{5+2\sqrt{5}})$. The sliding region exists only for $x<2\alpha$, with $(\dot{x},\dot{y})=(-3\alpha /2,0)$ at the boundary $x=2\alpha$, i.e., at the tangency.

By putting these elements together, one can sketch the phase portraits in the neighborhood of the bifurcation at $\alpha =0$, as shown in Fig. 2a. We have reversed time in the figure for ease of comparison with (b), in which the stability of the node at $(0,\alpha )$ for $\alpha >0$ is reversed. The analysis for $c=2\pi /5$ proceeds similarly and leads to the phase portraits shown in Fig. 2b.

4 Concluding Remarks

The bifurcations in Fig. 2 have not appeared in any recent study to our knowledge, despite existing under generic assumptions as a single parameter is varied, requiring no special conditions and constituting a non-trivial class of systems. We have deliberately avoided calling (10) a topological normal form, because the usage of normal forms in Kuznetsov et al. (2003), Guardia et al. (2011), Carvalho and Tonon (2014) has not assured the completeness of classifications, and topological methods remain at present more reliable. The singular cases ($\alpha =0$) depicted in Fig. 2 were given in Filippov (1988) via topological classification, yet were missing from studies of normal forms in Kuznetsov et al. (2003), Bernardo et al. (2008). Although mention was made in Guardia et al. (2011) of an omission from Kuznetsov et al. (2003), the missing cases were neither specified nor shown to provide anything distinct from the known cases.

It is striking how simple the boundary equilibrium classification is to obtain, given the right ingredients. In fact we can assume $Q^-(0,0)>0$ in (2), without loss of generality, then we only need to know:

• the type of equilibrium of $(P^+(0,0),Q^+(0,0))$ (saddle, focus, attracting node, repelling node),

• the sign of $f^{\prime }(0)$.

It is the second part, the sign of $f^{\prime }(0)$, that has been overlooked in all but Filippov’s work, but using this we can generate Filippov’s classification almost trivially. Let S denote a saddle, F denote a focus, n denote an attracting node and N a repelling node, and let I/O denote an inward/outward sliding vector field with respect to the singularity. Combining the equilibrium type and sliding direction we immediately have the eight boundary equilibrium classes SI, SO, nI, NI, nO, NO, FI, FO, corresponding to Filippov’s figures 89–96, as shown in Fig. 1. Each class will have at least one unfolding, with more than one unfolding if double separatrices must be avoided. The unfoldings in Fig. 2 are the cases NI and nO.

Filippov also classifies in [§19.2 p.218] the other singular scenarios that arise due to multiple pseudoequilibria $f=0$ coinciding, tangencies of one or both vector fields to the switching surface $Q^\pm (x,0)=0$, and coincidence of an equilibrium of one vector field with a tangency or equilibrium of the other vector field at the switching surface. Furthermore, contrary to most recent treatments which proceed from generic scenarios to bifurcations of codimension one, codimension two, etc., Filippov discusses singular situations of arbitrary (including infinite) codimension. For $n\geqslant 3$, Filippov makes a brief mention in [§23.4 p.285], but otherwise very little is known about these “type 4” singular points, or their bifurcations in higher dimensions. There is mileage yet in closer reading of Filippov (1988) as the local theory of piecewise smooth dynamical systems continues to develop.

Data Access Statement  No new data were created during this study.