Global stability for epidemic models on multiplex networks

Abstract

In this work, we consider an epidemic model in a two-layer network in which the dynamics of susceptible–infected–susceptible process in the physical layer coexists with that of a cyclic process of unaware–aware–unaware in the virtual layer. For such multiplex network, we shall define the basic reproduction number $R_0^V$ in the virtual layer, which is similar to the basic reproduction number $R_0^P$ defined in the physical layer. We show analytically that if $R_0^P \le 1$ and $R_0^V \le 1$, then the disease and information free equilibrium is globally stable and if $R_0^P \le 1$ and $R_0^V > 1$, then the disease free and information saturated equilibrium is globally stable for all initial conditions except at the origin. In the case of $R_0^P > 1$, whether the disease dies out or not depends on the competition between how well the information is transmitted in the virtual layer and how contagious the disease is in the physical layer. In particular, it is numerically demonstrated that if the difference in $R_0^V$ and $R_0^P$ is greater than the product of $R_0^P$, the deviation of $R_0^V$ from 1 and the relative infection rate for an aware susceptible individual, then the disease dies out. Otherwise, the disease breaks out.

Appendix: A The derivation of model (1)

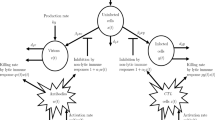
In this section, we derive the formulation of model (1). The discrete-time disease transmission model in Granell et al. (2013), based on the MMCA reads as follows.

$$\begin{aligned} \begin{aligned} p_i^{AI}(t+1)&= p_i^{AI}(t) (1-\mu ) + r_i^{US}(t) \left\{ [1-\gamma _i(t)] \left[ 1 - q_i^A(t)\right] + \gamma _i(t) \left[ 1 - q_i^U(t)\right] \right\} \\&\quad + q_i^{AS}(t) \left\{ \delta \left[ 1 - q_i^U(t)\right] + (1-\delta ) \left[ 1 - q_i^A(t)\right] \right\} \\&=: p_i^{AI}(t) (1-\mu ) + r_i^{US}(t) \, \text {Prob}(US\rightarrow AI) + q_i^{AS}(t) \, \text {Prob}(AS\rightarrow AI) \\ q_i^{AS}(t+1)&= p_i^{AI}(t)(1-\delta )\mu + r_i^{US}(t) [1-\gamma _i(t)] q_i^A(t) + q_i^{AS}(t) (1-\delta ) q_i^A(t),\\&=: p_i^{AI}(t)(1-\delta )\mu + r_i^{US}(t) \, \text {Prob}(US\rightarrow AS) + q_i^{AS}(t) \, \text {Prob}(AS\rightarrow AS),\\ r_i^{US}(t+1)&= p_i^{AI}(t)\delta \mu + r_i^{US}(t) \gamma _i(t)q_i^U(t) + q_i^{AS}(t) \delta q_i^U(t) \\&=: p_i^{AI}(t)\delta \mu + r_i^{US}(t) \, \text {Prob}(US\rightarrow US) + q_i^{AS}(t) \, \text {Prob}(AS\rightarrow US), \end{aligned} \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned} \gamma _i(t)&= \prod _{j\ne i} [ 1 - a_{ij} p_j^{AI} (t) \lambda ],\\ q_i^A(t)&= \prod _{j\ne i} [ 1 - b_{ij} p_j^{AI} (t) \beta ^A ],\\ q_i^U(t)&= \prod _{j\ne i} [ 1 - b_{ij} p_j^{AI} (t) \beta ^U ]. \end{aligned} \end{aligned}$$

(18)

Assuming the absence of dynamical correlation, $\gamma _i(t)$ is the transition probability at time t for individual i who is not being informed by any neighbors. Moreover, $q_i^A(t)$ (resp., $q_i^U(t)$) is probability at time t of an aware (resp., unaware) individual i not being infected by any neighbors. The second term $r_i^{US}\{[1-\gamma _i(t)][1-q_i^A(t)] + \gamma _i(t)[1-q_i^U(t)]\}$ on the first equation of (17) represents the probability of an unaware and susceptible individual becoming infected. We denote this term by $\text {Prob}(US\rightarrow AI)$. Similar notations are introduced in other terms in (17).

To derive the continuous version of disease transmission model (17), we first shorten the time interval for the iterations from $[t, t+1)$ to $[t, t+h)$ and then let h tend to 0. In the time interval $[t, t+h)$, we assume that all the parameters $\lambda , \delta , \beta ^U, \beta ^A$ and $\mu$ are replaced by $\lambda h, \delta h, \beta ^U h, \beta ^A h$ and $\mu h$, which means that the probabilities of those quantities depend linearly on the length of exposure. We shall write the resulting model as follows.

$$\begin{aligned} \begin{aligned} p_i^{AI}(t+h)&= p_i^{AI}(t) (1- \mu h) + r_i^{US}(t) \, \text {Prob}_h (US\rightarrow AI)\\&\quad + q_i^{AS}(t) \, \text {Prob}_h (AS\rightarrow AI), \\ q_i^{AS}(t+h)&= p_i^{AI}(t) (1- \delta h) \mu h + r_i^{US}(t) \, \text {Prob}_h (US\rightarrow AS)\\&\quad + q_i^{AS}(t) \, \text {Prob}_h (AS\rightarrow AS),\\ r_i^{US}(t+h)&= p_i^{AI}(t) \delta \mu h^2 + r_i^{US}(t) \, \text {Prob}_h (US\rightarrow US) \\&\quad + q_i^{AS}(t) \, \text {Prob}_h(AS\rightarrow US). \end{aligned} \end{aligned}$$

(19)

Moreover, for h sufficiently small, we have that

$$\begin{aligned} \begin{aligned} \text {Prob}_h(US\rightarrow AI)&= [ 1 - \gamma _i(t)] [1 - q_i^A(t)] + \gamma _i(t) [ 1 - q_i^U(t)] \\&= \left[ h \lambda \sum \limits _{j\ne i} a_{ij} p_j^{AI}(t) + O(h^2) \right] \left[ h \beta ^A \sum \limits _{j\ne i} b_{ij} p_j^{AI}(t) + O(h^2) \right] \\&\quad + \left[ 1 - h \lambda \sum \limits _{j\ne i} a_{ij} p_j^{AI}(t) + O(h^2) \right] \\&\qquad \left[ h \beta ^U \sum \limits _{j\ne i} b_{ij} p_j^{AI}(t) + O(h^2) \right] \\&= h \beta ^U \sum \limits _{j\ne i} b_{ij} p_j^{AI}(t) + O(h^2). \end{aligned} \end{aligned}$$

(20)

Similarly,

$$\begin{aligned} \text {Prob}_h(AS\rightarrow AI)&= h \delta \left[ 1 - q_i^U(t)\right] + (1- h \delta ) \left[ 1 - q_i^A(t)\right] \nonumber \\&= \left[ h^2 \delta \beta ^U \sum \limits _{j\ne i} b_{ij} p_j^{AI}(t) + O(h^3)\right] \nonumber \\&\quad + (1 - h\delta ) \left[ h \beta ^A \sum \limits _{j\ne i} b_{ij} p_j^{AI} (t) + O(h^2) \right] \nonumber \\&= h \beta ^A \sum \limits _{j\ne i} b_{ij} p_j^{AI} (t) + O(h^2). \end{aligned}$$

(21)

$$\begin{aligned} \text {Prob}_h(US\rightarrow AS)&= h \lambda \sum \limits _{j\ne i} a_{ij} p_j^{AI}(t) + O(h^2). \end{aligned}$$

(22)

$$\begin{aligned} \text {Prob}_h(AS\rightarrow AS)&= (1-h\delta )q_i^A(t) = 1-h \left[ \delta + \beta ^A \sum \limits _{j\ne i} b_{ij} p_j^{AI}(t) \right] + O(h^2). \end{aligned}$$

(23)

Using (19)–(23) and letting h tend to 0, we get

$$\begin{aligned} \begin{aligned} \dot{p}_i^{AI}&= - p_i^{AI}\mu +\beta ^Ur_i^{US}\sum \limits _{j\ne i} b_{ij}p_j^{AI} +\beta ^Aq_i^{AS}\sum \limits _{j\ne i} b_{ij}p_j^{AI},\\ \dot{q}_i^{AS}&= p_i^{AI}\mu +\lambda r_i^{US}\sum \limits _{j\ne i} a_{ij}p_j^{AI}-\beta ^A q_i^{AS}\sum \limits _{j\ne i} b_{ij}p_j^{AI}-\delta q_i^{AS},\\ \dot{r}_i^{US}&= - r_i^{US}\left[ \lambda \sum \limits _{j\ne i} a_{ij}p_j^{AI} + \beta ^U \sum \limits _{j\ne i} b_{ij}p_j^{AI} \right] + \delta q_i^{AS}. \end{aligned} \end{aligned}$$

(24)

Using the assumption that $p_i^{AI}+q_i^{AS}+r_i^{US}=1$, we arrive at Eqs. (1a) and (1b).