Oscillating epidemics in a dynamic network model: stochastic and mean-field analysis

Abstract

An adaptive network model using SIS epidemic propagation with link-type-dependent link activation and deletion is considered. Bifurcation analysis of the pairwise ODE approximation and the network-based stochastic simulation is carried out, showing that three typical behaviours may occur; namely, oscillations can be observed besides disease-free or endemic steady states. The oscillatory behaviour in the stochastic simulations is studied using Fourier analysis, as well as through analysing the exact master equations of the stochastic model. By going beyond simply comparing simulation results to mean-field models, our approach yields deeper insights into the observed phenomena and help better understand and map out the limitations of mean-field models.

Appendices

Appendix A: Bifurcation analysis of the mean-field model

In this appendix the steady states of system (1)–(4) and their stability is studied.

1.1 A1: Endemic steady state

The steady states are given by system (1)–(4) by putting zeros in the left hand sides (and omitting those parameters that are assumed to be zero), i.e. by system

$$\begin{aligned} 0&=\tau [SI] - \gamma [I], \end{aligned}$$

(8)

$$\begin{aligned} 0&=\gamma ( [II] - [SI])+ \tau ([SSI]-[ISI]-[SI])-\omega _{SI}[SI], \end{aligned}$$

(9)

$$\begin{aligned} 0&=-2\gamma [II] +2\tau ([ISI]+[SI]), \end{aligned}$$

(10)

$$\begin{aligned} 0&=2\gamma [SI] - 2\tau [SSI]+\alpha _{SS} ([S]([S]-1)-[SI]) \end{aligned}$$

(11)

where the closures

$$\begin{aligned}{}[SSI]=\frac{(k_{S}-1)[SS][SI]}{k_S[S]} \quad \text {and} \quad [ISI]=\frac{(k_{S}-1)[SI][SI]}{k_S[S]} \end{aligned}$$

(12)

are used with

$$\begin{aligned} k_{S}=\frac{[SS]+[SI]}{[S]} . \end{aligned}$$

For simplicity, the steady state values of the four variables are denoted here by [I], [SI], [II] and [SS]. All of them will be expressed in terms of [S] and then a quartic equation for [S] will be derived. It is obvious that $[I]=N-[S]$, then from (8) we get $[SI]=\frac{\gamma }{\tau }[I]$. Multiplying (9) by 2 and adding it to (10) and to (11) one can express [SS] in terms of [I] and [S] as

$$\begin{aligned}{}[SS]=[S]([S]-1)-2\frac{\omega _{SI}\gamma }{\alpha _{SS}\tau } [I]. \end{aligned}$$

(13)

From (10) we can express [II] in terms of [I] and [S] as

$$\begin{aligned}{}[II]=\frac{\tau [SI]}{\gamma } \left( \frac{[SI]}{[S]} - \frac{[SI]}{[SS]+[SI]} +1 \right) . \end{aligned}$$

(14)

Multiplying (9) by 2 and adding it to (10) we get

$$\begin{aligned} 2\tau [SSI] -2\gamma [SI] -2\omega _{SI} [SI] = 0 . \end{aligned}$$

Using the closure and dividing by 2[SI] yields

$$\begin{aligned} \frac{[SS]}{[S]} - \frac{[SS]}{[SS]+[SI]} = \frac{\gamma + \omega _{SI} }{\tau } . \end{aligned}$$

Now substituting $[SI]=\frac{\gamma }{\tau }(N-[S])$ and (13) into this equation one obtains the following quartic equation for $x=[S]$

$$\begin{aligned} x^4+A_3 x^3 + A_2 x^2 + A_1 x + A_0 =0 \end{aligned}$$

(15)

with

$$\begin{aligned} A_3&= 4ab-3-2b-c\\ A_2&= 2+2b+c+b^2+bc-6ab-4ab^2 -2abc + 4a^2b^2+Nb(1-4a)\\ A_1&= Nb(-1+6a-b-c+6ab+2ac-8a^2b)\\ A_0&= 2N^2ab^2(1-2a), \end{aligned}$$

where $a=\frac{\omega _{SI}}{\alpha _{SS}}$, $b=\frac{\gamma }{\tau }$ and $c=\frac{\omega _{SI}}{\tau }.$

Once (15) is solved for x, then the steady state ([I], [SI], [II], [SS]) is given by $[I]=N-x$, $[SI]=\frac{\gamma }{\tau }[I]$, (13) and (14). A solution x yields a biologically meaningful steady state if all of its coordinates are non-negative. An extensive numerical study showed that for any combination of the parameters there can be at most one endemic steady state. The endemic steady state exists if the disease-free equilibrium is unstable. The condition for that is determined in the next subsection. We note that the above calculation yields only the endemic steady states because during the derivation of the quartic equation there was a division by 2[SI], which is zero at the disease-free steady state.

1.2 A2: Stability of the disease-free steady state

The stability of the disease-free steady state is determined by the Jacobian matrix determined at $([I], [SI], [II], [SS])=(0,0,0,N(N-1))$. In order to compute this matrix we determine the partial derivatives of the triples at this steady state, as they are given by the closures (12).

$$\begin{aligned} \frac{\partial [SSI]}{\partial [I]}= & {} 0 , \quad \frac{\partial [SSI]}{\partial [SI]} = N-2 , \quad \frac{\partial [SSI]}{\partial [II]} = 0 , \quad \frac{\partial [SSI]}{\partial [SS]} = 0 ,\\ \frac{\partial [ISI]}{\partial [I]}= & {} 0 , \quad \frac{\partial [ISI]}{\partial [SI]} = 0 , \quad \frac{\partial [ISI]}{\partial [II]} = 0 , \quad \frac{\partial [ISI]}{\partial [SS]} = 0 , \end{aligned}$$

Using these partial derivatives the Jacobian matrix at the disease-free steady state can be given as

$$\begin{aligned} J = \begin{pmatrix} -\gamma &{}\quad \tau &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\gamma + \tau (N-2) - \tau -\omega _{SI}) &{}\quad \gamma &{}\quad 0 \\ 0 &{}\quad 2\tau &{}\quad -2\gamma &{} \quad 0 \\ \alpha _{SS}(1-2N) &{}\quad 2\gamma -2\tau (N-2) &{} \quad 0 &{}\quad -\alpha _{SS} \end{pmatrix}. \end{aligned}$$

It can be easily seen that $-\alpha _{SS}$ and $-\gamma$ are eigenvalues of this matrix. The remaining two eigenvalues are the eigenvalues of the $2\times 2$ matrix in the middle:

$$\begin{aligned} \begin{pmatrix} -\gamma + \tau (N-2) - \tau -\omega _{SI}) &{}\quad \gamma \\ 2\tau &{}\quad -2\gamma \end{pmatrix}. \end{aligned}$$

The disease-free steady state is asymptotically stable if and only if all the eigenvalues have negative real part. This has to be checked only for the above $2\times 2$ matrix. For a $2\times 2$ matrix the eigenvalues have negative real part if and only if its determinant is positive and its trace is negative. The determinant is positive if $\gamma + \omega _{SI} -\tau (N-2)>0$. The trace is positive if $3\gamma + \omega _{SI} -\tau (N-3)>0$. The first condition implies the second one, hence we proved Proposition 1.

1.3 A3: Stability of the endemic steady state

The stability of the endemic steady state can be determined only numerically. For a given set of the parameters the coordinates of the endemic steady state can be computed according to Appendix A1. The partial derivatives in the Jacobian J can be calculated analytically, then substituting the numerically obtained coordinates of the endemic steady state we get the entries of the Jacobian numerically. This enables us to calculate the coefficients of the characteristic polynomial

$$\begin{aligned} \lambda ^4-b_3\lambda ^3 +b_2\lambda ^2-b_1\lambda +b_0, \end{aligned}$$

where $b_3 = {{\mathrm{Tr}}}J$, $b_0 = \det J$ and $b_1,b_2$ can be given as the sum of some subdeterminants of the Jacobian, the concrete form of which is not important at this moment. To find the parameter values where Hopf bifurcation occurs we use the method introduced in Szabó et al. (2012). In the case of $4\times 4$ matrices the necessary and sufficient condition for the existence of pure imaginary eigenvalues is

$$\begin{aligned} b_0b^2_3= b_1(b_2b_3-b_1)\quad \text { and }\quad {{\mathrm{sign}}}b_1 = {{\mathrm{sign}}}b_3, \end{aligned}$$

(16)

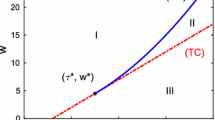
These relations will be considered here as necessary conditions for the Hopf-bifurcation. The transversality conditions will not be checked because of their complexity; instead, parameter values on the two sides of the bifurcation curve are chosen and the behaviour of the corresponding systems is checked numerically, to show that a Hopf-bifurcation really occurs along that curve. The Hopf-bifurcation set in the $(\tau ,\omega _{SI})$ parameter plane can be obtained as follows. For a given value of $\tau$ we compute the value of $b_0b^2_3= b_1(b_2b_3-b_1)$ numerically as $\omega _{SI}$ is varied. It turns out that for a range of $\tau$ values this expression changes sign twice as $\omega _{SI}$ is varied. More precisely, for given values of the other parameters ($N, \gamma , \alpha _{SS}$) there exist $\tau$ values $\tau _1$ and $\tau _2$, such that for $\tau \in (\tau _1, \tau _2)$ we get $\omega _1$ and $\omega _2$ such that for $\omega _{SI}=\omega _i$ ($i=1,2$) we have $b_0b^2_3= b_1(b_2b_3-b_1)$, i.e. Hopf bifurcation occurs at $\omega _{SI}=\omega _i$ ($i=1,2$). If $\tau$ is not in the interval $(\tau _1, \tau _2)$, then there is no Hopf bifurcation, i.e., the relation $b_0b^2_3= b_1(b_2b_3-b_1)$ cannot hold. For $\tau \in (\tau _1, \tau _2)$ and $\omega _{SI}\in (\omega _1,\omega _2)$ there is a stable periodic orbit. If $\omega _{SI}$ is outside the interval $(\omega _1,\omega _2)$, then there is no periodic orbit and either the endemic or the disease-free steady state is stable. The final state of the system is shown in the bifurcation diagram in Fig. 1.

Appendix B: State space and transition matrix for adaptive graphs with $N=2$ and $N=3$

In the case $N=2$, i.e., for a graph with two nodes, the number of edges is at most $E=1$. That is there are two graphs on two nodes, one is a single edge the other one consists of two disjoint nodes. We denote the states with $\{ SS, SI, IS, II\}$ when the graph consists of two disjoint nodes. Here the state SI means that node 1 is S and node 2 is I. The states are denoted by $\{ \overline{SS}, \overline{SI}, \overline{IS}, \overline{II} \}$ when the graph is a single edge. Thus the full state space for $N=2$ contains the following 8 states: $\{ SS, SI, IS, II, \overline{SS}, \overline{SI}, \overline{IS}, \overline{II}\}$. Consider now the transitions between these states. There are two types of transitions: epidemic transitions (infection and recovery) and network transitions (creating and deleting edges). Epidemic transitions may occur among states that belong to the same graph, that is within the subsets $\{ SS, SI, IS, II\}$ and $\{ \overline{SS}, \overline{SI}, \overline{IS}, \overline{II} \}$. Within the first subset only recovery may occur since these states belong to a graph that consists of two separate nodes. So the only possible transitions are $SI\rightarrow SS$, $IS\rightarrow SS$, $II\rightarrow IS$ and $II\rightarrow SI$, these may happen with rate $\gamma$. Within the subset $\{ \overline{SS}, \overline{SI}, \overline{IS}, \overline{II} \}$ infection may happen as well, hence the possible transitions are $\overline{SI}\rightarrow \overline{II}$ and $\overline{IS}\rightarrow \overline{II}$ with rate $\tau$ and $\overline{SI}\rightarrow \overline{SS}$, $\overline{IS}\rightarrow \overline{SS}$, $\overline{II}\rightarrow \overline{IS}$ and $\overline{II}\rightarrow \overline{SI}$ with rate $\gamma$. Network transitions occur between states in which the corresponding nodes are of the same type. For example, the transition $SS\rightarrow \overline{SS}$ occurs at rate $\alpha _{SS}$ since an SS type edge is created during this transition. Similarly, the transition $\overline{SS}\rightarrow SS$ occurs at rate $\omega _{SS}$ since an SS type edge is deleted during this transition. In general, the transition $AB\rightarrow \overline{AB}$ happens at rate $\alpha _{AB}$ and the transition $\overline{AB}\rightarrow AB$ happens at rate $\omega _{AB}$, where $A,B\in \{S,I\}$. All the transitions are shown in Fig. 9. If the states are ordered as $\{ SS, SI, IS, II, \overline{SS}, \overline{SI}, \overline{IS}, \overline{II}\}$, then the transition matrix of the corresponding Markov chain takes the form

$$\begin{aligned} M= \left( \begin{array}{cccc} M_{11}-A &{}\quad \Omega \\ A &{}\quad M_{22}- \Omega \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} M_{11}= & {} \left( \begin{array}{cccc} 0 &{}\quad \gamma &{}\quad \gamma &{}\quad 0\\ 0 &{}\quad -\gamma &{}\quad 0 &{}\quad \gamma \\ 0 &{}\quad 0 &{}\quad -\gamma &{}\quad \gamma \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -2\gamma \end{array} \right) , \quad M_{22}= \left( \begin{array}{cccc} 0 &{}\quad \gamma &{}\quad \gamma &{}\quad 0\\ 0 &{}\quad -\tau -\gamma &{}\quad 0 &{}\quad \gamma \\ 0 &{}\quad 0 &{}\quad -\tau -\gamma &{}\quad \gamma \\ 0 &{}\quad \tau &{}\quad \tau &{}\quad -2\gamma \end{array} \right) ,\\ A= & {} \left( \begin{array}{cccc} \alpha _{SS} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \alpha _{SI} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \alpha _{SI} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \alpha _{II} \end{array} \right) , \quad \Omega = \left( \begin{array}{cccc} \omega _{SS} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \omega _{SI} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \omega _{SI} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \omega _{II} \end{array} \right) . \end{aligned}$$

The matrices $M_{11}$ and $M_{22}$ contain the transition rates corresponding to the epidemic transitions. These rates belong to the transitions within the subsets $\{ SS, SI, IS, II\}$ and $\{ \overline{SS}, \overline{SI}, \overline{IS}, \overline{II} \}$, respectively. The matrices A and $\Omega$ contain the network transition rates that correspond to transitions between these two subsets. The master equation can be written as $\dot{x}(t) = M x(t)$, where the coordinates of the eight dimensional vector x(t) are the probabilities of the states at time t.

Let us briefly consider the case $N=3$. Then $E=3$, hence there are $2^3=8$ different possible graphs, one without any edges, three graphs with one edge, three line graphs with two edges and a triangle with three edges. Each graph can be in 8 possible states, namely $\{ SSS, SSI, SIS, ISS, SII, ISI, IIS, III\}$. Hence there are $2^3\cdot 2^3=64$ states altogether. Epidemic transitions may occur among states that belong to the same graph, for example, in the case of a triangle graph the transition $IIS\rightarrow III$ happens at rate $2\tau$, while its rate is $\tau$ for a line graph where node 2 is connected to node 1 and node 3. The transition rate may be zero, e.g., in the case when there is only one edge in the graph connecting nodes 1 and 2, or in the case when there are no edges at all in the graph. Network transitions occur between states in which the corresponding nodes are of the same type. For example, denoting by SSS the state where all nodes are susceptible and the graph consist of three disjoint nodes, and by $\overline{SS}S$ the state where all nodes are susceptible and the graph contains one edge that connects node 1 and 2, the rate of transition $SSS\rightarrow \overline{SS}S$ is $\alpha _{SS}$, while the rate of transition $\overline{SS}S\rightarrow SSS$ is $\omega _{SS}$. The master equations take again the form $\dot{x}(t) = M x(t)$, where the coordinates of the 64-dimensional vector x(t) are the probabilities of the states at time t.

We note that the size of the state space can be reduced by lumping some states together, similarly to the case of static graphs (Simon et al. 2010). The lumping of the state space for dynamic network processes is beyond the scope of this paper, here we only mention a few simple cases where lumping can be carried out. In the case $N=2$ it is easy to see that the states SI and IS can be lumped together, which means that their sum can be introduced as a new variable, and their differential equations can be added up. Similarly, the sum of $\overline{SI}$ and $\overline{IS}$ can be introduced as a new variable. (By adding their differential equations one can immediately see that the old variables will not appear in the remaining system of equations). Hence the eight-dimensional system $\dot{x}(t) = M x(t)$ can be reduced to a six-dimensional system by lumping. In the case $N=3$ we have even more chance for lumping if it is assumed that $\alpha _{SI}=0$, $\alpha _{II}=0$, $\omega _{SS}=0$, $\omega _{II}=0$. Without explaining the details we claim that in this case the 64-dimensional system of master equations can be reduced to a 20-dimensional one by lumping. In the case $N=4$ the dimension of the state space can be reduced from 1024 to 89.