Skip to main content
SpringerLink
Log in

A geometric analysis of fast-slow models for stochastic gene expression

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

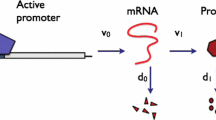
Stochastic models for gene expression frequently exhibit dynamics on several different scales. One potential time-scale separation is caused by significant differences in the lifetimes of mRNA and protein; the ratio of the two degradation rates gives a natural small parameter in the resulting chemical master equation, allowing for the application of perturbation techniques. Here, we develop a framework for the analysis of a family of ‘fast-slow’ models for gene expression that is based on geometric singular perturbation theory. We illustrate our approach by giving a complete characterisation of a standard two-stage model which assumes transcription, translation, and degradation to be first-order reactions. In particular, we present a systematic expansion procedure for the probability-generating function that can in principle be taken to any order in the perturbation parameter, allowing for an approximation of the corresponding propagator probabilities to that same order. For illustrative purposes, we perform this expansion explicitly to first order, both on the fast and the slow time-scales; then, we combine the resulting asymptotics into a composite fast-slow expansion that is uniformly valid in time. In the process, we extend, and prove rigorously, results previously obtained by Shahrezaei and Swain (Proc Natl Acad Sci USA 105(45):17256–17261, 2008) and Bokes et al. (J Math Biol 64(5):829–854, 2012; J Math Biol 65(3):493–520, 2012). We verify our asymptotics by numerical simulation, and we explore its practical applicability and the effects of a variation in the system parameters and the time-scale separation. Focussing on biologically relevant parameter regimes that induce translational bursting, as well as those in which mRNA is frequently transcribed, we find that the first-order correction can significantly improve the steady-state probability distribution. Similarly, in the time-dependent scenario, inclusion of the first-order fast asymptotics results in a uniform approximation for the propagator probabilities that is superior to the slow dynamics alone. Finally, we discuss the generalisation of our geometric framework to models for regulated gene expression that involve additional stages.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Amann H (1990) Ordinary differential equations. An introduction to nonlinear analysis, translated from the German by Gerhard Metzen. In: de Gruyter studies in mathematics, vol 13. Walter de Gruyter & Co., Berlin

  • Arrowsmith DK, Place CM (1990) An introduction to dynamical systems. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Abramowitz M, Stegun IA (eds) (1972) Handbook of mathematical functions with formulas, graphs, and mathematical tables, national bureau of standards. Applied mathematics series, vol 55. Dover Publications, New York

  • Balser W (1994) From divergent power series to analytic functions. In: Theory and application of multisummable power series. Lecture notes in mathematics, vol 1582. Springer, Berlin

  • Bennett MR, Hasty J (2009) Microfluidic devices for measuring gene network dynamics in single cells. Nat Rev Genet 10(9):628–638

    Article  Google Scholar 

  • Bernstein J, Khodursky A, Lin P, Lin-Chao S, Cohen S (2002) Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc Natl Acad Sci USA 99(15):9697–9702

    Article  Google Scholar 

  • Blasi T, Buettner F, Strasser M, Linnarsson S, Marr C, Theis FJ (2013) Cell-cycle effects obscure true kinetics of gene expression in single cell transcriptomics data. (in preparation)

  • Bokes P, King JR, Wood ATA, Loose M (2012) Exact and approximate distributions of protein and mRNA levels in the low-copy regime of gene expression. J Math Biol 64(5):829–854

    Article  MathSciNet  MATH  Google Scholar 

  • Bokes P, King JR, Wood ATA, Loose M (2012) Multiscale stochastic modelling of gene expression. J Math Biol 65(3):493–520

    Article  MathSciNet  MATH  Google Scholar 

  • Bowsher CG, Swain PS (2012) Identifying sources of variation and the flow of information in biochemical networks. Proc Natl Acad Sci USA 109(20):E1320–E1328

    Article  Google Scholar 

  • Cao Y, Gillespie DT, Petzold LR (2005) The slow-scale stochastic simulation algorithm. J Chem Phys 122(1):014116

    Article  Google Scholar 

  • Canalis-Durand M, Ramis JP, Schäfke R, Sibuya Y (2000) Gevrey solutions of singularly perturbed differential equations. J Reine Angew Math 518:95–129

    MathSciNet  MATH  Google Scholar 

  • Cotter SL, Zygalakis KC, Kevrekidis IG, Erban R (2011) A constrained approach to multiscale stochastic simulation of chemically reacting systems. J Chem Phys 135(9):094102

    Article  Google Scholar 

  • Cover TM, Thomas JA (2006) Elements of information theory. In: Wiley series in telecommunications and signal processing, 2nd edn. Wiley, Hoboken

  • Dumortier F, Roussarie R (1996) Canard cycles and center manifolds. Mem Am Math Soc 121(577)

  • Erban R, Kevrekidis IG, Adalsteinsson D, Elston TC (2006) Gene regulatory networks: a coarse-grained, equation-free approach to multiscale computation. J Chem Phys 124(8):084106

    Article  Google Scholar 

  • Fenichel N (1979) Geometric singular perturbation theory for ordinary differential equations. J Differ Equ 31(1):53–98

    Article  MathSciNet  MATH  Google Scholar 

  • Friedman N, Cai L, Xie XS (2006) Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Phys Rev Lett 97(16):168302

    Article  Google Scholar 

  • García-Martínezm J, González-Candelas F, Pérez-Ortín J (2007) Common gene expression strategies revealed by genome-wide analysis in yeast. Genome Biol 8:R222

    Article  Google Scholar 

  • Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81(25):2340–2361

    Article  Google Scholar 

  • Gillespie DT (1992) A rigorous derivation of the chemical master equation. Phys A 188(1–3):404–425

    Article  MathSciNet  Google Scholar 

  • Gillespie DT (2009) Deterministic limit of stochastic chemical kinetics. J Phys Chem 113(6):1640–1644

    Article  Google Scholar 

  • Golding I, Paulsson J, Zawilski SM, Cox EC (2005) Real-time kinetics of gene activity in individual bacteria. Cell 123(6):1025–1036

    Article  Google Scholar 

  • Grima R (2011) Construction and accuracy of partial differential equation approximations to the chemical master equation. Phys Rev E 84(5):056109

    Article  MathSciNet  Google Scholar 

  • Grima R, Schmidt D, Newman TJ (2012) Steady-state fluctuations of a genetic feedback loop: an exact solution. J Chem Phys 137(3):035104

    Article  Google Scholar 

  • Harper CV, Finkenstädt B, Woodcock DJ, Friedrichsen S, Semprini S, Ashall L, Spiller DG, Mullins JJ, Rand DA, Davis JRE, White MRH (2011) Dynamic analysis of stochastic transcription cycles. PLoS Biol 9(4):e1000607

    Article  Google Scholar 

  • Hek G (2010) Geometric singular perturbation theory in biological practice. J Math Biol 60(3):347–386

    Article  MathSciNet  MATH  Google Scholar 

  • Jahnke T, Huisinga W (2007) Solving the chemical master equation for monomolecular systems analytically. J Math Biol 54(1):1–26

    Article  MathSciNet  Google Scholar 

  • Jones CKRT (1995) Geometric singular perturbation theory. In Dynamical systems (Montecatini Terme, 1994). Lecture notes in Math., vol 1609. Springer, Berlin, pp 44–118

  • Kaern M, Elston TC, Blake WJ, Collins JJ (2005) Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet 6(6):451–464

    Article  Google Scholar 

  • Krupa M, Szmolyan P (2001) Extending geometric singular perturbation theory to non-hyperbolic points—fold and canard points in two dimensions. SIAM J Math Anal 33(2):286–314

    Article  MathSciNet  MATH  Google Scholar 

  • Lagerstrom PA (2010) Matched asymptotic expansions: ideas and techniques. In: Applied mathematical sciences, vol 76. Springer, New York

  • Laurenzi IJ (2000) An analytical solution of the stochastic master equation for reversible bimolecular reaction kinetics. J Chem Phys 113(8):3315–3322

    Article  Google Scholar 

  • Locke JC, Elowitz MB (2009) Using movies to analyse gene circuit dynamics in single cells. Nat Rev Microbiol 7(5):383–392

    Article  Google Scholar 

  • Mansour MM, Van den Broeck C, Nicolis G, Turner JW (1981) Asymptotic properties of markovian master equations. Ann Phys 131(2):283–313

    Article  MATH  Google Scholar 

  • Mastny EA, Haseltine EL, Rawlings JB (2007) Two classes of quasi-steady-state model reductions for stochastic kinetics. J Chem Phys 127(9):094106

    Article  Google Scholar 

  • McAdams H, Arkin A (1997) Stochastic mechanisms in gene expression. Proc Natl Acad Sci USA 94(3):814–819

    Article  Google Scholar 

  • Mukhopadhyay P (2011) An introduction to the theory of probability. World Scientific Publishing Co., Singapore

    Book  Google Scholar 

  • Murray JD (2008) Mathematical biology I: an introduction. In: Interdisciplinary applied mathematics, vol 17, 3rd edn. Springer, New York

  • Peccoud J, Ycart B (1995) Markovian modeling of gene-product synthesis. Theor Popul Biol 48(2):222–234

    Article  MATH  Google Scholar 

  • Popović N, Marr C, Swain PS (2015) A dynamical systems framework for parameter inference in stochastic gene expression. (in preparation)

  • Pendar H, Platini T, Kulkarni RV (2013) Exact protein distributions for stochastic models of gene expression using partitioning of Poisson processes. Phys Rev E 87(4):042720

    Article  Google Scholar 

  • Raser JM, O’Shea EK (2004) Control of stochasticity in eukaryotic gene expression. Science 304(5678):1811–1814

    Article  Google Scholar 

  • Risken H (1989) The Fokker–Planck equation: methods of solution and applications. In: Springer series in synergetics, vol 18, 2nd edn. Springer, Berlin

  • Schwanhäusser B, Busse D, Li N, Dittmar G, Schuchhardt J, Wolf J, Chen W, Selbach M (2011) Global quantification of mammalian gene expression control. Nature 473(7347):337–342 [Corrigendum: Nature 495(7439), 126–127, 2013]

  • Segel LA, Slemrod M (1989) The quasi-steady-state assumption: a case study in perturbation. SIAM Rev 31(3):446–477

    Article  MathSciNet  MATH  Google Scholar 

  • Strogatz SH (1994) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. In: Studies in nonlinearity. Addison-Wesley Publishing Company, Massachusetts

  • Swain P, Elowitz MB, Siggia ED (2002) Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc Natl Acad Sci USA 99(20):12795–12800

    Article  Google Scholar 

  • Shahrezaei V, Swain PS (2008) The stochastic nature of biochemical networks. Curr Opin Biotechnol 19:369–374

    Article  Google Scholar 

  • Shahrezaei V, Swain PS (2008) Analytical distributions for stochastic gene expression. Proc Natl Acad Sci USA 105(45):17256–17261

    Article  Google Scholar 

  • Sanft KR, Wu S, Roh M, Fu J, Lim RK, Petzold LR (2011) StochKit2: software for discrete stochastic simulation of biochemical systems with events. Bioinformatics 27(17):2457–2458

    Article  Google Scholar 

  • Suter DM, Molina N, Gatfield D, Schneider K, Schibler U, Naef F (2011) Mammalian genes are transcribed with widely different bursting kinetics. Science 332(6028):472–474

    Article  Google Scholar 

  • Thattai M, van Oudenaarden A (2001) Intrinsic noise in gene regulatory networks. Proc Natl Acad Sci USA 98(15):151588–151598

    Article  Google Scholar 

  • Thomas P, Straube AV, Grima R (2012) The slow-scale linear noise approximation: an accurate, reduced stochastic description of biochemical networks under timescale separation conditions. BMC Syst Biol 6(1):39

    Article  Google Scholar 

  • Verhulst F (2005) Methods and applications of singular perturbations: boundary layers and multiple timescale dynamics. In: Texts in applied mathematics, vol 50. Springer, New York

  • Viterbi A (1967) Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans Inf Theory 13(2):260–269

    Article  MATH  Google Scholar 

  • Wang Y, Liu C, Storey J, Tibshirani R, Herschlag D, Brown P (2002) Precision and functional specificity in mRNA decay. Proc Natl Acad Sci USA 99(9):5860–5865

    Article  Google Scholar 

  • Weinan E, Liu D, Vanden-Eijnden E (2005) Nested stochastic simulation algorithm for chemical kinetic systems with disparate rates. J Chem Phys 123(19):194107

    Article  Google Scholar 

  • Wiggins S (2003) Introduction to applied nonlinear dynamical systems and chaos. In: Texts in applied mathematics, 2nd edn. Springer, New York

  • Yu J, Xiao J, Ren X, Lao K, Xie X (2006) Probing gene expression in live cells, one protein molecule at a time. Science 311(5767):1600–1603

    Article  Google Scholar 

  • Zauderer E (2006) Partial differential equations of applied mathematics. In: Pure and applied mathematics (New York), 3rd edn. Wiley, Hoboken

  • Zopf CJ, Quinn K, Zeidman J, Maheshri N (2013) Cell-cycle dependence of transcription dominates noise in gene expression. PLoS Comput Biol 9(7):1–12

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, James Clerk Maxwell Building, King’s Buildings, Mayfield Road, Edinburgh, EH9 3JZ, UK

    Nikola Popović

  2. Institute of Computational Biology, Helmholtz Zentrum München, German Research Center for Environmental Health, Ingolstädter Landstraße 1, 85764, Neuherberg, Germany

    Carsten Marr

  3. SynthSys-Systems and Synthetic Biology, University of Edinburgh, CH Waddington Building, King’s Buildings, Mayfield Road, Edinburgh, EH9 3JD, UK

    Peter S. Swain

Authors
  1. Nikola Popović
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Carsten Marr
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peter S. Swain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikola Popović.

Additional information

Nikola Popović is grateful to Peter De Maesschalck and Ramon Grima for their careful reading of drafts of the manuscript and numerous helpful suggestions, as well as to Peter Szmolyan for stimulating discussions. Moreover, the authors acknowledge grant support from the Moray Endowment Fund, as well as from MAXIMATHS, an initiative by the School of Mathematics at the University of Edinburgh aimed at maximising the impact of mathematics in science and engineering. Finally, the authors thank three anonymous referees for valuable comments which greatly improved the original manuscript.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 468 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Popović, N., Marr, C. & Swain, P.S. A geometric analysis of fast-slow models for stochastic gene expression. J. Math. Biol. 72, 87–122 (2016). https://doi.org/10.1007/s00285-015-0876-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-015-0876-1

Keywords

Mathematics Subject Classification

Search

Navigation