1 Introduction

The development of the high-tech integrated circuits technology involves high power consumption and related heat generation; hence the cooling systems for microelectronic chips face the challenge of heat dissipation in confining spaces. Flow boiling in minichannels is an option because high heat transfer rate and minichannels are ideal for these applications due to their compactness and low pressure drop. Yet, these issues have not been studied enough. The research of the enhanced structures is increasingly attractive due to their theoretical enhancement potential for heat transfer. The summary of relevant literature focused on heat transfer in rectangular minichannels is presented in [1], and in addition, having enhanced surfaces—in [2, 3]. Trefftz method used for solving issues related to heat transfer in minichannels with new Trefftz functions is employed for smoothing measurement data and reducing measurement errors.

2 Experimental research

2.1 Experimental stand

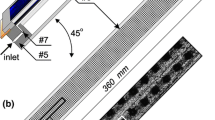
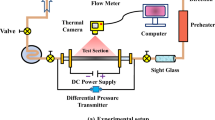
The area of interest is the issue of heat transfer in cooling liquid flowing through a rectangular minichannel with one uniformly heated enhanced wall. The flow system was discussed in [1–5]. The essential part of the experimental stand is the test section with a minichannel (Fig. 1, #1). It is 1 mm deep, 40 mm wide and 360 mm long, oriented vertically. The heating element for the working fluid (FC-72) flowing along the minichannel is alloy foil (#3) stretched between the front cover (#6) and the channel body (#5). This thin foil (approx. 0.1 mm) is enhanced on the side of the fluid flowing in the minichannel. It is energized by copper elements (#9) with direct current of controlled intensity. It is possible to observe both surfaces of the minichannel through two openings covered with glass panes. One pane (#4a) allows observing changes in the temperature of the foil surface. It is a plain side of the heating foil (between the foil and the glass), covered with thermosensitive liquid crystal paint (#3). The opposite surface of the minichannel (from the enhanced side of the heating foil) is observed through the other glass plane (#4b), which helps recognize the two-phase flow patterns. K-type thermocouples and two pressure converters (#7) are installed in the inlet and outlet of the minichannel. The data sources from the experiment and image acquisition system include: #10-Canon Eos 550D digital SLR camera, #11-Canon G11 digital camera, #14-two 1 kW halogen reflectors with forced air cooling and heat resistant casing, and #15-fluorescent and LED lamps emitting “cool white light”. Experimental data have been recorded with DaqBoard 2005 data acquisition station (#12) equipped with DASYLab software installed on a laptop (#13). The heating surface in the minichannel is provided with electric current by an inverter welder (#16) as current regulated DC power supply (up to 300 A). On the side of the foil contacting the fluid in the minichannel, mini-recesses were distributed unevenly in the selected area of the foil (40 × 40 mm) as shown in Fig. 2a. The recesses were obtained by spark erosion. The layer of melted metal of the foil and the electrode material, a few μm high, reaching locally 5 μm, accumulates around the cavities. The depth of the craters of cavities is usually below 1 μm. The photographs of the plain and enhanced foil is shown in Fig. 2b, c.

Fig. 1
figure 1

The schematic diagrams of the most elements of the experimental stand: #1-minichannel, #2-heating foil, #3-liquid crystal layer, #4a, b-glass pane, #5-channel body, #6-front cover, #7-thermocouple, #8-enhanced side of the foil, #9-copper element #10-digital SLR camera, #11-digital camera, #12-data acquisition station, #13-a laptop, #14-halogen reflectors, #15-fluorescent and LED lamps, #16-inverter welder, #17-shunt, #18-ammeter, #19-voltmeter

Full size image
Fig. 2
figure 2

The scheme of enhanced foil with mini-recesses a with photo b and 3-d topography c of the sample area

Full size image

2.2 Experimental methodology

Application of liquid crystals for the detection of two-dimensional heating surface temperature distribution must be preceded by colour (hue) temperature calibration [1].

FC-72 working fluid, at the temperature below its boiling point, flows laminarly into the minichannel (#1, Fig. 1). The gradual increase in the electric power supplied to the heating foil results in an increased heat flux transferred to the liquid in the minichannel. The current supplied via copper elements (#9) to the heating foil (#2) is controlled by an electrical system equipped with an inverter welder (#16). This leads to the incipience and next to the development of nucleate boiling. Then, the current supplied to the foil reduces gradually. Thanks to the liquid crystal layer located on its surface contacting the glass it is possible to measure the temperature distribution of the heating wall. Flow structure observation is carried out simultaneously at the opposite side of the minichannel.

Selected colour images of the heating foil in the measurement batch are presented in Fig. 3, the full batch was shown in [5]. When the current supplied to the heating foil increases gradually (images from #1 up to #4), it causes the occurrence of boiling incipience. The “boiling front” is recognizable as the hue sequence pattern, which indicates gradual hue changes to the liquid crystals and then sharp hue changes in the liquid crystal layer. Out-of-sensitivity-range temperatures are shown in black. This phenomenon of the occurrence of nucleation hysteresis was discussed in [1–6]. When the heat flux continues to increase, a new hue sequence in the upper part of images appears. This occurs when developed nucleate boiling is in progress in the minichannel. Then the current supplied to the foil is gradually reduced (images #5 and #6). Under such conditions, mild hue changes in the direction opposite to the spectrum sequence are observed. As a result, heat transfer returns to forced single phase convection. Images taken when the heat flux had been supplied to the foil were used for further analysis.

Fig. 3
figure 3

Colour heating foil images while increasing and later decreasing heat flux supplied to the foil, experimental parameters: flow velocity 0.17 m/s, mass flux 285 kg/(m2 s), Reynolds number Re = 880, inlet pressure 125 kPa, inlet liquid subcooling 42 K, dotted lines show location of mini-recesses

Full size image

2.3 Evaluation of the accuracy of heating foil temperature measurements with liquid crystal thermography

Error estimation is conducted in accordance with the principles of measurement accuracy analysis [7]. Root-mean-square error is adopted as a measure of error quantity. Root-mean-square errors are computed as the roots of the sum of the second powers of the products of function partial derivatives, with respect to an external parameter occurring in a direct measurement, by the mean error of a given parameter measurement.

The course of calculations used for the evaluation of the accuracy of heating foil temperature measurements with liquid crystals thermography is presented in [1]. Similarly to [1, 8], it is assumed that the mean temperature error for the single point, determined on the basis of hue in calibration experiment, amounts to:

$$\sigma = \frac{1}{P}\sum\limits_{i = 1}^{P} {\sigma_{i} } = \frac{1}{P}\sum\limits_{i = 1}^{P} {\sqrt {\left( {\frac{{\partial T(hue_{i} )}}{{\partial hue_{i} }}{\kern 1pt} \,\varDelta hue} \right)^{2} + \left( {2\,SEE} \right)^{2} + \left( {\varDelta T_{L} } \right)^{2} } } \,$$
(1)

where: i—measurement point; P—number of measurement points, T—temperature, Δhue—error in hue determination for a recorded and processed image; it is assumed it equals double standard deviation, determined on the basis of the data for sample surface image in calibration experiment; SEE—standard estimate of error in the fit of the calibration curve, determined with the use of the method of least squares, in accordance with formula:

$$SEE = \sqrt {\frac{{\frac{1}{P}\sum\nolimits_{i = 1}^{P} {\left( {T(hue_{i} ) - T_{i} } \right)^{2} } }}{P - m - n}}$$
(2)

where: m—the order of polynomial approximating a calibration curve, m = 16; n—derivative order, n = 1; ΔT L —absolute error in the measurement of liquid temperature during calibration.

Detailed calculations are presented in [9]. Absolute error in the measurement of liquid temperature at the minichannel inlet and outlet during calibration ΔT L consists of two errors: the one resulting from signal processing by acquisition cards included in the measurement data acquisition station (incorporating the errors in the thermocouple card and in the station with 16-bit analogue-to-digital converter) and the thermocouple sensor errors. The absolute thermocouple sensor errors result from the error in thermocouple calibration and the error in the measurement with a thermocouple. After calculations, the error resulting from signal processing by acquisition cards included in the measurement data acquisition station amounting to 69.974 μV was obtained. In addition, the following results were calculated: the error in thermocouple calibration—6.582 μV, the error in the measurement using the thermocouple—0.763 μV and then thermocouple sensor errors—6.626 μV. Subsequent calculations led to ΔT L  = 70.287 μV. On the basis of thermocouple temperature measurement range (type K thermocouple, measurement range up to 1,100 °C), and in the temperature range of the thermocouple card (from 0 to 100 mV) 1 K was obtained, corresponding to 90.91 μV. Therefore, ΔT L corresponds to the error in temperature measurement ΔT L  = 0.77 K.

Sample results of calculations in the error analysis for the conducted experiment are as follows: P = 115 calibration points: Δhue = 1.45; SEE = 0.13 K and ΔT L  = 0.77 K [1]. After calculations according to formula (1), Δσ = 0.86 K.

3 Void fraction determination

3.1 Visualisation of two phase flow structures

The analyses of the flow structure were based on the monochrome images of flow structures with an SLR camera of heating foil, obtained on the side contacting fluid flowing in a minichannel. They were processed using Corel graphics software. After the photos had been binarized, the analysis of phase volumes was developed using special software—Techsystem Globe. The software allowed the determination of the areas of the two phases and/or percentage of the defined phase. Methodology of the conversion of greyscale image into monochrome image is presented in detail in [9]. In evaluation, the absolute error of the void fraction was assumed to be equal to the area (point) comprising 0.0064 mm2; it results from the resolution of the image taken by a digital camera [4, 9].

3.2 Void fraction determination methodology

Four initial settings (from #1 up to #4, Fig. 3) for increasing heat flux supplied to the heating surface of the foil were selected for analysis. Figure 4 shows a sample pictures for setting #2 with marked cross-sections (Fig. 4a, b), colour image of cross sections (Fig. 4c), two-phase flow structure images: real (Fig. 4d) and binarized (Fig. 4e). Four cross-sections of the selected images (size 5 mm × 40 mm), were placed at the distance of 90 mm (I), 133 mm (II), 270 mm (III) and 336 mm (IV) from the inlet to the minichannel. The void fraction was determined according to the following formula [1–5]:

$${\varphi } = \frac{{V_{v} }}{{V_{L} + V_{v} }} = \frac{{A_{v} \,\updelta_{M} }}{{(A_{L} + A_{v} )\,\updelta_{M} }} = \frac{{A_{v} }}{{A_{L} + A_{v} }}$$
(3)

where: V—volume, A—cross section area, δ—depth.

Fig. 4
figure 4

Selected images for setting #2: (a) colour image of the heating foil, (b) greyscale image of flow structure image, (c, d, e) images of cross sections: colour image of the heating foil (c), two-phase flow structure images: real (d) and binarized (e); white colour refers to the vapour, and the black colour represents the liquid

Full size image

In our notation, the subscripts referring to the glass pane, the heating foil, the liquid, the vapour and the minichannel are denoted with letters: G, F, L, v and M, respectively.

Liquid and vapour cross-section areas were obtained from phase image analysis performed by means of Techsystem Globe software. The results are presented in the Fig. 5 as void fraction dependence along the minichannel length.

Fig. 5
figure 5

Void fraction dependence along the minichannel length for selected cross sections for settings from #1 up to #4, parameters as for Fig. 3

Full size image

4 Mathematical model

4.1 Problem formulation

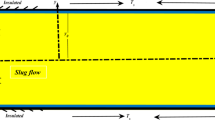
In the mathematical model the investigations took into account the dimension along the flow direction (x), but the dimension perpendicular to it (y) was related to the test section composed of the glass pane, heating foil and minichannel with cooling liquid. Further considerations are focused on the central part of the minichannel (along its length) so that the physical phenomena occurring on outer sides of the minichannel have no influence on thermodynamical parameters in the region studied.

Subcooling liquid at a temperature lower than the saturation temperature enters the minichannel and it is heated by the heating foil during its flow. We assume for both stationary and laminar flows (Re = 880) that velocity vector is parallel to the minichannel length so it has only one non-zero component u = u(y). The component u(y) is approximated by the following roof function:

$$u\left( y \right) = \frac{{u_{max} }}{{\updelta_{M} }}\left( {\updelta_{M} - \left| {2y -\updelta_{M} } \right|} \right)$$
(4)

where u max is equal to the doubled average velocity. The energy equation, exclusively for the liquid phase, has the following form:

$$\nabla^{2} T_{L} = \frac{{c_{L} \,\rho_{L} }}{{\lambda_{L} }}u\left( y \right)\,\frac{{\partial T_{L} }}{\partial x}$$
(5)

where: \(\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}\), c—specific heat, ρ—density, λ—thermal conductivity.

The following boundary conditions were specified for the Eq. (5):

temperature of the liquid in the inlet and outlet of the minichannel equals T in and T out , respectively, i.e.

$$T_{L} \left( {0, y} \right) = T_{in} \quad {\text{for }}0 \le y \le\updelta_{M}$$
(6)
$$T_{L} \left( {L, y} \right) = T_{out} \quad {\text{for }}0 \le y \le\updelta_{M}$$
(7)

temperature of the liquid and the foil at the interface are equal:

$$T_{L} \left( {x,0} \right) = \left\{ {\begin{array}{*{20}l} {T_{F} \left( {x,0} \right),} & {{\text{if}}\quad T_{F} (x,0) < T_{sat} \left( x \right)} \\ {T_{sat} \left( x \right),} & {{\text{if}}\quad T_{F} (x,0) \ge T_{sat} \left( x \right)} \\ \end{array} } \right.\quad {\text{for }}0 \le x \le L$$
(8)

where T sat is the saturation temperature dependent on the pressure, which changes linearly along the minichannel;

the two-phase mixture per unit volume in minichannel contains vapour phase and liquid phase in proportion φ and (1 − φ), respectively. We assumed that the same proportion of vapour and liquid phases refers to any cross-sectional area of the minichannel and then to the heat exchange surface [10]. Hence, all heat generated by the heating foil is transferred to liquid phase proportionally to the void fraction

$$\lambda_{L} \frac{{\partial T_{L} }}{\partial y} = \lambda_{F} \left( {1 - \varphi \left( x \right)} \right)\frac{{\partial T_{F} }}{\partial y}\quad {\text{for}}\quad y = 0\quad {\text{ and}}\quad \, 0 \le x \le L$$
(9)

Stationary heat transfer in the glass pane and heating foil can be described by the following differential equations:

$$\left( {\text{a}} \right)\quad {\text{ for glass}}\,\nabla^{2} T_{G} = 0 \, \quad \left( {\text{b}} \right)\quad {\text{ for foil}}\quad \nabla^{2} T_{F} = - \frac{{q_{V} }}{{\lambda_{F} }}$$
(10)

where q V means volumetric heat flux. For these equations we assume following boundary conditions at the foil-glass interface:

$$T_{F} \left( {x_{i} , -\updelta_{F} } \right) = T_{G} \left( {x_{i} , -\updelta_{F} } \right) = T_{i}$$
(11)
$$\lambda_{F} \frac{{\partial T_{F} }}{\partial y} = \lambda_{G} \frac{{\partial T_{G} }}{\partial y}\quad {\text{for}}\,y = -\updelta_{F} \quad {\text{and}}\quad \, 0 \le x \le L$$
(12)

where T i means the measurements obtained with liquid crystal thermography at the foil-glass contact at discrete points (x i  − δ F ). To complete specification of the functions T F and T G we assume that the outer surfaces of the minichannel are thermally isolated. Figure 6 contains the geometry and prescribed conditions of the considered problem.

Fig. 6
figure 6

Diagram of the boiling liquid flow in the minichannel, with the adapted boundary conditions (pictorial view, not to scale)

Full size image

4.2 Trefftz method

Equation (5) subject to prescribed boundary conditions (6)–(9) will be solved by the Trefftz method [6, 10, 11]. In this method the unknown solution of a differential equation is approximated with a linear combination of the functions (so called Trefftz functions) which satisfy the governing equation. The unknown coefficients are determined by matching the boundary conditions. Before numerical calculations we have to generate Trefftz functions corresponding to Eq. (5) with roof-shaped velocity of the liquid, u(y). The unknown solution to Eq. (5) is expanded in Taylor series, around the point (0.0):

$$\begin{aligned} & T_{L} \left( {x,y} \right) = T_{L} \left( {0,0} \right) + \frac{{\partial T_{L} }}{\partial x}x + \frac{{\partial T_{L} }}{\partial y}y + \frac{1}{2!}\frac{{\partial^{2} T_{L} }}{{\partial x^{2} }}x^{2} \\ & \quad + \frac{2}{2!}\frac{{\partial^{2} T_{L} }}{\partial x\partial y}xy + \frac{1}{2!}\frac{{\partial^{2} T_{L} }}{{\partial y^{2} }}y^{2} + \frac{1}{3!}\frac{{\partial^{3} T_{L} }}{{\partial x^{3} }}x^{3} + \ldots \\ \end{aligned}$$
(13)

From Eq. (5) we get the dependence concerning the second partial derivative \(\frac{{\partial^{2} T_{L} }}{{\partial y^{2} }}\)

$$\frac{{\partial^{2} T_{L} }}{{\partial y^{2} }} = \frac{{c_{L} \,\rho_{L} }}{{\lambda_{L} }}u\left( y \right)\,\frac{{\partial T_{L} }}{\partial x} - \frac{{\partial^{2} T_{L} }}{{\partial x^{2} }}$$
(14)

which we substitute into Eq. (13) and after some algebraic manipulations the unknown solution T L has the following representation

$$T_{L} \left( {x,y} \right) = \sum\limits_{n = 1}^{\infty } {b_{n} v_{n} \left( {x,y} \right)}$$
(15)

where polynomials v n (x, y) are the desired Trefftz functions satisfying the energy Eq. (5) exactly.

Next, we approximate the solution T L with finitely many v n (x, y)’s which gives

$$T_{L} \left( {x,y} \right) \approx \sum\limits_{n = 1}^{N} {b_{n} v_{n} \left( {x,y} \right)}$$
(16)

The unknown coefficients of this expansion, b n will be selected to make the approximant T L best match (in variational sense) the boundary conditions (6)–(9). In terms of computations, by proper choice of b n ’s one should minimize the functional J that describes mean square error between function T L and prescribed boundary condition (6)–(9). The functional has the following form

$$\begin{aligned} & J = \int\limits_{0}^{{\updelta_{M} }} {\left( {\sum\limits_{n = 1}^{N} {b_{n} v_{n} \left( {0,y} \right) - T_{in} } } \right)^{2} dy + \int\limits_{0}^{{\updelta_{M} }} {\left( {\sum\limits_{n = 1}^{N} {b_{n} v_{n} \left( {L,y} \right) - T_{out} } } \right)^{2} dy } } \\ & \quad + \int\limits_{0}^{L} {\left( {\sum\limits_{n = 1}^{N} {\lambda_{L} b_{n} \frac{{\partial v_{n} \left( {x,0} \right)}}{\partial y} - \lambda_{F} \left( {1 - \varphi \left( x \right)} \right)\frac{{\partial T_{F} \left( {x,0} \right)}}{\partial y}} } \right)^{2} dx + } \int\limits_{0}^{L} {\left( {\sum\limits_{n = 1}^{N} {b_{n} v_{n} \left( {x,0} \right) - T_{L} \left( {x,0} \right)} } \right)^{2} dx} \\ \end{aligned}$$
(17)

Finally we get the solution T L which satisfies the energy Eq. (5) exactly and the boundary conditions approximately. In the like manner we can obtain the solutions of Eqs. (10a and b) using Trefftz functions (harmonic polynomials) suitable for Laplace Eq. [11]. Trefftz method allows to determine two-dimensional distributions of temperature in the foil and in the glass as well as their gradients along the minichannel.

5 Equalizing calculus

Application of equalizing calculus means a choice of such corrections ɛ i for measurements T i that for the corrected measurements T corr i the following condition is satisfied

$$T_{i}^{corr} = T_{i} + \varepsilon_{i}$$
(18)

Corrections ɛ i have normal distribution with the mean value equal to zero and finite variance equal to σ 2 i , [12, 13], where errors σ i are defined by the Eq. (1). For P of independent measurements the density function for corrected measurement results T corr1 , T corr2 ,…, T corr P (and whereby corrections ɛ 1,ɛ 2,…,ɛ P ) is delineated as the product of the density function for normal distribution i.e.

$$\Phi \left( {\upvarepsilon_{1} ,\upvarepsilon_{2} , \ldots ,\upvarepsilon_{P} } \right) = \frac{1}{{\left( {2\uppi} \right)^{0.5P} \left( {\upsigma_{1}\upsigma_{2} \ldots\upsigma_{P} } \right)}}\exp \left[ { - \frac{1}{2}\sum\limits_{i = 1}^{P} {\left( {\frac{{\upvarepsilon_{i} }}{{\upsigma_{i} }}} \right)^{2} } } \right]$$
(19)

Function Φ is called the likelihood function. Determination of corrections ɛ i leads to the determination of the maximum for likelihood function Φ. Corrections determined by this method are always compliant and asymptotically efficient, i.e. when P increases, the estimation result approaches the real value, whilst estimation variance will be as low as possible.

Function Φ is the highest when \(\sum\limits_{i = 1}^{P} {\left( {\frac{{\upvarepsilon_{i} }}{{\upsigma_{i} }}} \right)^{2} } \to\) min. If this is the case (when ɛ i have assumed normal distribution) the maximum likehood function method leads to the same results as the method of least squares. When applying the eqaulizing calculus in Trefftz method, the corrected value of foil temperature T corr F should be determined to meet the following condition:

$$T_{F}^{corr} \left( {x_{i} ,\updelta_{G} } \right) - T_{i}^{corr} = 0$$
(20)

The determination of the maximum of the likehood function Φ, Eq. (19), assuming condition (20), leads to the minimalization of the Lagrange function:

$$\Omega = \sum\limits_{i = 1}^{P} {\left( {\frac{{\upvarepsilon_{i}^{{}} }}{{\upsigma_{i}^{{}} }}} \right)^{2} } + 2\sum\limits_{i = 1}^{P} {\upomega_{i} \left( {T_{F}^{corr} \left( {x_{i} ,\updelta_{G} } \right) - T_{i}^{corr} } \right)} \to \hbox{min}$$
(21)

where ω i were Lagrange multipliers.

Having corrected temperature measurements, we recalculated measurement errors σ corr i according to the error propagation law [12, 13]. As expected, equalizing calculus smoothed the measurement data and reduced the errors, see Fig. 8. Owing to known values of T corr i , it was possible to recalculate approximated temperatures of glass, foil (as described in [6]) and liquid, denoted T corr G , T corr F and T corr L , respectively.

6 Results

Numerical calculations were performed for experimental data and they concerned forced flow of the cooling liquid FC-72 through asymmetrically heated vertical minichannel. Calculations were conducted for settings from #1 up to #4, with all parameters of the experiment given in Fig. 3. Settings #1 and #2 apply to boiling incipience, setting #3 covers the interim status; setting #4 applies to the developed boiling. The void fraction described in detail in 2.2 and refereed to the settings under consideration, was approximated with a third degree polynomial as shown in Fig. 5.

At first, corrected measurements T corr i were determined using equalizing calculus, Fig. 8b. Sample results obtained for setting #4 are presented in Fig. 7a. Using the equalizing calculus, on the basis of the error propagation, law corrected errors σ corr i were computed; their values are considerably lower than errors σ i calculated from (1), Fig. 7b.

Fig. 7
figure 7

a Temperature measurements T i and corrected measurements T corr i ; b measurement errors σ i and corrected measurement errors σ corr i , data for setting #4

Full size image

Then computations involved the use of Trefftz method for finding two-dimensional temperature distribution in the glass pane and the heating foil. In the next step temperatures were calculated in the liquid phase. We designed approximate temperature distributions T corr G , T corr F and T corr L to be polynomials of the same degree. Fig. 8a presents two-dimensional temperature distribution in the heating foil and the glass pane, both obtained by Trefftz method for corrected measurements T corr i . Either of the approximants satisfies the assumed conditions (11) and (12), with a relatively high accuracy, Fig. 8b. Similarly, Fig. 9a and Fig 10a shows temperature field in the heating foil and the flowing liquid. Figure 9 applies to the case when boiling incipience occurs (data for setting #1), whilst Fig. 10 reflects the situation when developed boiling takes place (data for setting #4). One can notice the characteristic shape of isotherms in the liquid (see Figs. 9a, 10a) which is due to modelling the velocity vector as a roof function. In Figs. 9b and 10b temperatures of the heating foil and the liquid at the foil-liquid interface are compared to saturation temperature. In [10] similar research, assuming a parabolic liquid velocity profile, was conducted for bubbly and bubbly–slug flow.

Fig. 8
figure 8

a Two dimension temperature distributions of the glass pane and the heating foil, both obtained with Trefftz method for corrected measurements, b corrected temperatures of the corrected measurements (green), glass pane (red) and foil (blue) at the glass-foil contact, data for settings #1 and #4 (colour figure online)

Full size image
Fig. 9
figure 9

a Two dimension temperature distributions of the heating foil and of the liquid, both obtained with Trefftz method, b corrected temperatures of the foil (blue), of the liquid (red) and saturation (green) at the foilliquid contact as a function of distance from the inlet to the channel. Setting #1 (colour figure online)

Full size image
Fig. 10
figure 10

a Two dimension temperature distributions of the heating foil and of the liquid, both obtained with Trefftz method, b corrected temperatures of the foil (blue), of the liquid (red) and saturation (green) at the foilliquid contact as a function of distance from the inlet to the channel. Setting #4 (colour figure online)

Full size image

The known liquid and foil temperature distributions allowed calculating heat transfer coefficient α at the foil-glass contact points from the Robin boundary condition [14].

$$- \lambda_{F} \frac{{\partial \, T_{F}^{corr} (x,0)}}{\partial \, y} = \alpha \left( x \right)\,\left( {T_{F}^{corr} (x,0) - T_{ave} (x)} \right) .$$
(22)

Two options for computing liquid temperature were considered. In the first approach the averaged temperature across the whole width of the minichannel were assumed as reference temperature T ave , Eq. (23a). Since the liquid reaches its maximal velocity along the axis of the minichannel, Eq. (2), in the second approach we took average temperature at points from x = 0 to x = 0.5δ M as reference temperature T ave , Eq. (23b).

$$\left( {\text{a}} \right)\quad T1_{ave} \left( x \right) = \frac{1}{{\updelta_{M} }}\int\limits_{0}^{{\updelta_{M} }} {T_{L}^{corr} \left( {x,y} \right)dy} \quad \left( {\text{b}} \right)\quad T2_{ave} \left( x \right) = \frac{1}{{0.5\,\updelta_{M} }}\int\limits_{0}^{{0.5\,\updelta_{M} }} {T_{L}^{corr} \left( {x,y} \right)dy}$$
(23)

In the minichannel flow boiling, considerable heat transfer enhancement takes place at boiling incipience. It is observed as a sharp increase in the heat transfer coefficient at the foil-liquid contact, Fig. 11c. Similar results in flow boiling incipience were obtained in the study [4]. In the case of developed boiling, the heat transfer coefficient decreases as the void fraction increases. As far as the transition flow was concerned, the increase in the heat transfer coefficient was observed. For higher shares of the vapour phase in the two-phase mixture, heat transfer coefficient values will decrease.

Fig. 11
figure 11

Heat transfer coefficient as a function of distance from the inlet to the minichannel determined in the reference temperature: a from Eq. (23a), b from Eq. (23b)

Full size image

7 Conclusions

The paper presents the approach to modelling laminar flow of the fluid during boiling incipience and developed boiling. When a mathematical model was formulated then the Trefftz method was used in order to solve it, however the validity of the solution is restricted to liquid phase only.

Special Trefftz functions had to be generated for the case of roof-shaped velocity of the liquid.

The proposed method based on Trefftz functions was successfully applied to the direct problem of finding temperature distribution in the glass pane. Moreover, this method turned to be suitable for the considered inverse problems: in the heating foil were we had a specified condition at one boundary and in the liquid where we assumed convective boundary condition in order to compute the heat transfer coefficient. The obtained numerical results show high compliance with physical assumptions of the model and have satisfactory accuracy.

Equilizing calculus applied to Trefftz method helped smooth the measurement data and reduce their errors.

In the minichannel flow boiling, considerable heat transfer enhancement takes place at boiling incipience. In the case of developed boiling, the heat transfer coefficient decreases as the void fraction increases. As far as the transition flow was concerned, the increase in the heat transfer coefficient was observed, but the data concerned a small range of the void fraction. For higher shares of the vapour phase in the two-phase mixture, heat transfer coefficient values will decrease. There are plans for in-depth exploring transition and developed boiling area and future verification of the data.

Since the results based on Trefftz method turned to be promising, further research will be devoted to adapting the method to finding temperature distribution in the fluid which would include vapour phase as well as liquid phase.