Abstract
A key open problem in M-theory is the identification of the degrees of freedom that are expected to be hidden at ADE-singularities in spacetime. Comparison with the classification of D-branes by K-theory suggests that the answer must come from the right choice of generalized cohomology theory for M-branes. Here we show that real equivariant Cohomotopy on superspaces is a consistent such choice, at least rationally. After explaining this new approach, we demonstrate how to use Elmendorf’s Theorem in equivariant homotopy theory to reveal ADE-singularities as part of the data of equivariant \(S^{4}\)-valued super-cocycles on 11d super-spacetime. We classify these super-cocycles and find a detailed black brane scan that enhances the entries of the old brane scan to cascades of fundamental brane super-cocycles on strata of intersecting black M-brane species. We find that on each singular stratum the black brane’s instanton contribution, namely its super Nambu–Goto/Green–Schwarz action, appears as the homotopy datum associated to the morphisms in the orbit category.



Similar content being viewed by others
Notes
From [Klein1872, Sec. 1]: “As a generalization of geometry arises then the following comprehensive problem: given a manifoldness and a group of transformations of the same; to investigate the configurations belonging to the manifoldness with regard to such properties as are not altered by the transformations of the group”.
While such a derivation of K-theory from M-theory is suggested by the title of [DMW03], that article only checks that the behavior of the partition function of the 11d supergravity C-field is compatible with the a priori K-theory classification of D-branes.
It may be worthwhile to recall that, in mathematics, it is not unusual to postulate the existence of certain theories before one actually knows about their nature. Famous historical examples include the theory of motives or the theory of the field with one element. The former has meanwhile been found.
[HW95, p. 1]: “As it has been proposed that [this] theory is a supermembrane theory but there are some reasons to doubt that interpretation, we will non-committedly call it theM-theory, leaving to the future the relation ofMto membranes.”
[Wi95c, p. 2]: “Mstands for magic, mystery, or membrane, according to taste.”
[Wi03]: “Back in the early ’70s, the Italian physicist, Daniele Amati reportedly said that string theory was part of 21st-century physics that fell by chance into the 20th century. I think it was a very wise remark. How wise it was is so clear from the fact that 30 years later we’re still trying to understand what string theory really is.”
In [Sor99, Sor01] it is shown that the traditional derivation of the Green–Schwarz-type sigma-models (3), is clarified drastically if one takes the worldvolume \(\Sigma _{p+1}\) (1) to be a supermanifold locally modeled on the relevant BPS super subspace \(\mathbb {R}^{p,1\mathbf {N}} \hookrightarrow \mathbb {R}^{10,1\vert \mathbf {32}}\). This is exactly what we see appear in Theorem 6.1, via Proposition 6.11.
In the sprit of this physics section, we are deliberately suppressing notation for pullback of differential forms in these expressions, in order to bring out conceptual meaning of these formulas; see instead Sect. 6.2 for precise details.
The cells in a cell complex are the spatial analogues of algebra generators in an algebra.
If there are different real representations of the same real dimension we will distinguish them by extra decoration of their dimension in boldface, for instance \(\mathbf {N}\) and \(\overline{\mathbf {N}}\).
This follows by representing fibrant resolutions in terms of homotopies, as in Example 3.27, in particular (29), (30).
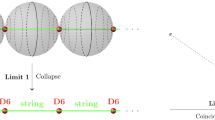
The discussion in [MdF09, Sec. 8.3] is motivated by classifying supersymmetric supergravity solutions corresponding to the near horizon limit of black M5 branes, but ends up classifying fixed loci \(\mathbb {R}^{6,1} \hookrightarrow \mathbb {R}^{10,1}\) corresponding to 6-branes, as in the above statement. In physics lingo, this reflects the phenomenon that multiple D6-branes end pairwise on NS5-branes. We discussed this subtle point in the physics interpretation in Sect. 2.2.
This just reflects the fact that a map from one disjoint union of connected spaces to another is simply a tuple of maps between connected spaces, one from each connected component of the domain to a connected component of the codomain.
References
Acharya, B.: M Theory, \(G_2\)-manifolds and four dimensional physics. Class. Quantum Gravity 19, 5619–5653 (2002). http://users.ictp.it/~pub_off/lectures/lns013/Acharya/Acharya_Final.pdf
Acharya, B.S., Figueroa-O’Farrill, J.M., Hull, C.M., Spence, B.: Branes at conical singularities and holography. Adv. Theor. Math. Phys. 2, 1249–1286 (1999). arXiv:hep-th/9808014
Acharya, B., Gukov, S.: M theory and singularities of exceptional holonomy manifolds. Phys. Rep. 392, 121–189 (2004). arXiv:hep-th/0409191
Acharya, B., Witten, E.: Chiral fermions from manifolds of \(G_2\)-holonomy. arXiv:hep-th/0109152
Achúcarro, A., Evans, J., Townsend, P., Wiltshire, D.: Super \(p\)-branes. Phys. Lett. B 198, 441–446 (1987). spire:22286
Allday, C., Puppe, V.: Cohomological Methods in Transformation Groups. Cambridge University Press, Cambridge (1993)
Atiyah, M.: K-theory and reality. Q. J. Math. 17(1), 367–386 (1966)
Atiyah, M., Witten, E.: M-theory dynamics on a manifold of \(G_2\) holonomy. Adv. Theor. Math. Phys. 6, 1–106 (2003). arXiv:hep-th/0107177
de Azcárraga, J., Townsend, P.: Superspace geometry and the classification of supersymmetric extended objects. Phy. Rev. Lett. 62, 2579–2582 (1989). spire:284635
Baez, J., Huerta, J.: Division algebras and supersymmetry I. In: Doran, R., Friedman, G., Rosenberg J. (eds.), Superstrings, Geometry, Topology, and \(C^{\ast }\)-algebras, Proceedings of Symposia in Pure Mathematics 81, AMS, Providence, (2010), pp. 65–80. arXiv:0909.0551
Baez, J., Huerta, J.: Division algebras and supersymmetry II. Adv. Math. Theor. Phys. 15, 1373–1410 (2011). arXiv:1003.3436
Bagger, J., Lambert, N., Mukhi, S., Papageorgakis, C.: Multiple membranes in M-theory. Phys. Rep. 527, 1–100 (2013). arXiv:1203.3546
Bär, C.: Real killing spinors and holonomy. Commun. Math. Phys. 154, 509–521 (1993)
Becker, K., Becker, M., Schwarz, J.: String Theory and M-Theory: A Modern Introduction. Cambridge University Press, Cambridge (2006)
Becker, K., Becker, M., Strominger, A.: Fivebranes, membranes and non-perturbative string theory. Nucl. Phys. B456, 130–152 (1995). arXiv:hep-th/9507158
Bergshoeff, E., van der Schaar, J.P.: On M-9-branes. Class. Quantum Gravity 16, 23–39 (1999). arXiv:hep-th/9806069
Berkooz, M.: A supergravity dual of a \((1,0)\) field theory in six dimensions. Phys. Lett. B437, 315–317 (1998). arXiv:hep-th/9802195
Berman, D., Perry, M., Sezgin, E., Thompson, D.: Boundary conditions for interacting membranes. J. High Energy Phys. 1004, 025 (2010). arXiv:0912.3504
Borceux, F.: Basic Category Theory. Handbook of Categorical Algebra, vol. 1. Cambirdge University Press, Cambirdge (1995)
Bergshoeff, E., Sezgin, E., Townsend, P.K.: Supermembranes and eleven-dimensional supergravity. Phys. Lett. B189, 75–78 (1987)
Bousfield, A., Guggenheim, V.: On PL deRham theory and rational homotopy type. Memoirs of the AMS 179 (1976)
Braunack-Mayer, V.: Rational parameterized stable homotopy theory, PhD thesis, Zurich University (2018). https://ncatlab.org/schreiber/show/thesis+Braunack-Mayer
Blencowe, M.P., Duff, M.: Supersingletons. Phys. Lett. B 203, 229–236 (1988). spire:252628
Blumberg, A.: Equivariant homotopy theory, lecture notes (2017). github.com/adebray/equivariant_homotopy_theory
Braunack-Mayer, V., Sati, H., Schreiber, U.: Gauge enhancement for Super M-branes via Parameterized stable homotopy theory. Commun. Math. Phys. (2019). arXiv:1805.05987 [hep-th]
Bredon, G.: Equivariant cohomology theories, Springer Lecture Notes in Mathematics Vol. 34 (1967)
Bredon, G.E.: Introduction to Compact Transformation Groups. Academic Press, New York (1972)
Brodie, J., Hanany, A.: Type IIA superstrings, chiral symmetry, and \(N=1\) 4D gauge theory dualities. Nucl. Phys. B506, 157–182 (1997)
Čap, A., Slovák, J.: Parabolic Geometries I: Background and General Theory, Mathematical Surveys and Monomgraphs, Volume 154, American Mathematical Society (2009)
Candiello, A., Lechner, K.: Duality in supergravity theories. Nucl. Phys. B412, 479–501 (1994). arXiv:hep-th/9309143
Cartan, É.: Sur les variétés à connexion affine et la théorie de la relativité généralisée (première partie) Ann. scient. de l’Ecole Normale Supérieure, Sér. 3, 40, 325–412 (1923). http://www.numdam.org/item?id=ASENS_1923_3_40__325_0
Castellani, L., D’Auria, R., Fré, P.: Supergravity and Superstrings—A Geometric Perspective. World Scientific, Singapore (1991)
Clay Mathematics Institute: Millenium Problems—YangMills and Mass Gap. www.claymath.org/millennium-problems/yang-mills-and-mass-gap
Conner, P.E., Floyd, E.E.: On the construction of periodic maps without fixed points. Proc. Am. Math. Soc. 10, 354–360 (1959)
Dasgupta, A., Nicolai, H., Plefka, J.: An Introduction to the Quantum Supermembrane, Grav. Cosmol. 8, 1 (2002); Rev. Mex. Fis. 49(S1), 1–10 (2003). arXiv:hep-th/0201182
de Medeiros, P., Figueroa-O’Farrill, J., Gadhia, S., Méndez-Escobar, E.: Half-BPS quotients in M-theory: ADE with a twist. J. High Energy Phys. 0910, 038 (2009). arXiv:0909.0163
de Medeiros, P., Figueroa-O’Farrill, J.: Half-BPS M2-brane orbifolds. Adv. Theor. Math. Phys. 16, 1349–1408 (2012). arXiv:1007.4761
de Wit, B., Hoppe, J., Nicolai, H.: On the quantum mechanics of supermembranes. Nucl. Phys. B305, 545–581 (1988)
Del Zotto, M., Heckman, J., Tomasiello, A., Vafa, C.: 6d conformal matter. J. High Energy Phys. 2015, 54 (2015). arXiv:1407.6359
Deligne, P., Freed, D.: Sign manifesto publications.ias.edu/sites/default/files/79_SignManifesto.pdf, in Supersolutions arXiv:hep-th/9901094. In: Deligne, P. et. al. (eds.) Quantum Fields and Strings, A course for mathematicians, AMS (1999)
Diaconescu, D., Moore, G., Witten, E.: \(E_8\)-gauge theory and a derivation of K-theory from M-theory. Adv. Theor. Math. Phys. 6, 1031 (2003). arXiv:hep-th/0005090
Distler, J., Freed, D., Moore, G.: Orientifold Précis In: Sati, H., Schreiber, U. (eds.), Mathematical Foundations of Quantum Field and Perturbative String Theory, Proceedings of Symposia in Pure Mathematics, AMS (2011) arXiv:0906.0795. https://ncatlab.org/nlab/files/FreedESI2012.pdf
Doran, C., Mendez-Diez, S., Rosenberg, J.: T-duality for orientifolds and twisted KR-theory. Lett. Math. Phys. 104(11), 1333–1364 (2014). arXiv:1306.1779
Duff, M.: Supermembranes: the first fifteen weeks. Class. Quantum Gravity 5, 189–205 (1988). spire:248034
Duff, M.: Anti-de Sitter space, branes, singletons, superconformal field theories and all that. Int. J. Mod. Phys. A14, 815–844 (1999). [arXiv:hep-th/9808100]
Duff, M.: TASI Lectures on Branes, Black Holes and Anti-de Sitter Space. arXiv:hep-th/9912164
Duff, M. (ed.): The World in Eleven Dimensions: Supergravity. Supermembranes and M-Theory. IoP, Bristol (1999)
Duff, M.: Near-horizon brane-scan revived. Nucl. Phys. B810, 193–209 (2009). arXiv:0804.3675
Duff, M., Inami, T., Pope, C., Sezgin, E., Stelle, K.: Semiclassical quantization of the supermembrane. Nucl. Phys. B297, 515–538 (1988). spire:247064
Duff, M., Khuri, R., Lu, J.X.: String solitons. Phys. Rep. 259, 213–326 (1995). arXiv:hep-th/9412184
Duff, M., Lu, J.: Black and super \(p\)-branes in diverse dimensions. Nucl. Phys. B416, 301–334 (1994). arXiv:hep-th/9306052
Duff, M., Sutton, C.: The membrane at the end of the universe. New Sci. 118, 67–71 (1988)
Duff, M., Howe, P., Inami, T., Stelle, K.: Superstrings in \(D =10\) from Supermembranes in \(D =11\). Phys. Lett. B191, 70–74 (1987). reprinted in [Du99] spire:245249
Duff, M.J., Lu, J.X.: Type II p-branes: the brane-scan revisited. Nucl. Phys. B390, 276–290 (1993). arXiv:hep-th/9207060
P. du Val, On isolated singularities of surfaces which do not affect the conditions of adjunction, I, II and III, Proc. Camb. Phil. Soc. 30 1934, 453–459, 460–465, 483–491
Egeileh, M., El Chami, F.: Some remarks on the geometry of superspace supergravity. J. Geom. Phys. 62, 53–60 (2012)
Elitzur, S., Giveon, A., Kutasov, D., Rabinovici, E., Sarkissian, G.: D-branes in the background of NS fivebranes. J. High Energy Phys. 0008, 046 (2000). arXiv:hep-th/0005052
Elmendorf, A.: Systems of fixed point sets. Trans. Am. Math. Soc. 277, 275–284 (1983)
Epstein, H., Glaser, V.: The Role of locality in perturbation theory. Annales Poincaré Phys. Theor. A 19, 211 (1973). http://www.numdam.org/item?id=AIHPA_1973__19_3_211_0
Evslin, J.: What Does(n’t) K-theory Classify?, Second Modave Summer School in Mathematical Physics. arXiv:hep-th/0610328
Evslin, J., Sati, H.: Can D-branes wrap nonrepresentable cycles? J. High Energy Phys. 0610, 050 (2006). arXiv:hep-th/0607045
Fazzi, M.: Higher-dimensional field theories from type II supergravity. arXiv:1712.04447
Figueroa-O’Farrill, J.: Majorana spinors. http://www.maths.ed.ac.uk/~jmf/Teaching/Lectures/Majorana.pdf
Figueroa-O’Farrill, J.: Near-horizon geometries of supersymmetric branes, talk at SUSY98. arXiv:hep-th/9807149
Figueroa-O’Farrill, J., Santi, A.: Spencer cohomology and eleven-dimensional supergravity. Commun. Math. Phys. 349, 627–660 (2017). arXiv:1511.08737 [hep-th]
Fiorenza, D., Sati, H., Schreiber, U.: Multiple M5-branes, string 2-connections, and 7d nonabelian Chern-Simons theory. Adv. Theor. Math. Phys. 18, 229–321 (2014). arXiv:1201.5277
Fiorenza, D., Sati, H., Schreiber, U.: Super Lie \(n\)-algebra extensions, higher WZW models, and super \(p\)-branes with tensor multiplet fields. Int. J. Geom. Methods Mod. Phys. 12, 1550018 (2015). arXiv:1308.5264
Fiorenza, D., Sati, H., Schreiber, U.: Rational sphere valued supercocycles in M-theory and type IIA string theory. J. Geom. Phys. 114, 91–108 (2017). arXiv:1606.03206
Fiorenza, D., Sati, H., Schreiber, U.: The WZW term of the M5-brane and differential cohomotopy. J. Math. Phys. 56, 102301 (2015). arXiv:1506.07557
Fiorenza, D., Sati, H., Schreiber, U.: T-Duality from super Lie \(n\)-algebra cocycles for super p-branes. Adv. Theor. Math. Phys. 22(5), (2018). arXiv:1611.06536
Fiorenza, D., Sati, H., Schreiber, U.: T-duality in rational homotopy theory via \(L_{\infty }\)-algebras, Geom. Topol. Math. Phys. 1, (2018), special volume in tribute of Jim Stasheff and Dennis Sullivan. arXiv:1712.00758 [math-ph]
Fiorenza, D., Sati, H., Schreiber, U.: Higher T-duality of M-branes. arXiv:1803.05634
Fiorenza, D., Sati, H., Schreiber, U.: The rational higher structure of M-theory, Proceedings of Higher Structures in M-Theory, Durham Symposium 2018, Fortsch. Phys. (2019)
Freed, D.: Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry, Int. Press, Somerville, MA, pp. 129–194 (2000) arXiv:hep-th/0011220
Freed, D., Witten, E.: Anomalies in string theory with D-branes. Asian J. Math. 3, 819–852 (1999). arXiv:hep-th/9907189
Gauntlett, J.: Intersecting Branes, in Dualities in Gauge and String Theories, Proc. APCTP Winter School “Dualities of Gauge and String Theories”, Korea (1997). arXiv:hep-th/9705011
Gorbatov, E., Kaplunovsky, V.S., Sonnenschein, J., Theisen, S., Yankielowicz, S.: On heterotic orbifolds, M theory and type I’ brane engineering. J. High Energy Phys. 0205, 015 (2002). arXiv:hep-th/0108135
Grady, D., Sati, H.: Twisted differential generalized cohomology theories and their Atiyah-Hirzebruch spectral sequence, to appear in Alg. Geom. Top. arXiv:1711.06650 [math.AT]
Grady, D., Sati, H.: Differential KO-theory: constructions, computations, and applications, [arXiv:1809.07059] [math.AT]
Grady, D., Sati, H.: Ramond-Ramond fields and twisted differential K-theory, preprint
Gueven, R.: Black \(p\)-brane solutions of \(D = 11\) supergravity theory. Phys. Lett. B276, 49–55 (1992). (reprinted in [Du99B]) spire:338203
Guillemin, V.: The integrability problem for \(G\)-structures. Trans. Am. Math. Soc. 116, 544–560 (1965). jstor:1994134
Gukov, S.: K-theory, reality, and orientifolds. Commun. Math. Phys. 210, 621–639 (2000). arXiv:hep-th/9901042
Haghighat, B., Iqbal, A., Kozcaz, C., Lockhart, G., Vafa, C.: M-strings. Commun. Math. Phys. 334, 779–842 (2015). arXiv:1305.6322
Han, S.K., Koh, I.G.: \(N=4\) remaining supersymmetry in Kaluza-Klein monopole background in \(\text{ D }=11\) supergravity theory. Phys. Rev. D31, 2503–2506 (1985)
Hanany, A., Kol, B.: On orientifolds, discrete torsion, branes and M theory. J. High Energy Phys. 0006, 013 (2000). arXiv:hep-th/0003025
Harvey, J., Moore, G.: Superpotentials and Membrane Instantons. arXiv:hep-th/9907026
Heckman, J., Morrison, D., Vafa, C.: On the classification of 6D SCFTs and generalized ADE orbifolds. J. High Energ. Phys. 2014, 28 (2014). arXiv:1312.5746
Hess, K.: Rational homotopy theory: a brief introduction, Interactions between homotopy theory and algebra, 175–202. Contemp. Math 436 arXiv:math.AT/0604626
Hill, M.A., Hopkins, M.J., Ravenel, D.C.: On the non-existence of elements of Kervaire invariant one. Ann. Math. 184, 1–262 (2016). arXiv:0908.3724
Hohenegger, S., Iqbal, A.: M-strings, Elliptic Genera and \(N=4\) String Amplitudes. arXiv:1310.1325
Hollands, S., Ishibashi, A.: Black hole uniqueness theorems in higher dimensional spacetimes. Class. Quantum Gravity 29, 163001 (2012). arXiv:1206.1164
Hořava, P., Witten, E.: Heterotic and Type I string dynamics from eleven dimensions. Nucl. Phys. B460, 506–524 (1996). arXiv:hep-th/9510209
Hořava, P., Witten, E.: Eleven dimensional supergravity on a manifold with boundary. Nucl. Phys. B475, 94–114 (1996). arXiv:hep-th/9603142
Hori, K.: Consistency conditions for fivebrane in M theory on \({\mathbb{R}}^5/{\mathbb{Z}}_2\) orbifold. Nucl. Phys. B539, 35–78 (1999). arXiv:hep-th/9805141
Hori, K.: D-branes, T-duality, and index theory. Adv. Theor. Math. Phys. 3, 281–342 (1999). arXiv:hep-th/9902102
Howe, P.: Weyl superspace. Phys. Lett. B 415, 149–155 (1997). arXiv:hep-th/9707184
Hu, P., Kriz, I.: Real-oriented homotopy theory and an analogue of the Adams–Novikov spectral sequence. Topology 40, 317–399 (2001)
Huerta, J., Schreiber, U.: M-theory from the superpoint. Lett. Math. Phys. 108, 2695–2727 (2018). arXiv:1702.01774 [hep-th]
Hull, C.: Exact pp wave solutions of eleven-dimensional supergravity. Phys. Lett. B 139, 39–41 (1984). spire:14499
Ibáñez, L., Uranga, A.: String Theory and Particle Physics: An Introduction to String Phenomenology. Cambridge University Press, Cambridge (2012)
Kashima, K.: The M2-brane solution of heterotic M-theory with the Gauss-Bonnet \(R^{2}\) terms. Prog. Theor. Phys. 105, 301–321 (2001). arXiv:hep-th/0010286
Keenan, A.: Which finite groups act freely on spheres? (2003) www.math.utah.edu/~keenan/actions.pdf
Kim, J., Kim, S., Lee, K., Park, J., Vafa, C.: Elliptic genus of E-strings. J. High Energy Phys. 1709, 098 (2017). arXiv:1411.2324
Klein, F.: Vergleichende Betrachtungen über neuere geometrische Forschungen (1872), translation by Haskell, M.W.: A comparative review of recent researches in geometry. Bull. N. Y. Math. Soc. 2, 215–249 (1892–1893)
Klein, F.: Vorlesungen uber das Ikosaeder und die Auflösung der Gleichungen vom funften Grade, 1884, translated as Lectures on the Icosahedron and the Resolution of Equations of Degree Five by George Morrice (1888). archive.org/details/cu31924059413439
Kriz, I., Sati, H.: Type IIB string theory, S-duality, and generalized cohomology. Nucl. Phys. B715, 639–664 (2005). arXiv:hep-th/0410293
Kugo, T., Townsend, P.: Supersymmetry and the division algebras. Nucl. Phys. B 221, 357–380 (1982). spire:181889
Lalak, Z., Lukas, A., Ovrut, B.: Soliton solutions of M-theory on an orbifold. Phys. Lett. B425, 59–70 (1998). arXiv:hep-th/9709214
Lott, J.: The geometry of supergravity torsion constraints. Commun. Math. Phys. 133, 563–615 (1990). see arXiv:math/0108125
Lurie, J.: Higher Topos Theory, [arXiv:math/0608040], Higher Algebra [www.math.harvard.edu/~lurie/papers/HA.pdf], Spectral Algebraic Geometry. www.math.harvard.edu/~lurie/papers/SAG-rootfile.pdf
Mathai, V., Sati, H.: Some relations between twisted K-theory and \(E_8\) gauge theory. J. High Energy Phys. 03, 016 (2004). arXiv:hep-th/0312033
May, J.P. ed., Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91, Conference Board of the Mathematical Sciences, Washington, DC (1996)
Mazur, P.O.: Black Uniqueness Theorems, In: MacCallum, M.A.H. (ed.) Proceedings of the 11th International Conference on General Relativity and Gravitation, Cambridge University Press, pp. 130–157 (1987). arXiv:hep-th/0101012
Miller, G.A., Blichfeldt, H.F., Dickson, L.E.: Theory and Applications of Finite Groups. Dover, New York (1916)
Moore, G.: Physical Mathematics and the Future, talk at Strings (2014). http://www.physics.rutgers.edu/~gmoore/PhysicalMathematicsAndFuture.pdf
Moore, G., Witten, E.: Self-duality, Ramond–Ramond fields, and K-theory. J. High Energy Phys. 0005, 032 (2000). arXiv:hep-th/9912279
Morrison, D.R., Plesser, M.R.: Non-spherical horizons I. Adv. Theor. Math. Phys. 3, 1–81 (1999). arXiv:hep-th/9810201
van Nieuwenhuizen, P.: Free Graded Differential Superalgebras, In: Istanbul 1982, Proceedings, Group Theoretical Methods In Physics, pp. 228–247. 182644
Pasti, P., Sorokin, D., Tonin, M.: Branes in Super-AdS Backgrounds and Superconformal Theories, Talk at Supersymmetry and Quantum Symmetries, JINR (1999). arXiv:hep-th/9912076
Philip, S.: Plane-wave limits and homogeneous M-theory backgrounds (2005). https://www.era.lib.ed.ac.uk/bitstream/handle/1842/15645/Philip2005.Pdf?sequence=1
Quillen, D.: Rational homotopy theory. Ann. Math. (2) 90, 205–295 (1969)
Ravenel, D.: Complex cobordism and stable homotopy groups of spheres, AMS (2003). http://web.math.rochester.edu/people/faculty/doug/mu.html
Reid, M.: Young person’s guide to canonical singularities, In: Bloch, S. (ed.), Algebraic geometry – Bowdoin 1985, Part 1, Proc. Sympos. Pure Math. 46 Part 1, American Mathematical Society, Providence, RI, pp. 345–414 (1987)
Rees, E.: Notes on Geometry. Springer, Berlin (2005)
Sati, H.: M-theory and characteristic classes. J. High Energy Phys. 0508, 020 (2005). arXiv:hep-th/0501245
Sati, H.: Flux quantization and the M-theoretic characters. Nucl. Phys. B727, 461–470 (2005). arXiv:hep-th/0507106
Sati, H.: Duality symmetry and the form fields of M-theory. J. High Energy Phys. 0606, 062 (2006). arXiv:hep-th/0509046
Sati, H.: A higher twist in string theory. J. Geom. Phys. 59(3), 369–373 (2009). arXiv:hep-th/0701232
Sati, H.: Geometric and topological structures related to M-branes, Superstrings, geometry, topology, and \(C^{*}\)-algebras, 181-236, Proc. Sympos. Pure Math., 81, Amer. Math. Soc., Providence, RI, (2010). arXiv:1001.5020 [math.DG]
Sati, H.: Topological aspects of the NS5-brane. arXiv:1109.4834 [hep-th]
Sati, H.: Framed M-branes, corners, and topological invariants. J. Math. Phys. 59, 062304 (2018). arXiv:1310.1060 [hepth]
Sati, H., Schreiber, U.: Survey of mathematical foundations of QFT and perturbative string theory, Introduction to Mathematical Foundations of Quantum Field Theory and Perturbative String Theory, Amer. Math. Soc., Providence, RI, (2011). arXiv:1109.0955 [math-ph]
Sati, H., Schreiber, U.: Higher T-duality of M-branes via local supersymmetry. Phys. Lett. B 781, 694–698 (2018). arXiv:1805.00233 [hep-th]
Schmidt, M.G., Schubert, C.: The Worldline Path Integral Approach to Feynman Graphs. arXiv:hep-ph/9412358
Schreiber, U.: Differential cohomology in a cohesive \(\infty \)-topos. https://ncatlab.org/schreiber/files/dcct170811.pdf
Schreiber, U.: Higher Cartan Geometry, lecture notes, Prague (2015). https://ncatlab.org/schreiber/show/Higher+Cartan+Geometry
Schreiber, U.: Fundamental super \(p\)-Branes, lectures at: Sati, H. (org.), Flavors of Cohomology, Pittsburgh (2015). https://ncatlab.org/nlab/show/geometry+of+physics+--+fundamental+super+p-branes
Schreiber, U.: Introduction to Topology, lecture notes, Bonn (2017). https://ncatlab.org/nlab/show/Introduction+to+Topology
Schreiber, U.: Introduction to Homotopy Theory, lecture notes, Bonn (2017). https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory
Schreiber, U.: Introduction to Stable Homotopy Theory, lecture notes, Bonn (2017). https://ncatlab.org/nlab/show/Introduction+to+Stable+homotopy+theory+--+1
Schreiber, U.: Introduction to Stable Homotopy Theory— Examples and Application, lecture notes, Bonn (2017). https://ncatlab.org/nlab/show/Introduction+to+Cobordism+and+Complex+Oriented+Cohomology
Schreiber, U.: Perturbative Quantum Field Theory, lecture notes, Hamburg (2018). https://ncatlab.org/nlab/show/geometry+of+physics+--+perturbative+quantum+field+theory
Schubert, C.: An introduction to the worldline technique for quantum field theory calculations. Acta Phys. Pol. B27, 3965–4001 (1996). arXiv:hep-th/9610108
Scull, L.: Rational \(S^1\)-equivariant homotopy theory. Trans. Am. Math. Soc. 354, 1–45 (2001). (pdf)
Sen, A.: A note on enhanced gauge symmetries in M- and string theory. J. High Energy Phys. 9709, 001 (1997). arXiv:hep-th/9707123
Serrano, J.: Finite subgroups of \(SL(2,{\mathbb{C}})\) and \(SL(3,{\mathbb{C}})\), Warwick (2014). https://homepages.warwick.ac.uk/~masda/McKay/CarrascoProject.pdf
Shulman, M.: Homotopy type theory: the logic of space, In: Catren, G., Anel, M. New Spaces for Mathematics and Physics. arXiv:1703.03007
Slodowy, P.: Simple Singularities and Simple Algebraic Groups. Lecture Notes in Mathematics 815. Springer, Berlin (1980)
Sorokin, D.: Superbranes and superembeddings. Phys. Rep. 329, 1–101 (2000). arXiv:hep-th/9906142
Sorokin, D.: Introduction to the superembedding description of superbranes. AIP Conf. Proc. 589, 98 (2001). arXiv:hep-th/0105102
Spanier, E.: Borsuk’s cohomotopy groups. Ann. Math. 50, 203–245 (1949). jstor:1969362
Strominger, A.: Open P-branes. Phys. Lett. B 383, 44–47 (1996). arXiv:hep-th/9512059
Sullivan, D.: Infinitesimal computations in topology. Publ. Math. de I.H.É.S. 47, 269–331 (1977)
Suslov, I.M.: Divergent perturbation series. J. Exp. Theor. Phys. 100, 1188 (2005). arXiv:hep-ph/0510142
Townsend, P.: The eleven-dimensional supermembrane revisited. Phys. Lett. B 350, 184–187 (1995). arXiv:hep-th/9501068
Waner, S.: Equivariant homotopy theory and Milnor’s theorem. Trans. Am. Math. Soc. 258, 351–368 (1980). jstor:1998061
Wang, M.Y.: Parallel spinors and parallel forms. Ann. Glob. Anal. Geom. 7(1), 59–68 (1989)
Wellen, F.: Formalizing Cartan Geometry in Modal Homotopy Type Theory, PhD Thesis, KIT (2017). ncatlab.org/schreiber/show/thesis+Wellen
Witten, E.: String theory dynamics in various dimensions. Nucl. Phys. B443, 85–126 (1995). arXiv:hep-th/9503124
Witten, E.: Some Comments On String Dynamics, In: Bars, I. et. al, (eds.) Proceedings of String95. arXiv:hep-th/9507121
Witten, E.: Five-branes and M-theory on an orbifold. Nucl. Phys. B 463, 383–397 (1996). arXiv:hep-th/9512219
Witten, E.: D-branes and K-theory. J. High Energy Phys. 12, 019 (1998). arXiv:hep-th/9810188
Witten, E.: Singularities in string theory, Proceedings of the ICM, Beijing 1, 495–504 (2002). arXiv:hep-th/0212349
Witten, E.: Viewpoints on String Theory, NOVA interview (2003). www.pbs.org/wgbh/nova/elegant/view-witten.html
Witten, E.: What every physicist should know about string theory, talk at Strings2015 strings2015.icts.res.in/talkDocuments/26-06-2015-Edward-Witten.pdf
Acknowledgements
We thank Vincent Braunack-Mayer, David Corfield, Mike Duff, David Roberts, and Christian Saemann for useful comments. We thank the anonymous referee for careful reading and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Schweigert
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Urs Schreiber: on leave from Czech Acad. of Science, Prague.
Mathematics Background and Conventions
Mathematics Background and Conventions
For ease of reference, here we collect some standard background material that we use in the main text: on Spacetime and Spin in Sect. A.1 and on Homotopy and Cohomology in Sect. A.2.
1.1 Spacetime and spin
For reference and to fix some essential conventions, we briefly recall some details on real Spin representations in Lorentzian signature.
Definition A.1
(Spin geometry of Minkowski spacetime). For \(p \in \mathbb {N}\) we write \(\mathbb {R}^{p,1}\) for the corresponding Minkowski spacetime. The underlying real vector space is \(\mathbb {R}^{p+1}\).
- (i):
-
With its canonical coordinate functions labeled as \((x^0, x^1, \ldots , x^p)\), the inner product (Minkowski metric) is taken with the mostly plus signature: for two vectors u and v in \(\mathbb R^{p,1}\), we have
$$\begin{aligned} \eta (u,v) = -u^0 v^0 + u^1 v^1 + \cdots + u^p v^p \,. \end{aligned}$$(68) - (ii):
-
We write
$$\begin{aligned} \mathrm{C}\ell (p,1) \;:=\; \mathbb R\langle \varvec{\Gamma }_0, \varvec{\Gamma }_1, \ldots , \varvec{\Gamma }_p \rangle / \left( \varvec{\Gamma }_a \cdot \varvec{\Gamma }_b + \varvec{\Gamma }_b \cdot \varvec{\Gamma }_a = + 2 \eta _{a,b}\right) \end{aligned}$$(69)for the Clifford algebra of \(\mathbb R^{p,1}\). This is the quotient of the free real associative algebra on \(p+1\) generators \(\varvec{\Gamma }_a\) by the Clifford relation, which says that their anticommutator is twice the corresponding entry in the Minkowski metric. We write
$$\begin{aligned} \varvec{\Gamma }_{a_1 \cdots a_q} \;:=\; \tfrac{1}{q!} \underset{\sigma \in \Sigma _q}{\sum } (-1)^{{\vert \sigma \vert }} \varvec{\Gamma }_{a_{\sigma (1)}} \cdot \varvec{\Gamma }_{a_{\sigma (2)}} \cdots \cdot \varvec{\Gamma }_{a_{\sigma (q)}} \end{aligned}$$(70)for the skew-symmetrized products of the Clifford generators.
- (iii):
-
Recall the various groups acting on Minkowski spacetime:
-
the Lorentz group\(\mathrm{O}(p,1) \hookrightarrow \mathrm {GL}(p+1)\) is the subgroup of linear transformations that preserve the Minkowski metric (68);
-
the orthochronous Lorentz group\(\mathrm{O}^+(p,1) \hookrightarrow \mathrm{O}(p,1)\) is the subgroup of transformations that preserve time-orientation;
-
the Pin group\(\mathrm{Pin}(p,1) \rightarrow \mathrm{O}(p,1)\) is the double cover of the Lorentz group given by the standard Clifford algebraic construction: the group \(\mathrm{Pin}(p,1)\) is the subgroup of invertible elements of the Clifford algebra generated by unit vectors in \(\mathbb R^{p,1}\):
$$\begin{aligned} \mathrm{Pin}(p,1) : = \langle u \in \mathbb R^{p,1} \, : \, \eta (u,u) = \pm 1 \rangle \subseteq \mathrm{C}\ell (p,1) . \end{aligned}$$A unit vector \(u \in \mathrm{Pin}(p,1)\) maps to the reflection in \(\mathrm{O}(p,1)\) through the hyperplane orthogonal to u, and this map on generators extends to a homomorphism \(\mathrm{Pin}(p,1) \rightarrow \mathrm{O}(p,1)\). It is well known that this homomorphism is a double cover.
-
the orthochronous Pin group\(\mathrm{Pin}^+(p,1) \rightarrow \mathrm{O}^+(p,1)\) is subgroup of \(\mathrm{Pin}(p,1)\) that double covers the orthochronous Lorentz group \(\mathrm{O}^+(p,1)\).
-
the Spin group\(\mathrm{Spin}(p,1) \rightarrow \mathrm{SO}^+(p,1)\) is the subgroup of \(\mathrm{Pin}(p,1)\) that double covers the connected Lorentz group \(\mathrm{SO}^+(p,1)\). In terms of the Clifford algebra, it is the subgroup of invertible elements generated by products of pairs of unit vectors with the same sign:
$$\begin{aligned} \mathrm{Spin}(p,1) = \langle uv \in \mathrm{C}\ell (p,1) : u,v \in \mathbb R^{p,1} \text{ and } \eta (u,u) = \eta (v,v) = \pm 1 \rangle . \end{aligned}$$The Lie group \(\mathrm{Spin}(p,1)\) is connected and simply-connected.
-
The Lie algebra of the Spin group is the Lie subalgebra of the Clifford algebra on commutators of vectors:
$$\begin{aligned} \mathrm{Lie}(\mathrm{Spin}(p,1)) \simeq \{ [u,v] \in \mathrm{C}\ell (p,1) : u,v \in \mathbb R^{p,1} \} . \end{aligned}$$Note that this subspace is actually a Lie subalgebra with respect to the commutator in \(\mathrm{C}\ell (p,1)\). The double cover map \(\mathrm{Spin}(p,1) \rightarrow \mathrm{SO}^+(p,1)\) induces an isomorphism of Lie algebras
$$\begin{aligned} \mathrm{Lie}(\mathrm{Spin}(p,1) \simeq \mathfrak {so}(p,1) \end{aligned}$$with the Lorentz Lie algebra \(\mathfrak {so}(p,1)\) of the connected Lorentz group \(\mathrm{SO}^+(p,1)\).
Note that because the Spin group \(\mathrm{Spin}(p,1)\) is connected and simply-connected, we can describe a representation in two ways:
- 1.:
-
We can give the action of the generators \(uv \in \mathrm{Spin}(p,1)\) on a vector space, where u and v are unit vectors of the same sign.
- 2.:
-
We can give the action of the Lie algebra \(\mathfrak {so}(p,1)\) on a vector space, and exponentiate to get the action of the Lie group \(\mathrm{Spin}(p,1)\). In particular, it suffices to give the action of a basis of the Lie algebra \(\{ [u,v] \in \mathrm{C}\ell (p,1) : u,v \in \mathbb R^{p,1} \}\). A natural choice is the basis given by skew-symmetrized products of two gamma matrices, \(\{ \Gamma _{ab} \}\).
Remark A.2
(Technology for real Spin representations). There are two alternative ways of constructing and handling the real Spin representations that appear in the super-Minkowski spacetimes in Definition 3.36:
-
One may carve out real Spin representations from complex Dirac or Weyl representations by imposing a reality condition, called the Majorana condition. This is the standard method used in the physics literature. A textbook reference for standard conventions is [CDF91, Sec. II.7], while a conceptual account is in [FF]. We recall this as Proposition A.3 below; this serves for comparing the results in Sects. 4, 5, and 6 to the bulk of the string theory literature.
-
Alternatively, one may use the real normed division algebras and matrices over them. The most famous example of this is identifying 4-dimensional spacetime, \(\mathbb R^{3,1}\), with the \(2 \times 2\) complex hermitian matrices, and generating the Weyl representations of \(\mathrm{Spin}(3,1)\) on \(\mathbb {C}^2\) from the action of these matrices. Yet this sort of construction continues to work for normed division algebras other than \(\mathbb {C}\), and for spacetimes other than dimension 4. We recall this approach in Sect. A.1 below; this serves to streamline the proofs of the theorems in Sects. 4, 5, and 6.
1.1.1 Real Pin-representations via Majorana condition
Proposition A.3
(Real spinors via Majorana conditions on Dirac representations). Let
and let \(N = 2^{\nu }\).
- (i):
-
Dirac representations (as in [CDF91, Sec. II.7.1]): There exist complex matrices
$$\begin{aligned} \Gamma _a \;\in \; \mathrm{End}_{\mathbb {C}}\left( \mathbb {C}^N \right) , a \in \{0,1, \ldots , p\} \end{aligned}$$with the following properties:
$$\begin{aligned} \begin{array}{cl} \Gamma _a \Gamma _b + \Gamma _b \Gamma _a = - 2 \eta _{a b}\;, &{} \\ \left( \Gamma _0\right) ^2 = +1\;,\qquad \left( \Gamma _a\right) ^2 = -1 \,, &{} \\ (\Gamma _0)^{\dagger } = \Gamma _0\;,\qquad (\Gamma _a)^{\dagger } = - \Gamma _a\;, &{} \qquad \text{ for }\ a,b \in \{1,\ldots , p\}. \end{array} \end{aligned}$$(71) - (ii):
-
Charge conjugation matrices (as in [CDF91, Sec. II.7.2]): Moreover, there exist charge conjugation matrices
$$\begin{aligned} C_{(\pm )} \in \mathrm {End}_{\mathbb {C}}( \mathbb {C}^{N} ) \end{aligned}$$with real entries \((C_{(\pm )})^{*} = C_{(\pm )}\) and related to the above \(\Gamma \)-matrices by \(C_{(\pm )} \Gamma = \pm \Gamma _a^t C_{(\pm )}\) according to the following table:
$$\begin{aligned} \begin{array}{|c|c|c|} \hline p + 1 &{} C_{(+)} &{} C_{(-)}\\ \hline \hline 3+1 &{} *&{} *\\ \hline 4+1 &{} *&{}\\ \hline 5+1 &{} *&{} *\\ \hline 6+1 &{} &{} *\\ \hline 7+1 &{} *&{} *\\ \hline 8+1 &{} *&{}\\ \hline 9+1 &{} *&{} *\\ \hline 10+1 &{} &{} *\\ \hline \end{array} \end{aligned}$$(72) - (iii):
-
Majorana condition (as in [CDF91, Sec. II.7.3]): Given a Dirac spinor \(\psi \in \mathbb {C}^{N}\) we say that its Dirac conjugate is
$$\begin{aligned} \overline{\psi } \;:=\; \psi ^{\dagger } \Gamma _0 \,. \end{aligned}$$(73)This \(\psi \) is called a Majorana spinor if its Dirac conjugate equals its Majorana conjugate, which means
 (74)
(74) - (iv):
-
Majorana Spin representations (see [FF]): The subspace of Majorana spinors inside \(\mathbb {C}^{N}\)
$$\begin{aligned} \mathbf {N} \subset \mathbb {C}^{N}. \end{aligned}$$is preserved by multiplication by the \(\Gamma _{a b}\). This set is a basis for \(\mathfrak {so}(p,1)\) and this defines a real representation of \(\mathrm{Spin}(p,1)\) on \(\mathbf{N}\) with dimension \(N = 2^{\nu }\). The Dirac conjugation (73) induces on \(\mathbf{N}\) the following quadratic and \(\mathrm {Spin}(p,1)\)-equivariant spinor-to-vector pairing
 (75)
(75) - (v):
-
Majorana Pin representations: For charge conjugation matrix \(C_{(+)}\), the action of a single \(\Gamma _a\) preserves the Majorana condition. But for \(C_{(-)}\) it does not. For \(C_{(-)}\) instead the product \(i \Gamma _a\) preserves the Majorana condition. We will write
$$\begin{aligned} \varvec{\Gamma }_a := i {\Gamma }_a \,. \end{aligned}$$Instead of the relations (71), the relations satisfied by these boldface gamma matrices are the following:
$$\begin{aligned} \begin{array}{cl} \varvec{\Gamma }_a \varvec{\Gamma }_b + \varvec{\Gamma }_b \varvec{\Gamma }_a = + 2\eta _{a b}\;, &{} \\ \left( \varvec{\Gamma }_0\right) ^2 = -1\;,\qquad \left( \varvec{\Gamma }_a\right) ^2 = +1\;, &{} \\ (\varvec{\Gamma }_0)^{\dagger } = - \varvec{\Gamma }_0\;,\qquad (\varvec{\Gamma }_a)^{\dagger } = + \varvec{\Gamma }_a\;, &{} \qquad \text{ for }\ a \in \{1,\ldots , p\}, \end{array} \end{aligned}$$(76)Since now, for \(C_{(-)}\), the subspace of Majorana spinors inside \(\mathbb {C}^{N}\) is preserved by the action of each \(\varvec{\Gamma }_a\), equipped with this action it is a real representation of the Pin group (Remark A.2) \(\mathbf {N} \subset \mathbb {C}^{N}\) of real dimension \(N = 2^{\nu }\).
Example A.4
(Real Spin representations). The following are the irreducible real representations (up to isomorphism) of \(\mathrm {Spin}(p,1)\) (Definition A.1) for values of p of relevance in the main text, obtainable via Proposition A.3:
Spacetime dimension \(p + 1\) | Supersymmetry \(\mathbf {N}\) |
|---|---|
\(10 + 1\) | \(\mathbf {32}\) |
\(9 +1\) | \(\mathbf {16}\), \(\overline{\mathbf {16}}\) |
\(6 + 1\) | \(\mathbf {16}\) |
\(5 + 1\) | \(\mathbf {8}\), \(\overline{\mathbf {8}}\) |
\(4 + 1\) | \(\mathbf {8}\) |
\(3+1\) | \(\mathbf {4}\) |
\(2+1\) | \(\mathbf {2}\) |
\(1 + 1\) | \(\mathbf {1}\), \(\overline{\mathbf {1}}\) |
We are particularly interested in the \(\mathbf {32}\) of \(\mathrm {Spin}(10,1)\). Notice that by (72) the charge conjugation matrix in \(D = 10+1 \) is \(C_{(-)}\) and hence the gamma matrices representing the \(\mathrm {Pin}(10,1)\)-action on \(\mathbf {32}\) are those from (76).
Remark A.5
(Notation for Irrep decomposition – Number of supersymmetries). Given irreducible real spinor representations \(\mathbf {N}\) or \(\overline{\mathbf {N}}\) as in Example A.4, a general real spinor representation \(\Delta \) is a direct sum of these. The multiplicities of the direct summands is traditionally denoted by \(\mathcal {N}\) or \(\mathcal {N}_{\pm } \in \mathbb {N}\):
Hence if the irreducible representations are understood, any other representation may be denoted simply by
When these real spinor representations serve as constituents of super Minkowski spacetimes (Definition 3.36) one calls the natural numbers \(\mathcal {N}\) or \(\mathcal {N}_{\pm }\) the number of supersymmetries.
1.1.2 Spinor representations via normed division algebras
The observation that real \(\mathrm {Spin}(p,1)\)-representations for \(p+1 \in \{3,4,5,6,7,10,11\}\) may be related to the real division algebras is due to [KuTo82]. A comprehensive account is given in [BH10, BH11]. Here we briefly recall the facts that we need.
Definition A.6
(Cayley–Dickson construction). Let A be a real star-algebra (unitual, but not necessarily commutative nor associative), with star involution denoted by \(\overline{(-)}\). Then its Cayley–Dickson double\(\mathrm {CD}(A)\) is the real star algebra obtained by adjoining a new generator \(\ell \) subject to the following relations:
for all \(a, b \in A\). This implies that the underlying real vector space is
Example A.7
(The four real normed division algebras). The first iterations of the Cayley–Dickson construction (Definition A.6) yield the real algebras of
- 1.:
-
real numbers \(\mathbb {R}\),
- 2.:
-
complex numbers \(\mathbb {C} \simeq \mathrm {CD}(\mathbb {R})\),
- 3.:
-
quaternions \(\mathbb {H} \simeq \mathrm {CD}(\mathbb {C})\),
- 4.:
-
octonions \(\mathbb {O} \simeq \mathrm {CD}(\mathbb {H})\).
These four algebras also happen to be precisely the finite-dimensional ‘normed division algebras’ over the real numbers. Recall that a normed division algebra \({\mathbb {K}}\) is a real algebra, not necessarily associative, with unit 1 and equipped with a norm \(|\cdot |\) such that:
We say that an algebra equipped with such a norm is normed. Note that being normed immediately implies that \({\mathbb {K}}\) has no zero divisors, so \({\mathbb {K}}\) is indeed a division algebra.
Remarkably, there are only four normed division algebras: \(\mathbb R\), \(\mathbb {C}\), \({\mathbb {H}}\) and \({\mathbb {O}}\), constructed above. In the first step of this construction, going from \(\mathbb {R}\) to \(\mathbb {C}\), the adjoined generator \(\ell \) is identified with the imaginary unit \(i \in \mathbb {C}\). In the second step the adjoined generator is usually denoted j, leading to the imaginary quaternions subject to the relations
and their cyclic permutations. When working with the octonions, we will exclusively use the Cayley–Dickson presentation, and hence in the main text \(\ell \) always denotes a unit octonion orthogonal to i, j and \(k := i j\). Notice simple but important relations implied by (77), such as \( \ell ^{-1} = - \ell \), which lead to manipulations such as
Proposition A.8
(Basic properties of the quaternions). We collect some well-known facts about quaternions (Example A.7):
- (i):
-
The quaternions \(\mathbb {H}\) are isomorphic to \(\mathbb {R}^4\) as a normed vector space:
$$\begin{aligned} \mathbb {H} \simeq \mathbb {R}^4\;. \end{aligned}$$(79) - (ii):
-
A quaternion \(q \in \mathbb {H}\) of unit norm \(\vert q\vert = 1\) is also called a unit quaternion, for short. As a submanifold of \(\mathbb {H}\), the space of unit quaternions is the 3-sphere
$$\begin{aligned} S(\mathbb {H}) \simeq S^3 \,. \end{aligned}$$Quaternion multiplication turns \(S({\mathbb {H}})\) into a Lie group. This group is isomorphic to \(\mathrm {SU}(2)\):
$$\begin{aligned} S(\mathbb {H}) \simeq \mathrm {SU}(2) \,. \end{aligned}$$(80) - (iii):
-
Thanks to quaternion multiplication, the group \(\mathrm{SU}(2)\) acts on \(\mathbb {H}\) in two ways (Definition 3.7):
 (81)
(81)These actions commute with each other because \({\mathbb {H}}\) is associative, and they preserve the norm because \({\mathbb {H}}\) is normed:
$$\begin{aligned} \vert q v\vert = \underset{=1}{\underbrace{{\vert q\vert }}} \, \vert v\vert ={\vert v\vert } \,, \end{aligned}$$with a similar calculation for the right action. Finally, in either case \(\mathrm{SU}(2)\) acts on \({\mathbb {H}}\) by orientation-preserving transformations, because \(\mathrm{SU}(2)\) is connected. In summary, the two actions \(\rho _{L,R}\) of \(\mathrm {SU}(2)\) factor through the special orthogonal group in 4 dimensions:
 (82)
(82) - (iv):
-
Because the actions \(\rho _L\) and \(\rho _R\) commute with each other, they define an action of \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) on \({\mathbb {H}}\). Restricting this to the diagonal \(\mathrm{SU}(2)\) subgroup, we get an action of \(\mathrm{SU}(2)\) on \({\mathbb {H}}\):
$$\begin{aligned} \mathrm{SU}(2) \times {\mathbb {H}}&\longrightarrow {\mathbb {H}}\;. \\ (q,v)&\mapsto qv\bar{q} \end{aligned}$$This action is trivial on the real quaternions, and preserves the 3-dimensional subspace of imaginary quaternions. In fact, \({\mathbb {H}}\) decomposes into the irreducible representations:
$$\begin{aligned} {\mathbb {H}}\simeq \mathbb R\oplus \mathrm {Im}({\mathbb {H}}) . \end{aligned}$$The action of \(\mathrm{SU}(2)\) on the summand \(\mathrm {Im}({\mathbb {H}})\) preserves the norm, and this induces the famous homomorphism
$$\begin{aligned} \mathrm{SU}(2) \rightarrow \mathrm{SO}(3) , \end{aligned}$$(83)a double cover of \(\mathrm{SO}(3)\).
The finite subgroups of \(\mathrm{SU}(2)\) are of particular interest in the main text:
Remark A.9
(The finite subgroups of \(\mathrm {SU}(2)\) [Klein1884]). The finite subgroups of \(\mathrm {SU}(2)\) are given, up to conjugacy, by the following classification (where \(n \in \mathbb {N}\)):
Label | Finite subgroup of \(\mathrm {SU}(2)\) | Name of group |
|---|---|---|
\(\mathbb {A}_{n}\) | \(\mathbb {Z}_{n+1}\) | Cyclic |
\(\mathbb {D}_{n+4}\) | \(2\mathrm {D}_{n+2}\) | Binary dihedral |
\(\mathbb {E}_{6}\) | \(2\mathrm {T}\) | Binary tetrahedral |
\(\mathbb {E}_{7}\) | \(2\mathrm {O}\) | Binary octahedral |
\(\mathbb {E}_{8}\) | \(2\mathrm {I}\) | Binary icosahedral |
The full proof for the case of finite subgroups of \(\mathrm {SL}(2,\mathbb {C})\) is given in [MBD1916], recalled in detail in [Ser14, Sec. 2]. Full proof for the case of \(\mathrm {SO}(3)\) is also spelled out in [Ree05, Theorem 11]; from this the proof for the case of \(\mathrm {SU}(2)\) is spelled out in [Kee03, Theorem 4].
Definition A.10
(Hopf fibration). Let \(\mathbb {K}\) be one of the four normed division algebras (Example A.7). Then the corresponding Hopf fibration is the map between unit spheres given by

where S(V) denotes the unit sphere inside the normed vector space V. The image lies in \(S(\mathbb R\oplus {\mathbb {K}})\) because the normed division algebra is normed.
Hence we have
The key statement for us is the following:
Proposition A.11
(Real Spin representations via real normed division algebras (see [BH10, BH11])). Let \({\mathbb {K}}\in \{\mathbb {R}, \mathbb {C}, \mathbb {H}, \mathbb {O}\}\) be one of the normed division algebras (Example A.7). Write \(\mathfrak {h}_2({\mathbb {K}})\) for the real vector space of \(2 \times 2\) hermitian matrices with coefficients in \({\mathbb {K}}\):
Let k denote the dimension of \({\mathbb {K}}\). Then:
Normed algebra | Hopf fibration |
|---|---|
\(\mathbb {R}\) | \(S^1 \quad \overset{\cdot 2}{\longrightarrow } \quad S^1\) |
\(\mathbb {C}\) | \(S^3 \quad \longrightarrow \quad S^2\) |
\(\mathbb {H}\) | \(S^7 \quad \longrightarrow \quad S^4\) |
\(\mathbb {O}\) | \(S^{15} \quad \longrightarrow \quad S^8\) |
-
1.
There is an isomorphism of inner product spaces (“forming Pauli matrices over \(\mathbb {K}\)”)
$$\begin{aligned} \left( \mathfrak {h}_2({\mathbb {K}}), -\mathrm {det} \right) {\mathop {\longrightarrow }\limits ^{\simeq }} (\mathbb {R}^{k+1,1}, \eta ) \end{aligned}$$identifying \(\mathbb {R}^{k+1,1}\) equipped with its Minkowski inner product
$$\begin{aligned} \eta (A,B) := -A^0 B^0 + A^1 B^1 + \cdots + A^{k+1} B^{k+1}, \text{ for } A, B \in \mathbb R^{k+1,1} \end{aligned}$$with the space of \(2 \times 2\) hermitian matrices equipped with the negative of the determinant operation.
-
2.
Let \(\mathbf{N}\) and \(\overline{\mathbf{N}}\) both denote the vector space \({\mathbb {K}}^2\). Then \(\mathbf{N} \oplus \overline{\mathbf{N}}\) is a module of the Clifford algebra \(\mathrm{C}\ell (k+1,1)\), with the action of a vector in \(A \in \mathbb R^{k+1,1}\) given by
$$\begin{aligned} \Gamma (A) (\psi , \phi ) = (\tilde{A}_L \phi , A_L \psi ) \end{aligned}$$for any element \((\psi , \phi ) \in \mathbf{N} \oplus \overline{\mathbf{N}}\), where we are using the identification of vectors in \(\mathbb R^{k+1,1}\) with \(2 \times 2\) hermitian matrices. Here \(\widetilde{(-)}\) is the operation \(\widetilde{A} = A - \mathrm {tr}(A) 1\), and \((-)_L\) denotes the linear map given by left multiplication by a matrix.
-
3.
Realizing the Spin group \(\mathrm{Spin}(k+1,1)\) inside the Clifford algebra \(\mathrm{C}\ell (k+1,1)\) by the standard construction, this induces irreducible representations \(\rho \) and \(\overline{\rho }\) of \(\mathrm{Spin}(k+1,1)\) on \(\mathbf{N}\) and \(\overline{\mathbf{N}}\), respectively. Explicitly, recall that \(\mathrm{Spin}(k+1,1)\) is the subgroup of the Clifford algebra generated by products of pairs of unit vectors of the same sign:
$$\begin{aligned} \mathrm{Spin}(k+1, 1) = \langle AB \in \mathrm{C}\ell (k+1,1) \, : \, A, B \in \mathbb R^{k+1,1} \text{ and } \eta (A,A) = \eta (B,B) = \pm 1 \rangle . \end{aligned}$$Then restricting the Clifford action to these elements, a generator AB of \(\mathrm{Spin}(k+1,1)\) acts as
$$\begin{aligned} \rho (AB) = \tilde{A}_L B_L \text{ on } \mathbf{N} \end{aligned}$$and as
$$\begin{aligned} \overline{\rho }(AB) = A_L \tilde{B}_L \text{ on } \overline{\mathbf{N}}, \end{aligned}$$where again \(\widetilde{(-)}\) is the operation \(\widetilde{A} = A - \mathrm {tr}(A) 1\), and \((-)_L\) denotes the linear map given by left multiplication by a matrix.
-
4.
Moving up by one dimension, there is an isomorphism of inner product spaces
$$\begin{aligned} \left\{ \left( \begin{array}{cc} x^0 &{} \widetilde{A}\\ A &{} - x^0 \end{array}\right) \;:\; a \in \mathbb {R} \,, A \in \mathfrak {h}_2( \mathbb {K} ) \right\} \;\simeq \; \mathbb {R}^{k+2,1} \end{aligned}$$between the subspace on the right of \(4 \times 4\) matrices over \({\mathbb {K}}\), equipped with the inner product given by \(-\mathrm {det}(A) + a^2\), and Minkowski spacetime \(\mathbb R^{k+2,1}\).
-
5.
Let \(\mathscr {N}\) denote the vector space \({\mathbb {K}}^4\). Then \(\mathscr {N}\) is a module of the Clifford algebra \(\mathrm{C}\ell (k+2,1)\) with the action of a vector \(\mathcal {A} \in \mathbb R^{k+2,1}\) given by:
$$\begin{aligned} \Gamma (\mathcal {A}) \Psi = \mathcal {A}_L \Psi \end{aligned}$$for any element \(\Psi \in \mathscr {N}\). Here we are using the identification of vectors in \(\mathbb R^{k+2,1}\) with a subspace of \(4\times 4\) matrices over \({\mathbb {K}}\), and \((-)_L\) denotes the linear operator given by left multiplication by a matrix.
-
6.
Realizing the Spin group \(\mathrm{Spin}(k+2,1)\) inside the Clifford algebra \(\mathrm{C}\ell (k+2,1)\) by the standard construction, this induces an irreducible representation \(\rho \) of \(\mathrm{Spin}(k+2,1)\) on \(\mathscr {N}\). Explicitly, recall that \(\mathrm{Spin}(k+2,1)\) is the subgroup of the Clifford algebra generated by products of pairs of unit vectors of the same sign:
$$\begin{aligned} \mathrm{Spin}(k+2, 1) = \langle \mathcal {A}\mathcal {B}\in \mathrm{C}\ell (k+2,1) \, : \, \mathcal {A}, \mathcal {B}\in \mathbb R^{k+2,1} \text{ and } \eta (\mathcal {A},\mathcal {A}) = \eta (\mathcal {B},\mathcal {B}) = \pm 1 \rangle . \end{aligned}$$Then restricting the Clifford action to these elements, a generator \(\mathcal {A}\mathcal {B}\) of \(\mathrm{Spin}(k+2,1)\) acts as
$$\begin{aligned} \rho (\mathcal {A}\mathcal {B}) = \mathcal {A}_L \mathcal {B}_L \text{ on } \mathscr {N} \end{aligned}$$where again \((-)_L\) denotes the linear map given by left multiplication by a matrix.
-
7.
The representations \(\mathbf{N}\), \(\overline{\mathbf{N}}\) and \(\mathscr {N}\) constructed above are the irreducible real spinor representations in the following table (and as in Example A.4):
Dimension \(D = p + 1\)
Real irreps of \(\mathrm {Spin}(p,1)\)
Clifford modules via real normed division algebra
\(\{\widetilde{\sigma }\sigma \}\)
\(\left\{ \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array}\right) \;, \; \left\{ \left( \begin{array}{cc} 0 &{} \tilde{\sigma } \\ \sigma &{} 0 \end{array}\right) \right\} \right\} \)
\(\{\sigma \widetilde{\sigma }\}\)
\(10+1\)
\(\mathbf {32}\)
\(\mathbb {O}^4\)
\(9+1\)
\(\mathbf {16}\), \(\overline{\mathbf {16}}\)
\(\mathbb {O}^2\)
\(\mathbb {O}^2\)
\(6+1\)
\(\mathbf {16}\)
\(\mathbb {H}^4\)
\(5+1\)
\(\mathbf {8}\), \(\overline{\mathbf {8}}\)
\(\mathbb {H}^2\)
\(\mathbb {H}^2\)
\(4+1\)
\(\mathbf {8}\)
\(\mathbb {C}^4\)
\(3+1\)
\(\mathbf {4}\)
\(\mathbb {C}^2\)
\(\simeq \)
\(\mathbb {R}^4\)
\(\simeq \)
\(\mathbb {C}^2\)
\(2+1\)
\(\mathbf {2}\)
\(\mathbb {R}^2\)
\(\simeq \)
\(\mathbb {R}^2\)
Here the symbol “\(\simeq \)” in the last two lines denotes isomorphism of real representations.
Example A.12
(The octonionic presentation of \(\mathbf {32}\)). We can identify the 32-dimensional vector space \(\mathbf{32}\) with the space \({\mathbb {O}}^4\):
Under this identification, the Clifford algebra \(\mathrm {Cl}(10,1)\) (see (69)) acts on \(\mathbf{32}\) by left multiplication by the following \(4 \times 4\) matrices with entries in the octonions, written as \(2 \times 2\) matrices with \(2 \times 2\) blocks:
Here, besides the imaginary octonions \(e_1, \ldots , e_7\), we have used the \(2 \times 2\) real matrices:
Defining the tensor product of matrices A and B to be the matrix
we can rewrite the octonionic gamma matrices (85) as follows:
1.2 Homotopy and cohomology
For reference, here we collect some basics of abstract homotopy theory and of the associated generalized cohomology theories.
1.2.1 Homotopy theory
We briefly recall some basics of homotopy theory, as well as some basic examples of relevance in the main text. For a self-contained introductory account of abstract homotopy theory see [Sch17b]. For minimal background on language of categories required, see [Sch17a, around Remark 3.3], and for a comprehensive reference see [Bor94]. For going deep and far into homotopy theory, see [Lu09-]. For exposition of the foundational role of homotopy theory see [Sh17].
Definition A.13
(Category with weak equivalences (e.g. [Sch17b, Def. 2.1])). A category with weak equivalences is a category \(\mathcal {C}\) equipped with a choice of sub-class \(W \subset \mathrm {Mor}(\mathcal {C})\) of its morphisms, called the weak equivalences, such that
-
1.
W contains all the identity morphisms;
-
2.
if \(f,g \in W\) are composable with composite \(g \circ f \), and if two elements in the set \(\{f, g, g \circ f \}\) are weak equivalences, then also the third is.
A category with weak equivalences may also be called a homotopy theory.
Definition A.14
(Homotopy categories (e.g. [Sch17b, Def. 2.30])). Given a category with weak equivalences \((\mathcal {C},W)\) (Definition A.13), then its homotopy category is the category \(\mathrm (Ho)( \mathcal {C}[W^{-1}] )\) equipped with a functor
called the localization functor, such that
-
1.
\(\gamma \) sends weak equivalences to actual isomorphisms;
-
2.
\(\left( \mathrm {Ho}\left( \mathcal {C}\left[ W^{-1}\right] \right) ), \gamma \right) \) is the universal solution with this property, in that if \(F :\mathcal {C} \rightarrow \mathcal {D} \) is any other functor, to any other category, such that it sends the weak equivalences W to actual isomorphisms, then F actually factors through \(\gamma \), up to natural isomorphism

and this factorization is unique up to unique isomorphism.
The following are basic examples of homotopy theories.
Definition A.15
(Compactly generated topological spaces). By a topological space we will always mean a compactly generated topological space (e.g. [Sch17b, Def. 3.35]). We write “\(\mathrm {Spaces}\)” for the category whose objects are compactly generated topological spaces, and whose morphism are continuous functions. For X, Y two such topological spaces, the space
of continuous functions between them is itself naturally a compactly generated topological space (e.g. [Sch17b, Def. 3.39]) satisfying the universal properties of a mapping space (e.g. [Sch17b, Def. 3.41]).
Definition A.16
(Classical homotopy theory (e.g. [Sch17b, Def. 3.11])). A continuous function \(f :X \rightarrow Y\) between topological spaces (Definition A.15) is called a weak homotopy equivalence if it induce a bijection between connected components

and, for every \(n \in \mathbb {N}\), \(n \ge 1\) and every base point \(x \in X\), it induces an isomorphism between the nth homotopy groups

The resulting homotopy category (Definition A.14)
is also called the classical homotopy category.
Example A.17
(Based path spaces). For X any topological space (Definition A.15), equipped with a base point \(x \in X\), write
for its based path space, the subspace of the space of continuous functions \(\gamma :[0,1] \longrightarrow X\) from the interval to X which take \(0 \in [0,1]\) to the base point \(\gamma (0) = x\). There is then the endpoint evaluation map

Moreover, there is the unique map to the point \(P_x X \longrightarrow *\). This is a weak homotopy equivalence (Definition A.16). Observe that a continuous function \(\widehat{f}\) into a based path space is equivalently a continuous function into X equipped with a homotopy (Definition 3.14) to the function that is constant on the base point:

It turns out that the classical homotopy category is an extremely rich structure. In order to get a handle on these categories, one may filter them in various ways such as to study homotopy types in controlled approximations. A key instance of this is the rational approximation. We recall this as Proposition A.20 below.
Definition A.18
(Rational homotopy theory ([Qu69] e.g. [Hes06])).
- (i):
-
A continuous function \(f :X \rightarrow Y\) between topological spaces (Definition A.15) is called a rational weak homotopy equivalences if it induces a bijection between connected components

and for every \(n \in \mathbb {N}\), \(n \ge 1\) and every base point \(x \in X^H\) they induce an isomorphism between the rationalized \(n\hbox {th}\) homotopy groups

- (ii):
-
The resulting homotopy category (Definition A.14)
$$\begin{aligned} \mathrm {Ho}\left( \mathrm {Spaces}_{\mathbb {R}} \right) \;:=\; \mathrm {Ho} \left( \mathrm {Spaces}\left[ \left\{ \text{ rational } \text{ weak } \text{ homotopy } \text{ equivalences } \right\} \right] \right) \end{aligned}$$is also called the rational homotopy category.
- (iii):
-
We also consider the full subcategory

on those spaces X which are
-
of finite rational type i.e. \(H^1(X,\mathbb {Q})\) and \(\pi _{k\ge 2}(X) \otimes \mathbb {Q}\) are finite-dimensional \(\mathbb {Q}\)-vector spaces for all \(k \ge 2\);
-
nilpotent i.e. the fundamental group \(\pi _1(X)\) is a nilpotent group and such that its action on the higher rational homotopy groups is nilpotent (i.e., making them nilpotent \(\pi _1(X)\)-modules).
The key point about rational homotopy theory (Definition A.18) is that it may be modeled by dg-algebraic means:
Definition A.19
(Rational DG-algebraic homotopy theory (e.g. [Hes06])).
- (i):
-
We write \(\mathrm {dgcAlg}\) for the category whose objects are differential graded-commutative \(\mathbb {R}\)-algebras and whose morphisms are dg-algebra homomorphisms. A morphism \(\phi :A_1 \rightarrow A_2\) is called a quasi-isomorphism if it induces isomorphisms on all cochain cohomology groups:
$$\begin{aligned} H^n(\phi ) :H^n(A_1) \overset{\simeq }{\longrightarrow } H^n( A_2 ) \,. \end{aligned}$$ - (ii):
-
We write the corresponding homotopy category (Definition A.14) as
$$\begin{aligned} \mathrm {Ho}\left( \mathrm {dgcAlg}^{\mathrm {op}} \right) \;:=\; \mathrm {Ho}\big ( \mathrm {dgcAlg}^{\mathrm {op}} \big [ \left\{ \text{ quasi-isomorphisms }\right\} ^{-1} \big ] \big ) \,. \end{aligned}$$ - (iii):
-
We also consider the full subcategory

on those algebras A which are
-
of finite type in that they are equivalent to a DGC-algebra that is degreewise finitely generated;
-
connected in that the unit inclusion \(\mathbb {Q} \rightarrow A\) induces an isomorphism \(\mathbb {Q} \simeq H^0(A)\).
- (iv):
-
Finally we writeFootnote 16
$$\begin{aligned} \underset{S \in \mathrm {Set}}{\int } \mathrm {Ho}\big (\mathrm {dgcAlg}^{\mathrm {op}}_{\mathrm {fin}, \mathrm {cn}} \big )^S \end{aligned}$$(89)for the category whose objects are pairs consisting of a set S and an S-indexed tuple of objects of the homotopy category of connected finite-type dgc-algebras, and whose morphism are pairs consisting of a function between these sets and a tuple of homomorphisms between the corresponding dgc-algebras.
The following is the classical statement of rational homotopy theory:
Proposition A.20
(DG-model for rational homotopy theory ([Su77, BG76], see [Bra18, Thm 2.1.10])).
- (i):
-
There is an adjunction ([Bor94, Sec. 3])

between the classical homotopy category of topological spaces (Definition A.16) and the opposite of the homotopy category of DGC-algebras (Definition A.19), where \(\mathcal {O}\) denotes the derived functor of forming the DGC-algebra of polynomial differential forms of a topological space.
- (ii):
-
This adjunction restricts to an equivalence of categories ([Bor94, Sec. 1])
 (90)
(90)between the rational homotopy category of connected nilpotent spaces of finite type (Definition A.18) and the homotopy category of connected DGC-algebras of finite type (Definition A.19).
- (iii):
-
Dropping the connectedness assumption on the left, this extends to an equivalence
 (91)
(91)with the category (89) on the right.
Example A.21
(Minimal DGC-algebra model for the n-spheres). Under the equivalence A.20 the minimal DGC-algebra models of the n-spheres are, up to isomorphism as follows:
- (i):
-
The minimal dgc-algebra model for the 0-sphere consists of two copies of the plain algebra of real numbers:
$$\begin{aligned} \mathcal {O}(S^0) \;=\; \mathrm {CE}(\mathfrak {l}(S^0)) := \{\mathbb {R}, \mathbb {R}\} \,. \end{aligned}$$(92) - (ii):
-
The minimal dgc-algebra model for the odd-dimensional spheres \(S^{2n+1}\) are
$$\begin{aligned} \mathcal {O}(S^{2n+1}) \;=\; \mathrm {CE}\left( \mathfrak {l}\left( S^{2n+1}\right) \right) := \mathbb {R}[ h_{2n+1} ]/ { \left( d h_{2n + 1} = 0 \right) }\;. \end{aligned}$$(93) - (iii):
-
The minimal dgc-algebra model for the positive even-dimensional spheres \(S^{2n+2}\) are
$$\begin{aligned} \mathcal {O}(S^{2n+2}) \;=\; \mathrm {CE}\left( \mathfrak {l}\left( S^4\right) \right) := \mathbb {R}[ \omega _{2n+2}, \omega _{4n+3} ]/ { \left( \begin{array}{l} d \omega _{2n+2} = 0 \\ d \omega _{4n+3} = - \tfrac{1}{2} \omega _{2n+2} \wedge \omega _{2n+2} \end{array}\right) }\;. \end{aligned}$$(94) - (iv):
-
Hence for \(k \in \mathbb {N}\), there is a canonical map
 (95)
(95)which represents a non-torsion homotopy class. For \(k \in \{0,1,3\}\) this is the (rational image of) the complex, quaternionnic, or octonionic Hopf fibration (Definition A.10), respectively.
Example A.22
(DG-Cocycles as maps in rational homotopy theory). Let
be the dgc-algebra (Definition A.19) whose underlying graded-commutative algebra is freely generated from a single generator in degree \(n+1\), and whose differential vanishes. Under the Sullivan equivalence (Proposition A.20) these are minimal models of the Eilenberg-MacLane spaces (Example A.25)
in that\(\mathcal {O}( B^{n+1} \mathbb {R} ) \simeq \mathrm {CE}( b^n \mathbb {R} )\). Then for \(A \in \mathrm {dgcAlg}\) any dgc-algebra, a dg-algebra homomorphism of the form

which, under the Sullivan equivalence (Proposition A.20), is a model for a map of spaces
is equivalently an element \(\mu \in A\) of degree \(n+1\), which is closed \(d \mu = 0 \; \in A\). Hence this is a cocycle in the cochain cohomology of the cochain complex underlying A.
Now under the Sullivan equivalence (Proposition A.20), the dgc-algebra on the right is a model for the Eilenberg-MacLane space \(K(\mathbb {R}, n+1)\)
and hence the dg-cocycle \(\mu \) is realized equivalently as map of spaces of the form

Example A.23
(DG-coboundaries as homotopies in rational homotopy theory). Let

be two dg-algebra homomorphisms as in Example A.22, hence equivalently two dg-cocycles of degree \(n+1\) in the given dgc-algebra A. Then a dg-homotopy between these homomorphisms is a dg-algebra homomorphism of the form

to the tensor product algebra of A with the de Rham algebra \(\Omega _{\mathrm {poly}}^{\bullet }([0,1])\) of polynomial differential forms on the unit interval, such that its restriction to the endpoints of the interval reproduces the given homomorphisms, respectively. Explicitly, if we write \(t \in \Omega ^0_{\mathrm {poly}}([0,1])\) for the canonical coordinate function, this means equivalently that \(\eta ^{*}\) corresponds to an element
of degree \(n+1\), such that \(d \eta = 0 \,\in A \otimes \Omega ^{\bullet }_{\mathrm {poly}}([0,1])\), hence such that
and satisfying \( \alpha (0) = \mu _0 \) and \( \alpha (1) = \mu _1 \). For example, if \(\omega \in A\) is a coboundary between the two cocycles, in the sense of the cochain cohomology of A
then we get such an \(\eta \) by setting
Therefore, under the Sullivan equivalence (Proposition A.20) a coboundary (97) between dg-cocycles corresponds to a homotopy (Definition 3.14) between the corresponding maps of spaces (96):

1.2.2 Cohomology
Our main interest in homotopy theories (Definition A.13) here is that each flavor of homotopy theory induces a corresponding generalized cohomology theory (Definition A.24 below). This includes Eilenberg-Steenrod-type generalized cohomology theories (Example A.25 below), which are often just called “generalized cohomology theories”, for short, but is in fact much more general than that: all kinds of differential and/or twisted and/or non-abelian and/or equivariant and/or orbifolded and/or ... concepts of cohomology theories arise via the simple Definition A.24 from a suitably chosen ambient homotopy theory (see [GS18a] for recent developments).
In the main text we are interested in this general concept of generalized cohomology in order to set up and study the cohomology theory equivariant rational cohomotopy of superspaces (Sect. 5).
Definition A.24
(Generalized cohomology theories from homotopy theory). Every homotopy theory induces a corresponding generalized cohomology theory: given a category with weak equivalences \((\mathcal {C}, W)\) (Definition A.13) and any object \(A \in \mathcal {C}\) then
-
a morphism \(c :X \rightarrow A\) in \(\mathcal {C}\) is an A-valued cocycle onX;
-
the equivalence relation on such morphisms induced by the localization functor (87) is the coboundary relation;
-
the image of \([c] := \gamma (c)\) in the morphisms of the homotopy category \(\mathrm {Ho}\left( \mathcal {C}[W]^{-1} \right) \) (Definition A.14) is the cohomology class of the cocycle.
Hence the set of A-valued cohomology classes on X is
Example A.25
(Examples of generalized cohomology theories). Examples of generalized cohomology theories arising from homotopy theories via Definition A.24 include the following:
-
For \((\mathcal {C}, W)\) the category of spectra with stable weak homotopy equivalences (see e.g. [Sch17c, Def. I.4.1]), the corresponding cohomology theories are equivalently the abelian generalized cohomology theories in the sense of the Eilenberg-Steenrod axioms. This is the statement of the Brown representability theorem (see e.g. [Sch17d, Sec. 1]). For instance
-
if \(A = \Sigma ^n H \mathbb {Z} \in \mathrm {Spectra}\) is an Eilenberg-MacLane spectrum (e.g. [Sch17c, Def. II.6.3]), then this is ordinary cohomology;
-
if
$$\begin{aligned} A := \mathrm {KU} := (\mathrm {KU}_k)_{k \in \mathbb {Z}} := \left\{ \begin{array}{ccc} B U \times \mathbb {Z} &{}\vert &{} k \; \text{ even } \\ U &{}\vert &{} k \; \text{ odd } \end{array} \right. \end{aligned}$$(98)this is K-theory (also called complex topological K-theory for emphasis, to distinguish from a wealth of variants, such as (100) below) which measure D-brane charge in type II string theory [Wi98, FrWi99, MoWi00, EvSa06, Evs06].
-
-
For \((\mathcal {C},W)\) the category of spaces with W the class of weak homotopy equivalences (Definition A.16), the corresponding cohomology theories are called non-abelian cohomology. For instance
-
if \(A = B G \in \mathrm {Spaces}\) is the classifying space of a topological group G, then the corresponding cohomology theory is nonabelian G-cohomology in degree 1, classifying G-principal bundles (in physics: G-instanton sectors);
-
if \(A = S^n \in \mathrm {Spaces}\) is an n-sphere, then the corresponding non-abelian cohomology theory is called cohomotopy [Spa49].
-
-
For \((\mathcal {C},W)\) the opposite category of dgc-algebras with W the class of quasi-isomorphisms (Definition A.19), we have that the corresponding cohomology theory is simply cochain cohomology of the underlying cochain complexes (see Example A.23 and Example A.22)
-
For \((\mathcal {C},W)\) the G-equivariant homotopy category (Definition 3.18) or the category of G-fixed point systems (Definition 3.25), whose homotopy categories are equivalent by Proposition 3.26, the corresponding cohomology theory is called Bredon equivariant cohomology, after [Bre67]. For instance:
-
For \((\mathcal {C},W)\) the G-equivariant stable homotopy category (of spectra with G-actions), the complex K-theory spectrum (98) equipped with \(\mathbb {Z}_2\)-action
 (100)
(100)where \(e \ne \sigma \in \mathbb {Z}_2\) acts by complex conjugation, represents the real cohomology theory (99) called real K-theory [At66, HuKr01], which measures D-brane charge in type I string theory, hence in type II string theory in the presence of O-planes, hence on orientifolds [Wi98, Sec. 5.2], [Guk99, Hor99, DFM09, DMR13]. See [GS18b] for recent advances in differential KO-theory.
Remark A.26
(Extra structure on cohomology). For a given coefficient object \(A \in \mathcal {C}\) in Definition A.24, the induced generalized cohomology \(H(-,A)\) a priori is only a set. This set inherits an extra algebraic structure to the extent that \(A \in \mathrm {Ho}\left( \mathcal {C}[W]^{-1} \right) \) is equipped with such extra structure. For instance, if A carries the structure of an (abelian) group in the homotopy category, then \(H(-,A)\) takes values in (abelian) cohomology groups. This is often considered by default. We highlight that this fails for key examples of cohomology theories, such as notably for cohomotopy theory (Example A.25), (except in those special degrees where the sphere coefficients happen to admit group structure). However, the minimum structure one will usually want to retain is that A is equipped with a point, namely with a morphism

in the homotopy category, from the terminal object \(*\), making it a “pointed object”. In this case the cohomology sets H(X, A) are also canonically pointed sets, namely by the unique cocycle \(X \rightarrow *\xrightarrow {\mathrm {pt}_A} A\) that factors through \(\mathrm {pt}_A\). This is then called the trivial cocycle, while all other cocycles are non-trivial.
Rights and permissions
About this article
Cite this article
Huerta, J., Sati, H. & Schreiber, U. Real ADE-Equivariant (co)Homotopy and Super M-Branes. Commun. Math. Phys. 371, 425–524 (2019). https://doi.org/10.1007/s00220-019-03442-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03442-3