Discontinuous Galerkin finite element heterogeneous multiscale method for advection–diffusion problems with multiple scales

Abstract

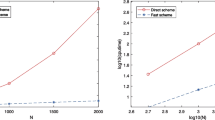
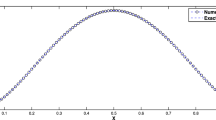
A discontinuous Galerkin finite element heterogeneous multiscale method is proposed for advection–diffusion problems with highly oscillatory coefficients. The method is based on a coupling of a discontinuous Galerkin discretization for an effective advection–diffusion problem on a macroscopic mesh, whose a priori unknown data are recovered from micro finite element calculations on sampling domains within each macro element. The computational work involved is independent of the high oscillations in the problem at the smallest scale. The stability of our method (depending on both macro and micro mesh sizes) is established for both diffusion dominated and advection dominated regimes without any assumptions about the type of heterogeneities in the data. Fully discrete a priori error bounds are derived for locally periodic data. Numerical experiments confirm the theoretical error estimates.

Appendix A: The effect of numerical integration for single scale DG-FEM

In this section, we study the influence of numerical integration for a single scale discontinuous Galerkin method. Without loss of generality we take the homogenized problem (4) as model problem for a single scale advection–diffusion problem. The single scale analysis presented in this section consists of two parts. First, we briefly comment on the analysis of the single scale DG-FEM without numerical quadrature used here for advection–diffusion problems, as it slightly differs from the method analyzed in [18] due to the choice of a different model problem. Second, we derive the stability and a priori results for the single scale DG-FEM with numerical quadrature defined in (49).

1.1 A.1 DG-FEM without numerical quadrature

For $v^H, w^H \in V^1(\Omega ,\mathcal{T }_H)$, let us introduce the bilinear form $B_0 = B_{D,0} + B_{A,0}$ by

$$\begin{aligned} \begin{aligned} B_{D,0}(v^H,w^H)&= \int _\Omega a^0(x) \nabla v^H(x) \cdot \nabla w^H(x)\,dx - \int _\Gamma \{a^0(s) \nabla v^H(s)\} \cdot [\![w^H ]\!]\,ds\\&\quad + \int _\Gamma \mu _S [\![v^H ]\!] \cdot [\![w^H ]\!]\,ds,\\ B_{A,0}(v^H,w^H)&= \int _\Omega b^0(x) \cdot \nabla v^H(x) \, w^H(x)\, dx - \int _\Gamma b^0(s) \cdot [\![v^H ]\!] w^H_{i_0(s)}\, ds, \end{aligned} \end{aligned}$$

(58)

with the penalty weighting function $\mu _S$ on an edge $e \in \mathcal{E }$ given by $\mu _S|_e = \alpha {\Vert {\{a^0(s)\}}\Vert }_\mathcal{F }H_e^{-1}$, where the penalization parameter $\alpha > 1$ is a positive parameter independent of the local mesh size and the data $a^0$, and the index $i_0(s)$ is discussed in Remark 3.2. We define $u^{0,H}$ as the solution of the variational problem: find $u^{0,H} \in V^1(\Omega ,\mathcal{T }_H)$ such that

$$\begin{aligned} B_0(u^{0,H}, v^H) = \int _\Omega f \, v^H\,dx \quad \forall \, v^H \in V^1(\Omega ,\mathcal{T }_H). \end{aligned}$$

(59)

Compared to the bilinear form $\tilde{B}_0$, defined in (48), the integrals are evaluated exactly in $B_0$, i.e., no numerical quadrature is used. Thus, the method given by (59) is free of any non-consistent perturbations and the Galerkin orthogonality holds

$$\begin{aligned} B_0(u^0-u^{0,H},v^H) = 0 \qquad \forall \, v^H \in V^1(\Omega ,\mathcal{T }_H). \end{aligned}$$

(60)

The stability of the method can be shown following the proof of Theorem 4.3 by setting $r_{vc,A} = 0$ (cf. Remark 5.10). Moreover, the a priori error estimate can be derived analogously to [18, Theorem 5.1], i.e., if $u^0 \in H^2(\Omega )$ then

$$\begin{aligned} {|||{u^0-u^{0,H}}|||} \le C (a_\infty ^{1/2} H + b_\infty ^{1/2} H^{3/2}) {|{u^0}|}_{H^2(\Omega )}. \end{aligned}$$

(61)

1.2 A.2 DG-FEM with numerical quadrature

In this section, we study the single scale DG-FEM based on the bilinear form $\tilde{B}_0$ given by (48).

Stability. The proof of the inf–sup condition for $\tilde{B}_0$ follows the proof of Theorem 4.3 by replacing $a^0_K$ and $b^0_K$ by $a^0(x_K)$ and $b^0(x_K)$, respectively, leading to

$$\begin{aligned} \tilde{r}_{vc,A} = \frac{1}{b_\infty } \sup _{\begin{array}{c} K \in \mathcal{T }_H \\ x \in K \end{array}} {|{b^0(x_K) - b^0(x)}|} + \frac{1}{b_\infty } \sup _{\begin{array}{c} e \in \mathcal{E }\\ x \in e \end{array}} {|{\{b^0(x_K)\} - b^0(x)}|}, \end{aligned}$$

This yields the same conditions A, B, C and D as in the proof of Theorem 4.3 with $r_{vc,A}$ replaced by ${\tilde{r}}_{vc,A}$.

A priori error estimate. Having shown the inf–sup condition for $\tilde{B}_0$ we derive the a priori error estimate for the single scale DG-FEM based on numerical integration used as estimate for the macro error $e_{mac}$.

Theorem A.1

Let $u^0 \in H^2(\Omega )$, $a^0 \in (W^{1,\infty }(\Omega ))^{d \times d}$ and $b^0 \in (W^{2,\infty }(\Omega ))^d$. Then the solution $\tilde{u}^{0,H}$ of the variational problem (49) satisfies the estimate

$$\begin{aligned} {|||{u^0 - \tilde{u}^{0,H}}|||} \le C {\left( {a_\infty ^{1/2} H + b_\infty ^{1/2} H^{3/2} + b_\infty ^{1/2} \min \{{{\mathrm{Pe}}}^{1/2} H^2, H\}}\right) } {\Vert {u^0}\Vert }_{H^2(\Omega )}, \end{aligned}$$

where $C$ is independent of $H$.

Proof

We combine the ideas of the proof of Theorem 4.6 and [18, Theorem 5.1]. We decompose the total error into two parts ${|||{u^0 - \tilde{u}^{0,H}}|||} \le {|||{u^0 - P_H u^0}|||} + {|||{P_H u^0 - \tilde{u}^{0,H}}|||}$ using the $L^2$ projection $P_H u^0$. Then, using the inf–sup condition for $\tilde{B}_0$, with stability constant $\tilde{\alpha }_S$, and the consistency (60) leads to

$$\begin{aligned} \tilde{\alpha }_S {|||{P_H u^0 - \tilde{u}^{0,H}}|||}&\le \sup _{w^H \in V^1(\Omega ,\mathcal{T }_H)} \frac{\tilde{B}_0(P_H u^0 - \tilde{u}^{0,H},w^H)}{{|||{w^H}|||}} \\&= \sup _{w^H \in V^1(\Omega ,\mathcal{T }_H)} \frac{\tilde{B}_0(P_H u^0,w^H) - B_0(u^{0,H},w^H)}{{|||{w^H}|||}} \\&= \sup _{w^H \in V^1(\Omega ,\mathcal{T }_H)} \frac{\tilde{B}_0(P_H u^0,w^H) - B_0(u^0,w^H)}{{|||{w^H}|||}}. \end{aligned}$$

Thus, we get the error decomposition

$$\begin{aligned} {|||{u^0 - \tilde{u}^{0,H}}|||} \le {}&{|||{u^0 - P_H u^0}|||} + \frac{1}{\tilde{\alpha }_S} \sup _{w^H \in V^1(\Omega ,\mathcal{T }_H)} \frac{B_0(P_H u^0 - u^0,w^H)}{{|||{w^H}|||}} \\&+ \frac{1}{\tilde{\alpha }_S} \sup _{w^H \in V^1(\Omega ,\mathcal{T }_H)} \frac{\tilde{B}_0(P_H u^0,w^H) - B_0(P_H u^0,w^H)}{{|||{w^H}|||}}, \end{aligned}$$

where the first two terms are identical to the error terms arising in the proof of (61) and the third term quantifies the effect of the numerical integration. Due to the decompositions $B_0 = B_{D,0} + B_{A,0}$ and $\tilde{B}_0 = \tilde{B}_{D,0} + \tilde{B}_{A,0}$ given by (58) and (48), respectively, we first estimate the difference $\tilde{B}_{D,0}(P_H u^0,w^H) - B_{D,0}(P_H u^0,w^H)$. Following the ideas of Lemma 5.12 we have

$$\begin{aligned}&{|{\tilde{B}_{D,0}(P_H u^0,w^H) - B_{D,0}(P_H u^0,w^H)}|}\nonumber \\&\quad \le C {\Vert {a^0}\Vert }_{W^{1,\infty }(\Omega )} H {\left( {{\Vert {\nabla P_H u^0}\Vert }^2_{L^2(\Omega )} + {|{P_H u^0}|}^2_{*,D}}\right) }^{1/2} {|||{w^H}|||}_D \nonumber \\&\quad \le C a_\infty ^{1/2} H {\Vert {u^0}\Vert }_{H^2(\Omega )} {|||{w^H}|||}_D. \end{aligned}$$

(62)

Next, we need to estimate $\tilde{B}_{A,0}(P_H u^0,w^H) - B_{A,0}(P_H u^0,w^H)$. Following Lemma 5.7 we obtain

$$\begin{aligned}&\left| \sum _{K \in \mathcal{T }_H} \int _K {\left( {b^0(x_K)-b^0(x)}\right) } \cdot \nabla P_H u^0 \, w^H\,dx\right| \nonumber \\&\quad \le C {\Vert {b^0}\Vert }_{W^{1,\infty }(\Omega )} H {\Vert {\nabla P_H u^0}\Vert }_{L^2(\Omega )} {\Vert {w^H}\Vert }_{L^2(\Omega )} \le C b_\infty ^{1/2} H {\Vert {u^0}\Vert }_{H^2(\Omega )} {|||{w^H}|||}_A. \end{aligned}$$

(63)

$$\begin{aligned}&\left| \int _\Gamma \{b^0(x_K)\} \cdot [\![P_H u^0 ]\!] w^H_{{\tilde{\textit{\i }}}_0}\,ds - \int _\Gamma b^0(s) \cdot [\![P_H u^0 ]\!] w^H_{i_0(s)}\,ds\right| \nonumber \\&\quad \le C \alpha ^{-1/2} \sup _{e \in \mathcal{E }, x \in e} {|{\{b^0(x_K)\} - b^0(x)}|} {|{P_H u^0 - u^0}|}_{*,D} {\Vert {w^H}\Vert }_{L^2(\Omega )} \nonumber \\&\quad \le C b_\infty ^{1/2} H^2 {|{u^0}|}_{H^2(\Omega )} {|||{w^H}|||}_A, \end{aligned}$$

(64)

where we used ${|{P_H u^0}|}_{*,D} = {|{P_H u^0 - u^0}|}_{*,D}$, as $H^2(\Omega ) \hookrightarrow C^0(\Omega )$ for $d \le 3$ and $u^0 = 0$ on $\partial \Omega$. If $b^0$ has the additional regularity $b^0 \in (W^{2,\infty }(\Omega ))^d$, we can improve estimate (63) using [23, Theorem 4]

$$\begin{aligned}&\left| \sum _{K \in \mathcal{T }_H} \int _K {\left( {b^0(x_K)-b^0(x)}\right) } \cdot \nabla P_H u^0 \, w^H\,dx\right| \nonumber \\&\quad \le C {\Vert {b^0}\Vert }_{W^{2,\infty }(\Omega )} H^2 {\Vert {\nabla P_H u^0}\Vert }_{L^2(\Omega )} {\Vert {\nabla w^H}\Vert }_{L^2(\Omega )} \nonumber \\&\quad \le C \frac{b_\infty }{a_\infty ^{1/2}} H^2 {\Vert {u^0}\Vert }_{H^2(\Omega )} {|||{w^H}|||}_D. \end{aligned}$$

(65)

Finally, combining estimates (62), (63), (64) and (65) allows to estimate the effect of the quadrature

$$\begin{aligned}&{|{\tilde{B}_0(P_H u^0,w^H) - B_0(P_H u^0,w^H)}|} \nonumber \\&\quad \le C {\left( {a_\infty ^{1/2} H + b_\infty ^{1/2} \min \{{{\mathrm{Pe}}}^{1/2} H^2, H\} + b_\infty ^{1/2} H^2}\right) } {\Vert {u^0}\Vert }_{H^2(\Omega )} {|||{w^H}|||}. \quad \end{aligned}$$

$\square$