1 Introduction

Many authors have employed a purely numerical treatment of the contribution of the ionosphere into GNSS range error, (Ashmanets et al. 1996; Strangeways and Ioannides 1999, 2002; Strangeways 2000; Strangeways and Nagarajoo 2005; Kashcheyev et al. 2012) in which the appropriate codes for direct numerical solution using the geometrical optics (GO) equations were developed, when assessing the errors of range measurements analytically. The perturbation theory has also been used in numerous papers (Hartmann and Leitinger 1984; Brunner and Gu 1991; Bassiri and Hajj 1992, 1993; Prokopov and Zanimonska 2005; Gherm et al. 2006; Kim and Tinin 2007; Hernandez-Pajares et al. 2007; Hoque and Jakowski 2008, 2011; Moore and Morton 2011; Petrie et al. 2011) when employing the GO equations. At transmission frequencies in the GHz band and higher, the squared ratio of the ionospheric electron plasma frequency to the transmission frequency is generally less than \(10^{-4}\), so that this ratio is a physically small parameter of the problem under consideration. The solution to the phase advance of the field determined in this way appears as a series with terms in inverse powers of the transmission frequency, and the integration of all the terms of this series is generally made along the (assumed) straight line-of-sight path of the propagating wave. The zero-order term corresponds to the true distance in free space (i.e., the phase distance along the straight line of sight in free space). The next term, of the order of the inverse squared frequency, represents the effect due to the slant TEC of the ionosphere along the same line of sight and the higher-order terms in the inverse powers of frequency account for the effects of the geomagnetic field, ray bending, etc.

If, however, the transmission frequency is somewhat lower (down to hundreds of MHz), then all the higher-order terms of the perturbation series give greater proportional contributions to the total ionospheric effect. In this case, it may be useful to develop a procedure which enables the explicit summing up of the contributions of the different terms of the inverse frequency powers in a closed form. Additionally, having this type of the solution available allows for explicit estimates of the contribution of the horizontal gradients of the electron density of the ionosphere into the propagation paths so that, for example, errors in GNSS range measurements can be determined.

In this paper, such a procedure will be presented. It will be based on the rigorous solution for the spherically layered ionosphere with any given vertical electron density profile as the zero-order approximation and with horizontal gradients of the electron density in the ionosphere taken into account, assuming the horizontal scales of electron density variations in the ionosphere to be much greater than the vertical ones. The solution, which will be produced below in this way, may be of importance, in particular, for the single-frequency mode of operation of the GNSS and its electron density correction (e.g., EGNOS, WAAS), as well as for other systems working in the VHF/UHF bands.

2 General relationships

As is widely accepted for the appropriate conditions, in the following treatment the dielectric permittivity \(\varepsilon _{o,e} \left( \mathbf{r} \right) \) (and the refractive index \(n_{o,e}^2 \left( \mathbf{r} \right) )\) of the normal ordinary and extraordinary magneto-ionic modes in the ionospheric cold collisionless plasma will be employed in the quasi-longitudinal approximation of the form:

$$\begin{aligned} \varepsilon _{o,e} \left( \mathbf{r} \right) =n_{o,e}^2 \left( \mathbf{r} \right) =1-\frac{\omega _{pl}^2 \left( \mathbf{r} \right) }{\omega ^{2}} \pm \frac{\omega _g \left( \mathbf{r} \right) \omega _{pl}^2 \left( \mathbf{r} \right) }{\omega ^{3}} \cos \chi \left( \mathbf{r} \right) . \end{aligned}$$
(1)

Here \(\omega _{pl} \left( \mathbf{r} \right) \) is the local plasma frequency in the ionosphere, \(\omega _g \left( \mathbf{r} \right) \) is the electron gyro-frequency, \(\omega \) is the transmission frequency, and \(\chi \) ( r ) is the angle between the Earth’s magnetic field and the wave normal direction. The characteristic spatial scales of the function \(\omega _{pl}^2 \left( \mathbf{r} \right) \) are defined by the vertical and horizontal scales of the ionospheric electron density changes, and the spatial scale of the gyro-frequency \(\omega _g \left( \mathbf{r} \right) \) is given by the spatial scale of the geomagnetic field.

Relationship (1) is an approximation of the more rigorous representation for the quasi-longitudinal approximation, which can be found in Budden (1985). This can be applied for the case of transmission frequencies of 100 MHz and higher which are considerably larger than the maximum electron gyro-frequencies of only about 1 MHz encountered in the terrestrial ionosphere.

When treating the effects of the anisotropy of the ionosphere in a rigorous manner, the “anisotropic” canonical ray path equations (see, e.g., in Kravtsov and Orlov 1980) should be utilized producing two different trajectories for the ordinary and extraordinary modes of propagation as follows:

$$\begin{aligned} \frac{{\hbox {d}}{} \mathbf{r}}{{\hbox {d}}\tau }= & {} \mathbf{p}-\frac{1}{2} \nabla _\mathbf{p} n_{o,e}^2 \left( {\mathbf{r,p}} \right) ,\nonumber \\ \frac{{\hbox {d}}{} \mathbf{p}}{{\hbox {d}}\tau }= & {} \frac{1}{2} \nabla _\mathbf{r} n_{o,e}^2 \left( {\mathbf{r,p}} \right) . \end{aligned}$$
(2)

However, numerous numerical calculations according to the technique developed in Gherm et al. (2006) show that, in order to provide sufficient accuracy of estimates of the full phase advance (of the order of \(10^{-12}\) m), it is sufficient to employ the isotropic ray path equations:

$$\begin{aligned} \frac{{\hbox {d}}{} \mathbf{r}}{{\hbox {d}}\tau }= & {} \mathbf{p} ,\nonumber \\ \frac{{\hbox {d}}{} \mathbf{p}}{{\hbox {d}}\tau }= & {} \frac{1}{2}\nabla \varepsilon \left( \mathbf{r} \right) \end{aligned}$$
(3)

with the “isotropic” dielectric permittivity

$$\begin{aligned} \varepsilon \left( \mathbf{r} \right) =n^{2}\left( \mathbf{r} \right) =1- X\left( {\mathbf{r} } \right) ; X\left( {\mathbf{r} } \right) =\frac{\omega _{pl}^2 \left( \mathbf{r} \right) }{\omega ^{2}} = \frac{e^{2}N\left( \mathbf{r} \right) }{m\varepsilon _0 \omega ^{2}} . \end{aligned}$$
(4)

If the independent variable \(\tau \) in (3) is changed according to the relationship

$$\begin{aligned} \sqrt{1- X\left( {\mathbf{r}\left( \tau \right) } \right) } {\hbox {d}}\tau = {\hbox {d}}s, \end{aligned}$$
(5)

this results in the other form of the isotropic ray paths equations, which will be employed below, as follows:

$$\begin{aligned} \frac{{\hbox {d}}{} \mathbf{r}}{{\hbox {d}}s}= & {} \frac{\mathbf{p}}{\sqrt{\varepsilon \left( \mathbf{r} \right) }} , \nonumber \\ \frac{{\hbox {d}}{} \mathbf{p}}{{\hbox {d}}s}= & {} \frac{\nabla \varepsilon \left( \mathbf{r} \right) }{2\sqrt{\varepsilon \left( \mathbf{r} \right) }}. \end{aligned}$$
(6)

Along with this, to perform integration along the given ray path, the anisotropic permittivity (1) will be utilized so that the phase advances for the ordinary and extraordinary modes are found according to the simplified formula

$$\begin{aligned}&\psi _{o,e} \left( {\mathbf{r}\left( s \right) } \right) \nonumber \\&\quad =\mathop {\int }\limits _{S_0 }^S {\sqrt{1- X\left( {\mathbf{r}\left( s \right) } \right) \pm \frac{\omega _g \left( {\mathbf{r}\left( s \right) } \right) }{\omega } X\left( {\mathbf{r}\left( s \right) } \right) \cos \chi \left( {\mathbf{r}\left( s \right) } \right) } {\hbox {d}}s} .\nonumber \\ \end{aligned}$$
(7)

Here, the integration is performed along the “isotropic” trajectories, governed by equations (6), and the permittivity of the ionospheric plasma is used, as given by the relationship (1). Equations (6, 7) will be utilized in the following treatment to assess the contribution of the ionosphere to the errors in the GNSS positioning. In equation (7), the ray path \(\mathbf{r}\left( s \right) \) is found when solving the ray equation (6).

3 Ray path equations and phase advance in the spherical coordinates

The following treatment will utilize the spherical coordinate system \({r} = \{r, \vartheta , \varphi \}\) with the origin placed at the Earth’s center and the polar axis directed to the end of the ray path (from the satellite) located on the Earth’s surface. In spherical coordinates, the gradient of the dielectric permittivity on the right-hand side of the second equation in (6) has the form:

$$\begin{aligned} \nabla \varepsilon \left( {r,\vartheta ,\varphi } \right) = \frac{1}{h_r }\frac{\partial \varepsilon }{\partial r} \mathbf{e}_r + \frac{1}{h_\vartheta } \frac{\partial \varepsilon }{\partial \vartheta } \mathbf{e}_\vartheta + \frac{1}{h_\varphi } \frac{\partial \varepsilon }{\partial \varphi } \mathbf{e}_\varphi . \end{aligned}$$
(8)

Here

$$\begin{aligned} h_r \left( r \right) = 1, h_\vartheta \left( r \right) = r, h_\varphi \left( {r,\vartheta } \right) = r\sin \vartheta \end{aligned}$$
(9)

are the Lame coefficients for the spherical coordinate system. Ray path equations written in the spherical coordinates can be found, e.g., in Haselgrove (1955), or Kravtsov and Orlov (1990).

In equation (6), written in the spherical coordinates, it is convenient to employ the scalar variable r of the spherical coordinate system as the new independent variable in the ray path equations instead of s, utilizing the relationship:

$$\begin{aligned} {\hbox {d}}s = {\hbox {d}}r\sqrt{1 + h_\vartheta ^2 \left( r \right) \left( {\frac{{\hbox {d}}\vartheta }{{\hbox {d}}r}} \right) ^{2} + h_\varphi ^2 \left( r \right) \left( {\frac{{\hbox {d}}\varphi }{{\hbox {d}}r}} \right) ^{2}} \end{aligned}$$
(10)

and the eikonal equation, also written in the spherical coordinates, for the eikonal \(\psi _i \), corresponding to the isotropic system (6), as:

$$\begin{aligned} p_r^2 + \frac{1}{h_\vartheta ^2 \left( r \right) } p_\vartheta ^2 + \frac{1}{h_\varphi ^2 \left( {r,\vartheta } \right) } p_\varphi ^2 = \varepsilon \left( {r,\vartheta ,\varphi } \right) , \end{aligned}$$
(11)

where the momentum p has the components \( p_r =\frac{\partial \psi _i }{\partial r} , p_\vartheta =\frac{\partial \psi _i }{\partial \vartheta } , p_\varphi =\frac{\partial \psi _i }{\partial \varphi }\).

Then, six scalar equations in (6) are reduced to the following four scalar equations for the four scalar functions, which are two angle functions \(\vartheta (r)\), \(\varphi (r)\) and two angle momenta \(p_{\vartheta }(r)\), \(p_{\varphi }(r)\):

$$\begin{aligned}&r\frac{\partial \vartheta }{\partial r}=\frac{1}{r\sqrt{\varepsilon }}p_\vartheta \sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^{2}\left( {\frac{{\hbox {d}}\varphi }{{\hbox {d}}r}} \right) ^{2}} \nonumber \\&r\sin \vartheta \frac{\partial \varphi }{\partial r}=\frac{1}{r\sqrt{\varepsilon }\sin \vartheta }p_\varphi \sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^{2}\left( {\frac{{\hbox {d}}\varphi }{{\hbox {d}}r}} \right) ^{2}} \nonumber \\&\frac{\partial p_\vartheta }{\partial r}=\left( {\frac{\partial \sqrt{\varepsilon }}{\partial \vartheta }+\frac{1}{\sqrt{\varepsilon }}\left( {\frac{\cos \vartheta }{r^{2}\sin ^{3}\vartheta }p_\varphi ^2 } \right) } \right) \nonumber \\&\qquad \times \,\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^{2}\left( {\frac{{\hbox {d}}\varphi }{{\hbox {d}}r}} \right) ^{2}} \nonumber \\&\frac{\partial p_\varphi }{\partial r}=\frac{\partial \sqrt{\varepsilon }}{\partial \varphi }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^{2}\left( {\frac{{\hbox {d}}\varphi }{{\hbox {d}}r}} \right) ^{2}} \end{aligned}$$
(12)

Finally, the momentum \(p_{r }(r)\) can be found, whenever necessary, from the eikonal equation in the form:

$$\begin{aligned}&p_r \left( r \right) \nonumber \\&\quad =\sqrt{\varepsilon \left( {r,\vartheta \left( r \right) ,\varphi \left( r \right) } \right) - \frac{1}{h_{^{\vartheta }}^2 \left( r \right) } \left( {p_\vartheta \left( r \right) } \right) ^{2} - \frac{1}{h_{^{\varphi }}^2 \left( {r,\vartheta \left( r \right) } \right) }\left( {p_\varphi \left( r \right) } \right) ^{2} } .\nonumber \\ \end{aligned}$$
(13)

Once equation (12) has been solved, the phase advances for the two magneto-ionic modes, according to (7), can be expressed as:

$$\begin{aligned}&\psi _{o,e} \left( {\mathbf{r}\left( r \right) } \right) =\mathop {\int }\limits _{R_E }^r \sqrt{1 + r^{2}\left( {\frac{{\hbox {d}}\vartheta \left( r \right) }{{\hbox {d}}r}} \right) ^{2} + r^{2}\sin ^{2}\vartheta \left( r \right) \left( {\frac{{\hbox {d}}\varphi \left( r \right) }{{\hbox {d}}r}} \right) ^{2}} \nonumber \\&\quad \cdot \sqrt{1- X\left( {r,\vartheta \left( r \right) ,\varphi \left( r \right) } \right) \pm \frac{\omega _g \left( {r,\vartheta \left( r \right) ,\varphi \left( r \right) } \right) }{\omega } X\left( {r,\vartheta \left( r \right) ,\varphi \left( r \right) } \right) \cos \chi \left( {r,\vartheta \left( r \right) ,\varphi \left( r \right) } \right) } {\hbox {d}}r . \end{aligned}$$
(14)

4 Perturbation theory for ray path equations and phase advances

The treatment of the propagation problem here will not be confined to the spherically symmetric ionosphere. On the other hand, obviously, no comprehensive solution to the rigorous path equations (12) can be constructed analytically in an explicit form and so reasonable approximations must be used to produce any analytic results.

It is also worth mentioning that similar equations to (12), written in rectangular coordinates, have been considered by Kim and Tinin (2007) employing the perturbation theory. In the perturbation theory developed by these authors, as well as in many papers by other authors quoted in Introduction, the small parameter of the problem is X(r). The main term of this perturbation theory corresponds to the phase advance in free space, so that the series obtained is the expansion in inverse frequency. In the series expansion, the integration of all the terms is made along the straight line-of-sight path. By contrast, as was mentioned in Introduction and is stressed again here, in the present treatment X(r) formally is not the small parameter of the problem and the square root for \(\varepsilon \left( \mathbf{r} \right) \) is not expanded in a series of the powers of X(r) (or the inverse powers of frequency).

When constructing the perturbation theory for small horizontal gradients of the electron density of the ionosphere, it can be assumed (from extensive experimental observations) that the angle (horizontal) components of the gradient of the dielectric permittivity in (8) are small as compared to the vertical gradient, so that the formal small parameters of the problem, as are commonly employed in mathematical physics, are given by the following relationships:

$$\begin{aligned} \alpha _\vartheta =\frac{\frac{\Delta \varepsilon }{h_\vartheta \left( r \right) \Delta \vartheta }}{\frac{\Delta \varepsilon }{\Delta r}} = \frac{L_r }{L_\vartheta }< 1, \alpha _\varphi =\frac{\frac{\Delta \varepsilon }{h_\varphi \left( {r,\vartheta } \right) \Delta \varphi }}{\frac{\Delta \varepsilon }{\Delta r}} = \frac{L_r }{L_\varphi } < 1 . \end{aligned}$$
(15)

In (15), the vertical scale of the ionosphere \( L_r \) and two generally different angle (horizontal) scales \( L_\vartheta \) and \( L_\varphi \) (with the dimension of distance because of the appropriate Lame coefficients) are introduced.

It should be additionally mentioned that, as will be clear from the following results presented below, the expansion of the phase advance in terms of the horizontal gradients of the electron density appears as the expansion in small parameters \( \frac{\partial \varepsilon }{\partial \vartheta } , \frac{\partial \varepsilon }{\partial \varphi }\), which are really much smaller than the formal parameters introduced in (15) due to the small ratio of the maximum value of the plasma frequency to the transmission frequency.

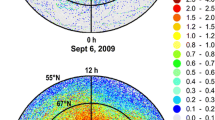
The typical value of the vertical characteristic scale of the background ionosphere \({{L}_{r}}\) is of the order of 100 Km for the bottom side ionosphere and slightly larger for the top side. Hoque and Jakowski (2008), when modeling the ionosphere by a Chapman layer, used vertical ionospheric electron density Chapman profiles with scale heights of \(H = 60\)–80 km. The estimates of the horizontal gradient scales can be derived from any standard ionospheric model, e.g., IRI (Bilitza et al. 2014) or NeQuick (Nava et al. 2008). The typical values of the angle derivatives of the electron density, which will be introduced in detail in Sects. 6 and 6.1, are of the order of \(-0.01\) inverse degrees (outside the equatorial anomaly, see Fig. 1), whereas for the region of the equatorial anomaly, the north–south derivative can reach a value of the order of \(-0.1\) (as in the equatorial anomaly shown in Fig. 1). The corresponding characteristic spatial scale of the anomaly is of the order of a few thousand kilometers, whereas outside the region of the anomaly, the spatial scales are estimated to be several thousand kilometers. All these estimates finally show that parameters \(\frac{\partial \varepsilon }{\partial \vartheta } , \frac{\partial \varepsilon }{\partial \varphi }\) mentioned above are really small parameters of the problem. These are of the order of \(10^{-5 }\) in the case of the higher frequency (1575 MHz) and \(10^{-3}\) in the worst case for the lower frequency (150 MHz).

Fig. 1
figure 1

Ionospheric electron density near the height of its maximum (369 km) as given by the IRI model on January 27, 2003, at 13.30 LT

Full size image

If the inequalities (15) hold, the solution to the equations (12) can be sought for as the perturbation series in powers of small horizontal gradients of the ionospheric permittivity as given by:

$$\begin{aligned}&\vartheta \left( r \right) =\vartheta _0 \left( r \right) + \vartheta _1 \left( r \right) + ... , \nonumber \\&\varphi \left( r \right) = \varphi _0 \left( r \right) + \varphi _1 \left( r \right) + ... , \nonumber \\&p_\vartheta \left( r \right) = p_{\vartheta 0} \left( r \right) + p_{\vartheta 1} \left( r \right) + ... , \nonumber \\&p_\varphi \left( r \right) = p_{\varphi 0} \left( r \right) + p_{\varphi 1} \left( r \right) + ... . \end{aligned}$$
(16)

The numbers of the terms in series (16) denote the order of their small sizes in terms of the small parameters introduced by (15). Obviously, the zero-order terms in (16) correspond to the solution for the spherically symmetric ionosphere with the curved paths of propagation corresponding to the spherically symmetric case. It will also automatically sum up in closed form all the inverse frequency powers of the traditional expansion. The next order approximations in (16) will be found by the appropriate integration along the curved paths of propagation corresponding to the spherically symmetric ionosphere. It will be shown below that the series constructed in this way converge much faster compared with the perturbation theory where integration is performed along the straight line paths.

4.1 Solution to the ray paths

As was mentioned, in the perturbation series (16), the zero-order functions \(\{ \vartheta _{0}(r)\), \(\varphi _{0}(r)\); \(p_{\vartheta 0}(r)\), \(p_{\varphi 0}(r)\}\) correspond to the well-known solution for the spherically layered (spherically symmetric) ionosphere with any given vertical profile of the permittivity (determined by the ionospheric electron density vertical profile). The equations for these functions are well known (see, e.g., Kravtsov and Orlov 1990), and they are given as follows:

$$\begin{aligned}&\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}=\frac{p_{\vartheta _0 } }{r^{2}\left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}-\frac{p_{\phi _0 }^2 }{r^{2}\sin ^{2}\vartheta _0 \left( r \right) }} \right) ^{1/2}}, \nonumber \\&\frac{{\hbox {d}}\phi _0 }{{\hbox {d}}r}=\frac{p_{\phi _0 } }{r^{2}\sin ^{2}\vartheta _0 \left( r \right) \left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}-\frac{p_{\phi _0 }^2 }{r^{2}\sin ^{2}\vartheta _0 \left( r \right) }} \right) ^{1/2}}, \nonumber \\&\frac{{\hbox {d}}p_{\vartheta _0 } }{{\hbox {d}}r}=0, \nonumber \\&\frac{{\hbox {d}}p_{\phi _0 } }{{\hbox {d}}r}=0. \end{aligned}$$
(17)

Here, the constant \(\tilde{\vartheta }\) was introduced to indicate the angle coordinate between the receiver and transmitter, where the vertical profile for the zero-order spherically symmetric ionosphere is specified. In the following consideration, three different options will be explored, which are: \(\tilde{\vartheta }=0\) corresponding to the profile taken above the receiver; \(\tilde{\vartheta }=\vartheta _{pp} \) corresponding to the vertical profile at the pierce point (the point where the straight line between a receiver and a satellite crosses the height of the maximum of the electron density of the ionosphere); and, finally, \(\tilde{\vartheta }=\vartheta _s \) for the vertical profile specified below satellite.

The explicit solution to these equations written in the spherical coordinates (chosen in such a way that the polar axis from the origin passes through the point of observation, located on the Earth’s surface, and the variable \(\varphi \) is measured starting from the plane, containing the origin, observation point and satellite) is given by:

$$\begin{aligned}&p_{\varphi 0} ={\hbox {const}}=0 \nonumber \\&\varphi _0 ={\hbox {const}}=0 \nonumber \\&p_{\vartheta _0 } ={\hbox {const}} \nonumber \\&\vartheta _0 \left( r \right) =p_{\vartheta _0 } \mathop {\int }\limits _{R_e }^r {\frac{{\hbox {d}}r}{r\sqrt{\varepsilon \left( {r,\tilde{\vartheta },0} \right) r^{2}-p_{\vartheta _0 } ^{2}}}} \end{aligned}$$
(18)

Here, the constant \(p_{\vartheta _0 } \) is the impact parameter for the ray path in the spherically symmetric case for the path starting from the point \(\left( {R_e ,0,0} \right) \) and arriving at the location of a satellite \(\left( {R_s ,\vartheta _s ,0} \right) \). Constant \(p_{\vartheta _0 } \) is defined from the last of the relations (18) with \(\vartheta _0 \left( {R_s } \right) =\vartheta _s \) and \(r=R_s\) at upper limit of integration. Then, this becomes the algebraic transcendent equation for the parameter \(p_{\vartheta _0 } \), which is solved numerically. To accomplish this, a numerical procedure has been developed to solve the homing-in problem for the spherically symmetric ionosphere. In this procedure, the numerical algorithm for solving implicit equations was employed (see Brent 1973), based on a combination of bisection, secant, and inverse quadratic interpolation methods.

The spherically symmetric case was considered by many authors (see, e.g., Strangeways and Ioannides 2002; Hoque and Jakowski 2008; Petrie et al. 2011). In the present consideration, however, this is only the zero-order term, which already takes into account all the ionospheric effects of the spherically symmetric ionosphere, whereas the higher-order corrections take account of the effects due to the horizontal (here angular) gradients of the electron density in the ionosphere. For the first-order correction due to the horizontal gradients of the ionospheric electron density, which will be discussed in the next subsection, integration is performed along the curved paths of propagation in the spherically symmetric ionosphere, defined by (18). In this type of integration, all the inverse frequency ionospheric effects in the traditional treatment are taken into account automatically at each step, including that of zero-order. Any term of the series (16) can be re-arranged in terms of the traditional different-order effects by additionally expanding each into a series of powers of the inverse frequency and can be easily accomplished if necessary.

4.2 The first-order corrections to the ray paths

The first-order corrections in the series from (16) are obtained from the equations

$$\begin{aligned}&\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}=\frac{p_{\vartheta _0 }^2 p_{\vartheta _1 } \left( r \right) }{r^{4}\left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{3/2}}\nonumber \\&\qquad \qquad -\frac{1}{2}\cdot \frac{p_{\vartheta _0 } \frac{\partial \varepsilon }{\partial \vartheta }\left| {_{\left( {r,\tilde{\vartheta },0} \right) } \cdot \vartheta _0 \left( r \right) } \right. }{r^{2}\left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{3/2}}\nonumber \\&\qquad \qquad +\frac{p_{\vartheta _1 } \left( r \right) }{r^{2}\left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{1/2}} \nonumber \\&\frac{{\hbox {d}}\phi _1 }{{\hbox {d}}r}=\frac{p_{\phi _1 } \left( r \right) }{r^{2}\sin ^{2}\vartheta _0 \left( r \right) \cdot \left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{1/2}} \nonumber \\&\frac{{\hbox {d}}p_{\vartheta _1 } }{{\hbox {d}}r}=\frac{1}{2\cdot \left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{1/2}}\frac{\partial \varepsilon \left( {r,\vartheta ,0} \right) }{\partial \vartheta }\left| {_{\vartheta =\tilde{\vartheta }} } \right. \nonumber \\&\frac{{\hbox {d}}p_{\phi _1 } }{{\hbox {d}}r}=\frac{1}{2\cdot \left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) -\frac{p_{\vartheta _0 }^2 }{r^{2}}} \right) ^{1/2}}\frac{\partial \varepsilon \left( {r,\tilde{\vartheta },\phi } \right) }{\partial \phi }\left| {_{\phi =0} } \right. \nonumber \\ \end{aligned}$$
(19)

The general solutions to equations (19) are:

$$\begin{aligned}&{\vartheta }_{1}(r)=\mathop {\int }\limits _{\mathrm{Re}}^{r}\left( \frac{P_{\vartheta _{0}}^{2} P_{\vartheta _{1}}(r^{\prime })}{r^{\prime 4}\left( \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0\right) -\frac{P_{{\vartheta }_{0}}^2}{r^{\prime 2}}\right) ^{3/2}}\right. \nonumber \\&\qquad \qquad -\frac{1}{2}. \frac{P_{\vartheta _{0}}\frac{\partial \varepsilon }{\partial \vartheta }\vert _{(r,\tilde{\vartheta }, 0)}. {\vartheta }_{0} (r^{\prime })}{r^{\prime 2}\left( \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0\right) - \frac{P_{{\vartheta }_{0}}}{r^{\prime 2}}\right) ^{3/2}}\nonumber \\&\qquad \qquad \left. +\frac{P_{\vartheta _{1}}(r^{\prime })}{r^{\prime 2 }\left( \varepsilon \left( r^{\prime } ,\tilde{\vartheta }, 0\right) - \frac{P_{\vartheta _{0}}^2}{r^{\prime 2}} \right) ^{1/2}}\right) {{\hbox {d}}r}^\prime + C_1\nonumber \\&{\varphi }_{1}(r)=\mathop {\int }\limits _{\mathrm{Re}}^{r} \left( \frac{P_{\varphi _1}(r^{\prime })}{r^2 {\hbox {sin}}^2 {\vartheta }_0(r^{\prime })\left( \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0 \right) -\frac{P_{\vartheta _0}}{r^{\prime 2}} \right) ^{1/2}}\right) {{\hbox {d}}r}^{\prime }+ C_2\nonumber \\&P_{\vartheta _1}(r)= \mathop {\int }\limits _{\mathrm{Re}}^{r} \frac{1}{2\left( \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0\right) - \frac{P_{\vartheta _0}^2}{r^{\prime 2}}\right) ^{1/2}}\frac{\partial \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0\right) }{\partial \vartheta }\vert _{\vartheta =\tilde{\vartheta }} {{\hbox {d}}r}^{\prime }+ C_3\nonumber \\&P_{\varphi _1}(r)=\mathop {\int }\limits _{\mathrm{Re}}^{r} \frac{1}{2\left( \varepsilon \left( r^{\prime }, \tilde{\vartheta }, 0\right) -\frac{P_{\vartheta }^{2}}{r^{\prime 2}}\right) ^{1/2}} \frac{\partial \varepsilon \left( r^{\prime }, \tilde{\vartheta }, \varphi \right) }{\partial \varphi }\vert _{\varphi =0} {{\hbox {d}}r}^{\prime }+ C_4\nonumber \\ \end{aligned}$$
(20)

where the four constants are found from the conditions at the communicating points as follows:

$$\begin{aligned} \vartheta _1 \left( {R_e } \right)= & {} 0, \nonumber \\ \vartheta _1 \left( {R_s } \right)= & {} 0, \nonumber \\ \phi _1 \left( {R_e } \right)= & {} 0, \nonumber \\ \phi _1 \left( {R_s } \right)= & {} 0. \end{aligned}$$
(21)

The explicit representations of the solutions \(\left\{ {\vartheta _1 \left( r \right) ,\varphi _1 \left( r \right) } \right\} \) for the first-order corrections to the ray paths are given in Appendix (equations (42, 46)). Actually, this solves the homing-in problem for the spherically non-symmetric ionosphere in terms of the first-order corrections taking account of the horizontal gradients. Then, the first-order corrections to the ray paths are calculated numerically according to the explicit equations (42, 46).

Representations (18) and (20), with the constants determined according to the equations given in Appendix, will be employed to determine the phase advances (14) taking account of the effects of the horizontal gradients up to second order in small parameters of the angular dependencies of the permittivity of the ionosphere.

4.3 The series for phase advance

To obtain the representation for the phase advance taking account of the first- and second order in terms of small parameters (15), it is sufficient, as will be shown below, to account for the first-order corrections to the spherically symmetric trajectories, so that the equation (14) is reproduced in the following form:

$$\begin{aligned} \psi \left( {\mathbf{r}\left( S \right) } \right)= & {} \mathop {\int }\limits _{R_e }^{R_s } \sqrt{\varepsilon _{o,e} \left( {r,\vartheta _0 \left( r \right) +\vartheta _1 \left( r \right) ,\varphi _1 \left( r \right) } \right) }\nonumber \\&\times \,\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}+\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^{2}\left( {\frac{{\hbox {d}}\varphi _1 }{{\hbox {d}}r}} \right) ^{2}}{\hbox {d}}r .\nonumber \\ \end{aligned}$$
(22)

Here \(\varepsilon _{o,e} \left( \mathbf{r} \right) \) is given by equation (1).

Regarding equation (22), two different modes of operation can be applied in the following consideration. When dealing with relatively small horizontal gradients (e.g., for the paths of propagation far from the equatorial anomalies), the horizontal dependence of the dielectric permittivity may be treated as uniformly slow for all the elevation angles of paths of propagation. In this case, the expansion of the dielectric permittivity in horizontal (angle) variables can be performed relative to the limiting cases of the zero-order spherical ionosphere taken either above the receiver on the Earth’s surface, or below the satellite (the same for any elevation angle). Thus, the reference can be a spherically symmetric ionosphere corresponding to everywhere either the ionosphere above the receiver on the ground or the one below the satellite. Of course the ionosphere at any chosen intermediate point (such as the midpoint of the path) could be chosen as the reference if desired.

For these two cases, expanding the square roots in the integrand of (22) in series of powers of the angle variables \(\vartheta _1 \), \(\varphi _1 \) and taking account of the first- and second-order terms, yields the phase advance as the sum of the following three terms:

$$\begin{aligned} \psi \left( \mathbf{r} \right) = \psi _0 \left( \mathbf{r} \right) + \psi _1 \left( \mathbf{r} \right) +\psi _2 \left( \mathbf{r} \right) . \end{aligned}$$
(23)

Here the zero-order term represents the phase advance along the curved path in the spherically symmetric ionosphere, taken as above the receiver at \(\tilde{\vartheta }=0\):

$$\begin{aligned} \psi _{0r} \left( {\mathbf{r}\left( L \right) } \right) =\mathop {\int }\limits _{R_e }^{R_s } {\sqrt{\varepsilon \left( {r,0,0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}{\hbox {d}}r} , \end{aligned}$$
(24)

or below the transmitter on a satellite at \(\vartheta _{s}\):

$$\begin{aligned} \psi _{0s} \left( {\mathbf{r}\left( L \right) } \right) =\mathop {\int }\limits _{R_e }^{R_s } {\sqrt{\varepsilon \left( {r,\vartheta _{s},0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}{\hbox {d}}r} , \end{aligned}$$
(25)

The first-order term in (23) is the main order correction due to the horizontal gradient of the electron density of the ionosphere, written as

$$\begin{aligned}&\psi _{1r} \left( {\mathbf{r}\left( L \right) } \right) \nonumber \\&\quad =\mathop {\int }\limits _{R_e }^{R_s } \sqrt{\varepsilon \left( {r,0,0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}\nonumber \\&\qquad \times \left( {\frac{h_\vartheta ^{2}\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}}{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}+\frac{\vartheta _0 \left( r \right) }{2\varepsilon }\frac{\partial \varepsilon \left( {r,\vartheta ,0} \right) }{\partial \vartheta }\left| {_{\left( {r,0,0} \right) } } \right. } \right) {\hbox {d}}r ,\nonumber \\ \end{aligned}$$
(26)

for the zero-order ionosphere taken above the receiver; and

$$\begin{aligned}&\psi _{1s} \left( {\mathbf{r}\left( L \right) } \right) \nonumber \\&\quad =\mathop {\int }\limits _{R_e }^{R_s } \sqrt{\varepsilon \left( {r,\vartheta _{s} ,0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}\nonumber \\&\qquad \times \left( {\frac{h_\vartheta ^{2}\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}}{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}+\frac{\left( {\vartheta _0 \left( r \right) -\vartheta _{s}} \right) }{2\varepsilon }\frac{\partial \varepsilon \left( {r,\vartheta ,0} \right) }{\partial \vartheta }\left| {_{\left( {r,\vartheta _{s} ,0} \right) } } \right. } \right) {\hbox {d}}r ;\nonumber \\ \end{aligned}$$
(27)

for the zero-order ionosphere taken below the appropriate satellite.

Finally, the second-order correction in the angle variables in (23) in the first case is represented as:

$$\begin{aligned}&\psi _2 \left( {r\left( L \right) } \right) \nonumber \\&\quad =\mathop {\int }\limits _{R_e }^{R_{s} } \sqrt{\varepsilon \left( {r,\tilde{\vartheta },0} \right) }\cdot \sqrt{1+h_\vartheta ^2 \left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}\cdot \left( \frac{\left( {\vartheta _0 } \right) ^{2}}{4\varepsilon \left( {r,\tilde{\vartheta },0} \right) }\right. \nonumber \\&\qquad \left. \cdot \frac{\partial ^{2}\varepsilon \left( {r,\vartheta ,\varphi } \right) }{\partial \vartheta ^{2}}\left| {_{\left( {r,\tilde{\vartheta },0} \right) } } \right. + \right. \frac{1}{2\varepsilon \left( {r,\vartheta _0 ,0} \right) } \nonumber \\&\qquad \cdot \frac{\partial \varepsilon \left( {r,\vartheta ,\varphi } \right) }{\partial \vartheta }\left| {_{\left( {r,\tilde{\vartheta },0} \right) } \cdot \vartheta _1 \left( r \right) } \right. +\frac{1}{2\varepsilon \left( {r,\vartheta _0 ,0} \right) }\nonumber \\&\qquad \cdot \frac{\partial \varepsilon \left( {r,\vartheta ,\varphi } \right) }{\partial \varphi }\left| {_{_{\left( {r,\tilde{\vartheta },0} \right) } } \cdot \varphi _1 \left( r \right) +\frac{1}{2}\frac{h_\vartheta ^2 \left( {\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}} \right) ^{2}+h_\varphi ^2 \left( {\frac{{\hbox {d}}\varphi _1 }{{\hbox {d}}r}} \right) ^{2}}{1+h_\vartheta ^2 \left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}} \right. \nonumber \\&\qquad -\frac{1}{2}\frac{h_\vartheta ^4 \left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}\cdot \frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}} \right) ^{2}}{\left( {1+h_\vartheta ^2 \left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}} \right) ^{2}}+\left. \frac{\vartheta _0 }{2\varepsilon \left( {r,\tilde{\vartheta },0} \right) }\cdot \frac{\partial \varepsilon \left( {r,\vartheta ,\varphi } \right) }{\partial \vartheta }\left| _{\left( {r,\tilde{\vartheta },0} \right) } \right. \right. \nonumber \\&\qquad \left. \left. \cdot \frac{h_\vartheta ^2 \frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}\cdot \frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}}{1+h_\vartheta ^2 \left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}-\frac{\left( {\vartheta _0 } \right) ^{2}}{8\left( {\varepsilon \left( {r,\tilde{\vartheta },0} \right) } \right) ^{2}}\left( {\frac{\partial \varepsilon \left( {r,\vartheta ,\varphi } \right) }{\partial \vartheta }\left| {_{\left( {r,\tilde{\vartheta },0} \right) } } \right. } \right) ^{2} \right. \right) {\hbox {d}}r\nonumber \\ \end{aligned}$$
(28)

or in similar form with the appropriate alterations of the angle variables for the two other cases. They are not explicitly presented here in order to save space. These integrals are calculated numerically, once the zero-order vertical ionosphere profile at the pierce point and the horizontal gradients along this vertical line are specified.

The identical first two factors in the integrands in all the terms in (24, 26, 28) and (25, 28) show that calculations are actually performed along the curved ray paths corresponding to the spherically symmetric ionosphere. It should additionally be noted that the first-order contribution to the phase advance (27, 28) contains solely the \(\vartheta \)-component of the horizontal gradient of the ionospheric electron density. (Note that our spherical coordinate system is not a geographical coordinate system but it is associated with the plane containing the Earth’s center, the satellite and the receiver.)

Alternatively, in the conditions of fairly strong horizontal gradients of the electron density of the ionosphere, another variant of the perturbation theory should be introduced, where the zero-order spherically symmetric ionosphere is chosen locally for each elevation angle of the path of propagation from a satellite to the point of observation on the Earth’s surface to produce the zero-order rigorous solution for the spherically layered ionosphere. In the following calculations, such a “zero-order” ionosphere will be utilized as existing at the appropriate pierce point \(\vartheta _{pp} \), at the electron density maximum, for each given elevation angle of a satellite, so that

$$\begin{aligned}&\psi _{0p} \left( {\mathbf{r}\left( L \right) } \right) =\mathop {\int }\limits _{R_e }^{R_s } {\sqrt{\varepsilon \left( {r,\vartheta _{pp} ,0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}{\hbox {d}}r} , \end{aligned}$$
(29)
$$\begin{aligned}&\psi _{1p} \left( {\mathbf{r}\left( L \right) } \right) \nonumber \\&\quad =\mathop {\int }\limits _{R_e }^{R_s } \sqrt{\varepsilon \left( {r,\vartheta _{pp} ,0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}\nonumber \\&\qquad \times \left( {\frac{h_\vartheta ^{2}\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}\frac{{\hbox {d}}\vartheta _1 }{{\hbox {d}}r}}{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 }{{\hbox {d}}r}} \right) ^{2}}+\frac{\left( {\vartheta _0 \left( r \right) -\vartheta _{pp} } \right) }{2\varepsilon }\frac{\partial \varepsilon \left( {r,\vartheta ,0} \right) }{\partial \vartheta }\left| {_{\left( {r,\vartheta _{pp} ,0} \right) } } \right. } \right) {\hbox {d}}r .\nonumber \\ \end{aligned}$$
(30)

Such a choice, as will be shown, provides a negligibly small contribution of the second-order term in (23) even for the largest values of the horizontal gradients of the electron density observable in the real ionosphere even in the case of extremely slant paths of propagation at GHz frequencies. The true distance (phase advance in vacuum) between the communicating points (transmitter and receiver) is provided by each of the equations (24, 25) in the case of \(\varepsilon \left( {r,\vartheta ,\varphi } \right) = 1\).

Below the method of calculation of the phase advance introduced here and the associated ionospheric effects will be validated against and compared with the traditional scheme of the calculations based on the expansions of the phase advance in terms of powers of the inverse frequencies. In the next section, this will be discussed in more detail.

5 Traditional technique

For calculations according to the traditional technique, the representation was employed as developed in the paper by Gherm et al. (2006). According to this paper, the phase advance in the case when the isotropic trajectories are utilized when performing calculations is represented as follows:

$$\begin{aligned} \psi \left( {\mathbf{r}\left( L \right) } \right)= & {} L-\frac{1}{2}\mathop {\int }\limits _0^L {X\left( {\mathbf{r}\left( z \right) } \right) } {\hbox {d}}z-\frac{1}{2}\mathop {\int }\limits _0^L {X\left( {\mathbf{r}\left( z \right) } \right) } Y_l \left( {\mathbf{r}\left( z \right) } \right) {\hbox {d}}z\nonumber \\&-\frac{1}{2}\mathop {\int }\limits _0^L {\mathbf{l}_1^2 \left( z \right) } {\hbox {d}}z-\frac{1}{8}\mathop {\int }\limits _0^L {X^{2}\left( {\mathbf{r}\left( z \right) } \right) } {\hbox {d}}z. \end{aligned}$$
(31)

In (31), the integration is carried out along straight line-of-sight paths \(\mathbf{r}\left( z \right) \), z being the distance variable measured along the ray, and L is the true geometrical distance (true distance) between the receiver and the satellite. In the fourth term of the equation,

$$\begin{aligned} \mathbf{l}_1 \left( z \right) =\mathbf{l}_1^0 -\frac{1}{2}\mathop {\int }\limits _0^z {\nabla _\bot X\left( {\mathbf{r}\left( {z^{\prime }} \right) } \right) {\hbox {d}}z^{\prime }}. \end{aligned}$$
(32)

In (32), \(\mathbf{l}_1^0 \) is the constant, and the operator \(\nabla _\bot \) produces the component of the gradient orthogonal to the straight line of sight between the communicating points. The constant \(\mathbf{l}_1^0 \) is chosen to solve the homing-in problem through the relationship

$$\begin{aligned} \mathbf{l}_1^0 = \frac{1}{2L}\mathop {\int }\limits _0^L {{\hbox {d}}z} \mathop {\int }\limits _0^z {\nabla _\bot X\left( {\mathbf{r}\left( {z^{\prime }} \right) } \right) {\hbox {d}}z^{\prime }} . \end{aligned}$$
(33)

In (32) and (33), the terms containing the geomagnetic field have been omitted as compared to the corresponding equations in Gherm et al. (2006), so that equation (31) presents the ionospheric effects calculated for the isotropic trajectories, governed by the ray path equations (6), but for the anisotropic dielectric permittivity (1). As was already mentioned above, our estimates show that employing the isotropic ray path equations results in a negligibly small error for the phase advance of the order of \(10^{-12}\) m.

In equation (31), the pure distance excess due to the curved path and another term proportional to \(\left( {\nabla _\bot X} \right) ^{2}\) along the straight line of sight are rigorously summed up in explicit form. It can be shown analytically that the first of these terms is also proportional to \(\left( {\nabla _\bot X} \right) ^{2}\) that they have opposite signs, one to the other, and one is the half of the other in absolute value.

In the following treatment, the numerical results obtained for the model of the medium of propagation (chosen below) utilizing the alternative technique presented here are compared to the results of calculations according to the traditional technique outlined in this section. Before this, we note that for frequencies of 1 GHz and higher, the traditional technique has been validated against the results of the direct ray tracing by many authors, including ourselves (e.g., Strangeways and Ioannides 2002; Gherm et al. 2006; Hoque and Jakowski 2008; Kashcheyev et al. 2012). This gives validity to its use in validating the results of calculations employing the alternative technique developed here.

6 Numerical results for the phase advance

The main goal of the numerical calculations is to (i) present the quantitative results obtained employing the newly proposed technique, (ii) show its advantages, (iii) determine how it corresponds to the traditional treatment in terms of the series in the inverse powers of the transmission frequency, and (iv) determine for what conditions/parameters it works better than the traditional treatment.

6.1 Ionospheric model for calculations

To perform numerical calculations according to the new analytical technique described above, any model of the ionosphere can be utilized which provides the vertical profile of the electron density of the ionosphere and the horizontal (angle) gradients of the electron density above the point of observation, expressed in the spherical coordinates introduced above. For any particular situation where there is no direct experimental measurement of the profile, any ionospheric model which provides electron density profiles (e.g., IRI (Bilitza et al. 2014) or NeQuick (Nava et al. 2008)) could be utilized. This method enables the adequate modeling of the real horizontal gradients by only defining them above the observation point and in their having the same dependence on angle variables when integrating along the real curved paths of propagation corresponding to the spherically symmetric ionosphere equations (24–26). Obviously, the vertical gradient of the profile, which is explicitly integrated in (24–26), is also available once the vertical ionospheric profile is specified.

The calculations according to both the techniques developed here and the traditional treatment according to equation (31) were carried out for the permittivity of the ionosphere modeled by the function:

$$\begin{aligned} \varepsilon =1-X_{\max } F\left( \zeta \right) f\left( {\vartheta ,\varphi } \right) , \end{aligned}$$
(34)

where the vertical profile of the electron density is represented by the Chapman layer:

$$\begin{aligned} F\left( \zeta \right) =\exp \left\{ {0.5\left[ {1-\zeta -\exp \left( {-\zeta } \right) } \right] } \right\} \end{aligned}$$
(35)

with \(\zeta =\frac{r-h_m -R_e }{H}\), \(h_m \) is the height of the maximum of the electron density, \(R_e \) is the radius of the Earth, H is the scale height of the layer; \(X_{\max } =\frac{\omega _{pl\max }^2 }{\omega ^{2}}\) and \(\omega _{pl\max } \) is the maximum plasma frequency in the layer. In the calculations, the following values of the parameters of Chapman layer were utilized: \(h_m = 300\) km, \(R_e = 6400\) km, \(H = 60\) km and \(\omega _{pl\max } = 2\pi \cdot 10\) MHz. For this layer, the vertical TEC is 30.76 TEC units.

The angle function \(f\left( {\vartheta ,\varphi } \right) \) in equation (28) specifies the dependence of the maximum plasma frequency on the horizontal (angle) variables. Some typical values of the angle gradients, given by IRI/NeQuick, were chosen and utilized in calculations according to equations (23–26). Actually, these can be any values of the gradients up to the highest values actually observed in the ionosphere. In the following treatment, the normalized angular– variable derivatives of the function \(f\left( {\vartheta ,\varphi } \right) \), as shown in equations (36), are determined as:

$$\begin{aligned} a_\vartheta =\frac{1}{f\left( {\vartheta ,\varphi } \right) }\frac{df\left( {\vartheta ,\varphi } \right) }{{\hbox {d}}\vartheta } \hbox { and } a_\varphi =\frac{1}{f\left( {\vartheta ,\varphi } \right) }\frac{df\left( {\vartheta ,\varphi } \right) }{{\hbox {d}}\varphi } ,\nonumber \\ \end{aligned}$$
(36)

As has already been shown above, the contribution into the full phase advance of the derivative in the variable \(\varphi \) is significantly smaller than the contribution of the derivative in the variable \(\vartheta \), and, additionally, is, in effect, negligibly small as will be shown below. In calculations of the main contribution due to the first \(\vartheta \)- derivative, the value of \(a_\vartheta \) in equation (36) varies in the range from \(-0.01\) to \(-0.1\), for the IRI electron density model as shown in Fig. 1.

Then, considering the first of the relationships in equations (36), its solution is in the form

$$\begin{aligned} f\left( \vartheta \right) =e^{a_\vartheta \vartheta } \end{aligned}$$
(37)

It is taken in this treatment that, above the receiver, it is always \(f\left( 0 \right) =1\). In the spherical coordinate system introduced above in which all the equations were derived, the receiver is placed on the Earth’s surface at the point \( (R_e ,0,0)\), and the transmitter has the coordinates \( (R_S ,\vartheta _s ,0)\).

In the next subsection, when performing numerical calculations according to the technique introduced above, the case will be considered where the spherically symmetric ionosphere, producing the zero-order approximation for the phase advance, will be specified as at the pierce point for each path of propagation (equations (29, 30)). However, relationships (24, 26) and (25, 27) are also of use if some particular effects of the ionosphere just above a ground based receiver, or below a satellite, are of a particular interest.

The results will be presented below as functions of the transmission frequency \(f (\omega =2\pi f)\) for the limiting cases of \(f= 1575\) and 150 MHz and the angular separation \(\vartheta _s \) between the points of transmission and reception for any reasonable given value of the horizontal gradients of the ionospheric permittivity (electron density). The angular separation varied from \(0^{\circ }\) to \(72^{\circ }\), which corresponds to the zenith angle changing from \(0^{\circ }\) (vertical propagation) to about \(90^{\circ }\)(almost horizontal propagation). The satellite transmission point was taken to be at 20,000 km above the Earth’s surface.

Table 1 Ionospheric effect for the spherically symmetric ionosphere, calculated employing the new technique (columns 2 and 3) and the traditional technique (columns 4 and 5)
Full size table

As mentioned above, for extracting physically reasonable values of the horizontal gradients, the IRI model on January 27, 2003, at 13.30 LT of the ionosphere near the height of the maximum of the electron density, presented in Fig. 1, was utilized. A wide range of the values of horizontal gradients of the electron density are present here starting from very small up to the maximum corresponding to the equatorial anomaly crest.

6.2 Validation of new technique

First of all, the general version of the method presented here, given by equations (23, 29, 30), will be validated against the traditional technique of calculating the ionospheric effects for the model ionosphere as it is outlined in Sect. 5. For the model of the ionosphere previously described, calculations were performed employing both the newly developed and traditional techniques for the conditions of very strong horizontal gradients as in the wall of the equatorial anomaly shown in Fig. 1. This is the worst case of propagation, and the value \(a_\vartheta =-0.1\) in the model of the ionosphere introduced above corresponds to this case.

First, the comparison was performed for the spherically symmetric case, when the new technique provides the rigorous solution. Although similar comparisons for frequencies of the order of 1 GHz have been made by a number of authors, here the specific aim is to understand how effective the new technique is in the explicit summing up of the series of the inverse frequency powers in the traditional treatment. These results are presented in Table 1.

As shown in Table 1, in the high-frequency case (1575 MHz), the results obtained by the two techniques are practically identical (the difference is of the order of 0.01 mm). This implies that the traditional technique is quite adequate for such high frequencies, as it produces practically the same results as given by the rigorous solution. On the contrary, in the low-frequency case (150 MHz), the difference becomes notable (order of 20 cm) and this difference is due to the rigorous summing up all the terms in the inverse powers provided by the alternative technique introduced here.

When the horizontal gradients of the electron density of the ionosphere are also taken into account according to the relationships presented above, to obtain the best results, it is of importance to properly choose the location where the zero-order spherically symmetric electron density profile and the horizontal gradients are specified. The logical choice would appear to be to specify the vertical electron density distribution and the horizontal electron density gradient at the pierce points chosen individually for each slant ray path. Below we adopt this combination comparing these results to those obtained for the same conditions of propagation utilizing the traditional technique of calculation.

In Table 2, results are presented for the ionospheric effect \((\psi _{0p} +\psi _{1p} -L),\) obtained employing equations (29, 30) for the general case, when the effect of the horizontal gradients of the ionosphere is also taken into account. Comparison is made with the results of calculations for the same ionospheres calculated by the traditional technique \((\psi _\mathrm{trad} -L)\). Table 2 presents the results for a small value of the horizontal gradient (\(a_\vartheta = -0.01\)), whereas Table 2 gives the corresponding results for the case of a large gradient (\(a_\vartheta = -0.1\)). For the small gradient case, the data show a discrepancy in the full phase advance between the new and traditional treatments of about 4 cm for very slant propagation at the higher frequency of 1575 MHz and about 3 m at the lower frequency of 150 MHz. For an extremely high value of the horizontal gradient (\(a_\vartheta = -0.1\)), these discrepancies were found to be correspondingly 30 cm and 30 m. Additionally, it should be pointed out that the angle dependence of the phase full advance is monotonic for small gradients of the electron density but is not necessarily monotonic for the other case of the large horizontal gradients.

Table 2 Ionospheric effect taking account of horizontal gradients of the ionosphere, calculated employing the new technique (columns 2 and 3) and the traditional technique (columns 4 and 5) in the conditions of (a) a small horizontal gradient (\(\alpha _{\vartheta }=-\)0.01) and (b) a large horizontal gradient (\(\alpha _{\vartheta }=-\)0.1). Here L is the full phase advance for free space propagation (true distance)
Full size table

According to the values presented in Table 2, the discrepancy between the results for the ionospheric effect obtained employing the two techniques (traditional and alternative, based on the vertical electron density profile and the horizontal gradients given at the appropriate pierce point) is reasonably small in the case of small horizontal gradients. However, when the horizontal gradients are rather large, the discrepancy in the results increases to unacceptably large values, even in the case of the higher transmission frequency of 1575 MHz. In the following subsection, it will be shown how this significantly large error can be reduced.

6.3 “Effective” spherically symmetric ionosphere

To reduce this relatively high discrepancy shown above to practically negligible values when utilizing the new and traditional approaches even in the case of large horizontal gradients, the models for the zero-order spherically symmetric ionosphere and horizontal gradients should be altered in a specific way. As was found, the best fit between the results of calculating the full ionospheric effect for the given model of the ionosphere adopted here, employing the traditional and the alternative techniques, can be achieved by introducing the “effective” spherically symmetric ionosphere according to the following relationship for the dielectric permittivity

$$\begin{aligned} \varepsilon _{eff} (r) =\varepsilon \left( {r,\vartheta _{00} (r),0} \right) . \end{aligned}$$
(38)

Here the function \(\vartheta _{00} (r)\) denotes the straight line between the given start and end points of transmission. The profile given by equation (38) can be understood as the real slant profile of the electron density corresponding to a given oblique path of propagation being projected to the vertical at the pierce point of the slant path by concentric spheres centered at the origin of the spherical coordinate system. Such an “effective” spherically symmetric ionosphere actually takes account of the major part of the horizontal gradient of the real ionosphere.

Table 3 Ionospheric effect calculated employing the “effective” spherically symmetric model of the electron density of the ionosphere, the new technique (columns 2 and 3) and the traditional technique (columns 4 and 5) in the conditions of strong horizontal gradients (\(a_\vartheta = -0.1\))
Full size table

Then, for profile (38) the field phase advance is given by the following integral:

$$\begin{aligned} \psi _{eff} \left( \mathbf{r} \right) =\mathop {\int }\limits _{R_e }^{R_s } {\sqrt{\varepsilon \left( {r,\vartheta _{00} (r),0} \right) }\sqrt{1+h_\vartheta ^{2}\left( {\frac{{\hbox {d}}\vartheta _0 (r)}{{\hbox {d}}r}} \right) ^{2}}{\hbox {d}}r} . \end{aligned}$$
(39)

In Table 3, the results of calculation of the ionospheric effect\((\psi _{eff} -L)\), utilizing this model, and those obtained with the traditional technique \((\psi _\mathrm{trad} -L)\) for the same model of the ionosphere, are both presented. They demonstrate an extremely high congruence. It should be additionally noted here that, when performing calculations according to (39), both the first-order approximation \(\psi _1 \left( \mathbf{r} \right) \) and also the second-order approximation \(\psi _2 \left( \mathbf{r} \right) \) shown in equation (23) appear to be negligibly small, being of the order of the error of calculation of the zero-order approximation for the worst case of the large horizontal gradients.

This means that a very simple formula (39), which solely contains the introduced “effective” spherically symmetric ionosphere, permits the comprehensive solution of the propagation problem under consideration. In turn, the above conclusion also implies that, although the real paths of propagation between a satellite and receiver are in fact in three dimensions, the contribution of the ray bending out of the great circle plane \(\left( {r,\vartheta , 0} \right) \) does not contribute any significant addition into the full effect of the phase advance. In the following treatment, the solution constructed according to equation (38), containing the introduced “effective” spherically symmetric ionosphere, will be used as the reference solution when comparison is made to other results.

6.4 Phase advances of magneto-ionic components

When investigating the effects due to the Earth’s magnetic field, equations (14, 22) yield:

(40)

So far, simply to indicate how the geomagnetic field is implemented in the alternative technique presented here, according to (40), we confined our consideration to the simplest case of a magnetic field constant along the path of propagation, which had the magnitude and the direction given by that at the pierce point of the given path of propagation, as in Bassiri and Hajj (1993). These quantities were taken from the model IGRF11, available in Finlay (2010). In the more recent paper by Hoque and Jakowski (2008), the more advanced description of the effect of the Earth’s magnetic field is presented and the comparison with a simpler model as above is given.

Table 4 Effect of the Earth’s magnetic field: the ionospheric phase advance calculated utilizing the effective ionospheric model introduced by equation (39)
Full size table

The following details of the calculations are similar to the isotropic case with the only distinction that the parameter \(X_{\max } =\frac{\omega _{pl\max }^2 }{\omega ^{2}}\) is replaced by

$$\begin{aligned} X_{\max }= & {} \frac{\omega _{pl\max }^2 }{\omega ^{2}}\nonumber \\&\times \left( {1\pm \frac{\omega _g \left( {R_{\max } ,\vartheta _{pp} ,0} \right) }{\omega }\cos \chi \left( {R_{\max } ,\vartheta _{pp} ,0} \right) } \right) .\nonumber \\ \end{aligned}$$
(41)

Here \(R_{\max } \) is the radius (in the introduced spherical coordinates) where the ionospheric electron density has its maximum. In the case of the right-hand circular polarization, the sign “plus” should be used.

In calculations of the additional effect due to the Earth’s magnetic field for this polarization, the IGRF model of the magnetic field was utilized, which provides the value and direction of the geomagnetic field for any date and geographical location. Additionally it was assumed that the geomagnetic field was constant along the propagation path through the ionosphere and given by its value at the pierce point.

The calculations were performed for the geometry where the local spherical coordinate system is chosen in the form that its polar axis is given by the Earth’s origin and the receiver placed at the point with coordinates (\(20^{\circ }\)N, \(115^{\circ }\)E). Propagation from a satellite to the south was considered, so that the elevation angles of a satellite lie in the plane defined by the Earth’s center, the North Pole and the receiver. The distribution of the geomagnetic field is taken for the date of July 14, 2014. According to Fig. 1, for the chosen location, the typical value of a fairly strong horizontal gradient of the electron density is \(a_\vartheta =-0.1\).

The calculated effects of the magnetic field are presented in Table 4. In the left column, the full ionospheric effect for different elevation angles of a satellite is given for the isotropic case as the difference between the full phase advance and that for propagating the true line-of-sight distance at velocity c. In the right column, the same difference is presented taking account of the geomagnetic field.

The numerical results shown in Table 4 demonstrate that, at higher frequency (1575 MHz), the effect of the geomagnetic field is of an order of mm even for very oblique propagation, whereas, for the lower-frequency (150 MHz) case, it may reach the value of about 2 m.

7 Conclusion

An alternative approach to the traditionally employed methods for treating the ionospheric range errors in the GNSS positioning has been developed and presented. It permits explicitly accounting for the effects due to the horizontal gradients of the electron density of the ionosphere. By contrast with many traditional treatments, where the expansion of the solution for the phase advance is represented as the series in the inverse frequency powers and the main term of the expansion corresponds to the true line-of-sight distance from the transmitter to the receiver, in the alternative technique the zero-order term is the rigorous solution for a spherically layered ionosphere with any given vertical electron density profile. The first-order term in the solution explicitly represents the effects due to the horizontal gradients of the electron density of the ionosphere, and the second-order term appears to be negligibly small once the spherically symmetric ionosphere is properly chosen for the zero-order approximation in the phase advance.

It has been shown that, for the higher L-band transmission frequencies, such as 1575 MHz (GPS L1), the technique presented provides results for the phase advance calculations which are in good agreement with those utilizing the traditional approach (when summing up the contributions of the different-order terms in the inverse powers of the transmission frequency) for the same conditions of propagation. However, when the transmission frequency reduces to 150 MHz or lower, the discrepancy increases. This is because the new technique presented here provides a much more accurate solution, and it is arranged in the way that its zero-order approximation rigorously and explicitly already sums up all the terms of the inverse frequency powers.

It has been also shown that it is possible to introduce and utilize the specially constructed “effective” spherically symmetric effective ionosphere (which can take account of the major contribution of the horizontal gradients of the ionospheric electron density), permitting an even more accurate solution for the ionospheric contribution in the field phase and solely employing the zero-order approximation for the phase advance given by the main term in (23). This is, in particular, of special importance for obtaining fast and accurate estimates of the ionospheric effect for single-frequency ionosphere correction methods.