Estimation for partially varying-coefficient single-index models with distorted measurement errors

Abstract

In this paper, we study partially varying-coefficient single-index model where both the response and predictors are observed with multiplicative distortions which depend on a commonly observable confounding variable. Due to the existence of measurement errors, the existing methods cannot be directly applied, so we recommend using the nonparametric regression to estimate the distortion functions and obtain the calibrated variables accordingly. With these corrected variables, the initial estimators of unknown coefficient and link functions are estimated by assuming that the parameter vector $\beta$ is known. Furthermore, we can obtain the least square estimators of unknown parameters. Moreover, we establish the asymptotic properties of the proposed estimators. Simulation studies and real data analysis are given to illustrate the advantage of our proposed method.

Appendix: Proof of the main results

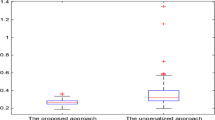
We first impose some regularity conditions for the proofs of the theorems (Fig. 4).

Fig. 4

The application to Boston housing data. a Baseline function; b–e the coefficient functions for CRIM, RM, TAX and NOX; f the estimator of function $\alpha (\cdot )$

C1. :

For any $\beta$ near $\beta _0$, the desity funtion r(t) of $\beta ^TX$ is Lipschitz continuous and bounded away from 0 on the support $\mathcal {T}_{\beta }=\left\{ \beta ^Tx: x \in \mathcal {X} \right\}$, where the set $\mathcal {X}$ is an open convex set.

C2. :

The functions $\alpha (t)$ has bounded and continuous derivatives up to order 2 on $\mathcal {T}_{\beta _0}$.

C3. :

For $l=1,.., p$ and $r=1,..., q$, the functions $\mu _{1l}(t)$ and $\mu _{2r}(t)$ have bounded and continuous derivatives up to order 2 on $\mathcal {T}_{\beta _0}$, where $\mu _{1l}(t)$ is the lth of $\mu _1(t)=E(X|\beta ^TX=t)$ and $\mu _{2r}(t)$ is the rth of $\mu _2(t)=E(Z|\beta ^TX=t)$.

C4. :

The density function of U, f(u), is continuous in $\mathcal {N}(u_0)$ and $\theta _j(\cdot )$ has continuous derivatives of order 2 in $\mathcal {N}(u_0)$, where $\mathcal {N}(u_0)$ denotes some neighbourhood of $u_0$ and $f(u_0)>0$.

C5. :

The joint function of ($\beta ^TX, U)$, f(t, u), is bounded away from 0 on the support $\mathcal {T}_{\beta _0}\times \mathcal {N}(u_0)$. And the functions $f(t, u), \varkappa _1(t, u)$ and $\varkappa _{2j}(t, u)$ have bounded partial derivatives up to order 4, where $\varkappa _{2j}(t, u)$ is the jth of $\varkappa _2(t, u)$, for $j=1,...,q$.

C6. :

For $s>2$, $l=1,..., p$ and $r=1,...,q$, E[Y], $E[X_l]$ and $E[Z_r]$ are bounded away from 0 and $E[Y^2]$, $E[X^2_l]$, $E[Z^2_r]$, $E\left( |Z_{1r}|^{2s}\mid U=u\right)$, $E\left( |\varepsilon |^{2s}\mid U=u\right)$, $E(|Z_{1r}|^{s}\mid \beta ^TX=t, U=u)$ and $E(|\varepsilon |^{s}\mid X=x, Z=z, U=u)$ are bounded.

C7. :

Suppose p(v) is the density function of V. For $r \in R^{q}$ and $l \in R^{p}$, $g_{Y}(v)=\psi (v)p(v)$, $g_{r}(v)=\phi _r(v)p(v)$ and $g_{l}(v)=\varphi _l(v)p(v)$ are greater than a positive constant and are differential. For some neighbourhood of origin, which denotes as $\Delta$, and some constant $c>0$, for any $\delta \in \Delta$, we have

$$\begin{aligned} \begin{aligned}&\left| g_{Y}^{(3)}(u+\delta )-g_{Y}^{(3)}(u)\right| \le c|\delta |,\\&\left| g_{r}^{(3)}(u+\delta )-g_{r}^{(3)}(u)\right| \le c|\delta |, \quad 1 \le r \le q ,\\&\left| g_{l}^{(3)}(u+\delta )-g_{l}^{(3)}(u)\right| \le c|\delta |, \quad 1 \le l \le p ,\\&\left| p^{(3)}(u+\delta )-p^{(3)}(u)\right| \le c|\delta |. \end{aligned} \end{aligned}$$

C8. :

As $n\rightarrow \infty$, the bandwidth h satisfies:

(1):

$h_1$ is in the range from $O(n^{-1/4}\log n)$ to $O(n^{-1/8})$;

(2):

For some $\varsigma <2-\iota ^{-1}$, where $\iota >2$, $n^{2\varsigma -1}h_{\iota }\rightarrow \infty$ when $\iota =3,4$.

C9. :

The kernel functions $K(\cdot )$ and $K_1(\cdot , \cdot )$ have following properties:

(1):

$K(\cdot )$ is a bounded symmertrical density function on its support $[-1, 1]$ and satisfies the Lipschitz condition;

(2):

$K(\cdot , \cdot )$ is a right continuous kernel function of order 4 with bounded variation and has support $\left[ -1, 1\right] ^2$;

(3):

$\int _{-1}^{1}K(v) d v=1$, $\int _{-1}^{1}vK(v)dv=0$, $\int _{-1}^{1}v^2K(v)dv\ne 0$ and $\int _{-1}^{1}|v|^{i}K(v) d v<\infty$ for $i=1, 2, 3$.

C10. :

The matrices $\Gamma$ and $\Omega (u)$ are positive define, where these matrices are defined in Theorem 2. The components of $\sigma ^2(u)$ and $\Omega (u)$ are continuous at point $u_0$ and $\sigma ^2(u_0)\ne 0$.

Lemma 1

Let $\eta (X)$ be a continuous function satisfying $E[\eta (X)]<\infty$. Suppose that conditions C7-C9 hold, we have

$$\begin{aligned} \sum _{i=1}^{n}(\hat{Y}_{i}-Y_{i}) \eta \left( X_{i}\right)= & {} \frac{1}{2} \sum _{i=1}^{n}\left( Y_{i}-E[Y]\right) \frac{E[Y \eta (X)]}{E[Y]}\\&+\sum _{i=1}^{n}(\tilde{Y}_{i}-Y_{i}) \frac{E[Y \eta (X)]}{E[Y]}+o_{P}(\sqrt{n}). \end{aligned}$$

Proof

This follows a direct result of Cui et al. (2009). $\square$

Lemma 2

Let $(X_1, Y_1),..., (X_n, Y_n)$ be i.i.d bivariate random vectors with joint density function f(x, y). Assume that $K(\cdot )$ is a bounded positive function with bounded support and is Lipschitz continuous. if $E|Y|^s<+\infty$ and $\sup \limits _{x}\int {|y|^sf(x, y)dy}<\infty$, then

$$\begin{aligned} \sup _{x \in D}\left| \frac{1}{n} \sum _{i=1}^{n}\left[ K_{h}\left( X_{i}-x\right) Y_{i}-E\left\{ K_{h}\left( X_{i}-x\right) Y_{i}\right\} \right] \right| =O_{P}\left( \left\{ \frac{\log (1 / h)}{n h}\right\} ^{1 / 2}\right) , \end{aligned}$$

provided that $0<h\rightarrow 0$ and $n^{2\epsilon -1}h\rightarrow \infty$ for some $\epsilon <1-s^{-1}$, where h is a bandwidth and D is some closed set.

Proof

This follows a direct result of Mack and Silverman (1982). $\square$

Proof of Theorem 1

From (2.9), we have

$$\begin{aligned} R_n(u;\beta _0)=\tilde{\hat{\aleph }}(u; \beta _0)^T\omega (u; \beta _0)\tilde{\hat{\aleph }}(u; \beta _0)=\left( \begin{array}{ll} {R_{n, 0}\left( u ; \beta _{0}\right) } &{} {R_{n, 1}\left( u ; \beta _{0}\right) } \\ {R_{n, 1}\left( u ; \beta _{0}\right) } &{} {R_{n, 2}\left( u ; \beta _{0}\right) }, \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \mathcal {A}_n(u; \beta _0)=\tilde{\hat{\aleph }}(u; \beta _0)\omega (u; \beta _0)\tilde{\hat{Y}}=\left( \begin{array}{l} {\mathcal {A}_{n, 0}\left( u ; \beta _{0}\right) } \\ {\mathcal {A}_{n, 1}\left( u ; \beta _{0}\right) } \end{array}\right) . \end{aligned}$$

It can be shown that, for any $\beta \in \mathcal {B}_n$ and each $j=0, 1, 2, 3$,

$$\begin{aligned} R_{n, j}(u_0; \beta )=f(u_0)\Omega (u_0)\mu _j+o_{P}(1), \end{aligned}$$

(A.1)

where $\mu _j=\int u^jK(u)du$. By simple calculation, we have

$$\begin{aligned} R_{n, j}(u_0; \beta )=&\frac{1}{n}\sum _{i=1}^{n}[\hat{Z}_i-\hat{\varkappa }_2(\beta ^T\hat{X}_i, U_i; \beta )]^{\otimes 2}\left( \frac{U_i-u_0}{h_3}\right) ^{j}K_{h_3}\left( U_i-u_0\right) \nonumber \\ =&\frac{1}{n}\sum \limits _{i=1}^n(\hat{Z}_i-Z_i)^{\otimes 2}\left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}\left( U_i-u_0\right) \nonumber \\&+\frac{2}{n}\sum \limits _{i{=}1}^n(\hat{Z}_i-Z_i)\left[ Z_i{-}\varkappa _2(\beta _0^T\hat{X}_i, U_i)\right] ^T\left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}\left( U_i-u_0\right) \nonumber \\&+\frac{1}{n}\sum \limits _{i=1}^n\left[ Z_i-\varkappa _2(\beta _0^T\hat{X}_i, U_i)\right] ^{\otimes 2}\left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}\left( U_i-u_0\right) \nonumber \\&+\!\frac{2}{n}\!\sum \limits _{i=1}^{n}\!\left[ \!\hat{Z}_i\!\!-\!\!\varkappa _2(\beta _0^T\hat{X}_i,\! U_i)\!\right] \!\!\left[ \!\varkappa _2(\beta _0^T\hat{X}_i,\!U_i)\!\!-\!\!\hat{\varkappa }_2(\beta ^T\hat{X}_i,\!U_i; \beta )\!\right] ^T\!\!\!\nonumber \\&\times \!\!\left( \!\frac{U_i\!-\!u_0}{h_3}\!\right) ^j\!\!\!K_{h_3}\!\left( U_i\!-\!u_0\right) \nonumber \\&+\frac{1}{n}\sum _{i=1}^{n}\left[ \varkappa _2\left( \beta _0^T\hat{X}_i, U_i\right) -\hat{\varkappa }_2\left( \beta ^T\hat{X}_i, U_i; \beta \right) \right] ^{\otimes 2}\nonumber \\&\left( \frac{U_i-u_0}{h_3}\right) ^{j}K_{h_3}\left( U_i-u_0\right) \nonumber \\&\equiv R_1(u_0; \beta )+R_2(u_0; \beta )+R_3(u_0; \beta )+R_4(u_0; \beta )+R_5(u_0; \beta ). \end{aligned}$$

(A.2)

Using the arguments proposed in Zhu and Fang (1996), we have

$$\begin{aligned} \begin{aligned} \sup _{u}|\hat{p}(u)-p(u)|&=O\left( h^{4}+n^{-1 / 2} h^{-1} \log n\right) ,\quad a.s., \\ \sup _{u}\left| \hat{g}_{Y}(u)-g_{Y}(u)\right|&=O_{P}\left( h^{4}+n^{-1 / 2} h^{-1} \log n\right) , \end{aligned} \end{aligned}$$

(A.3)

where p(u) and $g_Y(u)$ are defined in condition C7. Then, under the condition C6 and using Lamma 2, we have

$$\begin{aligned} \begin{aligned} R_1(u_0; \beta )&=\left[ f(u_0)\mu _jE(ZZ^T\mid U=u_0)+o_{P}(1)\right] \cdot O_{P}\left( {C_n}^2\right) =o_{P}(n^{-1/2}), \end{aligned} \end{aligned}$$

(A.4)

where $C_n=h_1^4+n^{-1/2}h_1^{-1}\log n$. By decomposing $R_2(u_0; \beta )$, we have

$$\begin{aligned} R_2(u_0; \beta )&=\frac{2}{n}\sum \limits _{i=1}^{n}(\hat{Z}_i-Z_i)\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] ^T\left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}\left( U_i-u_0\right) \nonumber \\&\quad +\frac{2}{n}\sum \limits _{i=1}^{n}(\hat{Z}_i-Z_i)\left[ \varkappa _2\left( \beta _0^TX_i, U_i\right) -\varkappa _2\left( \beta _0^T\hat{X}_i, U_i\right) \right] ^T\nonumber \\&\quad \times \left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}(U_i-u_0)\nonumber \\&\equiv R_{21}(u_0; \beta )-R_{22}(u_0; \beta ). \end{aligned}$$

(A.5)

According to (A.3) and (A.4), $R_{21}(u_0; \beta _0)=o_{P}(1)$ can be easily proved. By using Taylor’s expansion for $\varkappa _2\left( \beta _0^T\hat{X}_i, U_i\right)$ at $\hat{X}_i$, we can obtain

$$\begin{aligned} \frac{1}{2}R_{22}(u_0; \beta )&=f(u_0)\mu _jE\left[ \left( \hat{Z}-Z\right) \sum _{l=1}^{p}\frac{\partial \varkappa _2\left( \beta _0^TX^{*}, U\right) }{\partial x_l}\left( \hat{X}_l-X_l\right) \mid U=u_0\right] \nonumber \\&\quad -\frac{1}{2}f(u_0)\mu _jE\left[ (\hat{Z}-Z)\sum _{l=1}^{p}\sum _{r=1}^{p}\frac{\partial ^2\varkappa _2(\beta _0^TX^{*}, U)}{\partial x_l\partial x_r}\right. \nonumber \\&\left. \quad (\hat{X}_{l}-X_{l})(\hat{X}_{r}-X_{r})\mid U=u_0\right] \nonumber \\&\quad +o_{P}(1)\nonumber \\&=c_1f(u_0)\mu _j n^{-1} O_{P}\left( n{C_n}^2\right) +c_1f(u_0)\mu _j n^{-1} O_{P}\left( n{C_n}^3\right) +o_{P}(1)\nonumber \\&=o_{P}(1), \end{aligned}$$

(A.6)

where $X^{*}_i=(X_{i1}^{*},..., X_{ip}^{*})$ with $X^{*}_{il}$ is point between $\hat{X}_{il}$ and $X_{il}$. Together with (A.5), we have $R_2(u_0; \beta )=o_{P}(1)$. Under the assumption (2) , we can show that

$$\begin{aligned} \varkappa _{2r}(\beta ^TX_i, U_i)=E\left( \hat{Z}_r\mid \beta ^TX_i, U_i\right) =E\left( Z_r\mid \beta ^TX_i, U_i\right) , \end{aligned}$$

for $r=1,..., q$. Thus, by the same argument as that for (A.8), we have

$$\begin{aligned} R_3(u_0; \beta )=f(u_0)\Omega (u_0)\mu _j+o_{P}(1). \end{aligned}$$

(A.7)

Applying the Theorem 2 of Einmahl and Mason (2005), we show that

$$\begin{aligned} \sup _{(x, \beta ) \in \mathcal {X} \times \mathcal {B}_{n}, u \in \mathcal {N}\left( u_{0}\right) }\left\| \hat{\varkappa }_{v}\left( x^{\mathrm {T}} \beta , u ; \beta \right) -\varkappa _{v}\left( x^{\mathrm {T}} \beta _{0}, u\right) \right\| =O\left( \left[ \frac{\log n}{n h_{2}}\right] ^{1 / 2}+h_{2}^{2}\right) , \end{aligned}$$

(A.8)

for $v=1, 2$, in probability 1, where $\mathcal {X}$ and $\mathcal {B}_n$ are defined in Sect. 2 and $\mathcal {N}(u_0)$ is defined in condition C4. Therefore, by direct calculation, it can be prove that $R_4(u_0; \beta )=o_{P}(1)$ and $R_5(u_0; \beta )=o_{P}(1)$. Together with (A.4)–(A.7), we can acquire (A.2). It is followed immediately that

$$\begin{aligned} R_n(u_0; \beta )=R(u_0)+o_{P}(1), \end{aligned}$$

for any $\beta \in \mathcal {B}_n$, where $R(u_0)=f(u_0)\Omega (u_0)\otimes diag(1, \mu _2)$ with $\otimes$ be the Kronecker product.

To prove the asymptotic normality of $\check{\theta }(u_0; \beta )$, we define a center vector of $\mathcal {A}_n(u_0; \beta )$ as

$$\begin{aligned} \mathcal {A}^{*}_{n,j}(u_0; \beta )=\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i\left( \frac{U_i-u_0}{h_3}\right) ^jK_{h_3}\left( U_i-u_0\right) \left[ \tilde{\hat{Y}}_i-\theta ^T(U_i)\tilde{\hat{Z}}_i\right] , \end{aligned}$$

(A.9)

then, we can obtain

$$\begin{aligned} \mathcal {A}_{n}^{*}\equiv \mathcal {A}_{n}^{*}(u_0; \beta )=\left( \begin{array}{l} {\mathcal {A}_{n, 0}^{*}\left( u_{0} ; \beta \right) } \\ {\mathcal {A}_{n, 1}^{*}\left( u_{0} ; \beta \right) } \end{array}\right) . \end{aligned}$$

For simplicity of expression, we denote that $\mathcal {A}_{n, j}=\mathcal {A}_{n, j}(u_0; \beta )$, $\mathcal {A}_n=\mathcal {A}_n(u_0; \beta )$, $R_n=R(u_0; \beta )$ and $R_{n, j}=R_{n, j}(u_0; \beta )$. Using Taylor’s expansion for $\theta (U_i)$ at $u_0$, we have

$$\begin{aligned} \mathcal {A}_{n, j}-\mathcal {A}_{n, j}^{*}=\theta \left( u_{0}\right) R_{n, j}+h_{3} \theta ^{\prime }\left( u_{0}\right) R_{n, j+1}+\frac{h_{3}^{2}}{2} \theta ^{\prime \prime }\left( u_{0}\right) R_{n, j+2}+o_{P}\left( h_{3}^{2}\right) , \end{aligned}$$

for any $\beta \in \mathcal {B}_n$ and $j=0,1$. Thus, it can be proved that

$$\begin{aligned} \mathcal {A}_{n}-\mathcal {A}_{n}^{*}=R_{n}\left( \begin{array}{c} {\theta \left( u_{0}\right) } \\ {h_{3} \theta ^{\prime }\left( u_{0}\right) } \end{array}\right) +\frac{h_{3}^{2}}{2} \theta ^{\prime \prime }\left( u_{0}\right) \left( \begin{array}{c} {R_{n, 2}} \\ {R_{n, 3}} \end{array}\right) +o_{P}\left( h_{3}^{2}\right) , \end{aligned}$$

for any $\beta \in \mathcal {B}_n$. According to (2.9), we obtain

$$\begin{aligned} \left( \begin{array}{c} {\check{\theta }\left( u_{0} ; \beta \right) -\theta \left( u_{0}\right) } \\ {h_{3}\left[ \check{\theta }^{\prime }\left( u_{0} ; \beta \right) -\theta ^{\prime }\left( u_{0}\right) \right] } \end{array}\right) =R_n^{-1} \mathcal {A}_{n}^{*}+\frac{h_{3}^{2}}{2} \theta ^{\prime \prime }(u_0)\left( \begin{array}{l} {\mu _{2}} \\ {\frac{\mu _{3}}{\mu _{2}}} \end{array}\right) +o_{P}\left( h_{3}^{2}\right) , \end{aligned}$$

for any $\beta \in \mathcal {B}_n$, which implies

$$\begin{aligned} \check{\theta }(u_0; \beta )-\theta (u_0)=f^{-1}(u_0)\Omega ^{-1}(u_0)\mathcal {A}_{n, 0}^{*}(u_0; \beta )+\frac{1}{2}h_3^2\mu _2\theta ^{\prime \prime }(u_0)+o_{P}(h_3^2), \end{aligned}$$

for any $\beta \in \mathcal {B}_n$. Therefore, to get the asymptotic normality of $\check{\theta }(u_0; \beta )$, we only need to prove that

$$\begin{aligned} \sqrt{n h_{3}} \mathcal {A}_{n, 0}^{*}\left( u_{0} ; \beta \right) {\mathop {\longrightarrow }\limits ^{D}} N\left( 0, \nu _{0} f\left( u_{0}\right) \Sigma _{\theta }(u_0)\right) , \end{aligned}$$

for any $\beta \in \mathcal {B}_n$. Mimicking to the proof of (A.1), we have

$$\begin{aligned} \mathcal {A}^{*}_{n, 0}(u_0; \beta )&=\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i\varepsilon _iK_{h_3}(U_i-u_0)+\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i(\hat{Y}_i-Y_i)K_{h_3}(U_i-u_0)\\&\quad +\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i\left[ \varkappa _1(\beta _0^TX_i, U_i)-\hat{\varkappa }_1(\beta ^T\hat{X}_i, U_i; \beta )\right] K_{h_3}(U_i-u_0)\\&\quad -\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i\theta ^T(U_i)(\hat{Z}_i-Z_i)K_{h_3}(U_i-u_0)\\&\quad -\frac{1}{n}\sum _{i=1}^{n}\tilde{\hat{Z}}_i\theta ^T(U_i)\left[ \varkappa _2(\beta _0^TX_i, U_i)-\hat{\varkappa }_2(\beta ^T\hat{X}_i, U_i; \beta )\right] K_{h_3}(U_i-u_0)\\&\equiv J_1(u_0)+J_2(u_0)+J_3(u_0)-J_4(u_0)-J_5(u_0). \end{aligned}$$

$J_1(u_0)$ can be decomposed as

$$\begin{aligned} J_1(u_0)&=\frac{1}{n}\sum _{i=1}^{n}\left( \hat{Z}_i-Z_i\right) \varepsilon _iK_{h_3}\left( U_i-u_0\right) \nonumber \\&\quad +\frac{1}{n}\sum _{i=1}^{n}\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] \varepsilon _iK_{h_3}\left( U_i-u_0\right) \nonumber \\&\quad +\frac{1}{n}\sum _{i=1}^{n}\left[ \varkappa _2\left( \beta _0^TX_i, U_i\right) -\varkappa _2\left( \beta _0^T\hat{X}_i, U_i\right) \right] \varepsilon _iK_{h_3}\left( U_i-u_0\right) \nonumber \\&\quad +\frac{1}{n}\sum _{i=1}^{n}\left[ \varkappa _2\left( \beta _0^T\hat{X}_i, U_i\right) -\hat{\varkappa }_2\left( \beta _0^T\hat{X}_i, U_i; \beta _0\right) \right] \varepsilon _iK_{h_3}\left( U_i-u_0\right) \nonumber \\&\quad +\frac{1}{n}\sum _{i=1}^{n}\left[ \hat{\varkappa }_2\left( \beta _0^T\hat{X}_i, U_i; \beta _0\right) -\hat{\varkappa }_2\left( \beta ^T\hat{X}_i, U_i; \beta \right) \right] \varepsilon _iK_{h_3}\left( U_i-u_0\right) \nonumber \\&\equiv J_{11}(u_0)+J_{12}(u_0)+J_{13}(u_0)+J_{14}(u_0)+J_{15}(u_0). \end{aligned}$$

(A.10)

Combining (A.3) with the assumption of $\varepsilon$ implies that

$$\begin{aligned} n h_3 E\left[ J_{11}(u_0)\right] ^2&\le c_{1} (n h_{3})^{-1} \sum _{i=1}^{n}E\left[ (\hat{Z}_{i}-Z_{i})^T(\hat{Z}_i-Z_i)\right] \nonumber \\&=c_1(nh_3)^{-1}O_{P}\left( nC_n^2\right) \nonumber \\&\rightarrow 0, \end{aligned}$$

(A.11)

where $c_1$ is a constant. Hence, $\sup \limits _{u_0\in \mathcal {N}(u_0)}||J_{11}(u_0)||=o_{P}\left( (nh_3)^{-1/2}\right)$. By the same arguments as that for (A.6) and (A.11), we can prove that $\sup \limits _{u_0\in \mathcal {N}(u_0)}||J_{13}(u_0)||=o_{P}\left( (nh_3)^{-1/2}\right)$. Let $J_{14, j}(\cdot )$, $\varkappa _{2j}(\cdot , \cdot )$ and $\hat{\varkappa }_{2j}(\cdot , \cdot ; \cdot )$ be the jth components of $J_{14}(\cdot )$, $\varkappa _{2}(\cdot , \cdot )$ and $\hat{\varkappa }_{2}(\cdot , \cdot ; \cdot )$ respectively. Based on the Eq. (A.13) in Wang and Xue (2011), we have

$$\begin{aligned} \begin{aligned} E\left[ J_{14, j}\left( u_0\right) \right]&\le \frac{1}{n^2h_3^2}\sum _{i=1}^{n}E\left[ \varkappa _{2j}(\beta _0^T\hat{X}_i, U_i)-\hat{\varkappa }_{2j}(\beta _0^T\hat{X}_i, U_i; \beta _0)\right] ^2\\&=O\left( \left( n^2h_2h_3^2\right) ^{-1}+n^{-1}h_2^4h_3^{-2}\right) . \end{aligned} \end{aligned}$$

Considering the conditions for bandwidths defined in Theorem 1, we get

$$\begin{aligned} J_{14}(u_0)=O_P\left( (nh_3)^{-1/2}\right) . \end{aligned}$$

(A.12)

Note that $||\beta -\beta _0||\le C_1n^{-1/2}$, for $\beta \in \mathcal {B}_n$, where $C_1$ is a constant, we have

$$\begin{aligned} ||J_{15}(u_0)||&\le \sup \limits _{\left( x,\beta \right) \in \mathcal {X}\times \mathcal {B}_n, u\in \mathcal {N}\left( u_0\right) }||\hat{\varkappa }_2^{\prime }\left( \beta ^Tx, u; \beta \right) ||||\beta -\beta _0||\\&\quad \times \frac{1}{nh_3}\sum _{i=1}^{n}|\varepsilon _i|K\left( \frac{U_i-u_0}{h_3}\right) \\&=O_{P}(n^{-1/2}). \end{aligned}$$

This together with (A.10)–(A.12), we have

$$\begin{aligned} J_1(u_0) = J_{12}(u_0)+O_{P}\left( \left( nh_3\right) ^{-1/2}\right) . \end{aligned}$$

uniformly for $\beta \in \mathcal {B}_n$ and $u_0\in \mathcal {N}(u_0)$. Similarly, it can be proved that

$$\begin{aligned} J_{2}(u_0)=\frac{1}{n}\sum _{i=1}^{n}\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] (\hat{Y}_i-Y_i)K_{h_3}\left( U_i-u_0\right) +o_P\left( \left( nh_3\right) ^{-1}\right) , \end{aligned}$$

$J_{3}(u_0)=O_{P}\left( \left( nh_3\right) ^{-1}\right)$, $J_{5}(u_0)=O_{P}\left( \left( nh_3\right) ^{-1}\right)$ and

$$\begin{aligned} J_4(u_0) {=} \frac{1}{n}\sum _{i{=}1}^{n}\left[ Z_i{-}\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] \theta ^T\left( U_i\right) (\hat{Z}_i{-}Z_i)K_{h_3}\left( U_i{-}u_0\right) {+}o_P((nh_3)^{-1}). \end{aligned}$$

Combining above results with (A.11), (A.13) and (A.14), it follows immediately that

$$\begin{aligned} \begin{aligned} \mathcal {A}_{n, 0}^{*}(u_0; \beta )&=\frac{1}{n}\sum _{i=1}^{n}\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] \varepsilon _iK_{h_3}\left( U_i-u_0\right) \\&\quad +\frac{1}{n}\sum _{i=1}^{n}\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] (\hat{Y}_i-Y_i)K_{h_3}\left( U_i-u_0\right) \\&\quad -\frac{1}{n}\sum _{i=1}^{n}\left[ Z_i-\varkappa _2\left( \beta _0^TX_i, U_i\right) \right] \theta ^T\left( U_i\right) (\hat{Z}_i-Z_i)K_{h_3}\left( U_i-u_0\right) \\&\quad +O_{P}\left( \left( nh_3\right) ^{-1}\right) . \end{aligned} \end{aligned}$$

Then, the Lamma 1 and the Slutsky’s Theorem can be used to prove (A.10), and we complete the proof of Theorem 1. $\square$

Proof of Theorem 2

By a direct calculation, we have

$$\begin{aligned} \Xi (\beta )&=(\hat{Y}-\hat{\Theta })(I-\hat{S}_{\beta })\hat{W}^{*}(I-\hat{S}_{\beta })(\hat{Y}-\hat{\Theta })\nonumber \\&+2(\hat{Y}-\hat{\Theta })(I-\hat{S}_{\beta })\hat{W}^{*}(I-\hat{S}_{\beta })(\hat{\Theta }-\check{\Theta })\nonumber \\&+(\hat{\Theta }-\check{\Theta })(I-\hat{S}_{\beta })\hat{W}^{*}(I-\hat{S}_{\beta })(\hat{\Theta }-\check{\Theta })\nonumber \\&\equiv \Xi _1(\beta )-\Xi _2(\beta )+\Xi _3(\beta ), \end{aligned}$$

(A.13)

where $\check{\Theta }=(\check{\theta }^T(U_1)\hat{Z}_1,..., \check{\theta }^T(U_n)\hat{Z}_n)^T$, $\hat{\Theta }=({\theta }^T(U_1)\hat{Z}_1,..., {\theta }^T(U_n)\hat{Z}_n)^T$, $\hat{s}_i(\beta )=(M_{n1}(\beta ^T\hat{X}_i; \beta )$ $,..., M_{nn}(\beta ^T\hat{X}_i; \beta ))^T$, $\hat{S}_i(\beta )=(\hat{s}_1(\beta ),..., \hat{s}_n(\beta ))^T$ and $\hat{W}^{*}=diag\{I_{\mathcal {X}}(\hat{X}_1),..., I_{\mathcal {X}}(\hat{X}_n)\}$. From the proof of Theorem 1, we can show that

$$\begin{aligned} \sup \limits _{u\in {\mathcal {N}}(u_0), \beta \in {\mathcal {B}_n}}||\check{\theta }(u; \beta ){-}\theta (u)||{=}O_{P}\left( \left[ \frac{\log n}{nh_2}\right] ^{1/2}+\left[ \frac{\log n}{n h_3}\right] ^{1/2}+h_2^2+h_3^2+C_n\right) , \end{aligned}$$

where $C_n$ is defined in (A.4). Then, we can easily prove that $\Xi _2(\beta )=\Xi _0+o_{P}(n^{1/2})$ and $\Xi _3(\beta )=o_{P}(n^{1/2})$, where $\beta \in \mathcal {B}_n$ and $\Xi _0$ is a constant. Thus, $\Xi (\beta )=\Xi _1(\beta )-\Xi _0+o_{P}(n^{1/2})$. Let $Q^{*}\left( \beta ^{(r)}\right) =(-1/2)\frac{\partial \Xi \left( \beta \right) }{\partial \beta ^{(r)}}$, so we have $Q^{*}\left( \beta ^{(r)}\right) =Q\left( \beta ^{(r)}\right) +o_{P}(n^{1/2})$, where $Q(\beta ^{(r)})=(-1/2)\frac{\partial \Xi _1(\beta ^{(r)})}{\partial \beta ^{(r)}}$, namely,

$$\begin{aligned} Q(\beta ^{(r)})=\sum \limits _{i=1}^{n} I_{\mathcal {X}}(\hat{X}_i)\left[ \hat{Y}_i-\theta ^T(U_i)\hat{Z}_i-\tilde{\alpha }(\beta ^T\hat{X}_i; \beta )\right] \tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J_{\beta ^{(r)}}^T\hat{X}_i, \end{aligned}$$

(A.14)

where

$$\begin{aligned} \tilde{\alpha }(t; \beta )=\sum _{i=1}^{n}M_{ni}(t; \beta )(\hat{Y}_i-\theta ^T(U_i)\hat{Z}_i), \end{aligned}$$

and

$$\begin{aligned} \tilde{\alpha }^{\prime }(t; \beta )=\sum _{i=1}^{n}\tilde{M}_{ni}(t; \beta )(\hat{Y}_i-\theta ^T(U_i)\hat{Z}_i), \end{aligned}$$

for $\beta ^{(r)}\in \mathcal {B}_n^{*}$ with $\mathcal {B}_n^{*}=\left\{ \beta ^{(r)}: ||\beta ^{(r)}-\beta _0^{(r)}||\le C^{*}n^{1/2}\right\}$, where $C^{*}$ represents a constant. From the discussion in Sect. 2, we know that the estimator $\hat{\beta }$ can be transformed via $\hat{\beta }^{(r)}$, uniformly for $\hat{\beta }\in \mathcal {B}_n$ and $\beta ^{(r)}\in \mathcal {B}_n^{*}$. Thus, we only need to consider (A.14), which can be decomposed as

$$\begin{aligned} Q(\beta ^{(r)})&=\sum _{i=1}^{n}I_{\mathcal {X}}(\hat{X}_i)(\hat{Y}_i-Y_i)\tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J^{T}_{\beta ^{(r)}}\hat{X}_i\\&\quad -\sum _{i=1}^{n}I_{\mathcal {X}}(\hat{X}_i)\theta ^T(U_i)(\hat{Z}_i-Z_i)\tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J^{T}_{\beta ^{(r)}}\hat{X}_i\\&\quad -\sum _{i=1}^{n}I_{\mathcal {X}}(X^{*}_i)\left[ \tilde{\alpha }(\beta ^T\hat{X}_i; \beta )-\alpha (\beta _0^TX_i)\right] \tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J^{T}_{\beta ^{(r)}}\hat{X}_i\\&\quad +\sum _{i=1}^{n}I_{\mathcal {X}}(X^{*}_i)\varepsilon _i\tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J^{T}_{\beta ^{(r)}}\hat{X}_i\\&\equiv Q_1(\beta ^{(r)})-Q_2(\beta ^{(r)})-Q_3(\beta ^{(r)})+Q_4(\beta ^{(r)}), \end{aligned}$$

where $I_{\mathcal {X}}(X^{*}_i)=I_{\mathcal {X}}(\hat{X}_i)\cdot I_{\mathcal {X}}(X_i)$. For $Q_1(\beta ^{(r)})$, we have

$$\begin{aligned} Q_1(\beta ^{(r)})&=\sum _{i=1}^{n}I_{\mathcal {X}}(X^{*}_i)(\hat{Y}_i-Y_i)\alpha ^{\prime }(\beta _0^TX_i)J^{T}_{\beta ^{(r)}}(\hat{X}_i-X_i)\nonumber \\&\quad +\sum _{i=1}^{n}I_{\mathcal {X}}(X^{*}_i)(\hat{Y}_i-Y_i)\left[ \alpha ^{\prime }(\beta _0^T\hat{X}_i)-\alpha ^{\prime }(\beta _0^TX_i)\right] J^{T}_{\beta ^{(r)}}\hat{X}_i\nonumber \\&\quad +\sum _{i=1}^{n}I_{\mathcal {X}}(\hat{X}_i)(\hat{Y}_i-Y_i)\left[ \tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )-\tilde{\alpha }^{\prime }(\beta _0^T\hat{X}_i; \beta _0)\right] J^{T}_{\beta ^{(r)}}\hat{X}_i\nonumber \\&\quad +\sum _{i=1}^{n}I_{\mathcal {X}}(\hat{X}_i)(\hat{Y}_i-Y_i)\left[ \tilde{\alpha }^{\prime }(\beta _0^T\hat{X}_i; \beta _0)-\alpha ^{\prime }(\beta _0^T\hat{X}_i)\right] J^{T}_{\beta ^{(r)}}\hat{X}_i\nonumber \\&\quad +\sum _{i=1}^{n}I_{\mathcal {X}}(X_i)(\hat{Y}_i-Y_i)\alpha ^{\prime }(\beta _0^TX_i)J^{T}_{\beta ^{(r)}}X_i\nonumber \\&\equiv Q_{11}(\beta ^{(r)})+Q_{12}(\beta ^{(r)})+Q_{13}(\beta ^{(r)})+Q_{14}(\beta ^{(r)})+Q_{15}(\beta ^{(r)}). \end{aligned}$$

(A.15)

Note that $O_{P}(n\cdot C_n^2)=o_{P}(n^{1/2})$, it can be proved that $\sup \limits _{{\beta ^{(r)}}\in \mathcal {B}^{*}_n}||Q_{11}(\beta ^{(r)})||=o_{P}(n^{1/2})$ and $\sup \limits _{{\beta ^{(r)}}\in \mathcal {B}^{*}_n}||Q_{12}(\beta ^{(r)})||=o_{P}(n^{1/2})$. For any $\beta \in \mathcal {B}_n$ and $\beta ^{(r)}\in \mathcal {B}^{*}_n$, we have $||\beta -\beta _0||\le C^{*}n^{-1/2}$, $||\beta ^{(r)}-\beta ^{(r)}_0||\le C^{*}n^{-1/2}$ and $J_{\beta ^{(r)}}-J_{\beta _0^{(r)}}=O_{P}(n^{-1/2})$, which implies that

$$\begin{aligned} \hat{\beta }-\beta _0=J_{\beta _0^{(r)}}({\hat{\beta }}^{(r)}-\beta ^{(r)}_0)+O_{P}(n^{-1}). \end{aligned}$$

(A.16)

According to (A.3), for any $\beta ^{(r)}\in \mathcal {B}_n^{*}$ and $\beta \in \mathcal {B}_n$, we can prove that

$$\begin{aligned} \begin{aligned} Q_{13}(\beta ^{(r)})&=\sum _{i=1}^{n}I_{\mathcal {X}}(\hat{X}_i)(\hat{Y}_i-Y_i)\tilde{\alpha }^{\prime \prime }(\hat{X}_i^T\bar{\beta }; \bar{\beta })J^{T}_{\beta ^{(r)}}\hat{X}_i\hat{X}_i^T(\beta -\beta _0)=o_{P}(n^{1/2}), \end{aligned} \end{aligned}$$

(A.17)

where $\bar{\beta }$ is a point between $\beta$ and $\beta _0$. From Lammas 1 and 2 in Zhu and Xue (2006), we have

$$\begin{aligned} \begin{aligned} E[n^{-1}Q^2_{14}(\beta _0^{(r)})]&\le c\cdot O_{P}(C_n^2) \cdot h_4^2\\&\quad +c\cdot n^{-1}\sum _{i=1}^{n}\sum _{j=1}^{n}\sum _{k=1}^{n}(\hat{Y}_i-Y_i)(\hat{Y}_k-Y_k)E\left[ \tilde{M}_{nj}^2(\beta _0^T\hat{X}_i; \beta _0)\right] ^2\\&\le c\cdot O_{P}(C_n^2) \cdot h_4^2+c\cdot O_{P}(n\cdot C_n^{2})(nh_4^3)^{-1} \rightarrow 0. \end{aligned} \end{aligned}$$

Thus, we can obtain $\sup \limits _{{\beta ^{(r)}}\in \mathcal {B}^{*}_n}||Q_{14}(\beta ^{(r)})||=o_{P}(n^{1/2})$. Consequently, for any $\beta ^{(r)}\in \mathcal {B}_n^{*}$, we have

$$\begin{aligned} Q_1(\beta ^{(r)})=Q_{15}(\beta ^{(r)})+o_{P}(n^{1/2}). \end{aligned}$$

(A.18)

Similarly, we have

$$\begin{aligned} Q_2(\beta ^{(r)})=\sum _{i=1}^{n}I_{\mathcal {X}}(X_i)\theta ^T(U_i)(\hat{Z}_i-Z_i)\alpha ^{\prime }(\beta _0^TX_i)J^T_{\beta ^{(r)}}X_i+o_{P}(n^{1/2}), \end{aligned}$$

(A.19)

for any $\beta ^{(r)}\in \mathcal {B}_n^{*}$. Next, we deal with the $Q_3(\beta ^{(r)})$ and $Q_4(\beta ^{(r)})$. It can be proved that

$$\begin{aligned} Q_4(\beta ^{(r)})-Q_3(\beta ^{(r)})&=\sum _{i=1}^{n}I_{\mathcal {X}}(X_i)\varepsilon _i \alpha ^{\prime }(\beta _0^TX_i)J^T_{\beta ^{(r)}}\left[ X_i-E(X_i\mid \beta _0^TX_i)\right] \nonumber \\&\quad -\sum _{i=1}^{n}I_{\mathcal {X}}(X_i)\left[ \tilde{\alpha }(\beta ^TX_i; \beta )-\tilde{\alpha }(\beta _0^TX_i; \beta _0)\right] \tilde{\alpha }(\beta ^T\hat{X}_i; \beta )J^T_{\beta ^{(r)}}\hat{X}_i\nonumber \\&\quad -\sum _{i=1}^{n}I_{\mathcal {X}}(X^{*}_i)\left[ \sum _{l=1}^{p}\frac{\partial \alpha (\beta _0^TX_i)}{\partial x_l}(\hat{X}_{li}-X_{li})\right] \alpha ^{\prime }(\beta _0^TX_i)J^T_{\beta ^{(r)}}X_i\nonumber \\&\equiv Q_{31}(\beta ^{(r)})-Q_{32}(\beta ^{(r)})-Q_{33}(\beta ^{(r)})+o_{P}(n^{1/2}). \end{aligned}$$

(A.20)

By direct calculations, we have

$$\begin{aligned} \sup \limits _{\beta ^{(r)}\in \mathcal {B}_n^{*}}||Q_{31}(\beta ^{(r)})-U(\beta _0^{(r)})||=o_{P}(n^{1/2}), \end{aligned}$$

(A.21)

where

$$\begin{aligned} U(\beta _0^{(r)})=\sum _{i=1}^{n}I_{\mathcal {X}}(X_i)\varepsilon _i\alpha ^{\prime }(\beta _0^TX_i) J_{\beta _0^{(r)}}^T\left[ X_i-E\left( X_i\mid \beta _0^TX_i\right) \right] , \end{aligned}$$

uniformly for $\beta ^{(r)}\in \mathcal {B}^{*}_n$. Using Taylor’s expansion for $\tilde{\alpha }(\beta ^TX; \beta )$ at $\beta _0$ and let $\bar{\beta }=\bar{\beta }(\bar{\beta }^{(r)})$ be a suitable mean with $\bar{\beta }^{(r)}\in \mathcal {B}_n^{*}$, we have

$$\begin{aligned} Q_{32}(\beta ^{(r)})&=\sum \limits _{i=1}^{n}I_{\mathcal {X}}(X_i^{*})\tilde{\alpha }^{\prime }(X_i^T\bar{\beta }; \bar{\beta })\tilde{\alpha }^{\prime }(\beta ^T\hat{X}_i; \beta )J^T_{\bar{\beta }^{(r)}}\hat{X}_iX_i^TJ_{\beta ^{(r)}}(\beta ^{(r)}-\beta _0^{(r)}). \end{aligned}$$

From Lemma A.4 in Wang et al. (2010), we have

$$\begin{aligned} \sup \limits _{x\times \beta \in \mathcal {X}\times \mathcal {\beta }_n}||\tilde{\alpha }(\beta ^Tx; \beta )-\alpha (\beta _0^TX)||=o_{P}(1). \end{aligned}$$

According to the above equation and (A.3), we can show that

$$\begin{aligned} \sup _{\beta ^{(r)}, \bar{\beta }^{(r)}\in \mathcal {B}_n^{*}}||Q_{32}(\beta ^{(r)}, \bar{\beta }^{(r)})-n\Gamma (\beta ^{(r)}-\beta ^{(r)}_0)||=o_{P}(n^{1/2}), \end{aligned}$$

which means

$$\begin{aligned} \sup _{\beta ^{(r)}\in \mathcal {B}_n^{*}}||Q_{32}(\beta ^{(r)})-n\Gamma (\beta ^{(r)}-\beta ^{(r)}_0)||=o_{P}(n^{1/2}). \end{aligned}$$

This together with (A.15)–(A.21), we can prove that

$$\begin{aligned} \sup \limits _{\beta ^{(r)}\in \mathcal {B}_n^{*}}||Q(\beta ^{(r)})-U(\beta _0^{(r)})-\digamma (\beta _0^{(r)})+n\Gamma (\beta _0^{(r)}-\beta _0^{(r)})||=o_{P}(n^{1/2}), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \digamma (\beta _0^{(r)})&=\frac{1}{2}\sum _{i=1}^n\left[ (Y_i-E[Y])\varpi _Y-\left[ \theta ^T(U_i)Z_i-E[\theta ^T(U)Z]\right] \varpi _Z\right. \\&\left. \quad -\sum _{l=1}^{q}(X_{li}-E[X_{li}])\varpi _{X,l}\right] \\&\quad +\sum _{i=1}^n\left[ (\tilde{Y}_i-Y_i)\varpi _Y-\theta ^T(\tilde{Z}_i-Z_i)\varpi _Z-\sum _{l=1}^{q}(\tilde{X}_{li}-X_{li})\varpi _{X,l}\right] . \end{aligned} \end{aligned}$$

Let $\hat{\beta }^{(r)}\in \mathcal {B}_n^{*}$ be a solution of $Q^{*}(\beta ^{(r)})=0$, then we obtain

$$\begin{aligned} 0=U(\beta _0^{(r)})+\digamma (\beta _0^{(r)})-n\Gamma (\hat{\beta }^{(r)}-\beta _0^{(r)})+o_{P}(n^{1/2}), \end{aligned}$$

which implies

$$\begin{aligned} \sqrt{n}(\hat{\beta }^{(r)}-\beta _0^{(r)})=\sqrt{n}\Gamma ^{-1}\left[ U(\beta _0^{(r)})+\digamma (\beta _0^{(r)})\right] +o_{P}(1), \end{aligned}$$

and

$$\begin{aligned} \sqrt{n}(\hat{\beta }-\beta _0)=J_{\beta _0^{(r)}}\Gamma ^{-1}\sqrt{n}\left[ U(\beta _0^{(r)})+\digamma (\beta _0^{(r)})\right] +o_{P}(1). \end{aligned}$$

By the central limiting theorem and Slutsky’s theorem, we prove the Theorem 2. $\square$

Proof of Theorem 3

Firstly, we define

$$\begin{aligned} \hat{\kappa }_{2j}=\sum _{i=1}^{n}M_{ni}(t; \beta )\hat{Z}_{ij}. \end{aligned}$$

From (A.9) and Lamma A.4 in Zhu and Xue (2010) , we have

$$\begin{aligned} \sup \limits _{(x, \beta )\in \mathcal {X}\times \mathcal {B}}|\hat{\kappa }_{2j}(\beta ^Tx; \beta )-\kappa _{2j}(\beta ^Tx)|=o_{P}(1), \end{aligned}$$

and

$$\begin{aligned} \sup \limits _{(X, \beta ) \in \mathcal {X}\times \mathcal {B}_n}|\tilde{\alpha }(\beta ^TX; \beta )-\alpha (\beta ^TX; \beta )|=O_{P}\left( \left[ \frac{\log n}{nh_4}\right] ^{1/2}+h_4^2\right) . \end{aligned}$$

Combining Corollary 1 with the condition $h_s=cn^{-1/5}$ and $c>0$, for $s=1, 2, 3$, we can prove that

$$\begin{aligned} \sup \limits _{u\in \mathcal {N}(u_0)}||\hat{\theta }(u)-\theta (u)||=O_{P}\left( n^{-3/ 10}(\log n)\right) . \end{aligned}$$

Therefore, by simple calculation, we obtain

$$\begin{aligned}&\sup \limits _{(x\times \beta )\, \in \,\mathcal {X}\times \mathcal {B}_n}|\hat{\alpha }(\beta ^Tx)-\alpha (\beta ^Tx)|\\&\quad \le \sum _{j=1}^{q}\sup \limits _{(x\times \beta )\, \in \,\mathcal {X}\times \mathcal {B}_n}|\hat{\kappa }_{2j}(\beta ^Tx; \beta )\sup _{u\in \mathcal {N}(u_0)}|\hat{\theta }(u)-\theta (u)|\\&\qquad +q\sup \limits _{(x\times \beta )\, \in \,\mathcal {X}\times \mathcal {B}_n}|\tilde{\alpha }(\beta ^Tx; \beta )-\alpha (\beta ^Tx; \beta )|\\&\quad =O_{P}\left( \left[ \frac{\log n}{nh_4}\right] ^{1/2}+h_4^2+n^{-3/ 10}\log n\right) . \end{aligned}$$

Theorem 3 is proved immediately. $\square$