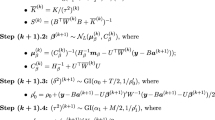Abstract
One of the advantages for the varying-coefficient model is to allow the coefficients to vary as smooth functions of other variables and the coefficients functions can be estimated easily through a simple B-spline approximations method. This leads to a simple one-step estimation procedure. We show that such a one-step method cannot be optimal when some coefficient functions possess different degrees of smoothness. Under the regularity conditions, the consistency and asymptotic normality of the two step B-spline estimators are also derived. A few simulation studies show that the gain by the two-step procedure can be quite substantial. The methodology is illustrated by an AIDS data set.



Similar content being viewed by others
References
Agarwal GG, Studden WJ (1980) Asymptotic integrated mean square error using least squares and bias minimizing spline. Ann Stat 8:1307–1325
Cai Z (2002) Two-step likelihood estimation procedure for varying-coefficient models. J Multivar Anal 82:189–209
Cai Z, Sun Y (2003) Local linear estimation for time-dependent coefficients in Coxs regression models. Scand J Stat 30:93–11
Cai Z, Fan J, Li R (2000) Efficient estimation and inferences for varying-coefficient models. J Am Stat Assoc 95:888–902
Chiang CT, Rice JA, Wu CO (2001) Smoothing spline estimation for varying coefficient models with repeatedly measured dependent variables. J Am Stat Assoc 96:605–619
DeBoor C (1978) A practical guide to splines. Springer, New York
Eubank RL, Huang C, Maldonado YM et al (2004) Smoothing spline estimation in varying-coefficient models. J R Stat Soc Ser B 66:653–667
Fan J, Li R (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. J Am Stat Assoc 96:1348–1360
Fan J, Li R (2004) New estimation and model selection procedures for semiparametric modeling in longitudinal data analysis. J Am Stat Assoc 99:710–723
Fan J, Zhang W (1999) Statistical estimation in varying coefficient models. Ann Stat 27:1491–1518
Fan J, Zhang W (2000) Simultaneous confidence bands and hypothesis testing in varying-coefficient models. Scand J Stat 27:715–731
Fan J, Zhang W (2008) Statistical methods with varying coefficient models. Stat Interface 1:179–195
Ferguson C, Bowman A, Scott E, Carvalho L (2007) Model comparison for a complex ecological system. J R Stat Soc Ser A 170:691–711
Finley A (2011) Comparing spatially-varying coefficients models for analysis of ecological data with non-stationary and anisotropic residual dependence. Methods Ecol Evol 2:143–154
Gelfand A, Kim J, Sirmans C, Banerjee S (2003) Spatial modeling with spatially varying coefficient processes. J Am Stat Assoc 98:387–396
Hastie T, Tibshirani R (1993) Varying-coefficient models. J R Stat Soc Ser B 55:757–796
He XM, Shi P (1994) Convergence rate of b-spline estimators of nonparametric conditional quantile functions. J Nonparametr Stat 3:299–308
Hoover D, Rice J, Wu C (1998) Nonparametric smoothing estimates of time-varying coefficient models with longitudinal data. Biometrika 85:809–822
Hu L, Huang T, You J (2019) Estimation and identification of a varying-coefficient additive model for locally stationary processes. J Am Stat Assoc 114:1191–1204
Huang JZ, Wu CO, Zhou L (2002) Varying-coefficient models and basis function approximations for the analysis of the analysis of repeated measurements. Biometrika 89:111–128
Ip WC, Wong H, Zhang R (2007) Generalized likelihood ratio test for varying-coefficient models with different smoothing variables. Comput Stat Data Anal 51:4543–4561
Leng C (2009) A simple approach for varying-coefficient model selection. J Stat Plan Inference 139:2138–2146
Lu YQ, Mao SS (2006) Local asymptotics for B-spline estimators of the varying coefficient model. Commun Stat-Theory Methods 33:1119–1138
Mu J, Wang G, Wang L (2018) Estimation and inference in spatially varying coefficient models. Environmetrics 29:e2485
Schumaker LL (1981) Spline functions. Wiley, New York
Tang QG, Cheng LS (2008) M-estimation and B-spline approximation for varying coefficient models with longitudinal data. J Nonparametr Stat 20:611–625
Tian L, Zucker D, Wei L (2005) On the Cox model with time-varying regression coefficients. J Am Stat Assoc 100:172–183
Wang HS, Xia YC (2009) Shrinkage estimation of the varying coefficient model. J Am Stat Assoc 104:747–757
Wang L, Li H, Huang JZ (2008) Variable selection in nonparametric varying-coefficient models for analysis of repeated measurements. J Am Stat Assoc 103:1556–1569
Xue LG, Zhu LX (2007a) Empirical likelihood for a varying coefficient model with longitudinal data. J Am Stat Assoc 102:642–652
Xue LG, Zhu LX (2007b) Empirical likelihood semiparametric regression analysis for longitudinal data. Biometrika. 94:921–937
Zhang W, Lee SY (2000) Variable bandwidth Selection in varying-coefficient models. J Multivar Anal 74:116–134
Zhao PX, Xue LG (2009) Variable selection for semiparametric varying coefficient partially linear models. Stat Probab Lett 79:2148–2157
Zhou S, Shen X, Wolfe DA (1998) Local asymptotics for regression spline and confidence regions. Ann Stat 26:1760–1782
Acknowledgements
We would like to thank the Editor and referees very much for their constructive comments which led an improved manuscript. We are very grateful to Drs. J.Z. Huang C. O. Wu and L. Zhou for allowing us to use the dataset “MACS Public Use Data Set Release PO4 (1984–1991)”. This research was supported by the National Natural Science Foundation of China (#11471264, #11361015) and the Fundamental Research Funds for the Central Universities (#JBK1806 002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proof of theorems
Appendix: Proof of theorems
It will be convenient to introduce the following notation
where \(i=1,2,\ldots ,n\), \(j=1,2,\ldots ,p\), then \(D=D_x\cdot (\pi (u_1),\pi (u_2),\ldots ,\pi (u_n))^{T}\). \(\lambda _{\max }^A\) and \(\lambda _{\min }^A\) are, respectively , the maximum and minimum eigenvalue of A. \(I_p\) is \(p\times p\) unit matrix. \(Q_n(x,u)\) is the empirical distribution of \((X_i,u_i)_{i=1}^{n}\). \(Q_n(x|u)\) is the conditional empirical distribution, \(Q_n(u)\) is the marginal empirical distribution.
Lemma 1
There exists constants \(0<c'_{1}<c'_{2}<\infty \) (independent of n and \(k_j\)) such that
Proof
By the Lemma 6.1 of Zhou et al. (1998) , there exists the constants \(0<c'_{1}<c'_{2}<\infty \) (independent of n and \(k_j\)) such that
Hence
This is, (A.1) holds. \(\square \)
Lemma 2
If condition C3 holds, there exists the constants \(0<c_1<c_2<\infty \) (independent of n and \(k_j)\) such that
Proof
By
Hence
By condition C3,
From (A.3),
From (3.2),
Let \(c_1=c'_1m_3\), \(c_2=c'_2M_3\), we have
Note that
(A.2) holds.
By Lemma 2, we also know that
\(\square \)
Lemma 3
If A and B are nonnegative matrices, then
Proof
The strategy to prove this lemma is similar to Lemma 6.5 of Zhou et al. (1998). Therefore, we omit the proof. \(\square \)
Lemma 4
If conditions C1 and C2 hold, then there exits a constant \(M_5\) such that
\(j=1,2,\ldots ,p\), where \(\alpha _j\) is a \(N_j \times 1\) vector depending on \(\beta _j(u).\)
Proof
Lemma 4 proof follows readily from Corollary 6.21 of Schumaker (1981). \(\square \)
Proof of Theorem 1
By (2.9), then
where \(\chi =(X_i,u_i)^n_{i=1}\) and \({E_\chi }\) denotes the conditional expectation given \(\chi \). So
on the other hand,
Let \(\eta (u) = G(u)(\beta (u) - s(u)) = {({\eta _1}(u), \ldots ,{\eta _p}(u))^T }\) and \({\eta _i}(u) = \sum \nolimits _{j = 1}^p {{g_{ij}}} (u)({\beta _j}(u) - {s_j}(u)),\ i=1,2\ldots ,p\). Then, \(\pi (u)G(u)(\beta (u) - s(u)) = \pi (u)\eta (u),\) by (3.1), the \(((i-1)N+l)\)th element of \(\displaystyle \int {\pi (u)} \eta (u) d{Q_n}(u)\) is
by Glivenko–Cantelli Theorem,
by \(k_j=O(n^{\frac{1}{{2m + 1}}})\), \(m>1\),
by (A.10), condition C2 and Lemma 6.10 of Agarwal et al. (1980), for any \(1\le j\le p\),
by (A.9),
Let \({D^T}{D_x}(B(U) - S(U)) = W = {(W_1^T, \ldots ,W_p^T)^T},{W_i} = {({w_{i1}}, \ldots ,{w_{i{N_j}}})^T}.\)
by Lemma 3
Hence
by (A.5), (A.7), (A.9) and (A.13),
by Lemma 4,
Hence
Now let us prove the equation
where \(V\mathrm{{a}}{\mathrm{{r}}_\chi }({{\hat{\beta }}} (u)) = {E_\chi }(({{\hat{\beta }}} (u) - {E_\chi }{{\hat{\beta }}} (u)){({E_\chi } - {E_\chi }{{\hat{\beta }}} (u))^T})\).
By (2.9),
where \({\Sigma _\beta }(u) = {\pi ^T }(u) \cdot {({D^T }D)^{ - 1}}\pi (u)\).
Let \(c\in R^{p}\) be a constant vector. By Lemma 3,
similarly,
Let \(u \in \left( {{{\pi '}_{{i_u}}},{{\pi '}_{{i_u} + 1}}} \right] \). By (2.5),
On the other hand, we have
Hence (A.16) holds.
\(\square \)
Proof of Corollary 2
The Corollary 2 follows by the proof of Theorem 1. \(\square \)
Proof of Theorem 3
Let \(c\in R^{p}\) be a constant vector. We have
by (A.15), (A.21) and \({k_j} = O({n^{\frac{1}{{2m + 1}}}}),1 \le j \le p,\)
then, it suffices to show that
Noting that
where \(\varepsilon = {({\varepsilon _1},{\varepsilon _2}, \ldots ,{\varepsilon _n})^T }\), \(A = {\pi ^T}(u) \cdot {({D^T}D)^{ - 1}}{D^T} = ({A_1},{A_2}, \ldots ,{A_n})\),
where \({b_i} = {c^\tau }{A_i}\). To check the required Lindeberg–Feller condition, it suffices to verify
By (A.21), \(\sum \nolimits _{i = 1}^n {b_i^2} = {c^T}A{A^T}c = {c^T}{\pi ^T}(u){({D^T}D)^{ - 1}}\pi (u)c = c\sum \nolimits _\beta {(u)} c = O\left( \frac{1}{{nh}}\right) .\)
On the other hand, By Lemma 3 and \(\left| {{x_i}} \right| < {M_4}\),
Hence
(A.23) holds. The proof is completed. \(\square \)
Rights and permissions
About this article
Cite this article
Jin, J., Ma, T. & Dai, J. New efficient spline estimation for varying-coefficient models with two-step knot number selection. Metrika 84, 693–712 (2021). https://doi.org/10.1007/s00184-020-00798-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00184-020-00798-8