Estimation of finite mixture models of skew-symmetric circular distributions

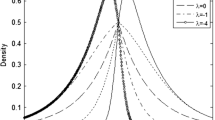
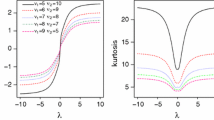
Abstract

Analysis of circular data is challenging, since the usual statistical methods are unsuitable and it is necessary to use circular periodic probabilistic models. Because some actual circular datasets exhibit asymmetry and/or multimodality, finite mixtures of symmetric circular distributions to model and fit these data have been investigated. However, it is necessary to question the predominant assumption that each component in the finite mixture model is symmetric. In this study, we consider a finite mixture model of possibly skewed circular distributions and discuss the expectation-maximization (EM) algorithm for the maximum likelihood estimate. It is shown that the maximum likelihood estimator is strongly consistent under some suitable conditions in a finite mixture of skew-symmetric circular distributions. A modified M-step in the EM algorithm is proposed in order to estimate the unknown parameter vectors effectively. To investigate the performance of our proposed model with its estimation procedure, we provide a numerical example as well as data analysis using the records of the time of day of fatal traffic accidents.

Appendices

Appendix

Proofs of the main results

In this Appendix, we provide the proofs of Theorem 1 and Proposition 1 stated in Sect. 3.

Let ${\mathcal {N}}(\varvec{\eta }):=\{ \theta \in [0,2\pi )|f^{\psi }(\theta |\varvec{\eta })=0\}$. For simplicity of exposition, we define a set of the mixing proportions $\varvec{\alpha }=(\alpha _{1}, \ldots , \alpha _{g})^{T}$ by $A:=\left\{ \varvec{\alpha }| \sum _{j=1}^{g}\alpha _{j}=1, \alpha _{j} \ge 0\right\}$, and the expectation of function $q(\theta )$ of $\theta$ on $[0,2\pi )$ under the true model $f^{\psi }(\theta |\varvec{\eta }^{0})$ by $E_{0}\{ q( \varTheta )\} :=\int _{0}^{2\pi }q(\theta )f^{\psi }(\theta |\varvec{\eta }^{0})d\theta$. Then, we present the following condition.

• [A1’] $\varGamma ^{\psi }$ is a compact subset in ${\mathbb {R}}^{(b+3)g}$ such that for any $\theta \in [0,2\pi )$, $\sup _{\varvec{\eta }\in \varGamma ^{\psi }}f^{\psi }(\theta |\varvec{\eta })<\infty$.

In addition, we define conditions [A2’]–[A5’] as conditions [A2]–[A5] with $\varvec{\eta }_{j}$, $\varvec{\eta }_{j}^{0}$, $\varvec{\eta }_{k}^{0}$, $\varvec{\eta }_{j}^{*}$, and ${\mathcal {S}}^{1}\times B$ replaced by $\varvec{\eta }$, $\varvec{\eta }^{0}$, $\varvec{\eta }^{0}$, $\varvec{\eta }^{*}$, and $\varGamma ^{\psi }$, respectively. Note that [A1’]–[A5’] are conditions imposed on the mixture model (5) whereas [A1]–[A5] are conditions on every component density.

To prove Theorem 1, we prepare two lemmas.

Lemma 1

Under conditions [A1]–[A5], [A1’]–[A5’] holds.

Proof

Let $f_{j}(\theta )$$(j=1, \ldots , g)$ be non-negative valued functions on $[0, 2\pi )$. Before verifying [A1’]–[A5’], we prepare the following inequalities.

• 1. For any $\varvec{\alpha }\in A$ and any $f_{j}(\theta )$$(j=1, \ldots , g)$,

  $$\begin{aligned} \log \sum _{j=1}^{g}\alpha _{j}f_{j}(\theta )\ge \sum _{j=1}^{g}\alpha _{j}\log f_{j}(\theta ) . \end{aligned}$$

  (A.1)

• 2. $\min _{j=1, \ldots , g}\{ f_{j}(\theta ) \} \ge 1$ implies for any $\varvec{\alpha }\in A$,

  $$\begin{aligned} \log \sum _{j=1}^{g}\alpha _{j}f_{j}(\theta ) \le \sum _{j=1}^{g}\log f_{j}(\theta ). \end{aligned}$$

  (A.2)

The former inequality follows from Jensen’s inequality and the latter is easily proved by using the facts $f_{j}(\theta )\le \max _{j=1, \ldots , g}f_{j}(\theta )$.

Because [A4’] and [A5’] are obvious, we only verify [A1’], [A2’], and [A3’]. First, we check [A1’]. We prove only that $\varGamma ^{\psi }$ is compact, because the rest is obvious. Since the ${\mathcal {S}}^{1}$, which is the range of $\varvec{\mu }_{j}$, is a closed and bounded set in ${\mathbb {R}}^{2}$, ${\mathcal {S}}^{1}$ is compact in ${\mathbb {R}}^{2}$. Because A is compact in ${\mathbb {R}}^{g}$, B is compact from [A1], and the parameter space can be expressed as a direct product from $\varGamma ^{\psi }=A\times {\mathcal {S}}^{1}\times \cdots \times {\mathcal {S}}^{1}\times B\times \cdots \times B$, $\varGamma ^{\psi }$ is also compact.

Next, we check [A2’]. It follows from inequality (A.2) that

$$\begin{aligned}&E_{0}\left[ \log \sup _{\varvec{\eta }\in U(\varvec{\eta }^{*})}\left\{ \max (f^{\psi }(\varTheta |\varvec{\eta }),1) \right\} \right] \nonumber \\&\quad \le E_{0}\left[ \log \sum _{j=1}^{g}\alpha _{j}\sup _{\varvec{\eta }\in U(\varvec{\eta }^{*})}\max (f^{\psi }(\varTheta |\varvec{\eta }_{j}),1) \right] \nonumber \\&\quad \le \sum _{j=1}^{g}E_{0}\left[ \log \sup _{\varvec{\eta }\in U(\varvec{\eta }^{*})}\max (f^{\psi }(\varTheta |\varvec{\eta }_{j}),1) \right] \nonumber \\&\quad = \sum _{j=1}^{g}\sum _{k=1}^{g}\alpha _{k}^{0}E_{\varvec{\eta }_{k}^{0}}\left[ \log \sup _{\varvec{\eta }_{j}\in U(\varvec{\eta }_{j}^{*})}\max (f^{\psi }(\varTheta |\varvec{\eta }_{j}),1) \right] , \end{aligned}$$

(A.3)

for some neighborhood $U(\varvec{\eta }_{j}^{*})$ of $\varvec{\eta }_{j}^{*}$. Then, by condition [A2], Eq. (A.3) is finite, and hence, [A2’] is verified.

Finally, we check [A3’]. Combining condition [A3] and inequality (A.1) yields $E_{0}\{ \log f^{\psi }(\varTheta |\varvec{\eta })\} \ge \sum _{j=1}^{g}\sum _{k=1}^{g}\alpha _{j}\alpha _{k}^{0}E_{\varvec{\eta }_{k}^{0}}\left\{ \log f^{\psi }(\varTheta |\varvec{\eta }_{j})\right\} >-\infty$, which completes the proof of [A3’]. $\square$

Lemma 2

Under conditions [A1’]–[A5’], it holds that for any $\varvec{\eta }^{*}\in \varGamma ^{\psi }$ with $\text {dis}\{ \varvec{\eta }^{*}, \varGamma ^{\psi }(\varvec{\eta }^{0})\} >0$ and any decreasing sequence $\{ \delta _{n}\}$ with $\delta _{n}\downarrow 0$$(n\rightarrow \infty )$,

$$\begin{aligned} \lim _{n\rightarrow \infty } E_{0}\left\{ \log \sup _{\varvec{\eta }\in U_{\delta _{n}}(\varvec{\eta }^{*})}f^{\psi }(\varTheta |\varvec{\eta }^{*})\right\}&<E_{0}\left\{ \log f^{\psi }(\varTheta |\varvec{\eta }^{0})\right\} . \end{aligned}$$

(A.4)

Proof

This is proved by the same argument as in the proof of Theorem 1 of Cheng and Liu (2001). $\square$

Proof of Theorem 1

Let $\epsilon >0$ be an arbitrary real number. Following the proof of Theorem 1 of Cheng and Liu (2001), we show that for any closed subset S of $\varGamma ^{\psi }$ with $\text {dis}\{ S, \varGamma ^{\psi }(\varvec{\eta }^{0})\} \ge \epsilon$,

$$\begin{aligned} P_{0}\left\{ \lim _{n\rightarrow \infty }\sup _{\varvec{\eta }\in S}\frac{\prod _{i=1}^{n}f^{\psi }(\varTheta _{i}|\varvec{\eta })}{\prod _{i=1}^{n}f^{\psi }(\varTheta _{i}|\varvec{\eta }^{0})}=0\right\} =1. \end{aligned}$$

By using Lemma 2 and arguing as in the proof of Theorem 2 of Wald (1949) with the Heine–Borel theorem, there exist finite points $\varvec{\eta }^{*j}\in S$$(j=1, \ldots , J)$ and their neighborhoods $U^{j}(\varvec{\eta }^{*j})$$(j=1, \ldots , J)$ such that $S\subseteq \cup _{j=1}^{J}U^{j}(\varvec{\eta }^{*j})$ and

$$\begin{aligned}&E_{0}\left\{ \log \sup _{\varvec{\eta }\in U^{j}(\varvec{\eta }^{*j})}f^{\psi }(\varTheta |\varvec{\eta })\right\} <E_{0}\left\{ \log f^{\psi }(\varTheta |\varvec{\eta }^{0})\right\} . \end{aligned}$$

(A.5)

Note that inequality (A.5) corresponds to inequality (A.4). By contrast, for any $\varvec{\eta }$, the probability that $f^{\psi }(\varTheta _{i}|\varvec{\eta })$ is zero for some $i\in {\mathbb {N}}$ is

$$\begin{aligned} P_{0}\left\{ \bigcup _{i=1}^{\infty }\{ \varTheta _{i}\in [0,2\pi )|f(\varTheta _{i}|\varvec{\eta })=0\}\right\}&\le \sum _{i=1}^{\infty }P_{0}\left\{ \varTheta _{i}\in [0,2\pi )|f(\varTheta _{i}|\varvec{\eta })=0\right\} =0. \end{aligned}$$

(A.6)

Thus, this event is a null set, and hence is negligible. Using the strong law of large numbers and inequality (A.5), we have

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^{n}\log \sup _{\varvec{\eta }\in U^{j}(\varvec{\eta }^{*j})}f(\varTheta _{i} |\varvec{\eta }) -\frac{1}{n}\sum _{i=1}^{n}\log f(\varTheta _{i} |\varvec{\eta }^{0})\nonumber \\&\quad {\mathop {\longrightarrow }\limits ^{\text {a.s.}}} E_{0}\left\{ \log \sup _{\varvec{\eta }\in U^{j}(\varvec{\eta }^{*j})}f(\varTheta |\varvec{\eta })\right\} -E_{0}\left\{ \log f(\varTheta |\varvec{\eta }^{0})\right\} <0, \end{aligned}$$

(A.7)

where the symbol ${\mathop {\longrightarrow }\limits ^{\text {a.s.}}}$ stands for almost sure convergence. Note that expression (A.7) is well-defined almost everywhere under the true probability distribution from Eq. (A.6). Thus, we have

$$\begin{aligned}&\sup _{\varvec{\eta }\in S}\frac{\prod _{i=1}^{n}f^{\psi }(\varTheta _{i}|\varvec{\eta })}{\prod _{i=1}^{n}f^{\psi }(\varTheta _{i}|\varvec{\eta }^{0})} \nonumber \\&\quad \le \sum _{j=1}^{J}\exp \left\{ n\left( \frac{1}{n}\sum _{i=1}^{n}\log \sup _{\varvec{\eta }\in U^{j}(\varvec{\eta }^{*j})}f(\varTheta _{i} |\varvec{\eta }) -\frac{1}{n}\sum _{i=1}^{n}\log f(\varTheta _{i} |\varvec{\eta }^{0})\right) \right\} \nonumber \\&\qquad {\mathop {\longrightarrow }\limits ^{\text {a.s.}}} 0\quad (n\rightarrow \infty ). \end{aligned}$$

(A.8)

The rest is proved by arguing as in the proof of Theorem 2 of Wald (1949), with the Euclidean distance $||\bullet -\theta _{0}||$ replaced by $\text {dis}\{ \bullet , \varGamma ^{\psi }(\varvec{\eta }^{0})\}$. $\square$

To prove Proposition 1, the following two lemmas are needed.

Lemma 3

For any $\alpha >0$, there exists a constant $c_{1}>0$ such that $|\log x|\le \{ 1-(x-1)^{2}\}^{-\alpha }$ for any $x\in (0,c_{1})$.

Proof

For any $x\in (0,1)$, $\{ 1-(x-1)^{2}\}^{-\alpha }>0$ holds. Hence, it suffices to show that

$$\begin{aligned} \lim _{x\rightarrow +0}\frac{|\log x|}{\{ 1-(x-1)^{2}\}^{-\alpha }}=0. \end{aligned}$$

(A.9)

This is proved by using l’Hospital’s rule. $\square$

Lemma 4

For any $\alpha \in (0,1/2)$, it follows that

$$\begin{aligned}&\int _{0}^{1}\left\{ 1-(x-1)^{2}\right\} ^{-(\alpha +1/2)}dx=\int _{1}^{2}\left\{ 1-(x-1)^{2}\right\} ^{-(\alpha +1/2)}dx \nonumber \\&\quad =\frac{1}{2}B \left( \frac{1}{2},\frac{-2\alpha +1}{2}\right) , \end{aligned}$$

(A.10)

where $B \left( \frac{1}{2},\frac{-2\alpha +1}{2}\right)$ denotes the beta function with parameters 1 / 2 and $(-2\alpha +1)/2$.

Proof

Using integration by substitution with $x-1=\sin \theta$, the left-hand side becomes $\int _{0}^{\pi /2}(\cos \theta )^{-2\alpha }d\theta$. If $\alpha <1/2$, this is represented by $(1/2)B \left( \frac{1}{2},\frac{-2\alpha +1}{2}\right)$. $\square$

Proof of Proposition 1

$\varPsi (\hat{\varvec{\gamma }}_{ML})\in \text {argmax}_{\varvec{\eta }\in \varGamma ^{\psi }}\sum _{i=1}^{n}\log f^{\psi }_{MSRS}(\theta _{i}|\varvec{\eta })$ is obvious. In addition, it follows from $\varvec{\eta }^{0}=\varPsi (\varvec{\gamma }^{0})$ that $\varPsi (\varGamma (\varvec{\gamma }^{0}))=\varGamma ^{\psi }(\varvec{\eta }^{0})$. We show that conditions [B1]–[B3] imply [A1]–[A5]. Without loss of generality, we have only to show that the first component $f_{SRS}(\theta |\varvec{\eta }_{j})$ with $j=1$ satisfies the conditions [A1]–[A5]. First, we check conditions [A1] and [A2] for density (4) with $\psi (\mu )$ replaced by $\varvec{\mu }_{1}$,

$$\begin{aligned} f^{\psi }_{SRS}(\theta |\varvec{\mu }_{1},\varvec{\rho }_{1},\lambda _{1})=c_{\varvec{\rho }_{1}}h_{\varvec{\rho }_{1}}(\psi (\theta )^{T}\varvec{\mu }_{1})2\varPi \left\{ \lambda \varvec{\mu }_{1}^{T}\begin{pmatrix}0 &{} 1\\ -1 &{} 0\end{pmatrix} \psi (\theta )\right\} , \end{aligned}$$

(A.11)

where $\varvec{\mu }_{1}=(\mu _{11},\mu _{12})^{T}\in {\mathcal {S}}^{1}$. Let ${\tilde{\mu }}_{1}:=\text {arg}(\mu _{11}+\mathrm {i}\mu _{12})$ be the argument of the complex number $\mu _{11}+\mathrm {i}\mu _{12}$. Because $0\le \varPi (x)\le 1$ and $\psi (\theta )^{T}\varvec{\mu }_{1}=\cos (\theta -{\tilde{\mu }}_{1})$, it follows from [B1] that there exists a constant $M>0$ such that for any $\theta \in [0,2\pi )$,

$$\begin{aligned}&\sup _{\varvec{\mu }_{1}\in {\mathcal {S}}^{1}, \varvec{\rho }_{1}\in K, \lambda _{1}\in [-1,1]}f^{\psi }_{SRS}(\theta |\varvec{\mu }_{1},\varvec{\rho }_{1},\lambda _{1}) \nonumber \\&\quad \le 2\sup _{\varvec{\mu }_{1}\in {\mathcal {S}}^{1}, \varvec{\rho }_{1}\in K}c_{\varvec{\rho }_{1}}h_{\varvec{\rho }_{1}}\left( \psi (\theta )^{T}\varvec{\mu }_{1}\right) \nonumber =2\sup _{\xi \in [0,2\pi ), \varvec{\rho }_{1}\in K}c_{\varvec{\rho }_{1}}h_{\varvec{\rho }_{1}}\left( \cos \xi \right) \nonumber \\&\quad \le 2M. \end{aligned}$$

(A.12)

Therefore, we have [A1]. [A2] follows from [A1] immediately.

Next, we show condition [A3], that is, $E_{\varvec{\eta }_{1}^{0}}\left\{ \log f_{SRS}^{\psi }(\varTheta |\varvec{\eta }_{1})\right\} >-\infty$ for any $\varvec{\eta }_{1}=(\varvec{\mu }_{1}^{T},\varvec{\rho }_{1}^{T},\lambda _{1})^{T}$. Because it is obvious that $\left| E_{\varvec{\eta }_{1}^{0}}\left\{ \log f_{SRS}^{\psi }(\varTheta |\varvec{\eta }_{1})\right\} \right|$ is bounded for $\varvec{\eta }_{1}$ with $-1<\lambda _{1} <1$, we have only to prove it for $\varvec{\eta }_{1}$ with $\lambda _{1} =-1$ or 1. Setting the range of $\varTheta$ to $\{ \theta |{\tilde{\mu }}_{1}\le \theta <{\tilde{\mu }}_{1} +2\pi \}$ and applying integration by parts with $\theta ={\tilde{\theta }}-{\tilde{\mu }}_{1}$ yield

$$\begin{aligned}&E_{\varvec{\eta }_{1}^{0}}\left[ \log f_{SRS}^{\psi }(\varTheta |\varvec{\eta }_{1})\right] \nonumber \\&\quad =\int _{{\tilde{\mu }}_{1}}^{{\tilde{\mu }}_{1}+2\pi }\log \left[ f_{0}({\tilde{\theta }}|{\tilde{\mu }}_{1},\varvec{\rho }_{1})2\varPi \left\{ \lambda _{1}\sin ({\tilde{\theta }}-{\tilde{\mu }}_{1})\right\} \right] f_{SRS}^{\psi }({\tilde{\theta }}|\varvec{\eta }_{1}^{0})d{\tilde{\theta }} \nonumber \\&\quad =\int _{0}^{2\pi }\log \left[ f_{0}(\theta |0,\varvec{\rho }_{1})2\varPi \left( \lambda _{1}\sin \theta \right) \right] f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta , \end{aligned}$$

(A.13)

where the function $f_{0}$ is defined in [B1]. Here, we consider the case $\lambda _{1}=-1$. Then, Eq. (A.13) becomes

$$\begin{aligned}&\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }\log \left[ f_{0}(\theta |0,\varvec{\rho }_{1})2\varPi \left\{ (-1)\sin \theta \right\} \right] f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \end{aligned}$$

(A.14)

$$\begin{aligned}&\quad +\,\int _{[0,2\pi )\backslash [\pi /2-\epsilon , \pi /2+\epsilon ]}\log \left[ f_{0}(\theta |0,\varvec{\rho }_{1})2\varPi \left\{ (-1)\sin \theta \right\} \right] f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta , \end{aligned}$$

(A.15)

where $\epsilon >0$ is an arbitrary positive number. In (A.14), it follows from [B3] that there exist $s_{j}>0$$(j=1,2,3)$ such that for any $\theta$ with $1-s_{3}<\sin \theta \le 1$,

$$\begin{aligned} \varPi \left\{ (-1)\sin \theta \right\} \ge s_{1}\{ 1+(-1)\sin \theta \}^{s_{2}}. \end{aligned}$$

(A.16)

Hence, we choose $\epsilon >0$ for the interval $[\pi /2-\epsilon , \pi /2+\epsilon ]$ of $\theta$ to be a subset in the set $\{ \theta \in [0,2\pi )|1-s_{3}<\sin \theta \le 1\}$. Meanwhile, since $\varPi (x)$ is an increasing function in $x\in {\mathbb {R}}$, it follows that for any $\theta \in [0,2\pi )\backslash [\pi /2-\epsilon , \pi /2+\epsilon ]$

$$\begin{aligned} \varPi \left\{ (-1)\sin \theta \right\} \ge \varPi \left\{ (-1)\sin (\pi /2-\epsilon ) \right\} . \end{aligned}$$

(A.17)

By applying inequalities (A.16) and (A.17) to terms (A.14) and (A.15), respectively, Eq. (A.13) is bounded below by

$$\begin{aligned}&\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }\log \left[ f_{0}(\theta |0,\varvec{\rho }_{1})2s_{1}\{ 1+(-1)\sin \theta \}^{s_{2}}\right] f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\quad + \int _{[0,2\pi )\backslash [\pi /2-\epsilon , \pi /2+\epsilon ]}\log \left[ f_{0}(\theta |0,\varvec{\rho }_{1})2\varPi \left\{ (-1)\sin (\pi /2-\epsilon )\right\} \right] f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta . \end{aligned}$$

(A.18)

Therefore, it suffices to show that the absolute value of Eq. (A.18) is finite. The absolute value of Eq. (A.18) is bounded above by

$$\begin{aligned}&\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }\left| \log f_{0}(\theta |0,\varvec{\rho }_{1})\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad +\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }\left| \log \{ 2s_{1}(1+(-1)\sin \theta )^{s_{2}}\}\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad + \int _{[0,2\pi )\backslash [\pi /2-\epsilon , \pi /2+\epsilon ]}\left| \log f_{0}(\theta |0,\varvec{\rho }_{1})\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad +\underbrace{\left| \log 2\varPi \left\{ (-1)\sin (\pi /2-\epsilon )\right\} \right| }_{M_{\epsilon }} \int _{[0,2\pi )\backslash [\pi /2-\epsilon , \pi /2+\epsilon ]} f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\quad \le \int _{0}^{2\pi }\left| \log f_{0}(\theta |0,\varvec{\rho }_{1})\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad +\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }|\log (2s_{1})| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad +\int _{\pi /2-\epsilon }^{\pi /2+\epsilon }s_{2}\left| \log \{ 1+(-1)\sin \theta \}\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta +M_{\epsilon }\nonumber \\&\quad \le \int _{0}^{2\pi }\left| \log f_{0}(\theta |0,\varvec{\rho }_{1})\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \end{aligned}$$

(A.19)

$$\begin{aligned}&\qquad +s_{2}\int _{0}^{2\pi }\left| \log \{ 1+(-1)\sin \theta \}\right| f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})d\theta \nonumber \\&\qquad +|\log 2s_{1}|+M_{\epsilon }. \end{aligned}$$

(A.20)

By [B1], $|\log f_{0}(\theta |0,\varvec{\rho }_{1})|\le \log M$ for some constant $M>1$, and hence, integral (A.19) is bounded above by $\log M$. Next, we evaluate term (A.20). Let $\varvec{\mu }_{1}^{0}=(\mu _{11}^{0},\mu _{12}^{0})^{T}\in {\mathcal {S}}^{1}$ and let ${\tilde{\mu }}_{1}^{0}:=\text {arg}(\mu _{11}^{0}+\mathrm {i}\mu _{12}^{0})$. Then, we have

$$\begin{aligned} f_{SRS}^{\psi }(\theta +{\tilde{\mu }}_{1}|\varvec{\eta }_{1}^{0})&=c_{\varvec{\rho }_{1}^{0}}h_{\varvec{\rho }_{1}^{0}}(\cos (\theta +{\tilde{\mu }}_{1}-{\tilde{\mu }}_{1}^{0}))\left\{ 1+\lambda _{1}^{0}\sin (\theta +{\tilde{\mu }}_{1}-{\tilde{\mu }}_{1}^{0})\right\} \nonumber \\&=f_{SRS}(\theta |{\tilde{\mu }}_{1}^{0}-{\tilde{\mu }}_{1},\varvec{\rho }_{1}^{0},\lambda _{1}^{0}) \le M_{2},\qquad \text {for some }M_{2}>0, \end{aligned}$$

where the last inequality holds from [B1]. Hence, the integral part in (A.20) is bounded above by

$$\begin{aligned}&M_{2} \int _{0}^{2\pi }|\log \left\{ 1+\lambda _{1} \sin (\theta )\right\} |d\theta \nonumber \\&\quad \le M_{2} \int _{[0,\pi /2)\cup [3\pi /2, 2\pi )}|\log \left\{ 1+\lambda _{1} \sin (\theta )\right\} |d\theta +M_{2} \int _{\pi /2}^{3\pi /2} |\log \left\{ 1+\lambda _{1} \sin (\theta )\right\} |d\theta \nonumber \\&\quad =M_{2} \int _{-\pi /2}^{\pi /2}|\log \left\{ 1+\lambda _{1} \sin (\theta )\right\} |d\theta +M_{2} \int _{\pi /2}^{3\pi /2} |\log \left\{ 1+\lambda _{1} \sin (\theta )\right\} |d\theta . \end{aligned}$$

(A.21)

We evaluate the first term in (A.21). For $x=1+\lambda _{1} \sin \theta$$(\lambda _{1}\ne 0)$, we have $(d \theta /dx)=\text {sgn} (\lambda _{1} )/ \sqrt{1-(x-1)^{2}}$, where $\text {sgn} (\lambda _{1})=1$ if $\lambda _{1}>0$, and $-1$ if $\lambda _{1}<0$.

Because $\lambda _{1}=-1$, for any $c\in [0,2]$, the first term in (A.21) is

$$\begin{aligned}&M_{2}\int _{0}^{2}|\log x|\frac{1}{\sqrt{1-(x-1)^{2}}}dx \nonumber \\&\quad =M_{2}\int _{0}^{c}|\log (x)|\frac{1}{\sqrt{1-(x-1)^{2}}}dx +M_{2}\int _{c}^{2}|\log (x)|\frac{1}{\sqrt{1-(x-1)^{2}}}dx. \end{aligned}$$

(A.22)

Using Lemma 3, we choose $\alpha \in (0,1/2)$ and $c\in (0,1)$ such that expression (A.22) is bounded above by

$$\begin{aligned}&M_{2}\int _{0}^{c}\frac{1}{\{ 1-(x-1)^{2}\}^{\alpha }}\frac{1}{\sqrt{1-(x-1)^{2}}}dx+M_{2}\log 2\int _{c}^{2}\frac{1}{\sqrt{1-(x-1)^{2}}}dx \\&\quad =M_{2}\int _{0}^{c}\{ 1-(x-1)^{2}\}^{-\alpha -1/2}dx+M_{2}\log 2\int _{c}^{2}\{1-(x-1)^{2}\}^{-1/2}dx \\&\quad \le M_{3}\qquad \hbox { for some}\ M_{3}>0, \end{aligned}$$

where the last inequality holds from Lemma 4.

Hence, the first term in (A.21) is bounded. By the same argument, the second term in Eq. (A.21) is bounded, and hence, [A3] is verified under $\lambda _{1}=-1$. Because the case $\lambda _{1} =1$ is similarly proved, [A3] holds under assumptions [B1]–[B3]. [A4] is obvious from [B2]. Finally, we check condition [A5]. If $\lambda _{1}=-1$, then $\mathcal{N}(\varvec{\eta }_{1})$, which is defined in assumptions [A1]–[A5], becomes a single-point set and hence, $P_{0}\{ \mathcal{N}(\varvec{\eta }_{1})\}=0$. If $\lambda _{1}=1$, then $\mathcal{N}(\varvec{\eta }_{1})$ also becomes a single-point set. Hence, [A5] holds, which completes the verification of [A1]–[A5].

Finally, we prove the uniform convergence (14). By property 1 of Cheng and Liu (2001), if Eq. (13) in Proposition 1 holds, then there exists a sequence $\{ \varvec{\eta }_{n}^{0}\}\subseteq \varGamma ^{\psi }(\varvec{\eta }^{0})$ in which $||\varPsi (\hat{\varvec{\gamma }}_{ML})-\varvec{\eta }_{n}^{0}||\longrightarrow 0$ a.s. $P_{0}$. Therefore, it follows from the Lipschitz condition that there exists a constant $M_{4}>0$ independent of $\theta$ such that

$$\begin{aligned}&\sup _{\theta \in [0,2\pi )}|f(\theta |\hat{\varvec{\gamma }}_{ML})-f(\theta |\varvec{\gamma }^{0})| \le \sup _{\theta \in [0,2\pi )}|f^{\psi }(\theta |\varPsi (\hat{\varvec{\gamma }}_{ML}))-f^{\psi }(\theta |\varvec{\eta }_{n}^{0})| \\&\quad \le \sup _{\theta \in [0,2\pi )}M_{4} ||\varPsi (\hat{\varvec{\gamma }}_{ML})-\varvec{\eta }_{n}^{0}|| \longrightarrow 0\qquad (n\rightarrow \infty ),\quad {a.s.}~P_{0} \end{aligned}$$

which completes the proof. $\square$

Proof of Proposition 2

To prove Proposition 2, we give the following lemma.

Lemma 5

• (a) For any $\zeta \in (-2\pi , 2\pi )\backslash \{ 0 \}$,

  $$\begin{aligned} \frac{1}{n}\sum _{p=0}^{n-1}\exp (\mathrm {i}p\zeta ) \rightarrow 0 \qquad (n\rightarrow \infty ). \end{aligned}$$

• (b) For any $\xi \in {\mathbb {R}}$ and r with $0\le r<1$,

  $$\begin{aligned} \frac{1}{n}\sum _{p=0}^{n-1}\exp (\mathrm {i}p\xi )r^{p} \rightarrow 0 \qquad (n\rightarrow \infty ). \end{aligned}$$

The proof is elementary and hence, is omitted. The proof is also available from the corresponding author on request.

Proof of Proposition 2

Here, we use the characteristic function of the SSWC distribution

$$\begin{aligned} E\left\{ \exp (\mathrm {i}p\varTheta )\right\}&=E\left\{ \cos (p\varTheta )\right\} +\mathrm {i} E\left\{ \sin (p\varTheta )\right\} \nonumber \\&=\exp (\mathrm {i}p\mu )\left\{ \rho ^{|p|}+\mathrm {i}(\rho ^{|p-1|}-\rho ^{|p+1|})\frac{\lambda }{2}\right\} . \end{aligned}$$

(A.23)

For simplicity, if $p\in {\mathbb {N}}$, (A.23) is written as $E\left\{ \exp (\mathrm {i}p\varTheta )\right\} =\exp (\mathrm {i}p\mu )\rho ^{p}H(\rho , \lambda )$ where $H(\rho , \lambda )=1+\mathrm {i}(\rho ^{-1}-\rho )\lambda /2$.

Assume that for any $\varvec{\gamma }_{1}$ and $\varvec{\gamma }_{1}^{*}$ in $\varGamma _{mswc}^{\dag }$,

$$\begin{aligned}&\alpha _{1}f_{swc}(\theta |\mu _{1},\rho _{1},\lambda _{1})+\alpha _{2}f_{swc}(\theta |\mu _{2},\rho _{2},\lambda _{2})\nonumber \\&\quad =\alpha _{1}^{*}f_{swc}(\theta |\mu _{1}^{*},\rho _{1}^{*},\lambda _{1}^{*})+\alpha _{2}^{*}f_{swc}(\theta |\mu _{2}^{*},\rho _{2}^{*},\lambda _{2}^{*}). \end{aligned}$$

(A.24)

We divide the proof into the following four steps, and give the proof for each step under assumption (A.24).

Step 1:

(A.24) implies $\rho _{1}<\rho _{2}^{*}$ and $\rho _{1}^{*}<\rho _{2}$.

Step 2:

(A.24) and the result of Step 1 imply $\rho _{2}=\rho _{2}^{*}$.

Step 3:

(A.24) and the results of Steps 1–2 imply $\mu _{2}=\mu _{2}^{*}$.

Step 4:

(A.24) and the results of Steps 1–3 imply $\alpha _{2}=\alpha _{2}^{*}$ and $\lambda _{2}=\lambda _{2}^{*}$.

Proof of Step 1

We employ proof by contradiction. Assume that $\rho _{1}\ge \rho _{2}^{*}$. Then, we have $\rho _{1}^{*}<\rho _{2}^{*}\le \rho _{1}<\rho _{2}$. Taking the characteristic functions of both sides in Eq. (A.24), letting $p\ge 1$ and dividing it by $\exp (\mathrm {i}p\mu _{2})\rho _{2}^{p}$ yields

$$\begin{aligned}&\alpha _{1}\exp ( \mathrm {i}p(\mu _{1}-\mu _{2}))\left( \frac{\rho _{1}}{\rho _{2}} \right) ^{p}H(\rho _{1},\lambda _{1})+\alpha _{2}H(\rho _{2},\lambda _{2}) \nonumber \\&\quad =\alpha _{1}^{*}\exp (\mathrm {i}p(\mu _{1}^{*}-\mu _{2}))\left( \frac{\rho _{1}^{*}}{\rho _{2}} \right) ^{p}H(\rho _{1}^{*},\lambda _{1}^{*})\nonumber \\&\qquad +\alpha _{2}^{*}\exp ( \mathrm {i}p(\mu _{2}^{*}-\mu _{2}))\left( \frac{\rho _{2}^{*}}{\rho _{2}} \right) ^{p}H(\rho _{2}^{*},\lambda _{2}^{*}). \end{aligned}$$

(A.25)

Because $\left| \exp ( \mathrm {i}p(\mu _{1}-\mu _{2}))(\rho _{1}/\rho _{2})^{p}\right| \le (\rho _{1}/\rho _{2})^{p}\rightarrow 0$$(p\rightarrow \infty )$, letting $p\rightarrow \infty$, we have $\alpha _{2}H(\rho _{2},\lambda _{2})=0$. We have $\alpha _{2}=0$ because of $H(\rho _{2},\lambda _{2})\ne 0$, which contradicts assumption $\alpha _{2}>0$. The case of $\rho _{1}^{*}<\rho _{2}$ is similarly proved.

Proof of Step 2

In this step, we also employ proof by contradiction. Assume that $\rho _{2}\ne \rho _{2}^{*}$. First, we consider the case $\rho _{2}<\rho _{2}^{*}$.

Taking the characteristic functions of both sides in Eq. (A.24), letting $p\ge 1$ and dividing it by $\exp (\mathrm {i}p\mu _{2}^{*})\rho _{2}^{*p}$ yields

$$\begin{aligned}&\alpha _{1}\exp ( \mathrm {i}p(\mu _{1}-\mu _{2}^{*}))\left( \frac{\rho _{1}}{\rho _{2}^{*}} \right) ^{p}H(\rho _{1},\lambda _{1})\nonumber \\&\qquad +\alpha _{2}\exp ( \mathrm {i}p(\mu _{2}-\mu _{2}^{*}))\left( \frac{\rho _{2}}{\rho _{2}^{*}} \right) ^{p}H(\rho _{2},\lambda _{2}) \nonumber \\&\quad =\alpha _{1}^{*}\exp (\mathrm {i}p(\mu _{1}^{*}-\mu _{2}^{*}))\left( \frac{\rho _{1}^{*}}{\rho _{2}^{*}} \right) ^{p}H(\rho _{1}^{*},\lambda _{1}^{*})+\alpha _{2}^{*}H(\rho _{2}^{*},\lambda _{2}^{*}). \end{aligned}$$

(A.26)

Using the result of Step 1 and taking $p\rightarrow \infty$, we have $0=\alpha _{2}^{*}H(\rho _{2}^{*},\lambda _{2}^{*})$. Because $H(\rho _{2}^{*},\lambda _{2}^{*})\ne 0$, we have $\alpha _{2}^{*}=0$, which contradicts the assumption. The case of $\rho _{2}^{*}<\rho _{2}$ is similarly proved.

Proof of Step 3

In the third step, we also employ proof by contradiction. Assume that $\mu _{2}\ne \mu _{2}^{*}$.

Substituting the result ($\rho _{2}=\rho _{2}^{*}$) of Step 2 in Eq. (A.26) yields

$$\begin{aligned}&\alpha _{1}\exp ( \mathrm {i}p(\mu _{1}-\mu _{2}^{*}))\left( \frac{\rho _{1}}{\rho _{2}} \right) ^{p}H(\rho _{1},\lambda _{1})+\alpha _{2}\exp ( \mathrm {i}p(\mu _{2}-\mu _{2}^{*}))H(\rho _{2},\lambda _{2}) \nonumber \\&\quad =\alpha _{1}^{*}\exp (\mathrm {i}p(\mu _{1}^{*}-\mu _{2}^{*}))\left( \frac{\rho _{1}^{*}}{\rho _{2}} \right) ^{p}H(\rho _{1}^{*},\lambda _{1}^{*})+\alpha _{2}^{*}H(\rho _{2},\lambda _{2}^{*}). \end{aligned}$$

(A.27)

Because this equation holds for each $p\in {\mathbb {N}}$, we have

$$\begin{aligned}&\alpha _{1}\left\{ \frac{1}{n}\sum _{p=0}^{n-1}\exp ( \mathrm {i}p(\mu _{1}-\mu _{2}^{*}))\left( \frac{\rho _{1}}{\rho _{2}} \right) ^{p}\right\} H(\rho _{1},\lambda _{1})\nonumber \\&\qquad +\alpha _{2}\left\{ \frac{1}{n}\sum _{p=0}^{n-1}\exp ( \mathrm {i}p(\mu _{2}-\mu _{2}^{*}))\right\} H(\rho _{2},\lambda _{2}) \nonumber \\&\qquad -\frac{1}{n}\alpha _{1}H(\rho _{1},\lambda _{1})-\frac{1}{n}\alpha _{2}H(\rho _{2},\lambda _{2})\nonumber \\&\quad =\alpha _{1}^{*}\left\{ \frac{1}{n}\sum _{p=0}^{n-1}\exp (\mathrm {i}p(\mu _{1}^{*}-\mu _{2}^{*}))\left( \frac{\rho _{1}^{*}}{\rho _{2}} \right) ^{p}\right\} H(\rho _{1}^{*},\lambda _{1}^{*})+\frac{n-1}{n}\alpha _{2}^{*}H(\rho _{2},\lambda _{2}^{*}) \nonumber \\&\qquad -\frac{1}{n}\alpha _{1}^{*}H(\rho _{1}^{*},\lambda _{1}^{*}). \end{aligned}$$

(A.28)

Because $\mu _{2}-\mu _{2}^{*}$ is a value in $(-2\pi , 2\pi )\backslash \{ 0\}$, as $n\rightarrow \infty$, it follows from Lemma 5 that $\alpha _{2}^{*}H(\rho _{2},\lambda _{2}^{*})=0$. Hence, from $H(\rho _{2},\lambda _{2}^{*})\ne 0$, we have $\alpha _{2}^{*}=0$, which contradicts $\alpha _{2}^{*}>0$. Hence, we have $\mu _{2}\ne \mu _{2}^{*}$.

Proof of Step 4

Substituting the results ($\rho _{2}=\rho _{2}^{*}$ and $\mu _{2}=\mu _{2}^{*}$) of Steps 2 and 3 in Eq. (A.28) yields

$$\begin{aligned}&\alpha _{1}\exp ( \mathrm {i}p(\mu _{1}-\mu _{2}))\left( \frac{\rho _{1}}{\rho _{2}} \right) ^{p}H(\rho _{1},\lambda _{1})+\alpha _{2}H(\rho _{2},\lambda _{2}) \nonumber \\&\quad =\alpha _{1}^{*}\exp (\mathrm {i}p(\mu _{1}^{*}-\mu _{2}))\left( \frac{\rho _{1}^{*}}{\rho _{2}} \right) ^{p}H(\rho _{1}^{*},\lambda _{1}^{*})+\alpha _{2}^{*}H(\rho _{2},\lambda _{2}^{*}). \end{aligned}$$

(A.29)

Letting $p\rightarrow \infty$ in this equation, we have $\alpha _{2}H(\rho _{2},\lambda _{2})=\alpha _{2}^{*}H(\rho _{2},\lambda _{2}^{*})$. By comparing the real and imaginary parts, $\alpha _{2}=\alpha _{2}^{*}$ and $\lambda _{2}=\lambda _{2}^{*}$.

Through Steps 1–4, we have $\alpha _{1}f_{swc}(\theta |\mu _{1},\rho _{1},\lambda _{1})=\alpha _{1}^{*}f_{swc}(\theta |\mu _{1}^{*},\rho _{1}^{*},\lambda _{1}^{*})$. Because the integral from 0 to $2\pi$ of each $f_{swc}(\theta |\mu _{j},\rho _{j},\lambda _{j})$ is one, we have $\alpha _{1}=\alpha _{1}^{*}$ and hence, $f_{swc}(\theta |\mu _{1},\rho _{1},\lambda _{1})=f_{swc}(\theta |\mu _{1}^{*},\rho _{1}^{*},\lambda _{1}^{*})$. Consequently, using the identifiability of SSWC distribution (Miyata et al. 2019), we obtain $(\mu _{1},\rho _{1},\lambda _{1})^{T}=(\mu _{1}^{*},\rho _{1}^{*},\lambda _{1}^{*})^{T}$, which completes the proof. $\square$