Skip to main content
SpringerLink
Log in

Reliability of a coherent system equipped with two cold standby components

  • Published:
Metrika Aims and scope Submit manuscript

Abstract

In this paper, we focus on a particular type of coherent system which may fail either on the failure of its first component or on the failure of its second component. We investigate the renewal of such a coherent system using two cold standby components. We obtain the reliability function of the considered coherent system which is equipped with two cold standby components. We study the problem to optimize the reliability of the system. Some stochastic ordering results are also presented. Examples are provided to illustrate the theoretical results presented in this study. Our results subsume some of the earlier results in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Arriaza A, Navarro J, Suárez-Llorens A (2018) Stochastic comparisons of replacement policies in coherent systems under minimal repair. Nav Res Logist 65(6–7):550–565

    Article  MathSciNet  Google Scholar 

  • Asadi M, Berred A (2012) On the number of failed components in a coherent operating system. Stat Probab Lett 82(12):2156–2163

    Article  MathSciNet  Google Scholar 

  • Boland PJ (2001) Signatures of indirect majority systems. J Appl Probab 38(2):597–603

    Article  MathSciNet  Google Scholar 

  • Eryilmaz S (2012) On the mean residual life of a k-out-of-n: G system with a single cold standby component. Eur J Oper Res 222(2):273–277

    Article  MathSciNet  Google Scholar 

  • Eryilmaz S (2014a) A new look at dynamic behavior of binary coherent system from a state-level perspective. Ann Oper Res 212(1):115–125

    Article  MathSciNet  Google Scholar 

  • Eryilmaz S (2014b) A study on reliability of coherent systems equipped with a cold standby component. Metrika 77(3):349–359

    Article  MathSciNet  Google Scholar 

  • Eryilmaz S (2017) The effectiveness of adding cold standby redundancy to a coherent system at system and component levels. Reliab Eng Syst Saf 165:331–335

    Article  Google Scholar 

  • Khaledi BE, Shaked M (2007) Ordering conditional lifetimes of coherent systems. J Stat Plan Inference 137(4):1173–1184

    Article  MathSciNet  Google Scholar 

  • Mahmoudi M, Asadi M (2011) The dynamic signature of coherent systems. IEEE Trans Reliab 60(4):817–822

    Article  Google Scholar 

  • Mirjalili A, Sadegh MK, Rezaei M (2017) A note on the mean residual life of a coherent system with a cold standby component. Commun Stat Theory Methods 46(20):10348–10358

    Article  MathSciNet  Google Scholar 

  • Navarro J, Rubio R (2009) Computations of signatures of coherent systems with five components. Commun Stat Simul Comput 39(1):68–84

    Article  MathSciNet  Google Scholar 

  • Navarro J, Samaniego FJ, Balakrishnan N (2011) Signature-based representations for the reliability of systems with heterogeneous components. J Appl Probab 48(3):856–867

    Article  MathSciNet  Google Scholar 

  • Samaniego FJ (2007) System signatures and their applications in engineering reliability, vol 110. Springer, Berlin

    Book  Google Scholar 

  • Van Gemund AJ, Reijns GL (2012) Reliability analysis of \( k \)-out-of-\( n \) systems with single cold standby using pearson distributions. IEEE Trans Reliab 61(2):526–532

    Article  Google Scholar 

  • Wang Y (2016) Conditional k-out-of-n systems with a cold standby component. Commun Stat Theory Methods 45(21):6253–6262

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the editor, the associate editor and the anonymous referees for the useful suggestions which helped improve the presentation of the paper to a great extent. The first author would also like to thank Indian Institute of Technology Kharagpur for the financial assistance.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur, 721302, India

    Achintya Roy & Nitin Gupta

Authors
  1. Achintya Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nitin Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Achintya Roy.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Proof of Theorem 2

The reliability function of a coherent system with two cold standby components can be written as

$$\begin{aligned}&P(T_{R}(Z_{1},Z_{2})>t)\nonumber \\&\quad =P(T_{R}(Z_{1},Z_{2})>t,T=X_{1:n})\nonumber \\&\quad \quad +P(T_{R}(Z_{1},Z_{2})>t,T=X_{2:n}) +P(T_{R}(Z_{1},Z_{2})>t,T>X_{2:n})\nonumber \\&\quad =p_{1}P(T+\phi (X^{'}_{1},\ldots ,X^{'}_{u-1},Z_{1},X^{'}_{u+1},\ldots ,X^{'}_{n})>t|T=X_{1:n})\nonumber \\&\quad \quad +p_{2}P(T + \phi (X^{''}_{1},\ldots ,X^{''}_{v-1},Z_{1},X^{''}_{v+1},\ldots ,X^{''}_{w(v)-1},Z_{2},\nonumber \\&\quad X^{''}_{w(v)+1},\ldots ,X^{''}_{n})>t|T=X_{2:n})\nonumber \\&\quad \quad +\sum _{i=3}^{n} p_{i} P(X_{i:n}>t). \end{aligned}$$
(19)

Using Eq. (4) of Eryilmaz (2014b), we can write

$$\begin{aligned}&P(T+\phi (X^{ '}_{1},\ldots ,X^{'}_{u-1},Z_{1},X^{'}_{u+1},\ldots ,X^{'}_{n})>t|T=X_{1:n})= P(X_{1:n}>t) \nonumber \\&\quad \quad + \sum _{i=1}^{n} P(u=i) \int _{0}^{t} P\{ \phi (X^{'}_{1},\ldots ,X^{'}_{i-1},Z_{1},X^{'}_{i+1},\ldots ,X^{'}_{n})\nonumber \\&\quad >t-x|X_{1:n}=x\} f_{X_{1:n}}(x) dx. \end{aligned}$$
(20)

Next, consider the conditional probability in (19),

$$\begin{aligned}&P(T+\phi (X^{''}_{1},\ldots ,X^{''}_{v-1},Z_{1},X^{''}_{v+1},\ldots ,X^{''}_{w(v)-1},Z_{2},X^{''}_{w(v)+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad>t|T=X_{2:n})=\frac{1}{P(T=X_{2:n})} \nonumber \\&\quad \times P\{T+\phi (X^{''}_{1}\ldots ,X^{''}_{v-1},Z_{1},X^{''}_{v+1},\ldots ,X^{''}_{w(v)-1},Z_{2},X^{''}_{w(v)+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad>t,T=X_{2:n}\}=\frac{1}{P(T=X_{2:n})} \nonumber \\&\quad \times \sum _{i=1}^{n} P\{T+\phi (X^{''}_{1}\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{w(i)-1},Z_{2},X^{''}_{w(i)+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad>t,X_{1:n}=X_{i},T=X_{2:n}\} =\frac{1}{P(T=X_{2:n})} \nonumber \\&\quad \times \sum _{i=1}^{n}\sum _{j\ne i} ^{n} P\{\phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2},X^{''}_{j+1},\ldots ,X^{''}_{n}) +T\nonumber \\&\qquad>t,X_{1:n}=X_{i},X_{2:n}=X_{j},T=X_{2:n}\} =\frac{1}{P(T=X_{2:n})} \nonumber \\&\quad \times \sum _{i=1}^{n}\sum _{j\ne i} ^{n} P\{\phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2},X^{''}_{j+1},\ldots ,X^{''}_{n}) +X_{j}\nonumber \\&\qquad>t,X_{1:n}=X_{i},X_{2:n}=X_{j},T=X_{2:n}\} \nonumber \\&\qquad =\sum _{i=1}^{n}\sum _{j\ne i} ^{n} \frac{P(X_{1:n}=X_{i},X_{2:n}=X_{j},T=X_{2:n})}{P(T=X_{2:n})}\nonumber \\&\quad \times P\{ \phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2},X^{''}_{j+1},\ldots ,X^{''}_{n}) +X_{j}\nonumber \\&\qquad>t|X_{1:n}=X_{i},X_{2:n}=X_{j},T=X_{2:n}\} =\sum _{i=1}^{n}\sum _{j\ne i} ^{n}P(v=i) P(w(i)=j) \nonumber \\&\quad \times \int _{0}^{\infty } P\{ \phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2}, X^{''}_{j+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad>t-x|X_{2:n}=x\} f_{X_{2:n}}(x) dx = \sum _{i=1}^{n}\sum _{j\ne i}^{n} P(v=i) P(w(i)=j)\nonumber \\&\qquad \int _{t}^{\infty } f_{X_{2:n}}(x) dx + \sum _{i=1}^{n}\sum _{j\ne i}^{n} P(v=i) P(w(i)=j) \nonumber \\&\quad \times \int _{0}^{t} P\{ \phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2},X^{''}_{j+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad>t-x|X_{2:n}=x\} f_{X_{2:n}}(x) dx = P(X_{2:n}>t) + \sum _{i=1}^{n}\sum _{j\ne i}^{n} P(v=i)P(w(i)=j)\nonumber \\&\quad \times \int _{0}^{t} P\{ \phi (X^{''}_{1},\ldots ,X^{''}_{i-1},Z_{1},X^{''}_{i+1},\ldots ,X^{''}_{j-1},Z_{2},X^{''}_{j+1},\ldots ,X^{''}_{n})\nonumber \\&\qquad >t-x|X_{2:n}=x\} f_{X_{2:n}}(x) dx. \end{aligned}$$
(21)

Therefore, using Eqs. (20) and (21) in (19), we have Eq. (4). \(\square \)

Proof of equation (13)

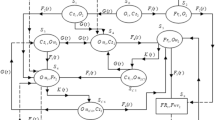
By the definition of five-component bridge system,

$$\begin{aligned}&P\{ \phi (Z_{1},Z_{2},X^{''}_{3},X^{''}_{4},X^{''}_{5})>t-x|X_{2:5}=x\} \\&\quad =P(min(Z_{1},X^{''}_{4})>t-x|X_{2:5}=x)\\&\qquad +P(min(Z_{2},X^{''}_{5})>t-x|X_{2:5}=x)\\&\qquad +P(min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x|X_{2:5}=x)\\&\qquad +P(min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x)\\&\qquad -P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\qquad -P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x|X_{2:5}=x\}\\&\qquad -P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\qquad -P\{min(Z_{2},X^{''}_{5})>t-x,min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x|X_{2:5}=x\}\\&\qquad -P\{min(Z_{2},X^{''}_{5})>t-x,min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\} \\&\qquad -P\{min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x,min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\qquad +P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{5})>t-x,\\&\quad \quad \qquad min(Z_{2}, X^{''}_{3},X^{''}_{4})>t-x|X_{2:5}=x\}\\&\qquad +P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{5})>t-x,\\&\quad \quad \qquad min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\ \end{aligned}$$
$$\begin{aligned}&\qquad +P\{min(Z_{2},X^{''}_{5})>t-x,min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x,\\&\quad \quad \qquad min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\qquad +P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x,\\&\quad \quad \qquad min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\qquad -P\{min(Z_{1},X^{''}_{4})>t-x,min(Z_{2},X^{''}_{5})>t-x,\\&\quad \quad \qquad min(Z_{2},X^{''}_{3},X^{''}_{4})>t-x, min(Z_{1},X^{''}_{3},X^{''}_{5})>t-x|X_{2:5}=x\}\\&\quad =P(Z_{1}>t-x)P(X^{''}_{4}>t-x|X_{2:5}=x)\\&\quad \quad +P(Z_{2}>t-x)P(X^{''}_{5}>t-x|X_{2:5}=x)\\&\qquad +P(Z_{1}>t-x)P(X^{''}_{3}>t-x|X_{2:5}=x)\\&\quad \quad \quad P(X^{''}_{5}>t-x|X_{2:5}=x)+P(Z_{2}>t-x) \\ \end{aligned}$$
$$\begin{aligned}&\quad P(X^{''}_{3}>t-x|X_{2:5}=x)P(X^{''}_{4}>t-x|X_{2:5}=x)\\&\quad \quad -P(Z_{1}>t-x)P(Z_{2}>t-x) \\&\quad P(X^{''}_{3}>t-x|X_{2:5}=x)P(X^{''}_{5}>t-x|X_{2:5}=x)\\&\quad \quad -P(Z_{1}>t-x)P(Z_{2}>t-x) \\&\quad P(X^{''}_{3}>t-x|X_{2:5}=x) P(X^{''}_{4}>t-x|X_{2:5}=x)\\&\quad \quad -P(Z_{1}>t-x)P(Z_{2}>t-x) \\&\quad P(X^{''}_{4}>t-x|X_{2:5}=x)P(X^{''}_{5}>t-x|X_{2:5}=x)\\&\quad \quad -P(Z_{1}>t-x)P(X^{''}_{3}>t-x|X_{2:5}=x) \\&\quad P(X^{''}_{4}>t-x|X_{2:5}=x)P(X^{''}_{5}>t-x|X_{2:5}=x)\\&\quad \quad - P(Z_{2}>t-x)P(X^{''}_{3}>t-x|X_{2:5}=x) \\&\quad P(X^{''}_{4}>t-x|X_{2:5}=x)P(X^{''}_{5}>t-x|X_{2:5}=x) \\&\quad \quad + 2P(Z_{1}>t-x)P(Z_{2}>t-x) \\&\quad P(X^{''}_{3}>t-x|X_{2:5}=x) P(X^{''}_{4}>t-x|X_{2:5}=x)P(X^{''}_{5}>t-x|X_{2:5}=x) \\&\quad ={\overline{G}}(t-x)\frac{{\overline{F}}(t)}{{\overline{F}}(x)}+{\overline{H}}(t-x)\frac{{\overline{F}}(t)}{{\overline{F}}(x)}+{\overline{G}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{2}+{\overline{H}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{2}\\&\qquad -{\overline{H}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{3} -{\overline{G}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{3}-3{\overline{H}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{2}{\overline{G}}(t-x) \\&\qquad +2{\overline{H}}(t-x)\left( \frac{{\overline{F}}(t)}{{\overline{F}}(x)}\right) ^{3}{\overline{G}}(t-x). \end{aligned}$$

\(\square \)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roy, A., Gupta, N. Reliability of a coherent system equipped with two cold standby components. Metrika 83, 677–697 (2020). https://doi.org/10.1007/s00184-019-00752-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00184-019-00752-3

Keywords

Search

Navigation