Estimation for varying coefficient panel data model with cross-sectional dependence

Abstract

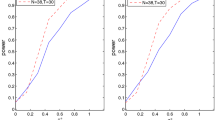
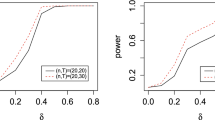
This paper describes a method for estimation and inference with a nonparametric varying coefficients panel data model that allows for cross-sectional dependence and heteroscedasticity, wherein the time series length T is larger than the cross-sectional size N. We first eliminate fixed effects by taking the cross-sectional average, and then use a local linear approach to obtain the initial estimator of the unknown coefficient functions. However, the initial estimator ignores the cross-sectional dependence and heteroscedasticity, which will lead to a loss of efficiency. Thus, we propose a weighted local linear method to obtain a more efficient estimator. In the theoretical part of the paper, we derive the asymptotic theory of the resulting estimator. Simulation results and a real data analysis are provided to illustrate the finite sample performance of the proposed method.

Appendix

Note that Theorems 1–2 follow immediately from Cai et al. (2000) and Theorem 6 follows immediately from Fan et al. (2001), so we omit the proof details here.

Proof of Theorem 3

${\widetilde{w}}_{ij}(z)-w_{ij}(z)$ can be written as

$$\begin{aligned} {\widetilde{w}}_{ij}(z)-w_{ij}(z)=\frac{\sum \nolimits _{t=1}^TK^{\star }_a (z_t-z)\{{\widehat{U}}_{it}{\widehat{U}}_{jt}-w_{ij}(z)\}}{\sum \nolimits _{t=1}^TK^{\star }_a(z_t-z)}=:R_{ij}^{(1)}+R_{ij}^{(2)}, \end{aligned}$$

with

$$\begin{aligned} R_{ij}^{(1)}= & {} \frac{\sum \nolimits _{t=1}^TK^{\star }_a(z_t-z) \{U_{it}U_{jt}-w_{ij}(z)\}}{\sum \nolimits _{t=1}^TK^{\star }_a(z_t-z)},\\ R_{ij}^{(2)}= & {} \frac{\sum \nolimits _{t=1}^TK^{\star }_a(z_t-z) \{{\widehat{U}}_{it}{\widehat{U}}_{jt}-U_{it}U_{jt}\}}{\sum \nolimits _{t=1}^TK^{\star }_a(z_t-z)}. \end{aligned}$$

We can regard $R_{ij}^{(1)}$ as the estimation error of the usual local constant estimator of the conditional expectation $E(U_{it}U_{jt}|z_t=z)$. Under the assumptions given in this paper and the results of the local constant estimator, it can be shown that $|R_{ij}^{(1)}|=O_p(a^2+\frac{1}{\sqrt{Ta}})$ under Assumptions 1–4. Next, we prove the bound of $R_{ij}^{(2)}$. Denote $d_{it}: =\varvec{X}_{it}^{\tau }[\varvec{m}(z_t)-\widehat{\varvec{m}}(z_t)]$, $e_i: =\frac{1}{T}\sum \nolimits _{s=1 }^T\varvec{X}_{is}^{\tau }[\varvec{m}(z_s)-\widehat{\varvec{m}}(z_s)]$ and $f_i: =\frac{1}{T}\sum \nolimits _{s=1 }^TU_{is}$. From (22), ${\widehat{U}}_{it}$ can be expressed as follows

$$\begin{aligned} \begin{aligned}&U_{it}+\varvec{X}_{it}^{\tau }[\varvec{m}(z_t)-\widehat{\varvec{m}}(z_t)]-\frac{1}{T-1}\sum \limits _{s\ne t}^T\varvec{X}_{is}^{\tau }[\varvec{m}(z_s)-\widehat{\varvec{m}}(z_s)] -\frac{1}{T-1}\sum \limits _{s\ne t}^TU_{is}\\&\quad =\frac{T}{T-1}\left\{ U_{it}+\varvec{X}_{it}^{\tau }[\varvec{m}(z_t)-\widehat{\varvec{m}}(z_t)]-\frac{1}{T}\sum \limits _{s=1 }^T\varvec{X}_{is}^{\tau }[\varvec{m}(z_s)-\widehat{\varvec{m}}(z_s)]-\frac{1}{T}\sum \limits _{s=1 }^TU_{is}\right\} \\&\quad = U_{it}+\varvec{X}_{it}^{\tau }[\varvec{m}(z_t)-\widehat{\varvec{m}}(z_t)]-\frac{1}{T}\sum \limits _{s=1}^T\varvec{X}_{is}^{\tau }[\varvec{m}(z_s)-\widehat{\varvec{m}}(z_s)]-\frac{1}{T}\sum \limits _{s=1}^T U_{is}\\&\quad =U_{it}+d_{it}-e_i-f_i, \end{aligned} \end{aligned}$$

where using this equality, we can decompose

$$\begin{aligned} \begin{aligned}&{\widehat{U}}_{it}{\widehat{U}}_{jt}-U_{it}U_{jt}=(-U_{it}e_j-U_{it}f_j-U_{jt}e_i-U_{jt}f_i+e_ie_j+f_if_j+e_if_j+e_jf_i)\\&\quad \quad +(U_{it}d_{jt}+U_{jt}d_{it}+d_{it}d_{jt}-d_{it}e_j-d_{jt}e_i-d_{it}f_j-d_{jt}f_i)\\&\quad \overset{\varDelta }{=}I+II. \end{aligned} \end{aligned}$$

(30)

We let $K^{\star }_t:=K^{\star }_a(z_t-z)$ for brevity. Thus, $R_{ij}^{(2)}$ can be expressed as

$$\begin{aligned} R_{ij}^{(2)}=\frac{1}{{\widehat{f}}(z)}\frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_s(I+II), \end{aligned}$$

(31)

where ${\widehat{f}}(z)$ is a nonparametric kernel estimator of f(z):

$$\begin{aligned} {\widehat{f}}(z)=\frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_s. \end{aligned}$$

Under the assumptions stated in this paper, Lee and Robinson (2015) proved that ${\widehat{f}}(z)$ is consistent. Therefore,

$$\begin{aligned} \frac{1}{{\widehat{f}}(z)}=\frac{1}{f(z)+o_p(1)}=O_p(1). \end{aligned}$$

(32)

Now, we need only find the upper bound of

$$\begin{aligned} \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_s(I+II). \end{aligned}$$

Firstly, we prove the bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sI$.

• 1. As the $U_{it}$ are weakly dependent across time and Assumption 3 implies that $w_{ii},w_{ij}$ are bounded, we have

  $$\begin{aligned} f_i=O_p\left( \frac{1}{\sqrt{T}}\right) . \end{aligned}$$

  (33)

  Additionally, the weak dependence among $(\varvec{X}_{it},z_t)$ and Theorem 1 lead to the following result:

  $$\begin{aligned} e_i=O_p\left( \frac{h^2}{T}+\frac{1}{T\sqrt{h}}\right) . \end{aligned}$$

  (34)

• 2. Because $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sU_{is}$ is the consistent estimator of $E(U_{it}|z_t=z)=0$ with zero bias, we have that

  $$\begin{aligned} \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sU_{is}=O_p \left( \frac{1}{\sqrt{Ta}}\right) . \end{aligned}$$

  (35)

Secondly, we analyze the bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sII$.

• 1. For the first term $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sd_{is}$, we get

  $$\begin{aligned} E\left\{ \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sd_{is}\right\} =E\left\{ E\left\{ \frac{1}{a}K^{\star }_sd_{is}|z_s\right\} \right\} =O(h^2) \end{aligned}$$

  and

  $$\begin{aligned} E\left\{ \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sd_{is}\right\} ^2 =\frac{1}{Ta^2}E\left\{ E\left\{ K^{\star 2}_sd_{is}^2|z_s\right\} \right\} =O\left( \frac{1}{Ta}\left( h^4+\frac{1}{Th}\right) \right) . \end{aligned}$$

  Therefore, the upper bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sd_{is}$ is

  $$\begin{aligned} \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sd_{is}=O_p \left( h^2+\frac{1}{\sqrt{T^2ha}}\right) . \end{aligned}$$

  (36)

• 2. Similar to the proof of (36), we have that

  $$\begin{aligned} E\left\{ \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sU_{is}d_{is}\right\} =E\left\{ \frac{1}{a}K^{\star }_sU_{is}d_{is}\right\} =E\left\{ E\left\{ \frac{1}{a}K^{\star }_sU_{is}d_{is}|z_s\right\} \right\} =0. \end{aligned}$$

  and

  $$\begin{aligned} E\left\{ \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sU_{is}d_{is}\right\} ^2 =\frac{1}{Ta}E\left\{ E\left\{ \frac{1}{a}K^{\star 2}_sU_{is}^2d_{is}^2|z_s\right\} \right\} =O\left( \frac{1}{Ta}\left( h^4+\frac{1}{Th}\right) \right) . \end{aligned}$$

  Then, the upper bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sU_{is}d_{is}$ is

  $$\begin{aligned} \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sU_{is}d_{is} =O_p\left( \frac{h^2}{\sqrt{Ta}}+\frac{1}{\sqrt{T^2ha}}\right) . \end{aligned}$$

  (37)

• 3. Next, we derive the bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sd_{is}d_{js}$. Similar to the proof of (37), we have that the bound of $\frac{1}{Ta}\sum \nolimits _{s=1}^TK^{\star }_sd_{is}d_{js}$ is

  $$\begin{aligned} \frac{1}{Ta}\sum \limits _{s=1}^TK^{\star }_sd_{is}d_{js}=O_p \left( \frac{1}{Th}+h^4\right) . \end{aligned}$$

  (38)

Combining (36)–(38), we conclude that

$$\begin{aligned} R_{ij}^{(2)}=O_p\left( h^2++\frac{1}{Th}+\frac{1}{\sqrt{T^2ha}}\right) , \end{aligned}$$

and $R_{ij}^{(1)}=O_p\Big (a^2+\frac{1}{\sqrt{Ta}}\Big )$. According to Assumption 6, the following equation holds:

$$\begin{aligned} R_{T,a,h}=a^2+\frac{1}{Th}. \end{aligned}$$

Proof of Theorem 4

We only provide the proof for $\frac{h_j^{\star }}{{\widehat{h}}_j^{\star }}\overset{P}{\rightarrow }1$, as the proof for $\frac{{\widetilde{h}}_j^{\star }}{\widehat{{\widetilde{h}}}_j^{\star }}\overset{P}{\rightarrow }1$ follows by the same argument.

$$\begin{aligned} \begin{aligned} h_j^{\star }-{\widehat{h}}_j^{\star }&=\left( \frac{\nu _0}{\mu _2^4T}\right) ^{\frac{1}{5}} \left( \left\{ \frac{\varvec{e}_{j,p}^{\tau }\varvec{1}_N^{T}\varvec{\varSigma }(z) \varvec{1}_N\left( \varvec{V}\varvec{\varOmega }(z)\varvec{V}^{\tau }\right) ^{-1}\varvec{e}_{j,p}}{f(z) (\varvec{m}_j''(z))^2}\right\} ^{\frac{1}{5}}\right. \\&\qquad \left. - \left\{ \frac{\varvec{e}_{j,p}^{\tau }\varvec{1}_N^{T} \widetilde{\varvec{\varSigma }}(z)\varvec{1}_N (\varvec{V}\varvec{\varOmega }(z)\varvec{V}^{\tau })^{-1}\varvec{e}_{j,p}}{{\widehat{f}}(z)(\widehat{\varvec{m}}_j''(z))^2}\right\} ^{\frac{1}{5}}\right) . \end{aligned} \end{aligned}$$

(39)

Let

$$\begin{aligned} \theta _j= & {} \varvec{e}_{j,p}^{\tau }\varvec{1}_N^{T}\varvec{\varSigma }(z)\varvec{1}_N(\varvec{V}\varvec{\varOmega }(z)\varvec{V}^{\tau })^{-1}\varvec{e}_{j,p},\\ {\widehat{\theta }}_j= & {} \varvec{e}_{j,p}^{\tau }\varvec{1}_N^{T}\widetilde{\varvec{\varSigma }}(z)\varvec{1}_N(\varvec{V}\varvec{\varOmega }(z)\varvec{V}^{\tau })^{-1}\varvec{e}_{j,p}. \end{aligned}$$

By the mean value theorem, the second term in (39) is bounded in absolute value by

$$\begin{aligned} |{\widetilde{r}}_1\Vert |\theta _j-{\widehat{\theta }}_j|+|{\widetilde{r}}_2\Vert f(z)-{\widehat{f}}(z)|+|{\widetilde{r}}_3\Vert \varvec{m}_j''(z)-\widehat{\varvec{m}}_j''(z)|, \end{aligned}$$

(40)

where $r_i,i=1,2,3$ are derivatives of the expression of $\{\frac{\theta _j}{f(z)(\varvec{m}_j''(z))^2}\}^{\frac{1}{5}}$ with respect to $\theta _j,f,(m_j'')^2$.

${\widetilde{r}}_1$ lies in

$$\begin{aligned} \frac{1}{5}\left[ \left( \frac{1}{f(z)(\varvec{m}_j''(z))^2}\right) ^{\frac{1}{5}}\theta _j^{-\frac{4}{5}}, \left( \frac{1}{{\widehat{f}}(z)(\widehat{\varvec{m}}_j''(z))^2}\right) ^{\frac{1}{5}}{\widehat{\theta }}_j^{-\frac{4}{5}}\right] , \end{aligned}$$

${\widetilde{r}}_2$ lies in

$$\begin{aligned} -\frac{1}{5}\left[ \left( \frac{\theta _j}{(\varvec{m}_j''(z))^2}\right) ^ {\frac{1}{5}}f(z)^{-\frac{6}{5}}, \left( \frac{{\widehat{\theta }}_j}{(\widehat{\varvec{m}}_j''(z))^2}\right) ^{\frac{1}{5}}{\widehat{f}}(z)^{-\frac{6}{5}}\right] , \end{aligned}$$

and ${\widetilde{r}}_3$ lies in

$$\begin{aligned} -\frac{1}{5}\left[ \left( \frac{\theta _j}{f(z)}\right) ^{\frac{1}{5}}((\varvec{m}_j''(z))^2)^{-\frac{6}{5}}, \left( \frac{{\widehat{\theta }}_j}{{\widehat{f}}(z)}\right) ^{\frac{1}{5}}\left( (\widehat{\varvec{m}}_j''(z))^2\right) ^{-\frac{6}{5}}\right] . \end{aligned}$$

Hence, we deduce the upper bound of (40) as

$$\begin{aligned}&O_p\left\{ \theta _j^{-\frac{4}{5}} \left[ |\theta _j-{\widehat{\theta }}_j|+\theta _j|f(z) -{\widehat{f}}(z)|+\theta _j|(\varvec{m}_j''(z))^2-(\widehat{\varvec{m}}_j''(z))^2|\right] \right\} \\&\quad =O_p\left\{ \theta _j^{-\frac{4}{5}} N[\Vert \varvec{\varSigma }(z)-\widetilde{\varvec{\varSigma }}(z)\Vert +\Vert \varvec{\varSigma }(z)\Vert |f(z)-{\widehat{f}}(z)|+\Vert \varvec{\varSigma }(z)\Vert | (\varvec{m}_j''(z))^2-(\widehat{\varvec{m}}_j''(z))^2|\right\} \\&\quad =O_p\left\{ \theta _j^{-\frac{4}{5}}N\Vert \varvec{\varSigma }(z)-\widetilde{\varvec{\varSigma }}(z)\Vert \right\} , \end{aligned}$$

where the last step follows from Assumption 7. Thus, (39) becomes

$$\begin{aligned} h_j^{\star }-{\widehat{h}}_j^{\star }&=O_p\left\{ \left( \frac{\theta _j}{T}\right) ^{\frac{1}{5}}\frac{N}{\theta _j}\Vert \varvec{\varSigma }(z)-\widetilde{\varvec{\varSigma }}(z)\Vert \right\} \\&=O_p\left\{ \left( \frac{\theta _j}{T}\right) ^ {\frac{1}{5}}\Vert \varvec{\varSigma }(z)-\widetilde{\varvec{\varSigma }}(z)\Vert \right\} \\&=o_p\left( \left( \frac{\theta _j}{T}\right) ^{\frac{1}{5}}\right) \\&=o_p(h_j^{\star }). \end{aligned}$$

Proof of Theorem 5

First, we denote $\varvec{A}=\varvec{I}_T\otimes \varvec{1}_N^{\tau }$, $\varvec{Y}= (\varvec{Y}_{.1},\ldots ,\varvec{Y}_{.T})$, $\varvec{Xz}=(\varvec{Xz}^{\tau }_1,\ldots ,\varvec{Xz}^{\tau }_T)^{\tau }$ with the blocks $\varvec{Xz}_t =(\varvec{X}_{.t}, \varvec{X}_{.t}(z_t-z))$, $\varvec{B}$ and $\widetilde{\varvec{B}}$ are both block diagonal matrices with the blocks $\varvec{\varSigma }^{-\frac{1}{2}}(\varvec{z}_t)$ and $\widetilde{\varvec{\varSigma }}^{-\frac{1}{2}}(\varvec{z}_t)$ respectively. Thus, we can express $\varvec{Y}_{\varvec{\varSigma }}$ and $\varvec{Y}_{\widetilde{\varvec{\varSigma }}}$ as

$$\begin{aligned} \begin{aligned}&\varvec{Y}_{\varvec{\varSigma }}=\frac{1}{N}\varvec{A}\varvec{B}{\text {Vec}}(\varvec{Y}),\qquad \varvec{D}_{\varvec{\varSigma }}(z)=\frac{1}{N}\varvec{A}\varvec{B}\varvec{Xz} ,\\&\varvec{Y}_{\widetilde{\varvec{\varSigma }}}=\frac{1}{N}\varvec{A}\varvec{{\widetilde{B}}}{\text {Vec}}(\varvec{}Y),\qquad \varvec{D}_{\widetilde{\varvec{\varSigma }}}(z)=\frac{1}{N}\varvec{A}\varvec{{\widetilde{B}}}\varvec{Xz}, \end{aligned} \end{aligned}$$

which leads to

$$\begin{aligned} \begin{aligned} \widetilde{\varvec{m}}(z)&=(\varvec{I}_p,\varvec{O}_p)[\varvec{X}_z\varvec{B}\varvec{A}^{\tau }\varvec{W}(z)AB\varvec{X}_z]^{-1}[\varvec{Xz}\varvec{B}\varvec{A}^{\tau }\varvec{W}(z)\varvec{A}\varvec{B}{\text {Vec}}(\varvec{Y})], \\ \widetilde{\varvec{m}}^{*}(z)&=(\varvec{I}_p,\varvec{O}_p)[\varvec{X}_z\varvec{{\widetilde{B}}}\varvec{A}^{\tau }\varvec{W}(z)\varvec{A}\varvec{{\widetilde{B}}}\varvec{X}_z]^{-1}[\varvec{Xz}\varvec{{\widetilde{B}}}\varvec{A}^{\tau }\varvec{W}(z)\varvec{A}\varvec{{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]. \end{aligned} \end{aligned}$$

Next, we decompose $\widetilde{\varvec{m}}(z)-\widetilde{\varvec{m}}^{\star }(z)$ as follows

$$\begin{aligned} \begin{aligned} \widetilde{\varvec{m}}(z)-\widetilde{\varvec{m}}^{\star }(z)&=(\varvec{I}_p,\varvec{O}_p)\left\{ [\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}[\varvec{Xz}BA^{\tau }\varvec{W}(z)\varvec{AB}{\text {Vec}}(\varvec{Y})]\right. \\&\qquad \left. -[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}\varvec{Xz}]^{-1}[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]\right\} \\&=(\varvec{I}_p,\varvec{O}_p)\left\{ [\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}[\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}{\text {Vec}}(\varvec{Y})]\right. \\&\qquad -[\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]\\&\qquad +[\varvec{Xz}BA^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]\\&\qquad \left. -[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}\varvec{Xz}]^{-1}[\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]\right\} \\&=(\varvec{I}_p,\varvec{O}_p)\left\{ [\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}\right. \\&\qquad \times [\varvec{Xz}(\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}-\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}){\text {Vec}}(\varvec{Y})]\\&\qquad +([\varvec{Xz}BA^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1}-[\varvec{Xz}\varvec{BA}^{\tau }\varvec{W}(z)\varvec{AB}\varvec{Xz}]^{-1})\\&\qquad \times \left. [\varvec{Xz}\varvec{{\widetilde{B}}A}^{\tau }\varvec{W}(z)\varvec{A{\widetilde{B}}}{\text {Vec}}(\varvec{Y})]\right\} . \end{aligned} \end{aligned}$$

The bound for the every part in the last step is

$$\begin{aligned} \begin{aligned}&[\varvec{Xz}(BA^{\tau }\varvec{W}(z)AB-{\widetilde{B}}A^{\tau }\varvec{W}(z)A{\widetilde{B}}){\text {Vec}}(\varvec{Y})]\\&\quad =O_p(\Vert B-{\widetilde{B}}\Vert \Vert B\Vert \Vert A^{\tau }\varvec{W}(z)A\Vert ),\\&\quad \quad \times [\varvec{Xz}BA^{\tau }\varvec{W}(z)AB\varvec{Xz}]\\&\quad =O_p(\Vert B\Vert ^2\Vert A^{\tau }\varvec{W}(z)A\Vert ),\\&\quad \quad \times [\varvec{Xz}BA^{\tau }\varvec{W}(z)AB{\text {Vec}}(\varvec{Y})]\\&\quad =O_p(\Vert B\Vert ^2\Vert A^{\tau }\varvec{W}(z)A\Vert ),\\&\quad \quad \times [\varvec{Xz}BA^{\tau }\varvec{W}(z)AB\varvec{Xz}]^{-1}-[\varvec{Xz}BA^{\tau }\varvec{W}(z)AB\varvec{Xz}]^{-1}\\&\quad =[\varvec{Xz}BA^{\tau }\varvec{W}(z)AB\varvec{Xz}]^{-1}([\varvec{Xz}{\widetilde{B}}A^{\tau }\varvec{W}(z)A{\widetilde{B}}\varvec{Xz}]\\&\quad \quad -[\varvec{Xz}BA^{\tau }\varvec{W}(z)AB\varvec{Xz}])[\varvec{Xz}{\widetilde{B}}A^{\tau }\varvec{W}(z)A{\widetilde{B}}\varvec{Xz}]^{-1}. \end{aligned} \end{aligned}$$

Hence, $\widetilde{\varvec{m}}(z)-\widetilde{\varvec{m}}^{\star }(z)$ is bounded by

$$\begin{aligned} \widetilde{\varvec{m}}(z)-\widetilde{\varvec{m}}^{\star }(z)=O_p \left( \frac{\Vert \varvec{B}-\varvec{{\widetilde{B}}}\Vert }{\Vert \varvec{B}\Vert }\right) . \end{aligned}$$

According to the mean value theorem, $\Vert \varvec{B}-\varvec{{\widetilde{B}}}\Vert$ is bounded by $|l\Vert |\varvec{B}^{-2}-\varvec{{\widetilde{B}}}^{-2}\Vert$, and l lies in $[-\frac{1}{2}B^3,-\frac{1}{2}\varvec{{\widetilde{B}}}^3]$, so

$$\begin{aligned} \Vert \varvec{B}^{-2}-\varvec{{\widetilde{B}}}^{-2}\Vert =O_p(NTR_{T,a,h}). \end{aligned}$$

Thus,

$$\begin{aligned} \Vert \varvec{B}-\varvec{{\widetilde{B}}}\Vert =O_p(NTR_{T,a,h}). \end{aligned}$$

Combined with

$$\begin{aligned} \Vert \varvec{B}\Vert =T\Vert \varvec{\varSigma }^{-\frac{1}{2}}\Vert , \end{aligned}$$

we have that

$$\begin{aligned} \widetilde{\varvec{m}}(z)-\widetilde{\varvec{m}}^{\star }(z)=O_p \left( \frac{\Vert \varvec{B}-\varvec{{\widetilde{B}}}\Vert }{\Vert \varvec{B}\Vert } \right) =O_p(\Vert \varvec{\varSigma }^{-\frac{1}{2}}\Vert ^{-1}NR_{T,a,h}). \end{aligned}$$

Because $N(Th)^{-1}=o(N^{-\frac{1}{2}}(Th)^{-\frac{1}{2}})=o((Th)^{-\frac{1}{2}})$, which is implied by $N^3/(Th)\rightarrow 0$, Assumption 6-(b) implies that $NR_{T,a,h}=o(\frac{1}{\sqrt{Th}}+h^2)$.