Likelihood ratio confidence interval for the abundance under binomial detectability models

Abstract

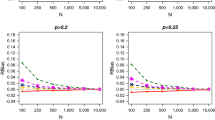
Binomial detectability models are often used to estimate the size or abundance of a finite population in biology, epidemiology, demography and reliability. Special cases include incompletely observed multinomial models, capture–recapture models, and distance sampling models. The most commonly-used confidence interval for the abundance is the Wald-type confidence interval, which is based on the asymptotic normality of a reasonable point estimator of the abundance. However, the Wald-type confidence interval may have poor coverage accuracy and its lower limit may be less than the number of observations. In this paper, we rigorously establish that the likelihood ratio test statistic for the abundance under the binomial detectability models follows the chisquare limiting distribution with one degree of freedom. This provides a solid theoretical justification for the use of the proposed likelihood ratio confidence interval. Our simulations indicate that in comparison to the Wald-type confidence interval, the likelihood ratio confidence interval not only has more accurate coverage rate, but also exhibits more stable performance in a variety of binomial detectability models. The proposed interval is further illustrated through analyzing three real data-sets.

Appendix

1.1 A. Regularity conditions on $k(x;\theta )$

We assume that $k(x;\theta )$ satisfies the following regularity conditions, which are from §4.2.2 of Serfling (1980).

(R1):

Let $\varTheta$ be the parameter space of $\theta$ and $\theta _0$ be its true value. Suppose $\varTheta$ is an open set and $\theta _0$ belongs to $\varTheta$.

(R2):

For each $\theta \in \varTheta$, the derivatives

$$\begin{aligned} \frac{\partial \log k(x; \theta )}{\partial \theta }, \; \frac{\partial ^2 \log k(x; \theta )}{\partial \theta ^2},\; \frac{\partial ^3 \log k(x; \theta )}{\partial \theta ^3} \end{aligned}$$

exist for all x.

(R3):

There exist functions g(x), h(x) and H(x) such that for $\theta$ in a neighborhood of $\theta _0$,

$$\begin{aligned} \Big | \frac{\partial \log k(x; \theta )}{\partial \theta } \Big | \le g(x), \; \Big | \frac{\partial ^2 \log k(x; \theta )}{\partial \theta ^2} \Big | \le h(x), \; \Big | \frac{\partial ^3 \log k(x; \theta )}{\partial \theta ^3} \Big | \le H(x) \end{aligned}$$

hold for all x and

$$\begin{aligned} \int g(x) dx<\infty , \; \int h(x) dx<\infty , \; \int H(x) k(x; \theta )dx <\infty . \end{aligned}$$

(R4):

For each $\theta \in \varTheta$, $0< \int \left\{ \partial \log k(x; \theta )/\partial \theta \right\} ^2 k(x; \theta )dx <\infty$.

1.2 B. Technical preparations

We make technical preparations for the proof of Theorem 1. For any positive real number x greater than n, define the digamma function $\psi _0(x) = d \log \{ \varGamma (x)\}/dx$ and $S_1(x, n) = \psi _0(x+1) - \psi _0(x-n+1).$ For $a=1,2,\dots$, we define the polygamma functions

$$\begin{aligned} \psi _a(x) =&\frac{d^{a+1}\log \{ \varGamma (x)\} }{dx^{a+1} } = \frac{d^{a}\psi _0(x) }{dx^{a} } =(-1)^{a+1}a!\sum _{k=0}^{\infty } \frac{1}{(x+k)^{a+1}}, \end{aligned}$$

(6)

$$\begin{aligned} S_{a}(x, u) =&\psi _{a-1}(x+1) - \psi _{a-1}(x-u+1) =(-1)^{a-1}(a-1)!\sum _{k=x-u+1}^{x} k^{-a}.\nonumber \\ \end{aligned}$$

(7)

It is clear that $\psi _1(x) = d\psi _0(x)/dx$ and therefore $S_{2}(x, n) = d S_{1}(x, n)/dx.$

Since $x^{-1}$ and $x^{-2}$ are both monotone decreasing functions for $x>0$, it follows from Eqs. (6) and (7) that

$$\begin{aligned}&\log \{ (N+1)/(N+1-n)\}<S_1(N,n)<\log \{ N/(N-n) \}, \\&-n/\{N(N-n)\}<S_2(N,n)< -n/\{ (N+1)(N+1-n)\}. \end{aligned}$$

Note that the number n of detected observations follows a binomial distribution $B(N_0,p(\theta _0))$. By the central limit theorem,

$$\begin{aligned} \sqrt{N_0}\left\{ \frac{n}{N_0}-p(\theta _0) \right\} {\overset{d}{\longrightarrow \; }}\; N\left( 0, \; p(\theta _0) \{1-p(\theta _0) \}\right) , \end{aligned}$$

as $N_0 \rightarrow \infty$. Therefore, it follows that

$$\begin{aligned} S_1(N_0,n) =&\log \{ N_0/\left( N_0-n\right) \} + O_p\left( N_0^{-1}\right) \\ =&- \log \{1-p(\theta _0)\} + \frac{\left( n/N_0\right) -p\left( \theta _0\right) }{ 1-p\left( \theta _0\right) } + O_p\left( N_0^{-1}\right) , \\ S_2\left( N_0,n\right) =&- \frac{n}{N_0\left( N_0-n\right) }+ O_p\left( N_0^{-2}\right) \\ =&- \frac{p\left( \theta _0\right) }{N_0\{ 1-p(\theta _0) \}}+ O_p\left( N_0^{-3/2}\right) . \end{aligned}$$

The following lemma from Hjort and Pollard (2011) can ease much of the technical burden in our proof of Theorem 1.

Lemma 2

Assume that $\theta ^{{\mathrm {\scriptscriptstyle \top }}}=(\theta _{1}^{{\mathrm {\scriptscriptstyle \top }}}, \theta _{2}^{{\mathrm {\scriptscriptstyle \top }}})$ where $\theta _1$ and $\theta _2$ are r- and s-dimensional vectors, respectively. Let $\theta _0^{{\mathrm {\scriptscriptstyle \top }}}=(\theta _{10}^{{\mathrm {\scriptscriptstyle \top }}}, \theta _{20}^{{\mathrm {\scriptscriptstyle \top }}})$ be its true value, and $\gamma =(\gamma _{1}^{{\mathrm {\scriptscriptstyle \top }}}, \gamma _{2}^{{\mathrm {\scriptscriptstyle \top }}})^{{\mathrm {\scriptscriptstyle \top }}} = \sqrt{n}(\theta -\theta _0)$ where n is the sample size. Suppose for $\theta = \theta _0+O_p(n^{-1/2})$, it holds that

$$\begin{aligned} H(\theta ) = C_n + a_n^{{\mathrm {\scriptscriptstyle \top }}} \gamma - \frac{1}{2} \gamma ^{{\mathrm {\scriptscriptstyle \top }}}A\gamma + \varepsilon _n(\theta ) \end{aligned}$$

where $a_n=O_p(1)$, A is a positive definite matrix, $C_n$ does not depend on $\theta$, and $\varepsilon _n(\theta )= o_p(1)$ for any fixed $\theta$. According to $\theta =(\theta _{1}^{{\mathrm {\scriptscriptstyle \top }}}, \theta _{2}^{{\mathrm {\scriptscriptstyle \top }}})^{{\mathrm {\scriptscriptstyle \top }}}$, we partition A into $A = (A_{ij})_{1\le i, j\le 2}$, and partition $a_n^{{\mathrm {\scriptscriptstyle \top }}}$ into $(a_{n1}^{{\mathrm {\scriptscriptstyle \top }}}, a_{n2}^{{\mathrm {\scriptscriptstyle \top }}})$. As $n\rightarrow \infty$, if $a_n{\overset{d}{\longrightarrow \; }}N(0, A)$, then

• (a) the maximizer $\hat{\theta }$ of $H(\theta )$ satisfies $\sqrt{n}(\hat{\theta }-\theta _0) = A^{-1}a_n + o_p(1) {\overset{d}{\longrightarrow \; }}N(0, A^{-1})$,

• (b) $2\{ \mathop {\max }\nolimits _{\theta } H(\theta ) - H(\theta _0) \} = a_n^{{\mathrm {\scriptscriptstyle \top }}} A^{-1} a_n + o_p(1) {\overset{d}{\longrightarrow \; }}\chi _{r+s}^2$, and

• (c) $2\{ \mathop {\max }\nolimits _{\theta } H(\theta )- \mathop {\max }\nolimits _{\theta _2} H(\theta _{10}, \theta _2)\} = a_n^{{\mathrm {\scriptscriptstyle \top }}} A^{-1} a_n - a_{n2}^{{\mathrm {\scriptscriptstyle \top }}} A_{22}^{-1} a_{n2}+o_p(1) {\overset{d}{\longrightarrow \; }}\chi _{r}^2$.

1.3 C. Proof of Theorem 1

Using a similar argument to that in the proofs of Lemma 1 and Theorem 1 of Qin and Lawless (1994), we have $\hat{N} = N_0 +O_p(N_0^{1/2})$ and $\hat{\theta } - \theta _0 = O_p(N_0^{-1/2})$. Since the results in Theorem 1 are about the properties of $( \hat{N}, \hat{\theta })$, our proof begins by studying the behavior of $\ell (N, \theta )$ for $(N, \theta )$ such that $( (N-N_0)/N_0, \theta -\theta _0) = O_p(N_0^{-1/2})$.

Let $\alpha =(\alpha _1, \alpha _2^{{\mathrm {\scriptscriptstyle \top }}})^{{\mathrm {\scriptscriptstyle \top }}}$ with $\alpha _1 =N_0^{-1/2}(N-N_0)$ and $\alpha _2 = N_0^{1/2}(\theta -\theta _0)$. Define $H(\alpha ) = \ell ( N_0 +N_0^{1/2} \alpha _1, \theta _0+N_0^{-1/2}\alpha _2)$. The likelihood ratio function of $(N, \theta )$ can be expressed as

$$\begin{aligned} R(N, \theta ) = 2\{ H(\alpha ) - H(0) \}. \end{aligned}$$

By the second-order Taylor expansion, we have

$$\begin{aligned} H(\alpha ) = H(0) + \alpha ^{\mathrm {\scriptscriptstyle \top }}u + \frac{1}{2} \alpha ^{{\mathrm {\scriptscriptstyle \top }}} V \alpha + o_p(1), \end{aligned}$$

where $u \equiv (u_1, u_2^{\mathrm {\scriptscriptstyle \top }})^{\mathrm {\scriptscriptstyle \top }}=\partial H(0)/\partial \alpha$ and V is the leading term of $\partial ^2 H(0)/(\partial \alpha \partial \alpha ^{\mathrm {\scriptscriptstyle \top }})$.

To proceed, we need the expressions of u and V. It can be seen that

$$\begin{aligned} \frac{\partial \ell (N, \theta )}{\partial N}&= S_1(N,n) + \log \{1-p(\theta )\},\\ \frac{\partial \ell (N, \theta )}{\partial \theta }&= \frac{n-N p(\theta )}{p(\theta )\{1-p(\theta )\} } \frac{d p(\theta )}{d\theta } + \sum _{i=1}^n \frac{\partial \log \{ k(x_i; \theta )\} }{ \partial \theta }. \end{aligned}$$

According to the properties of the digamma functions, we further have

$$\begin{aligned} u_1&=\frac{\partial H(0)}{\partial \alpha _1}= N_0^{1/2} \frac{\partial \ell (N_0, \theta _0)}{\partial N} \\&=N_0^{1/2} \left[ S_1(N_0,n) + \log \{1-p(\theta _0)\} \right] \\&=N_0^{1/2} \frac{ (n/N_0) -p(\theta _0) }{ 1-p(\theta _0) }+ O_p\left( N_0^{-1/2}\right) . \end{aligned}$$

and

$$\begin{aligned} u_2&= \frac{\partial H(0)}{\partial \alpha _2}= N_0^{-1/2} \frac{\partial \ell (N_0, \theta _0)}{\partial \theta } \\&= N_0^{-1/2} \left[ \frac{n- N_0p(\theta _0)}{ 1-p(\theta _0) } \frac{d \log \{ p(\theta _0)\} }{d\theta } + \sum _{i=1}^n \frac{d \log \{ k(x_i,\theta _0)\} }{ d\theta } \right] \\&=N_0^{1/2} \frac{(n/N_0) - p(\theta _0)}{ 1-p(\theta _0) } p_1(\theta _0) + \{p(\theta _0)\}^{1/2} n^{-1/2} \sum _{i=1}^n \frac{d \log \{ k(x_i,\theta _0)\} }{ d\theta } \\&\quad + O_p\left( N_0^{-1/2}\right) . \end{aligned}$$

By the central limit theorem, it can be shown that $u{\overset{d}{\longrightarrow \; }}N(0, \varSigma )$.

Write $V=(V_{ij})_{1\le i,j\le 2}$. It can be seen that $V_{11}$ is the leading term of

$$\begin{aligned} \frac{\partial H(0)}{\partial \alpha _1^2} = N_0 \frac{\partial \ell (N_0, \theta _0)}{\partial N^2} = N_0 S_2(N_0,n) = - \frac{p(\theta _0)}{1-p(\theta _0)} +O_p\left( N_0^{-1/2}\right) , \end{aligned}$$

where we have used an approximate of $S_2(N_0, n)$. This implies that

$$\begin{aligned} V_{11} = - \frac{p(\theta _0)}{1-p(\theta _0)}. \end{aligned}$$

With tedious algebra, we similarly have

$$\begin{aligned} V_{21} = - \frac{p(\theta _0)}{1-p(\theta _0)} p_1(\theta _0), \quad V_{22} = - \frac{p(\theta _0) }{ 1-p(\theta _0) } p_1(\theta _0) \{p_1(\theta _0) \}^{{\mathrm {\scriptscriptstyle \top }}} - p(\theta _0) I(\theta _0). \end{aligned}$$

Since $u{\overset{d}{\longrightarrow \; }}N(0, \varSigma )$ and $V = -\varSigma$, Theorem 1 is proved by applying Lemma 2. $\square$