Focused vector information criterion model selection and model averaging regression with missing response

Abstract

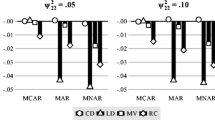
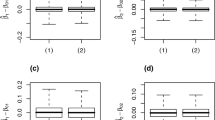
In this paper, a focused vector information criterion for model selection and model averaging is considered for the linear model with missing response. Based on the focused information criterion of Hjort and Claeskens (J Am Stat Assoc 98:879–945, 2003) and imputation idea, a frequentist model averaging estimator for a focused vector of a linear model is proposed, and the estimator is shown to be root-n consistent and asymptotical normal. In addition, the proposed focused vector information criterion is designed for focused multidimensional parameter, which is a little different from conventional focused information criterion for one dimensional focused parameter. A model averaging based confidence interval estimation method and estimation of the mean of the response are also proposed. A simulation study is conducted to investigate the performance of the proposed estimator with finite sample sizes and a real data example is presented to illustrate its application in practice.

Appendix: Proofs

The following Lemma 1 is needed to prove the theorems.

Lemma 1

Under condition C1, we have

$$\begin{aligned} \begin{array}{lll}\displaystyle \sqrt{n}(\tilde{\beta }_n-\beta _0)=\frac{\Sigma _0^{-1}}{\sqrt{n}}\sum \limits _{i=1}^n\delta _iX_i\varepsilon _i+o_p(1). \end{array} \end{aligned}$$

Proof of Lemma 1

It is easily seen that

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\tilde{\beta }_{n}-\beta _0)&= \displaystyle \left( \frac{1}{n}\sum \limits _{i=1}^n\delta _iX_iX_i^\top \right) ^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^n\delta _iX_i\varepsilon _i. \end{array} \end{aligned}$$

Note that

$$\begin{aligned} \frac{1}{n}\sum \limits _{i=1}^n\delta _iX_iX_i^\top \stackrel{P}{\longrightarrow }\Sigma _0. \end{aligned}$$

Lemma 1 then follows Directly.

Proof of Theorem 1

Denote $A_{n}=\frac{1}{n}\sum _{i=1}^{n}\Pi _SX_{i}X_{i}^{\top }\Pi _S^{\top }$, with a simple calculation, we obtain

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\hat{\beta }_{S}-\Pi _S\beta _0)&{}=&{}\displaystyle A_{n}^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\Pi _SX_i\left( \hat{H}_{i}-X_i^{\top }\Pi _S^{\top }\Pi _S\beta _0\right) \\ &{}=&{}\displaystyle \displaystyle A_{n}^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\Pi _SX_i\left( \delta _{i}\varepsilon _i-\delta _{i}X_i^{\top }(\tilde{\beta }_n-\beta _0)\!+\!X_i^{\top }\tilde{\beta }_n-X_i^{\top }\Pi _S^{\top }\Pi _S\beta _0\right) \\ &{}=&{}\displaystyle B_{n1}+B_{n2}+B_{n3}.\end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} B_{n1}&{}=&{}\displaystyle A_{n}^{-1}\Pi _S\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}X_i\varepsilon _i,\\ B_{n2}&{}=&{}\displaystyle \displaystyle A_{n}^{-1}\frac{1}{\sqrt{n}}\Pi _S\sum \limits _{i=1}^{n}(1-\delta _{i})X_iX_i^{\top }(\tilde{\beta }_n-\beta _0),\\ B_{n3}&{}=&{}\displaystyle \displaystyle A_{n}^{-1}\frac{1}{\sqrt{n}}\Pi _S\sum \limits _{i=1}^{n}X_iX_i^{\top }(I-\Pi _S^{\top }\Pi _S)\beta _0. \end{array} \end{aligned}$$

Under Condition C1, it is not difficult to get

$$\begin{aligned} A_{n}\stackrel{P}{\longrightarrow }\Pi _S\Sigma \Pi _S^{\top }. \end{aligned}$$

Thus,with Lemma 1 in hand, we have

$$\begin{aligned} B_{n2}&= \displaystyle A_{n}^{-1}\Pi _S\left( \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X_iX_i^{\top }\right) \sqrt{n}(\tilde{\beta }_n-\beta _0)\\&= \displaystyle A_{n}^{-1}\Pi _S\left( \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X_iX_i^{\top }\right) \frac{\Sigma _0^{-1}}{\sqrt{n}}\sum \limits _{i=1}^n\delta _iX_i\varepsilon _i+o_p(1).\\ B_{n3}&= \displaystyle A_{n}^{-1}\Pi _S\left( \frac{1}{n}\sum \limits _{i=1}^{n}X_iX_i^{\top }\right) (I-\Pi _S^{\top }\Pi _S)\sqrt{n}\beta _0\\&= \displaystyle A_{n}^{-1}\Pi _S\left( \frac{1}{n}\sum \limits _{i=1}^{n}X_iX_i^{\top }\right) (I-\Pi _S^{\top }\Pi _S)\sqrt{n}\left( \begin{array}{c} \ddot{ \beta }_0\\ \eta /\sqrt{n} \end{array} \right) \\&= \displaystyle A_{n}^{-1}\Pi _S\left( \frac{1}{n}\sum \limits _{i=1}^{n}X_iX_i^{\top }\right) (I-\Pi _S^{\top }\Pi _S)\left( \begin{array}{c} 0\\ \eta \end{array} \right) \\&= \displaystyle (\Pi _S\Sigma \Pi _S^{\top })^{-1}\Pi _S\Sigma (I-\Pi _S^{\top }\Pi _S)\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1).\\ \end{aligned}$$

The second last equation follows from $(I-\Pi _S^{\top }\Pi _S)\left( \begin{array}{c} \ddot{ \beta }_0\\ 0 \end{array} \right) =0$. Thus, we have

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\hat{\beta }_{S}-\Pi _S\beta _0)&{}=&{}\displaystyle A_{n}^{-1}\Pi _S\left( \Sigma _0+\left( \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X_iX_i^{\top }\right) \right) \frac{\Sigma _0^{-1}}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}X_i\varepsilon _i\\ &{}&{}\displaystyle +(\Pi _S\Sigma \Pi _S^{\top })^{-1}\Pi _S\Sigma (I-\Pi _S^{\top }\Pi _S)\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1). \end{array} \end{aligned}$$

Note that

$$\begin{aligned} \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X_iX_i^{\top }\stackrel{P}{\longrightarrow }\Sigma -\Sigma _0. \end{aligned}$$

By the central limit theorem and slutsky’ theorem, we have

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\hat{\beta }_{S}-\Pi _S\beta _0)&{}\stackrel{d}{\longrightarrow }&{}\displaystyle (\Pi _S\Sigma \Pi _S^{\top })^{-1}\Pi _S\Sigma \Sigma _0^{-1}G +(\Pi _S\Sigma \Pi _S^{\top })^{-1}\Pi _S\Sigma (I-\Pi _S^{\top }\Pi _S)\left( \begin{array}{c} 0\\ \eta \end{array} \right) . \end{array} \end{aligned}$$

And a slight transformation of the last equation completes the proof of Theorem 1.

Proof of Theorem 2

Theorem 2 is not difficult to arrive by the delta method and Theorem 3 of Van der Vaart and Wellner (1996) based on Theorem 1.

Proof of Theorem 3

It can be verified that

$$\begin{aligned} \sqrt{n} (\hat{\phi }-\phi _0)&= \sum \limits _S w(S|\hat{\eta })\sqrt{n}(\hat{\phi }_S-\phi _0)\\&= \sum \limits _S w(S|\hat{\eta })\left\{ \phi ^{\prime }_{\beta _0}\Pi ^{\top }_S(\Pi _S\Sigma \Pi _S^{\top })^{-1} \Pi _S\Sigma \Sigma ^{-1}_0 G+\phi ^{\prime }_{\beta _0}A_S\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1)\right\} \\&= \sum \limits _S w(S|\hat{\eta }) \phi ^{\prime }_{\beta _0}\Pi ^{\top }_S(\Pi _S\Sigma \Pi _S^{\top })^{-1} \Pi _S\Sigma \Sigma ^{-1}_0 G+\sum \limits _S w(S|\hat{\eta })\phi ^{\prime }_{\beta _0}A_S\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1). \end{aligned}$$

Since $\hat{\eta }\stackrel{d}{\longrightarrow }\Delta$, we have

$$\begin{aligned} w(S|\hat{\eta })\stackrel{d}{\longrightarrow }w(S|\Delta ) \end{aligned}$$

by the continuous mapping theorem, and then Theorem 3 follows directly.

Proof of Theorem 4

It is easily seen that

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\hat{\theta }-\theta )&{}=&{}\displaystyle \frac{1}{\sqrt{n}} \sum \limits _{i=1}^{n}\{\delta _iY_i+(1-\delta _i)X^{\top }_i\hat{\beta }_{sfvic}-\theta \}\\ &{}=&{}\displaystyle \displaystyle \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}\varepsilon _i +\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}(X^{\top }_i\beta _0-\theta )+\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}(1-\delta _{i})X^{\top }_i(\hat{\beta }_{sfvic}-\beta _0)\\ &{}\doteq &{}\displaystyle H_{n1}+H_{n2}+H_{n3}.\\ \end{array} \end{aligned}$$

For $H_{n3}$, we have

$$\begin{aligned} H_{n3}&= \displaystyle \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X^{\top }_i\sqrt{n}(\hat{\beta }_{sfvic}-\beta _0)\nonumber \\&= \displaystyle \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X^{\top }_i\sum \limits _S w(S|\hat{\eta })\sqrt{n}(\Pi ^{\top }_{S}\hat{\beta }_{S}-\beta _0). \end{aligned}$$

(2)

Note that

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\Pi ^{\top }_{S}\hat{\beta }_{S}-\beta _0)&{}=&{}\displaystyle \Pi _S(\Pi _S\Sigma \Pi _S^{\top })^{-1}\Pi _S\Sigma \Sigma _0^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}X_i\varepsilon _i +A_S\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1). \end{array} \nonumber \\ \end{aligned}$$

(3)

Plugging (3) into (2), we have

$$\begin{aligned} \begin{array}{lll} H_{n3} &{}=&{}\displaystyle \frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X^{\top }_i\sum \limits _S w(S|\hat{\eta }) R_S\Sigma \Sigma _0^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}X_i\varepsilon _i\\ &{}&{}\displaystyle +\frac{1}{n}\sum \limits _{i=1}^{n}(1-\delta _{i})X^{\top }_i\sum \limits _S w(S|\hat{\eta })A_S\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1). \end{array} \end{aligned}$$

Since the term $\frac{1}{n}\sum _{i=1}^{n}(1-\delta _{i})X^{\top }_i\stackrel{P}{\longrightarrow }(EX^{\top }-E\delta X^{\top })$, it is not difficult to get

$$\begin{aligned} \begin{array}{lll} H_{n3} &{}=&{}\displaystyle (EX^{\top }-E\delta X^{\top })\sum \limits _S w(S|\Delta ) R_S\Sigma \Sigma _0^{-1}\cdot \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}\delta _{i}X_i\varepsilon _i\\ &{}&{}\displaystyle +(EX^{\top }-E\delta X^{\top })\sum \limits _S w(S|\Delta )A_S\left( \begin{array}{c} 0\\ \eta \end{array} \right) +o_p(1). \end{array} \end{aligned}$$

This together with $H_{n1}$ and $H_{n2}$ implies that

$$\begin{aligned} \begin{array}{lll} \sqrt{n}(\hat{\theta }-\theta ) &{}=&{}\displaystyle \frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}[\delta _{i}-(EX^{\top }-E\delta X^{\top })\sum \limits _S w(S|\Delta ) R_S\Sigma \Sigma _0^{-1}\delta _{i}X_i]\varepsilon _i \\ &{}&{}\displaystyle +\frac{1}{\sqrt{n}}\sum \limits _{i=1}^{n}(X^{\top }_i\beta _0-\theta ) +(EX^{\top }-E\delta X^{\top })\sum \limits _S w(S|\Delta )A_S\left( \begin{array}{c} 0\\ \eta \end{array}\right) . \end{array} \end{aligned}$$

Then, Theorem 4 follows from the central limit theorem. This completes the whole of the proof.