Optimal signaling with cheap talk and money burning

Abstract

We study Sender-optimal signaling equilibria with cheap talk and money-burning. Under general assumptions, the Sender never uses money-burning to reveal all states, but always wants to garble information for at least some states. With quadratic preferences and any log-concave density of the states, optimal communication is garbled for all states: money-burning, if used at all, is used to adjust pooling intervals. This is illustrated by studying in depth the well-known uniform-quadratic case. We also show how the presence of a cost of being “caught unprepared” that gives rise to a small change in a common assumption on the Receiver’s utility function makes full revelation through money-burning Sender-optimal.

1 Introduction

There are many situations in which decision makers lack relevant information, while those that possess the information have a biased interest in the decision that must be taken. DellaVigna and Gentzkow (2010) provide numerous examples where informed parties, like sellers or lobbyists, try to influence uninformed parties, e.g., consumers or politicians. In such situations, what is the optimal strategy of the informed party, the Sender, to influence the decision-maker, the Receiver? We study how a Sender makes optimal use of two common instruments—cheap talk and money burning—to influence a Receiver.

Money burning is a common euphemism for self-imposed losses in utility, see, e.g., Austen-Smith and Banks (2000). An often cited example of money burning is brand advertising as the content of the advertisement is less important than the fact that money was spent on it.¹ However, as losses are self-imposed, money burning is also readily accessible in many other social situations, e.g., when a lobbyist goes out of his way to reach a member of parliament or when a political prisoner goes on hunger strike to show his commitment to a cause.²

We conduct our analysis in the cheap talk model of Crawford and Sobel (1982), CS from now on, augmented with money burning. The resulting model was first studied by Austen-Smith and Banks (2000), ASB from now on. ASB show that the option to burn money expands the set of equilibria enormously and makes, e.g., full revelation a possible equilibrium outcome. We proceed further and establish which equilibrium is best, in expected terms, from the Sender’s perspective.³ In particular, we address the following issues. Under what conditions is it optimal for the Sender to burn money to fully reveal all her private information about the state? Under what conditions is it optimal to fully reveal a particular interval of states? Can it be optimal for the Sender to rely exclusively on cheap talk, and not to use any money burning at all? How does the use of money burning relate to the degree of conflict between the Sender and the Receiver?

Our main results are as follows. Suppose we have an equilibrium in which the Sender separates states in an interval. We derive a condition such that, if satisfied, we can construct another equilibrium in which the Sender pools some of the states in that interval and that gives him a higher expected utility. Two results follow immediately. First, although money burning makes perfect separation feasible, as is shown in ASB and Kartik 2007, we show it is never optimal for the Sender. Because of the misalignment between the Sender and the Receiver, separation requires increasing amounts of money burning. Irrespective of the Sender’s utility function and the state distribution, the Sender benefits from garbling information for at least some states. The second result is that in a large class of models, including models with preferences represented by quadratic loss functions in combination with any density of the states that is log-concave, the Sender does not use money burning to separate an interval of states.⁴ That is, in this class of models, adding money burning as an instrument of communication does not lead the Sender to reveal any state precisely. Communication is garbled for all states. In other words, to the extent that a lobbyist can choose her lobbying strategy, the member of parliament cannot deduce the exact state from his interaction with the lobbyist.

It then logically follows that, within that class, if money burning is used at all in the optimal equilibrium, it is used (i) to re-arrange pooling intervals relative to what they would have been in the absence of money burning, and possibly (ii) to include one or more additional pooling intervals. To better understand the logic of these two uses of money burning, we next focus on a well-known instance of a log-concave density, the uniform density, and assume a quadratic loss function, as much theory and applied work does. Recall that Crawford and Sobel (1982) show that if cheap talk is the only instrument of communication, when the degree of conflict between Sender and Receiver decreases, the quality of communication can increase. In particular, if the degree of conflict drops below specific threshold levels, the maximum number of distinct actions that the Sender can induce the Receiver to take through verbal communication goes up by one.

We show that the Sender only burns money if her degree of conflict with the Receiver is close to one of these threshold values. If it is just larger than such a threshold value, burned money is particularly cost-effective in inducing the Receiver to take an additional action, as a slight reduction in the degree of conflict would already have led to an increase in the number of actions in the absence of money burning. That is, an additional interval is injected into the equilibrium partition. If the degree of conflict is just below a threshold value, it is not optimal to use money burning to increase the number of actions that the Receiver wants to take. Instead, the Sender burns money to induce the Receiver to better align his actions with her own interests. When the degree of conflict decreases, optimal equilibria with and without money burning alternate. We conjecture that this structure also holds for other log-concave densities. We conclude by showing how a discontinuity in the Receiver’s utility function makes full revelation through money burning the Sender’s optimal strategy.

In this paper we focus on Sender-optimal equilibria. We do so for a number of reasons. It is a focal extremal point of the equilibrium set. The other focal extremal point is the Receiver-optimal equilibrium. Clearly, from the Receiver’s perspective, a perfectly separating equilibrium is optimal as he does not incur the costs of money burning. Second, in the game that we study there is a channel for communication directed from the Sender to the Receiver. If the Sender also uses this channel to announce ex ante what signaling strategy it will use, it is natural to focus on the Sender-optimal equilibrium strategy. This requires only a moderate degree of commitment, as the Sender only commits to play an equilibrium strategy, rather than possibly a non-equilibrium strategy. Moreover, as we show towards the end of the paper, the equilibrium signaling strategy that maximizes the sum of expected utilities of Sender and Receiver is qualitatively similar to the one that is Sender-optimal. Finally, by focusing on the signaling equilibrium strategy that is optimal from the informed party’s perspective we can usefully contrast it with the screening equilibrium strategy that is optimal from the uninformed party’s perspective and that has been studied in Krishna and Morgan (2008). We discuss that paper in the next section.

The rest of the paper is organized as follows. Section 2 reviews the related literature, and Sect. 3 sets up the model which is analyzed in Sects. 4 and 5. Section 6 discusses when separation can be Sender-optimal. Section 7 concludes. Appendix A contains all proofs.

2 Related literature

ASB is the seminal paper on signaling with cheap talk and money burning, and we make use of one of its important finding: the set of states that give rise to a given action is convex. The main contribution of ASB is to prove the existence of a special class of equilibria in which money burning takes place. ASB establish that thanks to money burning, one can “squeeze in separating segments at the far end of any ... equilibrium partition” of a game studied in CS in which the Sender can use only cheap talk (ASB, p. 7). It then follows that full revelation is also an equilibrium outcome. Austen-Smith and Banks (2002) study some welfare results for the uniform-quadratic case. They establish that the Sender prefers the most-informative cheap talk equilibrium over a fully separating equilibrium using money burning. We extent their results by showing that, with general densities and preferences, the Sender never prefers using money burning to fully separate, and by showing which equilibrium she prefers in the uniform quadratic case.

For the model used in ASB, Kartik (2007) shows that cheap talk can be influential, i.e., induce at least two different actions, with money burning if and only if it can be influential without money burning. He also proves the conjecture stated in ASB that if the amount of money the Sender can burn shrinks to zero, the set of equilibria with burned money shrinks to the set of pure cheap talk equilibria.

Sender-optimal strategies have also been the focus in other contexts. Recently, Rayo and Segal (2010) and Kamenica and Gentzkow (2011) derived Sender-optimal communication strategies when she can commit to truthfully reveal her private information. This contrasts with our assumption that a Sender cannot commit to a strategy. Like us, Eső and Galambos (2013) study a Sender who has access to cheap talk and a second means of communication. Whereas we study money burning as the second means, they study the possibility making information hard at a cost that is independent of the true state. In the presence of hard information, full revelation can only be an equilibrium if disclosure costs equal zero, whereas full revelation always exists in case of money burning.⁵

The Sender–Receiver problem has also been approached as a screening problem. The focus has been on the uninformed principal offering a compensation contract or a delegation contract.⁶ Ottaviani (2000) and Krishna and Morgan (2008) study compensation contracts, in which the principal compensates the agent for information that she provides. Ottaviani (2000) shows, for the uniform-quadratic case, that the principal can guarantee full revelation, but that he is better off with delegation. Krishna and Morgan (2008) study characteristics of the optimal contract in general settings. Their so-called imperfect commitment case is the relevant case for a comparison with our paper. In that case, the principal cannot commit to a decision as a function of the message he receives, but can commit to a monetary transfer as a function of the message. They show that, in general, the principal is better off by offering a contract that induces the agent to pool for high states than one that leads to full revelation. Although pooling gives rise to a reduction in utility for high states, this is more than compensated by the reduction in transfers that are needed to induce truth telling for lower states. In our set-up, the Sender can perfectly reveal her information about the state through money burning but does not find it in her interest to do so because pooling some states gives rise to a local gain in utility that more than compensates any possible additional money that needs to be burned in all the other states. The balance of local losses and global gains is such that in the uniform-quadratic case, the principal in Krishna and Morgan (2008) never pays for vague information, only for precise information. In the same uniform-quadratic case, the Sender in our model does not burn money to separate an interval of states. Instead, it is only cost-effective to burn money to adjust the intervals of the semi-pooling communication strategy and, possibly, to adjust their number.

3 The model

The model is that of ASB. In stage 1, the state of nature $t\in [ {0,1} ]$ is privately revealed to the Sender. This state is distributed according to a distribution function F(t) that has a strictly positive and continuously differentiable density function $f( t )\equiv F'( t )$. In stage 2, the Sender sends the Receiver a signal $\sigma =( {m,b} )$, which consists of a costless message m from some continuum M, and a costly message $b\ge 0$ (money burning). The content of the message m is unverifiable, i.e., cheap talk, and b is publicly observed and, hence, verifiable.

Let $\sigma ( t )=( {m,b} )$ be a pure signaling strategy. Having observed ( m, b ) the Receiver forms posterior beliefs about the state, denoted by the CDF $G( {z\vert \,m,b} )\equiv \Pr [ {t\le z\vert m,b} ]$. Then, in stage 3, the Receiver takes an action a. Let $\alpha ( {m,b} )$ be his pure strategy. Preferences of the Sender and the Receiver are given by the following utility functions $U^{\mathrm{S}}$ and $U^{\mathrm{R}}$, respectively:

$$\begin{aligned} U^{\mathrm{S}}\left( {a,t,m,b} \right) =u\left( {a,t,x} \right) -b,\quad \hbox { and }\quad U^{\mathrm{R}}\left( {a,t,m,b} \right) =u^{\mathrm{R}}\left( {a,t} \right) , \end{aligned}$$

where $x>0$ is a measure of the extent to which the players’ preferences are misaligned.

Following Austen-Smith and Banks (2000), we assume that u( a, t, x ) and $u^{\mathrm{R}}( {a,t} )$ are three times continuously differentiable, are strictly concave and not monotone in a, and have strictly positive cross partial derivatives $u_{at} >0$, $u_{ax} >0$, $u_{at}^{\mathrm{R}} >0$. Let $a^{\mathrm{R}}( t )$ denote the action that is best from the Receiver’s perspective in state t:

$$\begin{aligned} a^{\mathrm{R}}\left( t \right) =\mathop {\hbox {argmax}}\limits _{a} \,u^{\mathrm{R}}\left( {a,t} \right) , \end{aligned}$$

and let $a^{\mathrm{S}}( {t,x} )$ be the action that is best from the Sender’s perspective in state t:

$$\begin{aligned} a^{\mathrm{S}}\left( {t,x} \right) =\mathop {\hbox {argmax}}\limits _{a} \,u\left( {a,t,x} \right) . \end{aligned}$$

Under our assumptions, both $a^{\mathrm{R}}( t )$ and $a^{\mathrm{S}}( {t,x} )$ are finite and strictly increasing, and we assume, in addition, that $a^{\mathrm{S}}( {t,x} )>a^{\mathrm{R}}( t )$, for all $x>0$ and $t\in [ {0,1} ]$. In order to simplify the exposition, we assume w.l.o.g. that the actions are labeled in such a way that $a^{\mathrm{R}}( t )=t$ (this can always be done due to the monotonicity of $a^{\mathrm{R}}( t )$). The ex-ante expected utilities from a strategy profile $( {\sigma ,\alpha } )$ are denoted as follows:

$$\begin{aligned}&V^{\mathrm{S}}\left( {\sigma ,\alpha } \right) \equiv \text{ E }\left[ {U^{\mathrm{S}}\left( {a,t,m,b} \right) } \right] =\text{ E }\left[ {u\left( {\alpha \left( {\sigma \left( t \right) } \right) ,t,x} \right) } \right] -\text{ E }\left[ {b\left( t \right) } \right] , \end{aligned}$$

(1)

$$\begin{aligned}&V^{\mathrm{R}}\left( {\sigma ,\alpha } \right) \equiv \text{ E }\left[ {U^{R}\left( {a,t,m,b} \right) } \right] =\text{ E }\left[ {u^{\mathrm{R}}\left( {\alpha \left( {\sigma \left( t \right) } \right) ,t} \right) } \right] . \end{aligned}$$

(2)

An equilibrium ${\Omega }=\left\langle \sigma ( t ),\alpha ( {m,b} ),G( {t{\vert }m,b} )\right\rangle$ is (i) a signaling strategy of the Sender $\sigma ( t )$ that is optimal for every state t given the Receiver’s action strategy $\alpha ( {m,b} )$, (ii) an action strategy $\alpha ( {m,b} )$ that is optimal given beliefs $G( {t{\vert }\,m,b} )$, and (iii) Receiver’s beliefs $G( {t{\vert }\,m,b} )$ that are consistent with $\sigma ( t )$ for signals ( m, b ) on the equilibrium path. Ex-ante utilities of the Sender and the Receiver in equilibrium ${\Omega }$ are denoted by $V^{\mathrm{S}}( {{\Omega }} )$ and $V^{\mathrm{R}}( {{\Omega }} )$ respectively. An equilibrium signaling strategy is denoted by $\sigma ^{\Omega }$. We are interested in the equilibrium that generates the highest ex-ante expected utility for the Sender.

4 Characteristics of Sender-optimal equilibria

ASB (p. 7) establish that all equilibria have the following structure: there is a partition $( {B_{0} \equiv 0,A_{1} ,B_{1} ,\ldots ,B_{N} ,A_{N+1} \equiv 1} )$ with $B_{i-1} \le A_{i} <B_{i} \le A_{i+1}$ for all $i\in I=\{ {1,\ldots ,N} \}$, such that the Sender pools all states $t\in ( {A_{i} ,B_{i} } )$ by sending a message $m( t )=m_{i}^{\mathrm{P}}$ (with the meaning “the state t belongs to interval $( {A_{i} ,B_{i} } )$”) and by burning identical amounts of money $b_{i}^{\mathrm{P}}$. If instead $t\in ( {B_{i} ,A_{i+1} } )$, she separates by sending distinct messages $m( t )=m^{\mathrm{S}}( t )$ (with the meaning “the state is t”) and by burning distinct amounts of money $b( t )=b^{\mathrm{S}}( t )$. As any partition is uniquely defined by its collection of pooling intervals, we will abuse terminology by referring to the collection $P( {{\Omega }} )=\{ {( {A_{i} ,B_{i} } )\vert i\in I} \}$ as the partition of equilibrium ${\Omega }$. For example, a separating equilibrium corresponds to $P=\emptyset$, and a complete pooling equilibrium corresponds to $P=\{ {( {0,1} )} \}$.

ASB establish the existence of a special class of equilibria that can be obtained from the pure cheap talk equilibria studied in CS by squeezing in “separating segments at the far end of any CS partition” (ASB, p. 7).⁷ We are interested in how the Sender can best combine cheap talk and money burning and, therefore, cannot limit ourselves to a special class of equilibria. The next proposition is the first step towards a Sender-optimal equilibrium.

Proposition 1

For any partition $P_{0}$, there is an equilibrium ${\Omega }_{0}$ such that $P_{0} =P( {{\Omega }_{0} } )$.

The Sender can arbitrarily choose any number of non-overlapping pooling intervals. Let $S^{\mathrm{P}}$ denote the union of these intervals and let $S^{\mathrm{S}}=[ {0,1} ]\backslash S^{\mathrm{P}}$ denote the set of states for which the Sender separates. Proposition 1 means, for example, that full separation is an equilibrium.

According to Proposition 1, we can search for the Sender-optimal equilibrium by optimizing $V^{\mathrm{S}}( {\sigma ,\alpha } )$ over the set of all possible partitions, subject to incentive compatibility constraints and non-negativity of burned money constraints. Note that Proposition 1 does not imply that the Sender can induce the Receiver to take any set of actions. For example, if the Sender wants to induce the Receiver to take a single action, then she must pool, and thus this action can only equal the Receiver’s optimal action in case of complete pooling.

On the current level of generality, when both players have utility functions u( a, t, x ) and $u^{\mathrm{R}}( {a,t} )$ that are completely independent from each other, the analysis is very complicated and results are not easy to interpret. We assume in what follows that the Receiver’s utility is a quadratic loss function $u^{\mathrm{R}}( {a,t} )=-( {t-a} )^{2}$ while keeping the Senders’ utility u( a, t, x ) arbitrary. We define:

$$\begin{aligned} {\varPsi } \left( t \right) \equiv \frac{2u_{tta} \left( {t,t,x} \right) +u_{taa} \left( {t,t,x} \right) }{2u_{ta} \left( {t,t,x} \right) }. \end{aligned}$$

Since function ${\varPsi } ( t )$ vanishes for quadratic utility functions u( a, t, x ), it can be interpreted as a measure of a difference between utility function u( a, t, x ) and its second-order approximation, i.e., as a measure of higher-order terms in the Tailor expansion of u( a, t, x ). Suppose we have an equilibrium in which the Sender separates states in an interval. If a simple condition is satisfied, then we can construct another equilibrium in which the Sender pools some of the states in that interval and that gives her a higher expected utility.

Proposition 2

Consider an equilibrium ${\Omega }$ in which the Sender separates all states in an interval ( B, A ). If the following condition holds for some $t\in ( {B,A} )$:

$$\begin{aligned} - \frac{{f\left( t \right) }}{{F\left( t \right) }} + \frac{{f^{\prime }\left( t \right) }}{{f\left( t \right) }}< {\varPsi } \left( t \right) < \frac{{f\left( t \right) }}{{1 - F\left( t \right) }} + \frac{{f^{\prime }\left( t \right) }}{{f\left( t \right) }}, \end{aligned}$$

(3)

then the Sender benefits from pooling some states in that interval, so that ${\Omega }$ is not optimal.

Fig. 1

Illustration for Proposition 2

To gain intuition for the condition in Proposition 2, and to understand how local changes in ( B, A ) have global consequences—as suggested by the appearance of F(t) and $1-F( t )$ in the condition—we consider an equilibrium ${\Omega }$ in which the Sender separates all states in ( B, A ). The utility $v^{\Omega }( t )$ that the Sender gets in ( B, A ) is indicated in Fig. 1 by the bold line.

We now try to construct another equilibrium, $\Omega ^{\varepsilon }$, that is obtained from $\Omega$ by adding a pooling interval $( {A-\varepsilon ,A} )$, i.e., $P( {{\Omega }^{\varepsilon }} )=P( {{\Omega }} )\cup \{ {( {A-\varepsilon ,A} )} \}$, and by imposing that $v^{\Omega ^{\varepsilon }}( {A-\varepsilon } )=v^{\Omega }( {A-\varepsilon } )$. In other words, we try to leave the Sender’s utility unchanged for $t\in ( {B,A-\varepsilon } ]$ and, instead of separating, we let the Sender pool all states $t\in ( {B,A-\varepsilon } ]$ in ${\Omega }^{\varepsilon }$. In ${\Omega }^{\varepsilon }$, the Receiver’s best response action to a message that the state is in $( {A-\varepsilon ,A} )$ is strictly larger than his best response action to the Senders’ message that $t=A-\varepsilon$. Because of $u_{ta} >0$, this means that in a right neighborhood of $t=A-\varepsilon$, the Sender benefits from pooling, see the thin (solid and dashed) lines representing two possibilities for $v^{\Omega ^{\varepsilon }}( t )$ in Fig. 1.

Because of the equilibrium conditions, local changes of equilibrium strategies in the interval $( {A-\varepsilon ,A} )$ have global consequences: pooling these states may make additional money burning necessary for states to the right or to the left of the pooling interval, and Fig. 1 explains why. For $t=A$, the difference in utility $\varphi ( A )=v^{\Omega }( A )-v^{\Omega ^{\varepsilon }}( A )$ depends on the Sender’s utility function and the distribution of states. In the proof of Proposition 2, we show that for a pooling interval of marginal length $\varepsilon$, the change in utility is given by

$$\begin{aligned} \varphi \left( A \right) = \frac{{u_{{ta}} \left( {A,A,x} \right) }}{2}\left( {{\varPsi } \left( A \right) - \frac{{f^{\prime }\left( A \right) }}{{f\left( A \right) }}} \right) . \end{aligned}$$

Since $\varphi ( A )=0$ for a uniform-quadratic model, the term $( {{\varPsi } ( A ) - f^{\prime }( A )/f( A )} )$ can be interpreted as a measure of a difference between the current model and its uniform-quadratic approximation. Suppose that ${\varPsi } ( A ) > f^{\prime }( A )/f( A )$ so that $\varphi ( A )>0$. Then, without any changes in the signaling strategy to the right of A, if the state is just below A, the Sender would have liked to slightly exaggerate and report a state just above A. One way to make sure that ${\Omega }^{\varepsilon }$ is an equilibrium is to adjust the Sender’s signaling strategy so that in all states $t>A$, she burns an additional amount of money that is equal to $\varphi ( A )$. This restores the continuity of the utility function at $t=A$, and guarantees that the equilibrium conditions continue to hold for all $t>A$. Hence, an equilibrium ${\Omega }^{\varepsilon }$ with a pooling segment of marginal length yields more utility than ${\Omega }$ if the additional amount of money burned $( {1-F( A )} )\varphi ( A )$ is smaller than the gain in utility which turns out to be $\frac{1}{2}u_{ta} ( {A,A,x} )f( A )$. That is, if the condition $0< {\varPsi } - \frac{{f^{\prime }}}{f} < \frac{f}{{1 - F}}$ holds for $t=A$, the Sender benefits from pooling some states of the separating segment.

Alternatively, if $\varphi ( A )<0$ because of ${\varPsi } ( A ) < \frac{{f^{\prime }( A )}}{{f( A )}}$, the Sender’s utility gets increased at $t=A$ due to pooling the states; Fig. 1 represents this case by the dashed line. Without any further changes to the Sender’s money burning strategy, she would now prefer to underreport the state if she were to observe values of t slightly above $t=A$. One way to make sure that ${\Omega }^{\varepsilon }$ is an equilibrium is to increase amounts of money burnt in all states $t<A$ (it may not be possible to burn less money for $t>A$ because, e.g., in some states above A the Sender does not burn any money at all in ${\Omega }$). For pooling some of the states to be optimal, the additional cost of money burning $( {-F( A )\varphi ( A )} )$ should be smaller than the gain $\frac{1}{2}u_{ta} ( {A,A,x} )f( A )$, i.e., $- \frac{f}{F}< {\varPsi } - \frac{{f^{\prime }}}{f} < 0$ evaluated for $t=A$.

Proposition 2 has two important consequences. First, by applying the condition to the whole interval [ 0, 1 ] it follows that full revelation (i.e., revealing all states) is never optimal. The Sender benefits from some vagueness by pooling at least some interval of states. Pooling some states give rise to a local gain in utility that more than compensates any possible additional money that needs to be burned globally (i.e., outside the interval of pooled states). Thus, combining Propositions 1 and 2 we conclude that:

Corollary 1

Even though the perfectly separating equilibrium is always feasible, it is never Sender-optimal.

The second consequence deals with the class of state distributions with log-concave densities and the much-used quadratic loss function. With such preferences, ${\varPsi } ( t )=0$ for all t. Moreover, a log-concave density has an increasing hazard rate and a decreasing reversed hazard rate, see Bagnoli and Bergstrom (2005). This suffices to show that $- \frac{{f( t )}}{{F( t )}} + \frac{{f^{\prime }( t )}}{{f( t )}} < 0$ and that $\frac{{f( t )}}{{1 - F( t )}} + \frac{{f^{\prime }( t )}}{{f( t )}} > 0$ for all t. Thus,

Corollary 2

Let the utility function u( a, t, x ) of the Sender be a quadratic loss function, i.e., $u( {a,t,x} )=-( {a-t-x} )^{2}$, and let the states have a log-concave density f(t). Then, in an optimal equilibrium the Sender does not separate any interval of states.

Corollary 2 implies that, in a large class of models (including the uniform-quadratic case), communication is garbled in a Sender-optimal equilibrium, for all states. What role can money burning play in an optimal equilibrium, if it cannot lead to separation? Logically, two possibilities remain. It is either not used at all, or it is used but only to re-arrange the pooling intervals in the equilibrium partition, relative to what they would have been in the absence of money burning. In the latter case, money burning may also give rise to a different number of pooling intervals. To better see whether and how the Sender uses money burning, in the next section we derive the optimal equilibrium for the well-known uniform-quadratic case.

Fig. 2

Illustration for Proposition 3

5 Sender-optimal equilibrium in the uniform-quadratic case

We use asterisks to denote variables in the Sender’s optimal equilibrium ${\Omega }^{*}$. The next proposition characterizes the Sender’s maximization problem.

Proposition 3

In the uniform-quadratic case, an optimal equilibrium ${\Omega }^{*}$ always exists. Its equilibrium partition $P^{*}=P( {{\Omega }^{*}} )$ contains a finite number $N^{*}$ of pooling intervals $( {A_{i} ,A_{i+1} } )$ that fully cover the state space [ 0, 1 ]. Number $N^{*}$ and marginal states $\{ {A_{i} } \}$, $i=1,\ldots ,N^{*}$ solve the following maximization problem:

$$\begin{aligned}&\mathop {\max }\limits _{N,\left\{ {A_{i} } \right\} ,c} V^{\mathrm{S}}=-c-x^{2}-x+\frac{1}{6}\mathop {\sum }\limits _{i=1}^{N} \left( {A_{i+1} -A_{i} } \right) ^{3} \end{aligned}$$

(4)

$$\begin{aligned}&\text {subject to}:b_{i}^{\mathrm{P}} =\left( {A_{i+1} +A_{i} } \right) x-\frac{1}{4}\left( {A_{i+1} -A_{i} } \right) ^{2}+c\ge 0 \end{aligned}$$

(5)

In this optimization, the Sender chooses a number of intervals N, positions of $( {N-1} )$ distinct marginal states, $\{ {A_{i} } \}$, and a parameter c. Figure 2 shows that there is a trade-off in the above optimization. The bold solid curve represents a utility function $v^{\Omega _{1} }( t )$ of the Sender in state t, for an equilibrium ${\Omega }_{1}$ with (at least) three pooling intervals in the partition, $( {t_{i} ,t_{i+1} } )$, $( {t_{i+1} ,t_{i+2} } )$, and $( {t_{i+2} ,t_{i+3} } )$. In each pooling interval, the (smallest) vertical distance between the graph of $v^{\Omega _{1} }( t )$ and the horizontal axis is equal to $b_{i}^{\mathrm{P}}$. The ex-ante expected utility of the Sender is $V^{\mathrm{S}}$ the (negative of) the shaded area above $v^{\Omega _{1} }( t )$.

By merging two intervals $( {t_{i} ,t_{i+1} } )$ and $( {t_{i+1} ,t_{i+2} } )$ into one single pooling interval $( {t_{i} ,t_{i+2} } )$, we get a new equilibrium ${\Omega }_{2}$, with the utility function $v^{\Omega _{2} }( t )$ (bold dashed curve). As one can see, this has a positive effect on $V^{\mathrm{S}}$. If however, we merge all three intervals into a single pooling interval $( {t_{i} ,t_{i+3} } )$ without changing parameter c, the amount of money to be burned in states $t\in ( {t_{i} ,t_{i+3} } )$ would have become negative (thin dotted curve, which goes above the horizontal axis). Thus, the value of c must be increased so as to just make the graph of $v^{\Omega _{3} }( t )$ touching the horizontal axis, (thin solid line).

The trade-off the Sender faces can now be seen. On the one hand, she benefits from having fewer but longer pooling intervals in an equilibrium, since this increases the sum in (4). On the other hand, such a strategy would potentially require a larger value of parameter c, i.e., more burned money in all states, due to (5), which lowers her utility $V^{\mathrm{S}}$ directly.

Proposition 4 below gives the main features of the equilibrium. It shows for which degree of misalignment x the Sender actually burns money in the optimal equilibrium. It also shows how the optimal equilibrium partition $P( {{\Omega }^{*}} )$ is related to that of CS. Before we state the proposition, a small digression on the Crawford and Sobel (1982) model is needed. Recall that in CS, money burning is absent and communication can only take place through cheap talk. In equilibrium there is an upper bound on the number of distinct messages that the Sender can use. For every integer $N\ge 2$, let us define $x_{N}$ as follows:

$$\begin{aligned} x_{N} \equiv \frac{1}{2N\left( {N-1} \right) }. \end{aligned}$$

(6)

Without the option to burn money, if the degree of misalignment satisfies $x\in [ {x_{N+1} ,x_{N}} )$, then for every value of $n=1,\ldots ,N$ there exists an equilibrium in which the Sender can induce the Receiver to take exactly n actions. For every x, the equilibrium with the highest number of messages N, is called the most informative equilibrium, denoted by ${\Omega }^{\mathrm{CT}}$. For any given value of x, the Sender prefers the equilibrium ${\Omega }^{\mathrm{CT}}$ with the largest number of messages N. Let $\sigma ^{\mathrm{CT}}$ denote the most informative cheap talk strategy.

It turns out that the structure of $\sigma ^{*}$ is closely related to the structure of $\sigma ^{\mathrm{CT}}$. The intuition is that an additional communication instrument—money burning—can be used to alleviate the bound on the number N of distinct actions that the Sender can induce the Receiver to take. This is particularly cost-effective for those values of x for which a slight reduction in x would already have led to an increase in the number of such actions in the absence of money burning. Alternatively, money burning can be used to change the lengths of the intervals of the pure cheap talk partition $P^{\mathrm{CT}}$. This is particularly beneficial for values of x for which an additional interval has just emerged in $P^{\mathrm{CT}}$. This intuition is borne out by the next proposition.

Proposition 4

For every $N\ge 4$ there exist a $\underline{y} _{N}$ and $\bar{y}_{N}$ satisfying $x_{{N + 1}}< \bar{y}_{{N + 1}}< \underline{y}_{N}< x_{N} < \bar{y}_{N}$, such that in an optimal equilibrium $\Omega ^{*}$:

• (a) if $x \in [ {x_{N} ,\bar{y}_{N} } )$, the Sender burns money. Compared with ${\Omega }^{\mathrm{CT}}$, she induces one additional action, $N^{*}=N+1$, $P^{*}\ne P^{\mathrm{CT}}$.

• (b) if $x\in ( \underline{y}_{N} ,x_{N} )$, the Sender burns money. Compared with ${\Omega }^{\mathrm{CT}}$, she induces the same number of actions, $N^{*}=N$ but re-arranges the partition, $P^{*}\ne P^{CT}$.

Proposition 4 illustrates how the Sender uses money burning to adjust the partition in an optimal equilibrium even if she does not use it to reveal any specific state. This result will qualitatively carry over to situations with other log-concave densities.

In what follows we study in more depth how, for the uniform-quadratic case, money burning shapes the equilibrium partition.

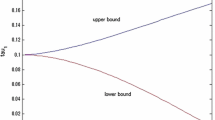
It follows from the proof of Proposition 4 that in the uniform-quadratic case money burning is used in the second interval only. Figure 3 illustrates how, for different values of x, money burning is present or absent in the optimal equilibrium ${\Omega }^{*}$ in an alternating pattern. It shows the amount of money burned $b_{2}^{\mathrm{P}}$ in the second interval of ${\Omega }^{*}$ (thin line, right scale), and the ex-ante probability that the Sender burns money, $\Pr [ {b( t )>0} ]$ (thick line, left scale), which is the length of the second interval provided $b_{2}^{\mathrm{P}} >0$. One can see, e.g., that at $x = \bar{y}_{4} = \frac{1}{{22}}$, the length of this interval is zero, and increases with further reductions in x. At $x=\underline{y}_{4} \approx 0.039$, the Sender burns money for nearly 20% of the states. The amount of money burned $b_{2}^{\mathrm{P}}$ is strictly positive at $x = \bar{y}_{4}$, and decreases with further reductions in x.

Fig. 3

The amount of money burned in the second interval $b_{2}^{\mathrm{P}}$, and the ex-ante probability that money will be burned $\Pr [ {b^{*}( t )>0} ]$, as functions of x

If $x > \bar{y}_{4} = \frac{1}{{22}}$, money burning cannot improve upon the most informative cheap talk equilibrium. That is, for money burning to improve the Sender’s utility, the interests between Sender and Receiver should be sufficiently well aligned such that unaided cheap talk communication allows her to induce at least three actions.

We illustrate the two parts of Proposition 4 with one figure each. Figure 4 is drawn for $x=0.042$. Since $x \in ( {x_{4} ,\bar{y}_{4} } )$, the most informative cheap talk equilibrium ${\Omega }^{\mathrm{CT}}$ has three intervals (with up to three digits of accuracy):

$$\begin{aligned} P^{\mathrm{CT}}=\left\{ {\left( {0,0.165} \right) ,\left( {0.165,0.499} \right) ,\left( {0.499,1} \right) } \right\} , \end{aligned}$$

whereas the optimal equilibrium ${\Omega }^{*}$ has four intervals:

$$\begin{aligned} P^{*}=\left\{ {\left( {0,0.066} \right) ,\left( {0.066,0.176} \right) ,\left( {0.176,0.504} \right) ,\left( {0.504,1} \right) } \right\} . \end{aligned}$$

Figure 4 shows the ex-post equilibrium utility functions $v^{\Omega }( t )$ of the Sender in ${\Omega }^{\mathrm{CT}}$ and ${\Omega }^{*}$, and the money burning function $b^{*}( t )$. She burns $b_{2}^{P} \approx 5.5\times 10^{-3}$ in the second interval of $P^{*}$.

Figure 5 is drawn for $x=0.04$. Since $x\in ( \underline{y}_{4} ,x_{4})$, it illustrates a situation in which the Sender does not burn money to induce the Receiver to take a larger number of actions, but to improve the existing actions. Indeed, the most informative cheap talk strategy $\sigma ^{\mathrm{CT}}$ has four distinct messages,

$$\begin{aligned} P^{\mathrm{CT}}=\left\{ {\left( {0,0.01} \right) ,\left( {0.01,0.18} \right) ,\left( {0.118,0.51} \right) ,\left( {0.51,1} \right) } \right\} , \end{aligned}$$

and so does the optimal equilibrium strategy in the presence of money burning,

$$\begin{aligned} P^{*}=\left\{ {\left( {0,0.035} \right) ,\left( {0.035,0.185} \right) ,\left( {0.185,0.512} \right) ,\left( {0.512,1} \right) } \right\} . \end{aligned}$$

The figure shows ex-post equilibrium utility functions $v^{\Omega }( t )$ of the Sender in ${\Omega }^{\mathrm{CT}}$ and ${\Omega }^{*}$, and the money burning function $b^{*}( t )$. She burns $b_{2}^{P} \approx 2.0\times 10^{-3}$ in the second interval of $P^{*}$.

Fig. 4

Equilibria ${\Omega }^{\mathrm{CT}}$ and ${\Omega }^{*}$ for $x=0.042$

Fig. 5

Equilibria ${\Omega }^{\mathrm{CT}}$ and ${\Omega }^{*}$ for $x=0.04$

Above, we have derived the Sender’s optimal equilibrium. The Receiver’s optimal equilibrium is, clearly, the perfectly separating equilibrium. Indeed, the ex-ante expected utility $V^{\mathrm{R}}( {{\Omega }} )$ of the Receiver equals:

$$\begin{aligned} V^{\mathrm{R}}\left( {{\Omega }} \right) =\text{ E }\left[ {u\left( {\alpha \left( {\sigma \left( t \right) } \right) ,t,0} \right) } \right] =-\frac{1}{12}\sum \limits _{i} \left( {B_{i} -A_{i}} \right) ^{3}. \end{aligned}$$

The Receiver experiences a utility loss from any pooling intervals and, therefore, obtains his first best level of utility in the perfectly separating equilibrium. A natural question that arises is what equilibrium is best from a social welfare perspective. Define the social welfare function as follows:

$$\begin{aligned} V^{\mathrm{SW}}\left( {{\Omega }} \right) \equiv \left( {1-\alpha } \right) V^{\mathrm{R}}\left( {{\Omega }} \right) +\alpha V^{\mathrm{S}}\left( {{\Omega }} \right) ,\quad \alpha \in \left( {0,1} \right) . \end{aligned}$$

Thus,

$$\begin{aligned} V^{\mathrm{SW}}\left( {{\Omega }} \right) =\alpha \left( {-\left( {c+x^{2}+x} \right) +\frac{3\alpha -1}{2\alpha }\cdot \frac{1}{6}\sum \limits _{i} \left( {B_{i} -A_{i}} \right) ^{3}} \right) , \end{aligned}$$

which only differs from $V^{\mathrm{S}}( {{\Omega }} )$ by the multiplier $\frac{3\alpha -1}{2\alpha }$. As a result of this similarity, Proposition 4 continues to hold for the efficient equilibrium ${\Omega }^{\mathrm{SW}}$, i.e., the equilibrium that maximizes the social welfare function, provided $\alpha >1/3$. Thus, when the Sender’s contribution to the Social Welfare function is at least one third, the number of pooling intervals in ${\Omega }^{\mathrm{SW}}$ is finite, the Sender burns money in at most one interval; if she burns money, she does so in the second interval only; and the values of x for which she does so are close to the values of $x_{N}$. In short, all results from this Section continue to hold qualitatively for this new objective function, although the exact values of the marginal states in the partition supporting the efficient equilibrium, and the exact amounts of money burnt, will be different from ${\Omega }^{*}$.

6 Sender-optimality and separation

In the previous two sections, we have derived conditions under which the Sender prefers communication that is garbled. In this section, we discuss situations in which she might prefer truthful revelation of her private information.

It logically follows from Corollary 1 that for the Sender to reveal truthfully all her private information in an optimal equilibrium, one needs to step outside the model assumed in Sect. 3. The explanation of condition (1) in Sect. 4 suggests one such step. We have explained there that the Sender benefits locally from garbling information, possibly at the expense of more money burning in other states. By garbling information, she induces the Receiver to take a higher action from which she benefits in the right neighborhood of $t=\tilde{t}\equiv A-\varepsilon$, see Fig. 1. This benefit is due to the single-crossing property $u_{ta} >0$. Formally, if we define the difference in the Sender’s utility between these two equilibria as $\theta ( {\varepsilon ,t} ) \equiv v^{{{\Omega }}} ( t ) - v^{{{{\Omega }}^{\varepsilon } }} ( t )$ and $a^{\varepsilon }=\text{ E }[t\vert t\in (\tilde{{t}},A)]$ as the Receiver’s best reply to the pooling message, one can obtain:⁸

$$\begin{aligned} \frac{\partial \theta }{\partial t}(\varepsilon ,t)=-\int _{\tilde{{t}}}^{a^{\varepsilon }} {u_{at} (z,\tilde{{t}},x)dz.} \end{aligned}$$

Clearly, $a^{\varepsilon }>\tilde{{t}}$ and $u_{at}>0$ together imply $\frac{\partial \theta }{\partial t}(\varepsilon ,\tilde{{t}})<0$. Hence, $v^{\Omega }(t)<v^{\Omega ^{\varepsilon }}(t)$ in some right neighborhood of $\tilde{t}$. Of course, this local benefit alone is not sufficient for ${\Omega }^{\varepsilon }$ to be a superior equilibrium to ${\Omega }$ from the Senders’ prospective. Nevertheless, eliminating this local benefit, as we will see, is a way to construct a model in which truthful revelation of all information is optimal for the Sender.

If one keeps the single-crossing property, local gains disappear if the Receiver does not take a higher action when information is garbled, i.e., when $a^{\varepsilon }=\tilde{t}$. This implies that he must get a punishment if the state turns out to be lower than the chosen action. Moreover, it must be so large that even a tiny chance of such a punishment makes the Receiver worse off. Thus, marginal punishment must be infinite, and his utility function must be discontinuous.

We consider, therefore, a variation on the standard quadratic loss function. Let the Receiver’s utility $u^{\mathrm{R}}( {a,t} )$ be given by

$$\begin{aligned} u^{\mathrm{R}}\left( {a,t} \right) =\left\{ {{\begin{array}{ll} -\left( {t-a} \right) ^{2}, &{}\quad if\,\,t\ge a \\ -\left( {t-a} \right) ^{2}-\gamma , &{}\quad if\,\,t<a, \\ \end{array}}} \right. \end{aligned}$$

(7)

with $\gamma >1$. In other words, relative to the standard quadratic loss function, the Receiver experiences additional disutility $\gamma$ if the state t turns out to be lower than the action a he takes.

This discontinuity in the utility function of the Receiver at $a=t$ may arise in policy areas where any deviation from the right level of preparation is costly, but lack of preparation carries a separate, additional cost.⁹ A key example is the reputational damage to the decision maker for being caught ‘unprepared.’ Another example is the loss to society from suffering floods due to dykes of insufficient height: even a small flood causes a discrete drop in welfare. The same discrete drop accompanies terrorism or health risks that have materialized due to insufficient investigative or detection capacity.

The Sender-optimal equilibrium for this uniform-quadratic model with discontinuous loss $\gamma$ turns out to be the perfectly separating equilibrium, as the following proposition states.

Proposition 5

Let $F( t )=t$, $u( {a,t,x} )=-( {t+x-a} )^{2}$, and $u^{\mathrm{R}}( {a,t} )$ be given by (7). Then, in the optimal equilibrium, the Sender burns money to truthfully reveal all states, $P( {{\Omega }^{*}} )=\emptyset$.

Although there remains a conflict between the Sender and the Receiver as to the optimal action in a given state, the change in the utility function of the Receiver makes both of them experiencing a large disutility stemming from communicating ‘vague’ information (i.e., a message from pooling interval). With $\gamma >1$, the Receiver’s best-reply to vague information is the lowest possible action consistent with the message. This aligns their preferences across equilibria, and the perfectly separating equilibrium is the unique Pareto-optimal equilibrium.

Can it be optimal for the Sender to burn money to reveal some of her private information without assuming a discontinuous utility function? This paper does not answer this question, as there is an important asymmetry between showing sub-optimality of pooling and sub-optimality of separation on an interval ( A, B ).

There is a unique way to separate states from an interval ( A, B ), namely by letting the Sender send different signals in all these states. Thus, in order to show that separation on ( A, B ) is sub-optimal, it is sufficient to find one way to pool some of states in ( A, B ) that generates a higher utility for the Sender than the unique way of separation. Our condition (3) represents one such a test.

There are, however, infinitely many ways of pooling states from an interval ( A, B ) into sub-intervals: any partition of ( A, B ) represents one such possibility. Therefore, in order to show that separation on ( A, B ) is optimal, one needs to show that separation is better than any such way of pooling those states. This is much more demanding than what is required for deriving condition (3).

7 Conclusion

In this paper, we study how a privately informed Sender can influence a decision-maker by using both cheap talk messages and money burning. We focus on the Sender’s optimal equilibrium. We have shown that the Sender always garbles some information and that for a large class of cases—including the much studied uniform-quadratic case—the Sender garbles all information. Money burning, although it makes truthful revelation feasible, is either not used at all, or it is used to improve the actions that the Receiver takes by improving upon the partition that she would have used if the Sender could only use cheap talk. If money burning is used to improve the actions, it can also be used in the optimal equilibrium to induce an additional action. We have also shown that if garbled information induces the Receiver to act conservatively because of a discontinuity in his utility function, the Sender optimally reveals all her private information.

De Haan et al. (2015) study how subjects in a laboratory experiment use cheap talk and money burning in the uniform-quadratic case for various degrees of preference misalignment. It is unlikely that any lab experiment will be able to mimic the precise alternating pattern of the presence and absence of money burning as a function of the misalignment parameter that we have shown to be the best from the Sender’s perspective. They do find, however, that Senders have a strong preference for cheap talk, and that they do not burn money to support intervals of full separation.

Appendices

Appendix A

Proof of Proposition 1

In this proof, we use the following lemma, proven in ASB, p. 7.

Lemma 1

The money burning function b(t) is differentiable almost everywhere on [0, 1].

The proof of Proposition 1 is constructive. We distinguish between finite and infinite partitions.

(A) Finite partitions

Let the number N of pooling intervals $( A_{i},B_{i} )\in P_{\mathrm {0}}$ be finite. For the sake of convenience, we index intervals in the order of their positions, i.e., $B_{i-1}\le A_{i}<B_{i}\le A_{i+1}$, for all $i=1,\ldots ,N$, $N{\in \mathbb {N}}$, where $B_{0}{\equiv 0}$ and $A_{N+1}{\equiv 1}$. We construct the equilibrium ${\Omega }_{0}$ in four steps. In step 1, we define Receiver’s beliefs and his best response strategy $\alpha ( m,b )$. In step 2, we use the Sender’s local incentive compatibility conditions to partially determine her best response signaling strategy $\sigma ( t )=( m( t ),b( t ) )$. In step 3, we fully determine $\sigma ( t )$ by preventing global deviations. Finally, in step 4, we choose off-path beliefs.

Step 1.

If $t\in ( A_{i},B_{i} )$, the message of the Sender is $m_{i}^{\mathrm {P}}=$“the state $t\in ( A_{i},B_{i} )$”, and the amount of money burned is $b( t )=b_{i}^{\mathrm {P}}$. The belief of the Receiver is that $t\in ( A_{i},B_{i} )$ and the best response strategy is $\alpha ( m_{i}^{\mathrm {P}},b_{i}^{\mathrm {P}} )=a_{i}$, where $a_{i}$ is an action that maximizes his expected utility:

$$\begin{aligned} a_{i} \equiv \mathop {{\text {argmax}}}\limits _{a} \,E\left[ {u^{{\text {R}}} \left( {a,t} \right) |t \in \left( {A_{i} ,B_{i} } \right) } \right] . \end{aligned}$$

(8)

If $t\in ( B_{i},A_{i+1} )$, the message of the Sender is $m^{\mathrm {S}}( t )=$“the state is t”, and the amount of money burned is $b( t )=b^{\mathrm {S}}( t )$. The belief of the Receiver is that state t equals the reported state, and the best response strategy is $\alpha ( m^{\mathrm {S}}( t ),b^{\mathrm {S}}( t ) )=t$.

Step 2.

If $t\in ( A_{i},B_{i} )$, and the Sender signals $\sigma _{i}^{\mathrm {P}}=( m_{i}^{\mathrm {P}},b_{i}^{\mathrm {P}} )$, she gets utility

$$\begin{aligned} v_{i}^{\mathrm {P}}( t )=u( a_{i},t,x )-b_{i}^{\mathrm {P}}. \end{aligned}$$

(9)

If $t\in ( B_{i},A_{i+1} )$ but the Sender signals as if the state were $z\in ( B_{i},A_{i+1} )$, she gets utility

$$\begin{aligned} v\left( t,z \right) =u\left( z,t,x \right) -b^{\mathrm {S}}\left( z \right) . \end{aligned}$$

In $\Omega _{{0}}$, a necessary truth-telling condition is that v(t, z) attains its maximum at $z=t$. As $b^{\mathrm {S}}( z )$ is differentiable by Lemma 1, the first-order condition $0=\frac{\partial v}{\partial z}$ at $z=t$ yields:

$$\begin{aligned} b^{\mathrm {S}}\left( t \right) =\int _{B_{i}}^t {u_{a}\left( z,z,x \right) dz} +b_{i}^{\mathrm {S}}, \end{aligned}$$

(10)

where $b_{i}^{\mathrm {S}}$ is a constant of integration, yet to be determined.

Thus, if $t\in ( B_{i},A_{i+1} )$, and the Sender signals $\sigma ^{\mathrm {S}}( t )=( m^{\mathrm {S}}( t ),b^{\mathrm {S}}( t ) )$ she gets utility

$$\begin{aligned} v^{\mathrm {S}}\left( t \right) =u\left( t,t,x \right) -b^{\mathrm {S}}\left( t \right) =u\left( t,t,x \right) -\int _{B_{i}}^t {u_{a}\left( z,z,x \right) dz} -b_{i}^{\mathrm {S}}. \end{aligned}$$

(11)

Step 3.

To prevent global deviations it must necessarily be that $v_{i}^{\mathrm {P}}( A_{i} )=v^{\mathrm {S}}( A_{i} )$ and $v_{i}^{\mathrm {P}}( B_{i} )=v^{\mathrm {S}}( B_{i} )$. These two equalities imply:

$$\begin{aligned} \left\{ {\begin{array}{l} b_{i}^{\mathrm {S}}=u\left( B_{i},B_{i},x \right) -u\left( a_{i},B_{i},x \right) +b_{i}^{\mathrm {P}} \\ b_{i+1}^{\mathrm {P}}=u\left( a_{i+1},A_{i+1},x \right) -u\left( A_{i+1},A_{i+1},x \right) +\displaystyle \int _{B_{i}}^{A_{i+1}} {u_{a}\left( t,t,x \right) dt} +b_{i}^{\mathrm {S}} \\ \end{array}} \right. \end{aligned}$$

(12)

Thus, constants $b_{i}^{\mathrm {P}}$ and $b_{i}^{\mathrm {S}}$ are linearly dependent. Since the number of equations is one less than the number of the constants, one of the constants, e.g., $b_{1}^{\mathrm {P}}$, can be chosen freely, and the others will follow from (12).

We need to ensure that the amounts of money burned in each state are non-negative, and that there is a state in which no money is burned. We define ${\Delta }_{i}^{\mathrm {P}}$, ${\Delta }_{i}^{\mathrm {S}}$, and $\tilde{b}$ as follows:

$$\begin{aligned} {\Delta }_{i}^{\mathrm {P}}\equiv & {} b_{i}^{\mathrm {P}}-b_{1}^{\mathrm {P}},\, {\Delta }_{i}^{\mathrm {S}}\equiv \left\{ {\begin{array}{ll} b_{i}^{\mathrm {S}}-b_{1}^{\mathrm {P}}, &{}\quad if\, \, B_{i}<A_{i+1} \\ 0, &{}\quad if\, \, B_{i}=A_{i+1} \\ \end{array}} \right. \nonumber \\ \tilde{b}\equiv & {} \mathrm{inf}_{i}\left( \min \left\{ {\Delta }_{i}^{\mathrm {P}},{\Delta }_{i}^{\mathrm {S}} \right\} \right) \le 0 \end{aligned}$$

(13)

The last inequality follows from ${\Delta }_{1}^{\mathrm {P}}=0$. In other words, ${\Delta }_{i}^{\mathrm {P}}$ is the difference between money burned in intervals i and 1. Likewise, for separating intervals ${\Delta }_{i}^{\mathrm {S}}$ is the difference between money burned in the separating state $t=B_{i}$ and in the first pooling interval 1. It follows from (12) that ${\Delta }_{i}^{\mathrm {P}}$ and ${\Delta }_{i}^{\mathrm {S}}$ are fully determined by marginal types $\{ A_{i} \}$ and $\{ B_{i} \}$. Finally, when $b_{1}^{\mathrm {P}}$ is set to zero, $b_{1}^{\mathrm {P}}=0$, $\tilde{b}$ is the lowest of $b_{i}^{\mathrm {P}}$ and $b_{i}^{\mathrm {S}}$ by construction. It is easy to see that by taking $b_{1}^{\mathrm {P}}=-\tilde{b}$, we ensure that (i) all $b_{i}^{\mathrm {P}}$ and $b_{i}^{\mathrm {S}}$ are non-negative, and (ii) at least one $b_{i}^{\mathrm {P}}$ or $b_{i}^{\mathrm {S}}$ is zero due to finite N. We denote this strategy profile by ${\Omega }_{\mathrm {0}}=( \sigma _{0},\alpha _{\mathrm {0}} )$, and a state in which no money is burned by $t_{0}$: if $b_{i}^{\mathrm {S}}=0$ then $t_{0}=B_{i}$, and if $b_{i}^{\mathrm {P}}=0$ then we take any $t_{0}\in ( A_{i},B_{i} )$.

In order to check that the Sender does not want to deviate globally, we note that

$$\begin{aligned} \frac{d}{dt}v_{i}^{\mathrm {P}}\left( A_{i} \right) >\frac{d}{dt}v^{\mathrm {S}}\left( A_{i} \right) \quad \hbox { and }\quad \frac{d}{dt}v_{i}^{\mathrm {P}}\left( B_{i} \right) <\frac{d}{dt}v^{\mathrm {S}}\left( B_{i} \right) . \end{aligned}$$

Together with $v_{i}^{\mathrm {P}}( A_{i} )=v^{\mathrm {S}}( A_{i} )$ and $v_{i}^{\mathrm {P}}( B_{i} )=v^{\mathrm {S}}( B_{i} )$, this implies that for any $t\in ( A_{i},B_{i} )$, the Sender strictly prefers to pool with $\sigma _{i}^{\mathrm {P}}$ rather than to signal $\sigma _{i-1}^{\mathrm {S}}$ just below $A_{i}$ or to signal $\sigma _{i}^{\mathrm {S}}$ just above $B_{i}$. Due to the assumed single-crossing property $u_{at}>0$, she never prefers to deviate if the state is even further away from $( A_{i},B_{i} )$. Similarly, for any $t\in ( B_{i},A_{i+1} )$, the Sender strictly prefers to signal $t=B_{i}$ rather than to signal just below it, and strictly prefers to signal $t=A_{i+1}$ rather than to signal just above it. Due to the single-crossing property, neither does she have a profitable deviation further away from $( B_{i},A_{i+1} )$. Thus, the utility of the Sender v(t, z) in state t who signals as if she had observed state z,

$$\begin{aligned} v\left( t,z \right) =\left\{ {\begin{array}{ll} u\left( a_{i},t,x \right) -b_{i}^{\mathrm {P}}, &{}\quad if\, z\in \left( A_{i},B_{i} \right) \\ u\left( z,t,x \right) -b^{\mathrm {S}}\left( z \right) ,&{}\quad if\, z\in S^{\mathrm {S}} \\ \end{array}} \right. \end{aligned}$$

(14)

where $b_{i}^{\mathrm {P}}$ and $b^{\mathrm {S}}( z )$ are characterized above, satisfies the global incentive compatibility constrains $v( t,t )\ge v( t,z )$ for $t,z\in [ 0,1 ]$.

Step 4.

By construction, there is a state $t=t_{0}$ in which the Sender burns no money. If this state is a lower bound of a separating interval, i.e., $t_{0}=B_{i}<A_{i+1}$, the off-path beliefs for any off-path signal $\sigma ^{\mathrm{OFF}}$ can be that the Sender signals $\sigma ^{\mathrm{OFF}}$ only in state $t=t_{0}$. If, to the contrary, it is an interior point of a pooling interval, i.e., $t_{0}\in ( A_{i},B_{i} )$, the off-path beliefs can be that only for states $t\in ( A_{i},B_{i} )$ she sends off-path signals. Then, all the equilibrium conditions will be satisfied.

(B) Infinite partitions

Let the number of pooling intervals $( A_{i},B_{i} )\in P_{0}$ be infinite. We order the intervals in $P_{0}$ by their lengths, $D_{i}=B_{i}-A_{i}$, i.e., $D_{i}\ge D_{i+1}$ for all $i=1,\ldots \infty$. In other words, we let interval $( A_{1},B_{1} )$ be the longest, then the second-longest interval $( A_{2},B_{2} )$ follows, etc.

Let us consider a sequence of partitions $\{ P^{( k )} \}$, $k=1,\, \ldots \infty$, where $P^{( k )}$ consists of k longest intervals from $P_{\mathrm {0}}$:

$$\begin{aligned} P^{\left( k \right) }=\left\{ \left( A_{i},B_{i} \right) ,i=1,\ldots ,k \right\} . \end{aligned}$$

In what follows we use the superscript (k) to refer to variables corresponding to the partition $P^{( k )}$, and omit the superscript when we refer to the limiting partition $P_{\mathrm {0}}$, which is considered as a limit of $P^{( k )}$ when $k\rightarrow \infty$. For each finite k, we construct a strategy profile $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ as described above in step 3 for finite partitions, and denote the utility function (14) in $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ by $v^{( k )}( t,z )$.

In step 1 below, we show that the limiting strategy profile $( \tilde{\sigma },\tilde{\alpha } )$ is well defined. In step 2, we show that a necessary condition for $( \tilde{\sigma },\tilde{\alpha } )$ to be an equilibrium strategy profile holds for all on-path signals. In step 3, we show that in $( \tilde{\sigma },\tilde{\alpha } )$, there always exists a state $t_{0}$ in which no money is burned. By choosing off-path beliefs as in step 4 for finite partitions, we turn $( \tilde{\sigma },\tilde{\alpha } )$ into an equilibrium strategy profile ${\Omega }_{\mathrm {0}}$ with infinitely many pooling intervals.

Step 1.

By construction, in marginal states $t\in \bigcup _{i=1}^k \{ A_{i},B_{i} \}$ of a finite partition $P^{( k )}$, the Sender has multiple best responses, and we assume that she separates when she is indifferent between separating and pooling with other states. As a result, for any finite partition $P^{( k )}$, the set $S^{\mathrm {P}}$ of all states in which the Sender pools in $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ is open. In an infinite partition $P_{0}$, $S^{\mathrm {P}}$ is a union of open sets and, therefore, is also open, and $S^{\mathrm {S}}$ is closed.

Consider a state $t\in [ 0,1 ]$. If $t\in S^{\mathrm {P}}$ in $P_{0}$ so that t pools, then $t\in ( A_{i},B_{i} )$ for some i. In this case, $m( t )=m_{i}^{\mathrm {P}}$ (defined in step 1 for finite partitions) in all $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ for $k\ge i$, so that $m^{( k )}( t )$ converges to $m_{i}^{\mathrm {P}}$. If $t\in S^{\mathrm {S}}$ in $P_{0}$ so that t separates, then $m( t )=m^{\mathrm {S}}( t )$ (defined in step 1 for finite partitions) for all k. Thus, for any t, $m^{( k )}( t )$ is eventually constant and converges to a well defined m(t).

To show that $b^{( k )}( t )$ also converges to its limit b(t), we consider two strategy profiles $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ and $( \tilde{\sigma },\tilde{\alpha } )^{( k+1 )}$. Partition $P^{( k+1 )}$ has one extra interval of length $D_{k+1}$:

$$\begin{aligned} P^{\left( k+1 \right) }=P^{\left( k \right) }\cup \left\{ \left( A_{k+1},B_{k+1} \right) \right\} . \end{aligned}$$

We define the difference

$$\begin{aligned} d_{k+1}\left( t \right) \equiv b^{\left( k+1 \right) }\left( t \right) -b^{\left( k \right) }\left( t \right) , \end{aligned}$$

so that we can write $b^{( k+1 )}=b^{( 1 )}+\sum _{2\le i\le k+1} d_{i}$. We will show that $| d_{k} |\le Q\cdot D_{k}$ for some constant Q and, therefore,

$$\begin{aligned} \sum \limits _{2\le i\le k+1} \left| d_{i} \right| \le Q\sum \limits _{2\le i\le k+1} \left| D_{i} \right| \le Q, \end{aligned}$$

so that $b^{( k )}( t )$ converges uniformly to its limit b(t), by the Weierstrass M-test.

Let the pooling interval $( A_{k+1},B_{k+1} )\in P^{( k+1 )}$ be inserted after an interval $( A_{i},B_{i} )\in P^{( k )}$, i.e., $( A_{k+1},B_{k+1} )\mathbf \,{\subset }\,( B_{i}^{( k )},A_{i+1}^{( k )} )$, and be denoted by $( A_{i+1}^{( k+1 )},B_{i+1}^{( k+1 )} )$. Hence,

$$\begin{aligned} B_{i}^{\left( k \right) }=B_{i}^{\left( k+1 \right) }\le A_{i+1}^{\left( k+1 \right) }<B_{i+1}^{\left( k+1 \right) }\le A_{i+1}^{\left( k \right) }=A_{i+2}^{\left( k+1 \right) }. \end{aligned}$$

For $j\le i$, all $b_{j}^{\mathrm {P}}$ and $b_{j}^{\mathrm {S}}$ are identical in both in $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ and $( \tilde{\sigma },\tilde{\alpha } )^{( k+1 )}$. To the contrary, for $j>i$, $b_{j}^{\mathrm {P}}$ and $b_{j}^{\mathrm {S}}$ will be determined by $b_{i}^{\mathrm {S}}$ and (12). Under the assumed regularity conditions on the state distribution and on the players’ utility functions, variables $b_{j}^{\mathrm {P}}$ and $b_{j}^{\mathrm {S}}$ are continuously differentiable functions of $B_{i+1}^{( k+1 )}$ for $B_{i+1}^{( k+1 )}\in [ A_{i+1}^{( k+1 )},A_{i+2}^{( k+1 )} ]$ and $j>i$. Thus, the amount of money $b^{( k+1 )}( t )$ burned in state t can be written as a continuously differentiable function of $B_{i+1}^{( k+1 )}$, i.e., $b^{( k+1 )}( t )=\tilde{b}^{( k+1 )}( t,B_{i+1}^{( k+1 )} )$. By construction, $\tilde{b}^{( k+1 )}( t,A_{i+1}^{( k+1 )} )=b^{( k )}( t )$. Hence,

$$\begin{aligned} d_{k+1}=b^{\left( k+1 \right) }\left( t \right) -b^{\left( k \right) }\left( t \right) =\tilde{b}^{\left( k+1 \right) }\left( t,B_{i+1}^{\left( k+1 \right) } \right) -\tilde{b}^{\left( k+1 \right) }\left( t,A_{i+1}^{\left( k+1 \right) } \right) , \end{aligned}$$

and, by the Mean Value Theorem, $d_{k+1}=D_{k+1}\frac{\partial \tilde{b}^{( k+1 )}}{\partial B_{i+1}^{( k+1 )}}( t,B )$ for some $B\in \big [ A_{i+1}^{( k+1 )},B_{i+1}^{( k+1 )} \big ]$. Since $\frac{\partial \tilde{b}^{( k+1 )}}{\partial B_{i+1}^{( k+1 )}}( t,B )$ is continuous on $( t,B )\in [ 0,1 ]\times \big [ A_{i+1}^{( k+1 )},B_{i+1}^{( k+1 )} \big ]$, it is bounded, i.e., $\big | \frac{\partial \tilde{b}^{( k+1 )}}{\partial B_{i+1}^{( k+1 )}} \big |\le Q$, so that $| d_{k} |\le Q\cdot D_{k}$. Thus, $b^{( k )}( t )$ converges to b(t) uniformly, so that the limiting strategy $\tilde{\sigma }$ is well defined. The Receiver’s limiting best response $\tilde{\alpha }$ is also well defined for on-path signals: $\tilde{\alpha }( \tilde{\sigma }( t ) )=t$ if $t\in S^{\mathrm {S}}$ and $\alpha ( \tilde{\sigma }( t ) )=a_{i}$ (defined in (8)) if $t\in ( A_{i},B_{i} )$.

Step 2.

For profiles $( \tilde{\sigma },\tilde{\alpha } )^{( k )}$ and $( \tilde{\sigma },\tilde{\alpha } )$, we define Receiver’s actions in state t as

$$\begin{aligned} a^{\left( k \right) }\left( t \right) \equiv \tilde{\alpha }^{\left( k \right) }\big ( \tilde{\sigma }^{\left( k \right) }\left( t \right) \big )\quad \hbox { and }\quad a\left( t \right) \equiv \tilde{\alpha }\left( \tilde{\sigma }\left( t \right) \right) , \hbox { respectively}. \end{aligned}$$

Consider $v^{( k )}( t,z )=u( a^{( k )}( z ),t,x )-b^{( k )}( z )$, and its limit v(t, z) when $k\rightarrow \infty$. Since function u is continuous and $a^{( k )}( z )$ and $b^{( k )}( z )$ converge (step 1), the condition $v^{( k )}( t,t ){\ge }v^{( k )}( t,z )$ also holds in the limit for all t and z. That is, $v( t,t )\ge v( t,z )$.

Step 3.

As in step 3 for finite partitions, we use (13) to set $b_{1}^{\mathrm{P}}=-\tilde{b}$. As a result, $\inf _{t\in [0,1]}b( t )=0$. We now show the existence of a state $t_{0}$ in which no money is burned, i.e., $b( t_{0} )=0$. The proof is by contradiction. Suppose, therefore, that $b( t )>0$ for all $t\in [ 0,1 ]$ in $( \tilde{\sigma },\tilde{\alpha } )$. We will show that this leads to $v( t,t )<v( t,z )$ for some t and z, contradicting $v( t,t )\ge v( t,z )$ for all t and z.

When $b( t )>0$, starting from an arbitrary $t_{1}\in [ 0,1 ]$, we construct an infinite sequence of states $\{ t_{n} \}$ such that $b( t_{n+1} )<\min \big \{ \frac{1}{n+1},b( t_{n} ) \big \}$. The sequence $\{ t_{n} \}$ is bounded and, therefore, has an accumulation point. Let $t^{*}$ be such a point. There are infinitely many members of $\{ t_{n} \}$ in either a left or right neighborhood of $t^{*}$. In what follows we focus on the left neighborhood $( t^{*}-\varepsilon ,t^{*} )$. Very similar arguments hold for the right neighborhood $( t^{*},t^{*}+\varepsilon )$.

From $\{ t_{n} \}$, we construct a strictly increasing subsequence of states $\{ t_{n_{m}} \}$ and denote it by $\{ \hat{t}_{m} \}=\{ t_{n_{m}} \}$. By construction, when $m\rightarrow \infty$, both sequences $\{ \hat{t}_{m} \}$ and $\{ b( \hat{t}_{m} ) \}$ monotonically converge to $t^{*}$ and zero, respectively. We will show that $v( t^{*},t^{*} )<v( t^{*},\hat{t}_{m} )$ for all m large enough, and we have reached the contradiction.

First, state $t^{*}$ must be a separating state. If this were not the case, then $t^{*}\in ( A_{i},B_{i} )$ for some i, and $\hat{t}_{m}$ would eventually be in $( A_{i},B_{i} )$ so that $b( \hat{t}_{m+1} )=b( \hat{t}_{m} )$, contradicting $b( \hat{t}_{m+1} )<b( \hat{t}_{m} )$. Therefore, $t^{*}\in S^{\mathrm {S}}$, $a( t^{*} )=t^{*}$, and $b^{*}\equiv b( t^{*} )>0$.

Second, $a( \hat{t}_{m} )$ must converge to $t^{*}$, when $m\rightarrow \infty$. This is easy to see when the number of pooling states in $\{ \hat{t}_{m} \}$ is finite, because $\hat{t}_{m}$ is eventually a separating state and $a( \hat{t}_{m} )=\hat{t}_{m}$ for all m large enough, and $\hat{t}_{m}$ converges to $t^{*}$. When the number of pooling states in $\{ \hat{t}_{m} \}$ is infinite, we construct a subsequence $\{ \hat{t}_{m_{l}} \}$ that includes all pooling states from $\{ \hat{t}_{m} \}$. For any $l=1,\ldots \infty$, there is an interval $( A_{i_{l}},B_{i_{l}} )$ such that $\hat{t}_{m_{l}}\in ( A_{i_{l}},B_{i_{l}} )$ and $a( \hat{t}_{m_{l}} )=a_{i_{l}}\in ( A_{i_{l}},B_{i_{l}} )$. Since intervals $( A_{i_{l}},B_{i_{l}} )$ and $( A_{i_{l+1}},B_{i_{l+1}} )$ are disjoint,

$$\begin{aligned} A_{i_{l}}<\hat{t}_{m_{l}}<B_{i_{l}}<A_{i_{l+1}}<\hat{t}_{m_{l+1}}<B_{i_{l+1}}<t^{*},\quad \hbox { and }\quad A_{i_{l}}<a_{i_{l}}<B_{i_{l}}<t^{*}. \end{aligned}$$

Therefore, since $\hat{t}_{m_{l}}\rightarrow t^{*}$ when $l\rightarrow \infty$, so do $A_{i_{l}}\rightarrow t^{*}$, $B_{i_{l}}\rightarrow t^{*}$, and $a( \hat{t}_{m_{l}} )\rightarrow t^{*}$. This, in turn, implies that for all m large enough, $a( \hat{t}_{m} )$ is arbitrary close to $\hat{t}_{m}$ irrespective of whether $\hat{t}_{m}$ is a pooling or separating state. Hence, $a( \hat{t}_{m} )\rightarrow t^{*}$.

Third, it must be that $v( t^{*},t^{*} )<v( t^{*},\hat{t}_{m} )$ for all m large enough. To show this, we consider the state $t^{*}$. If the Sender sends signal $\tilde{\sigma }( t^{*} )$, her utility is

$$\begin{aligned} v\big ( t^{*},t^{*} \big )=u\big ( a\big ( t^{*} \big ),t^{*},x \big )-b\big ( t^{*} \big )=u\big ( t^{*},t^{*},x \big )-b^{*}. \end{aligned}$$

If, on the other hand, she deviates by sending signal $\tilde{\sigma }( \hat{t}_{m} )$, she gets:

$$\begin{aligned} v\left( t^{*},\hat{t}_{m} \right) =u\left( a\left( \hat{t}_{m} \right) ,t^{*},x \right) -b\left( \hat{t}_{m} \right) , \end{aligned}$$

But

$$\begin{aligned} \mathop {\lim }\nolimits _{{m \rightarrow \infty }} v\left( {t^{*} ,\hat{t}_{m}} \right) = u\left( {t^{*} ,t^{*} ,x} \right) -\mathop {\lim }\nolimits _{{m \rightarrow \infty }} b\left( {\hat{t}_{m}} \right) = u\left( {t^{*} ,t^{*} ,x} \right) > v\left( {t^{*} ,t^{*}} \right) . \end{aligned}$$

This implies that $v( t^{*},t^{*} )<v( t^{*},\hat{t}_{m} )$ for all m large enough.

Thus, the assumption that $b( t )>0$ for all $t\in [ 0,1 ]$ leads to a contradiction. Thus, there exists a state $t_{0}$ in which no money is burned. By choosing off-path beliefs as in Step 4 for finite partitions, we turn $( \tilde{\sigma },\tilde{\alpha } )$ into an equilibrium ${\Omega }_{\mathrm {0}}$ with infinitely many pooling intervals, which ends the proof. $\square$

Proof of Proposition 2

We prove the proposition in four steps. In step 1, we compute Sender’s utility $v^{{\Omega }}( t )$ in ${\Omega }$ for separating states $t\in ( B,A )$. In step 2, we try to construct an equilibrium ${\Omega }^{\varepsilon }$ which differs from ${\Omega }$ in only two ways: (i) the Sender pools states $t\in ( A-\varepsilon ,A )\subset ( B,A )$, for some small $\varepsilon$, and (ii) she burns different amounts of money in higher states $t\in ( A,1 ]$. We compute utility $v^{{\Omega }^{\varepsilon }}( t )$ of the Sender in ${\Omega }^{\varepsilon }$ for pooling states $t\in ( A-\varepsilon ,A )$, and derive a sufficient condition when this construction is possible for marginally small $\varepsilon$, i.e., when $\varepsilon \rightarrow 0$. If this condition holds, then, in step 3, we show that condition (1) of the proposition implies that the Sender’s ex-ante expected utility satisfies $V^{\mathrm {S}}( {\Omega }^{\varepsilon } )>V^{\mathrm {S}}( {\Omega } )$, so that separating states $t\in ( B,A )$ is sub-optimal.

If the sufficient condition for the construction used in step 2 fails, then, in step 4, we construct an equilibrium ${\Omega }^{\varepsilon }$ differently, again by letting the Sender pool $t\in ( A-\varepsilon ,A )\subset ( B,A )$, for some small $\varepsilon$, but now by letting her burn different amounts in lower states $t\in [ 0,A-\varepsilon )$. Here again, we show that condition (3) of the proposition implies that the Sender’s ex-ante expected utility satisfies $V^{\mathrm {S}}( {\Omega }^{\varepsilon } )>V^{\mathrm {S}}( {\Omega } )$, so that separating states $t\in ( B,A )$ is sub-optimal.

Step 1.

Let ${\Omega }$ be an equilibrium with a partition $P=P( {\Omega } )$, and let $( B,A )\subset S^{\mathrm {S}}$ be an interval of states that the Sender separates. Using (10), we write $b^{\mathrm {S}}( t )=\int _B^t {u_{a}( z,z,x )dz} +b^{\mathrm {S}}( B )$ for $t\in ( B,A )$. In state $t\in ( B,A )$, the Sender gets utility $v^{{\Omega }}( t )$ given by (11):

$$\begin{aligned} v^{{\Omega }}\left( t \right) =u\left( t,t,x \right) -b^{\mathrm {S}}\left( t \right) =u\left( t,t,x \right) -\int _B^t {u_{a}\left( z,z,x \right) dz} -b^{\mathrm {S}}\left( B \right) . \end{aligned}$$

Step 2.

Let us take a small $\varepsilon >0$ so that $A-\varepsilon >B$, and define $\tilde{t}\equiv A-\varepsilon$ for convenience. We consider a partition $P^{\varepsilon }=P( {\Omega } )\cup \{ ( \tilde{t},A ) \}$ and a corresponding equilibrium ${\Omega }^{\varepsilon }$ in which the Sender pools in states $t\in ( \tilde{t},A )\subset ( B,A )$. We use the superscript $\varepsilon$ for all variables in ${\Omega }^{\varepsilon }$. The optimal action $a^{\varepsilon }$ for the newly pooled states $t\in ( \tilde{t},A )$ is:

$$\begin{aligned} a^{\varepsilon }=\mathrm {E}\left[ t\vert t\in \left( \tilde{t},A \right) \right] = \frac{\int _{\tilde{t}}^{A} {tdF} }{\int _{\tilde{t}}^{A} {dF}}>\tilde{t}. \end{aligned}$$

Sender’s utility in state $t\in ( \tilde{t},A )$ is then $v^{{\Omega }^{\varepsilon }}( t )=u( a^{\varepsilon },t,x )-b^{\mathrm {P,}\varepsilon }$ where $b^{\mathrm {P,}\varepsilon }$ is the amount of money burned in the pooling interval $( \tilde{t},A )$ in ${\Omega }^{\varepsilon }$.

First, we try to construct ${\Omega }^{\varepsilon }$ in such a way that in state $t=\tilde{t}$, the Sender gets equal utility in ${\Omega }$ and ${\Omega }^{\varepsilon }$, i.e., $v^{{\Omega }^{\varepsilon }}( \tilde{t} )=v^{{\Omega }}( \tilde{t} )$. This determines $b^{\mathrm {P,}\varepsilon }$:

$$\begin{aligned} b^{\mathrm {P,}\varepsilon }=u\left( a^{\varepsilon },\tilde{t},x \right) -u\left( \tilde{t},\tilde{t},x \right) +\int _{B}^{\tilde{t}} {u_{a}\left( z,z,x \right) d\mathrm {z}} +b^{\mathrm {S}}\left( B \right) . \end{aligned}$$

Therefore, for $t\in ( \tilde{t},A )$, the utility function $v^{{\Omega }^{\varepsilon }}( t )$ is:

$$\begin{aligned} v^{{\Omega }^{\varepsilon }}\left( t \right) =u\left( a^{\varepsilon },t,x \right) -u\left( a^{\varepsilon },\tilde{t},x \right) +u\left( \tilde{t},\tilde{t},x \right) -\int _{B}^{\tilde{t}} {u_{a}\left( z,z,x \right) dz} -b^{\mathrm {S}}\left( B \right) . \end{aligned}$$

We define the difference:

$$\begin{aligned} \theta \left( \varepsilon ,t \right) \equiv v^{{\Omega }}\left( t \right) -v^{{\Omega }^{\varepsilon }}\left( t \right) . \end{aligned}$$

By construction, $\theta ( \varepsilon ,\tilde{t} )=0$. Moreover, at $t=\tilde{t}$:

$$\begin{aligned} \frac{\partial \theta }{\partial t}\left( \varepsilon ,\tilde{t} \right) =u_{t}\left( \tilde{t},\tilde{t},x \right) -u_{t}\left( a\left( \varepsilon \right) ,\tilde{t},x \right) =-\int _{\tilde{t}}^{a^{\varepsilon }} {u_{at}\left( z,\tilde{t},x \right) dz} <0, \end{aligned}$$

due to $u_{at}>0$ and $a^{\varepsilon }>\tilde{t}$. Hence, $v^{{\Omega }^{\varepsilon }}( t )>v^{{\Omega }}( t )$ in some right neighborhood of $\tilde{t}$, see Fig. 1. At $t=A$, the difference in utility $\varphi ( \varepsilon )$, is:

$$\begin{aligned} \varphi \left( \varepsilon \right) \equiv \theta \left( \varepsilon ,A \right) =v^{{\Omega }}\left( A \right) -v^{{\Omega }^{\varepsilon }}\left( A \right) , \end{aligned}$$

can be either positive or negative. Step 3 deals with the case when $\varphi ( \varepsilon )>0$ whereas the case $\varphi ( \varepsilon )\le 0$ is considered in step 4.

Step 3.

If $\varphi ( \varepsilon )>0$, pooling states $t\in ( \tilde{t},A ]$ results in a lower utility of the Sender in state $t=A$. For $P^{\varepsilon }$ to be an equilibrium partition, it suffices that the amount of money that she burns for $t>A$ must be increased by $\varphi ( \varepsilon )$. It can be shown that $\varphi ( 0 )=\varphi {'}( 0 )=\varphi {''}( 0 )=0$ and, finally,

$$\begin{aligned} \varphi '''\left( \mathrm {0} \right) =\frac{\mathrm {1}}{\mathrm {2}}u_{ta}\left( A,A,x \right) \left( {\varPsi } \left( A \right) -\frac{f^{'}\left( A \right) }{f\left( A \right) } \right) . \end{aligned}$$

Hence, if $0<{\varPsi } -\frac{f^{'}}{f}$ at $t=A$, there is an $\overline{\varepsilon }>$0 such that $\varphi ( \varepsilon )>0$ for all $\varepsilon \in ( 0,\overline{\varepsilon })$. The net ex-ante expected utility gain $g( \varepsilon )\equiv \mathrm {E}[ v^{{\Omega }^{\varepsilon }}( t )-v^{{\Omega }}( t ) ]$ from pooling states $t\in ( \tilde{t},A )$ is:

$$\begin{aligned} g\left( \varepsilon \right) =\int _{\tilde{t}}^{A} {\left( v^{{\Omega }^{\varepsilon }}\left( t \right) -v^{{\Omega }}\left( t \right) \right) dF} +\left( v^{{\Omega }^{\varepsilon }}\left( A \right) -v^{{\Omega }}\left( A \right) \right) \left( 1-F\left( A \right) \right) . \end{aligned}$$

It can be shown that $g( 0 )=g{'}( 0 )=g{''}( 0 )=0$, and, finally,

$$\begin{aligned} g^{\prime \prime \prime }\left( 0 \right) = - \frac{1}{2}\left( {1 - F} \right) u_{{ta}} \left( {{\varPsi } - \frac{{f^{\prime }}}{f} - \frac{f}{{1 - F}}} \right) , \end{aligned}$$

where all functions are evaluated at state $t=A$. Thus, if $0<{\varPsi } -\frac{f^{'}}{f}<\frac{f}{1-F}$, the Sender strictly prefers ${\Omega }^{\varepsilon }$ to ${\Omega }$.

Step 4.

If $\varphi ( \varepsilon )<0$, pooling states $t\in ( \tilde{t},A )$ results in a higher utility of the Sender in state $t=A$. For $P^{\varepsilon }$ to be an equilibrium partition, the amounts of money that the Sender burns in all states $t>A$ must be decreased by $-\varphi ( \varepsilon )\ge 0$. Since this is not always feasible (if, e.g., in some states $t>A$, no money is burned in ${\Omega })$, we now require that in all lower states $t<\tilde{t}$, the Sender burns an extra amount of money $-\varphi ( \varepsilon )\ge 0$ relative to what she burns in ${\Omega }$. It can then be shown that when $-\frac{f}{F}<{\varPsi } -\frac{f^{'}}{f}<0$, the Sender strictly prefers ${\Omega }^{\varepsilon }$ to ${\Omega }$.

The only special case left is when ${\varPsi } =\frac{f^{'}}{f}$. When ${\varPsi } =\frac{f^{'}}{f}$, whether $\varphi ( \varepsilon )\ge 0$ or $\varphi ( \varepsilon )\le 0$ is determined by higher-order derivatives. Nevertheless, one of these inequalities will hold and, therefore, condition (1) is the sufficient condition for this special case. $\square$

Proof of Corollary 1

The feasibility of a separating equilibrium follows from Proposition 1. We prove its sub-optimality by contradiction. Suppose that a separating equilibrium is Sender-optimal. Then, condition (1) must fail in all states, i.e., for any $t\in ( 0,\,1 )$ either

$$\begin{aligned}&\left( {\varPsi } \left( t \right) -\frac{f^{'}\left( t \right) }{f\left( t \right) } \right) F\left( t \right) {\le -}f\left( t \right) ,\quad \hbox { or} \end{aligned}$$

(15)

$$\begin{aligned}&\left( {\varPsi } \left( t \right) -\frac{f^{'}\left( t \right) }{f\left( t \right) } \right) \left( 1-F\left( t \right) \right) {\ge }f\left( t \right) \end{aligned}$$

(16)

holds. At $t=0$, condition (15) fails so that, by continuity, it also fails to hold for t close to zero. Thus, condition (16) must hold, i.e., $( {\varPsi } ( 0 )-\frac{f^{'}( 0 )}{f( 0 )} ){\ge }f( 0 )>0$. On the other hand, at $t=1$, condition (16) fails so that condition (15) must hold, i.e., $( {\varPsi } ( 1 )-\frac{f^{'}( 1 )}{f( 1 )} ){\le -}f( 1 )<0$. As ${\varPsi } -\frac{f^{'}}{f}$ is continuous, there exists a state $\hat{t}\in ( 0,1 )$ at which ${\varPsi } -\frac{f^{'}}{f}=0$. This implies that (3) holds at $t=\hat{t}$, a contradiction. Hence, condition (3) must necessarily hold for some $t\in ( 0,\,1 )$ and complete separation is sub-optimal. $\square$

Proof of Corollary 2

The left-hand side and right-hand side of (3) can be written as follows:

$$\begin{aligned} LHS=-\frac{f\left( t \right) }{F\left( t \right) }+\frac{f^{'}\left( t \right) }{f\left( t \right) }=\frac{\lambda ^{'}\left( t \right) }{\lambda \left( t \right) }\quad \hbox { and }\quad RHS=\frac{f\left( t \right) }{1-F\left( t \right) }+\frac{f^{'}\left( t \right) }{f\left( t \right) }=\frac{r^{'}\left( t \right) }{r\left( t \right) }, \end{aligned}$$

where $r( t )=\frac{f( t )}{1-F( t )}$ is the hazard rate, and $\lambda ( t )\equiv \frac{f( t )}{F( t )}$ is the reversed hazard rate. The log-concave density implies both an increasing hazard rate, $r^{'}( t )>0$, and a decreasing reversed hazard rate, $\lambda ^{'}( t )<0$, see, e.g., Bagnoli and Bergstrom (2005). Moreover, as ${\varPsi } ( t )=0$ for the quadratic loss function, the result follows. $\square$

Proof of Proposition 3

In this proof, we use the following lemma, proven in Appendix B. $\square$

Lemma 2

The optimal number of pooling intervals is finite, i.e., $N^{{*}}<\infty$.

In the proof of Lemma 2 we show that if an equilibrium ${\Omega }$ had infinitely many pooling intervals, then there must have been infinitely many infinitely small intervals located infinitely close to each other in the state space. By pooling some of those intervals, we construct another equilibrium which yields a higher expected utility to the Sender.

According to Proposition 1, Corollary 2, and Lemma 2, we can search for an optimal equilibrium by searching through the set of finite partitions P consisting of pooling intervals only, $B_{i}=A_{i+1}$. We prove the proposition in 2 steps. In step 1, we derive the optimization problem (4) and (5) that ${\Omega }^{{*}}$ should solve. In step 2, we show that this problem always has a solution.

Step 1.

Derivations here replicate a large part of the derivations used in the proof of Lemma 2. We write $B_{i}=A_{i+1}$, $a_{i}=\frac{1}{2}( A_{i}+A_{i+1} )$, and the pooling utility function of the Sender (9) as:

$$\begin{aligned} v_{i}^{\mathrm {P}}\left( t \right) =-\left( t+x-\frac{1}{2}\left( A_{i+1}+A_{i} \right) \right) ^{2}-b_{i}^{\mathrm {P}}. \end{aligned}$$

Using $v_{i}^{\mathrm {P}}( A_{i} )=v_{i+1}^{\mathrm {P}}( A_{i} )$, it can be shown that the following expression

$$\begin{aligned} \frac{\mathrm {1}}{\mathrm {4}}\left( A_{i+1}-A_{i} \right) ^{2}-\left( A_{i+1}+A_{i} \right) x+b_{i}^{\mathrm {P}} \end{aligned}$$

is independent of i. We denote this constant by c, which allows us to write $b_{i}^{\mathrm {P}}=c^{\mathrm {P}}( A_{i},A_{i+1},c )$ for all $i=1,\ldots ,N$, where

$$\begin{aligned} c^{\mathrm {P}}\left( A_{i},A_{i+1},c \right) \equiv \left( A_{i+1}+A_{i} \right) x-\frac{\mathrm {1}}{\mathrm {4}}\left( A_{i+1}-A_{i} \right) ^{2}+c. \end{aligned}$$

Then, we write $v^{\mathrm {P}}( t )$ as follows:

$$\begin{aligned} v^{\mathrm {P}}\left( t \right) =-x^{2}-2tx+\left( A_{i+1}-t \right) \left( t-A_{i} \right) -c, \end{aligned}$$

Integrating $v^{{\Omega }}( t )$ over $t\in [ 0,\,1 ]$ yields ex-ante expected utility of the Sender $V^{\mathrm {S}}$ given in (4), and (5) is just a non-negativity condition $b_{i}^{\mathrm {P}}\ge 0$.

Step 2.

The set of partitions of at most N intervals is compact (it is defined by $A_{i}\le A_{i+1}$ for $i\le N$, $A_{1}=0$, $A_{N+1}=1$). In addition, we can restrict the values of c by $c\in \big [ -2x,\frac{\mathrm {1}}{\mathrm {4}} \big ]$. Indeed, taking $c<-\mathrm {2}x$ is not feasible as this would violate $c^{\mathrm {P}}( A,B,c )\ge 0$, and taking $c>\frac{\mathrm {1}}{\mathrm {4}}$ is not optimal since in this case $c^{\mathrm {P}}( A,B,c )>0$ and $V^{\mathrm {S}}$ decreases in c. Finally, $V^{\mathrm {S}}$ is continuous. Thus, equilibrium ${\Omega }^{{*}}$ exists.$\square$

Proof of Proposition 4

In this proof, we use the following lemma, proven in Appendix B.

Lemma 3

If the Sender burns money in an optimal equilibrium ${\Omega }^{{*}}$, she does so in the second interval only, i.e., if $b_{i}^{\mathrm {P}}>0$ then $i=2$.

In the proof of Lemma 3 we show first that if money is burned in two or more intervals, this equilibrium is suboptimal. Then we show that burning money in interval $i\ge 3$ is also suboptimal. Finally, we show the sub-optimality of equilibria where money is burned in the first interval. In all three statements, we show the sub-optimality of equilibria by constructing other equilibria that are better from the Sender’s perspective.

According to Lemma 3, $b_{1}^{\mathrm {P}}=0$ and $b_{i}^{\mathrm {P}}=0$ for $i=3,\ldots ,n$. Hence, $A_{2}\in ( 0,1 ]$ implicitly defines c by $c^{\mathrm {P}}( 0,A_{2},c )=0$:

$$\begin{aligned} c\left( A_{2} \right) =\frac{1}{4}A_{2}^{2}-xA_{2}, \end{aligned}$$

Moreover, equalities $b_{i}^{\mathrm {P}}=0$ for $i=3,\ldots ,n$, define $A_{i}( A_{i+1} )$ implicitly and recursively by $c^{\mathrm {P}}( A_{i},A_{i+1},c )=0$. It can be shown by induction that all marginal states $A_{i}$, $i=3,\ldots ,n$, can be written as the following function of $A_{2}$:

$$\begin{aligned} A_{i}\left( A_{2} \right) =1-2\left( n-i+1 \right) \left( s\left( A_{2} \right) -\left( n-i+1 \right) x \right) , \end{aligned}$$

where

$$\begin{aligned} s\left( A_{2} \right) =\sqrt{x^{2}+2x+c\left( A_{2} \right) } =\frac{1}{2}\sqrt{\left( 2x-A_{2} \right) ^{2}+8x}. \end{aligned}$$

Thus, choosing $A_{2}\in ( 0,1 ]$ completely determines all other marginal states $A_{i}( A_{2} )$. That is why we can consider Sender’s utility $V^{\mathrm {S}}=V^{\mathrm {S}}( {\Omega } )$ as a function of $A_{2}$, and write it as $V^{\mathrm {S}}( A_{2} )$, abusing notation slightly.

We prove the proposition in 4 steps. In step 1, we fix the number of intervals in the partition, n, and show that $A_{2}$ must satisfy a restriction $A_{2}\in [ \underline{A}_{2},\overline{A}_{2} )$. In step 2, we derive $G( A_{2} )\equiv \frac{dV^{\mathrm {S}}}{dA_{2}}$ and argue that in an optimal equilibrium ${\Omega }^{{*}}$, either $A_{2}\in ( \underline{A}_{2},\overline{A} _{2} )$ and $G( A_{2} )=0$ (interior maximum), or $A_{2}=\underline{A}_{2}$ (corner maximum). In step 3, we argue that if x is just below $x_{N}$, the optimal number $N^{*}$ of intervals is $N^{*}=N$, and the maximum is in the interior. This proves part (a) of the proposition. In step 4, we argue that if x is just above $x_{N}$, the optimal number of intervals is $N^{*}=N+1$, and the maximum is in the interior. This proves part (b).

Step 1.

By choosing $A_{\mathrm {2}}\in ( \mathrm {0,1} ]$, marginal state $A_{3}$ is $A_{3}( A_{2} )=1-2( n-2 )( s( A_{2} )-( n-2 )x )$, and the amount of money burned in the second interval is $b_{2}^{\mathrm {P}}( A_{2} )=c^{\mathrm {P}}( A_{2},A_{3}( A_{2} ),c( A_{2} ) )$. There are two conditions, namely $A_{3}( A_{2} )>A_{2}$ and $b_{2}^{\mathrm {P}}( A_{2} )\ge 0$, that have to hold in ${\Omega }$. These conditions imply $A_{2}<\overline{A}_{2}$ and $A_{2}\ge \underline{A}_{2}$, respectively, where

$$\begin{aligned} \underline{A}_{2}\equiv 2\left( n-1 \right) \left( x_{n}-x \right) \quad \hbox { and }\quad \overline{A}_{2}\equiv 2\left( n-2 \right) \left( x_{n-1}-x \right) . \end{aligned}$$

Step 2.

Using the above expressions for $A_{i}( A_{2} )$ and $c( A_{2} )$, we write $V^{\mathrm {S}}$ as follows:

$$\begin{aligned} V^{\mathrm {S}}=-x^{2}-x+\frac{1}{6}\left( A_{2}^{3}+\left( A_{3}-A_{2}\right) ^{3}+4x\left( 1-A_{3}^{2} \right) -2\left( 1+2A_{3} \right) \left( \frac{1}{4}A_{2}-x \right) A_{2} \right) , \end{aligned}$$

and its derivative $G( A_{2} )\equiv \frac{dV^{\mathrm {S}}}{dA_{2}}$ as:

$$\begin{aligned} G= & {} \frac{1}{6}\bigg ( A_{3}\left( 4\left( A_{2}+x \right) -3A_{3} \right) -A_{2}+2x \\&+\left( 3\left( A_{3}-A_{2} \right) ^{2}{-A_{2}}^{2}-4x\left( 2A_{3}-A_{2} \right) \right) \frac{dA_{3}}{dA_{2}} \bigg ), \end{aligned}$$

where $\frac{dA_{3}}{dA_{2}}=\frac{1}{2s}( N-2 )( 2x-A_{2} )$.

In ${\Omega }^{{*}}$, $V^{\mathrm {S}}$ must attain its maximum over $A_{2}\in [ \underline{A}_{2},\overline{A}_{2} )$. If, on the one hand, it happens at the corner $A_{2}=\underline{A}_{2}$, then $b_{2}^{\mathrm {P}}=0$ and the resulting equilibrium is the cheap talk equilibrium with n intervals. If, on the other hand, the maximum is in the interior at $A_{2}=A_{2}^{{*}}\in ( \underline{A}_{2},\overline{A} _{2} )$, it implies that $V^{\mathrm {S}}( A_{2}^{{*}} )>V^{\mathrm {S}}( \underline{A}_{2} )$ and, therefore, ${\Omega }^{{*}}$ yields a strictly higher utility level to the Sender than the cheap talk equilibrium with n intervals. In this case, the first-order condition is $G( A_{2}^{{*}} )=0$.

Step 3.

Let $N\ge 3$. We define $\hat{x}_{N}\in ( x_{N+1},x_{N} )$ as follows:

$$\begin{aligned} \hat{x}_{N}\equiv \frac{\mathrm {1}}{\mathrm {2}N^{\mathrm {2}}}. \end{aligned}$$

Suppose $x\in [ x_{N+1},x_{N} )$, such that the most informative cheap talk equilibrium ${\Omega }^{\mathrm {CT}}$ has a partition $P( {\Omega }^{\mathrm {CT}} )$ with N intervals of strictly positive lengths. Note that, $\overline{A}_{2}>A_{2}$ implies $x_{n-1}>x$, which together with $x\ge x_{N+1}$ implies $x_{n-1}>x_{N+1}$. This yields $n\le N+1$. Thus, the optimal equilibrium ${\Omega }^{{*}}$ has at most $N+1$ intervals, i.e., $N^{*}\le N+1$. Let $x\in [ \hat{x}_{N},x_{N} )$ and distinguish three cases.

Suppose, first, $n=N+1\ge 4$. Then, $x\in [ \hat{x}_{n-1},x_{n-1} )$, $x>\hat{x}_{n-1}>x_{n}$ and $\underline{A}_{\mathrm {2}}<$ so that $A_{\mathrm {2}}$ satisfies $A_{\mathrm {2}}\in [ \mathrm {0,}\overline{A} _{\mathrm {2}} )$. It can be shown that $G( A_{\mathrm {2}} )>$ for all $A_{\mathrm {2}}\in [ \mathrm {0,}\overline{A}_{\mathrm {2}} )$. Hence, $V^{\mathrm {S}}$ monotonically increases up to $A_{\mathrm {2}}=\overline{A} _{\mathrm {2}}$, which is the cheap talk equilibrium with $n=N$ intervals, ${\Omega }^{\mathrm {CT}}$. Thus, $n=N+1$ is not optimal, and it must be that $n\le N$.

Suppose, second, $n=N\ge \mathrm {3}$. Then, $x\in [ \hat{x}_{n},x_{n} )$, and $A_{2}\in [ \underline{A}_{2},\overline{A}_{2} )$. It can be shown that $G( \underline{A}_{2} )>0>G( \overline{A}_{2} )$ at $x=x_{N}$ and $G( \underline{A}_{2} )<0$ at $x=\hat{x}_{N}$. By continuity, there exists a $\underline{y}_{N}\in ( \hat{x}_{N},x_{N} )$ such that $G( \underline{A}_{2} )>0>G( \overline{A}_{2} )$ for all $x\in ( \underline{y}_{N},x_{N} ]$. This implies, that there exists $A_{2}^{{*}}\in ( \underline{A}_{2},\overline{A}_{2} )$ which is a local maximum of $V^{\mathrm {S}}$, and at which $b_{2}^{P}>0$. We note that $V^{\mathrm {S}}( A_{2}^{{*}} )>V^{\mathrm {S}}( \underline{A}_{2} )$, where $V^{\mathrm {S}}( \underline{A}_{2} )$ is the Sender’s utility in ${\Omega }^{\mathrm {CT}}$. Thus, for $x\in (\underline{y}_{N},x_{N} ]$, equilibrium with $n=N$ and $A_{\mathrm {2}}=A_{2}^{{*}}$ is better for the Sender than ${\Omega }^{\mathrm {CT}}$ with N intervals.

Third, suppose $n\le N-1$. In this case, ${x<x}_{n+1}$. It can be shown that $G( A_{2} )<0$ for all $A_{2}\in [ \underline{A}_{2},\overline{A}_{2} )$. Hence, $V^{\mathrm {S}}$ monotonically decreases and achieves its maximum at $A_{2}=\underline{A}_{2}$, the cheap talk equilibrium with $n\le N-1$ intervals. Thus, all equilibria with $n\le N-1$ are dominated by ${\Omega }^{\mathrm {CT}}$ and, therefore, are not optimal.

Combining the above three cases, we conclude that if $x\in (\underline{y}_{N},x_{N} ]$, the maximum is in the interior, $A_{2}^{{*}}\in ( \underline{A}_{2},\overline{A}_{2} )$, and the number of intervals is $N^{{*}}=N$.

Step 4.

Let $x\in [ x_{N+1},\hat{x}_{N} )$. As in step 3, we consider tree cases.

Suppose, first, that $n=N+1\ge 4$. Then, $x\in [ x_{n},\hat{x}_{n-1} )$, so that $\underline{A}_{\mathrm {2}}{\le 0}$ and $A_{2}\in [ 0,\,\overline{A}_{2} )$. It can be shown that $G( 0 )>0>G( \overline{A}_{\mathrm {2}} )$ at $x=x_{N+1}$ and that $G( \overline{A}_{\mathrm {2}} )>0$ at $x=\hat{x}_{N}$. By continuity, there exists a $\overline{y}_{N+1}\in ( x_{N+1},\hat{x}_{N} )$ such that $G( \mathrm {0} )>0>G( \overline{A}_{\mathrm {2}} )$ for all $x\in [ x_{N+1},\overline{y} _{N+1} )$. Hence, there exists $A_{\mathrm {2}}^{{*}}\in ( \mathrm {0,}\overline{A}_{\mathrm {2}} )$ which is a local maximum of $V^{\mathrm {S}}$, and at which $b_{\mathrm {2}}^{P}>$. We note that $V^{\mathrm {S}}( A_{2}^{{*}} )>V^{\mathrm {S}}( \overline{A} _{\mathrm {2}} )$, where $V^{\mathrm {S}}( \overline{A} _{\mathrm {2}} )$ is the Sender’s utility in ${\Omega }^{\mathrm {CT}}$. Thus, for $x\in [ x_{N+1},\overline{y}_{N+1} )$, equilibrium with $n=N+1$ and $A_{\mathrm {2}}=A_{2}^{{*}}$ is better for the Sender than ${\Omega }^{\mathrm {CT}}$ with N intervals.

Suppose, second, that $n\le N$. In this case, $x<x_{n}$. It can be shown that $G( A_{2} )<0$ for all $A_{2}\in [ \underline{A}_{2},\overline{A}_{2} )$. Hence, $V^{\mathrm {S}}$ monotonically decreases and achieves its maximum at $A_{2}=\underline{A}_{2}$, the cheap talk equilibrium with $n\le N$ intervals. Thus, of all equilibria with $n\le N$ intervals, ${\Omega }^{\mathrm {CT}}$ is the best for the Sender.

Combining the above three cases, we conclude that if $x\in [ x_{N+1},\overline{y}_{N+1} )$, the maximum is in the interior, $A_{2}^{{*}}\in ( \underline{A}_{2},\overline{A}_{2} )$, and the number of intervals is $N^{{*}}=N+1$.$\square$

Remark

Proposition 4 provides a sufficient condition for $b_{2}^{P}>0$. The function $V^{\mathrm {S}}( A_{2} )$ has nice analytical properties, and numerical computations show that it is quasi-concave for all feasible values of $A_{2}$. Therefore, for $x\in ( \overline{y} _{N+1},\underline{y}_{N} )$ and for $x\ge \overline{y} _{4}$, the sufficient condition for burning money, Proposition 4, is also the necessary condition, implying that ${\Omega }^{{*}}={\Omega }^{\mathrm {CT}}$ for all $x\in ( \overline{y} _{N+1},\underline{y}_{N} )$ and for $x\ge \overline{y} _{4}$. That is, no money is burned in the Sender-optimal equilibrium for these values of x.

Proof of Proposition 5

We prove the proposition in 4 steps. In step 1, we show that for this utility specification, all pooling states are convex in any equilibrium. In step 2, we show that when the Sender pools states $t\in ( A,B )$, the optimal action a of the Receiver is $a=A$, the lowest pooling state. In step 3, we show that the money burning function b(t) is weakly increasing in any equilibrium, and that we only need to consider equilibria where $b( 0 )=0$. Finally, in step 4, we show that removing one pooling interval from an equilibrium partition always increases the Sender’s ex-ante utility, so that, by induction, the optimal equilibrium has an empty partition, i.e., is perfectly separating.

Step 1.

For the given function $u^{\mathrm {R}}( a,t )$, the optimal action for the Receiver is $a^{\mathrm {R}}( t )=t$. Hence, even though $u^{\mathrm {R}}( a,t )$ is not differentiable at $a=t$ (not even continuous), Lemma 1 of ASB still holds as it only requires $a^{\mathrm {R}}( t )$ to be strictly increasing, and, therefore, so does our Proposition 1. In other word, all pooling states are convex in any equilibrium.

Step 2.

Let the Receiver get a message sent in a pooling interval (A, B) only. Choosing an action $a\in [ A,B ]$ yields him the following expected utility:

$$\begin{aligned} V^{\mathrm {R}}=\mathrm {E}\left[ u^{\mathrm {R}}\left( a,t \right) \vert t\in \left( A,B \right) \right] =-\frac{1}{B-A}\left( \int _A^B {\left( a-t \right) ^{2}dt} +\gamma \left( a-A \right) \right) . \end{aligned}$$

Differentiating $V^{\mathrm {R}}$ w.r.t. a yields

$$\begin{aligned} \frac{d}{da}V^{\mathrm {R}}=-\frac{1}{B-A}\left( \gamma +\left( a-A \right) ^{2}-\left( a-B \right) ^{2} \right) \le -\frac{1}{B-A}\left( \gamma -1 \right) <0. \end{aligned}$$

Thus, choosing the lowest possible $a=A$ is optimal for the Receiver.

Step 3.

The money burning function b(t) obviously increases on separating states $t\in S^{\mathrm {S}}$ and is constant on each pooling interval $t\in ( A,B )$. Since the Sender in state $t=A$ is indifferent between separating and pooling with states $t\in ( A,B )$, and the Receiver’s action in these two options are also equal, the Sender burns equal amounts of money. Thus, we only need to show that if the Sender in state $t=B$ is indifferent between separating and pooling with states $t\in ( A,B )$, the Sender burns more money if she separates. To this end, we note that when states $t\in ( A,B )$ pool and burn $b^{\mathrm {P}}$, the Sender of type $t=B$ gets utility

$$\begin{aligned} v^{\mathrm {P}}\left( B \right) =u\left( A,B,x \right) -b^{\mathrm {P}}=-\left( B+x-A \right) ^{\mathrm {2}}-b^{\mathrm {P}}, \end{aligned}$$

By separating, she gets

$$\begin{aligned} v^{\mathrm {S}}\left( B \right) =u\left( B,B,x \right) -b^{\mathrm {S}}\left( B \right) . \end{aligned}$$

$v^{\mathrm {P}}( B )=v^{\mathrm {S}}( B )$ implies $b^{\mathrm {S}}( B )-b^{\mathrm {P}}=( B-A )( ( B-A )+2x )>0$. Thus, b(t) is increasing, and $b( t )\ge b( 0 )$. Obviously, $b( 0 )>0$ is not optimal for the Sender as lowering b(t) yields her a higher utility. Thus, we only need to consider equilibria with $b( 0 )=0$.

Step 4.

Let ${\Omega }^{( k )}$ be an equilibrium with a partition $P^{( k )}=P( {\Omega }^{( k )} )$ that contains $k>0$ pooling intervals (k can be infinite here). Let $( A,B )\in P^{( k )}$ so that types $t\in ( A,B )$ pool in ${\Omega }^{( k )}$. Let us consider an equilibrium ${\Omega }^{( k-1 )}$ which partition $P^{( k-1 )}=P( {\Omega }^{( k-1 )} )$ is obtained from $P^{( k )}$ by removing (A, B), i.e., $P^{( k-1 )}=P^{( k-1 )}{\setminus } \!\{ ( A,B ) \}$. In states $t\in [ 0,A ]$, $v^{{\Omega }^{( k )}}( t )=v^{{\Omega }^{( k-1 )}}( t )$. In states $t\in ( A,B )$, the utility functions from pooling (in ${\Omega }^{( k )})$ and separation (in ${\Omega }^{( k-1 )}$) are:

$$\begin{aligned}&v^{\mathrm {P},{\Omega }^{\left( k \right) }}\left( t \right) =u\left( A,t,x \right) -b^{\mathrm {P}}=-\left( t+x-A \right) ^{\mathrm {2}}-b^{\mathrm {P}}, \\&v^{\mathrm {S},{\Omega }^{\left( k-1 \right) }}\left( t \right) =u\left( t,t,x \right) -2x\left( t-A \right) -b^{\mathrm {P}}=-x^{2}-2x\left( t-A \right) -b^{\mathrm {P}}, \end{aligned}$$

and the difference in utility $\varphi ( t )$ is:

$$\begin{aligned} \varphi \left( t \right) \equiv v^{\mathrm {S},{\Omega }^{\left( k-1 \right) }}\left( A \right) -v^{\mathrm {P},{\Omega }^{\left( k \right) }}\left( t \right) =\left( t-A \right) ^{2}>0. \end{aligned}$$

Thus, removing a pooling interval (A, B) from $P^{( k )}$ increases utility of all types $t\in ( A,B )$ by $\varphi ( t )>0$. Since the amount of money that the Sender burns in state $t=B$ in equilibrium ${\Omega }^{( k-1 )}$, which is $2x( B-A )+b^{\mathrm {P}}$, is positive, and b(t) is increasing, the removal does not result in negative values of b(t) for $t>B$.

Moreover, in all states $t>B$, the Sender has to burn $\varphi ( B )=( B-A )^{2}$ less in ${\Omega }^{( k-1 )}$. Thus, the ex-ante expected utility satisfies $V^{{\Omega }^{( k )}}<V^{{\Omega }^{( k-1 )}}$, which ends the proof. $\square$

Appendix B

Proof of Lemma 2

We prove the lemma is 3 steps. In step 1, we derive the ex-ante expected utility of the Sender $V^{\mathrm {S}}( {\Omega } )$ in an equilibrium ${\Omega }$. In step 2, we assume that ${\Omega }$ has infinitely many pooling intervals, and construct another equilibrium ${\Omega }_{\mathrm {1}}$ in which the Sender pools some of the states which she does not pool in ${\Omega }$. In step 3, we show that $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )>V^{\mathrm {S}}( {\Omega } )$, so that the original equilibrium ${\Omega }$ with infinitely many pooling intervals is suboptimal.$\square$

Step 1.

For $f( t )=t$ and $u( a,t,x )=-( a-t-x )^{2}$, the optimal action of the receiver (8), the money-burning function for separated states (10), pooling and separating utility functions (9) and (11) become:

$$\begin{aligned}&a_{i}=\frac{1}{2}\left( B_{i}+A_{i} \right) ,\, b^{\mathrm {S}}\left( t \right) =2xt+\left( b_{i}^{\mathrm {S}}-2xB_{i} \right) \\&v_{i}^{\mathrm {P}}\left( t \right) =-\left( t+x-\frac{1}{2}\left( B_{i}+A_{i} \right) \right) ^{2}-b_{i}^{\mathrm {P}},\quad \hbox { and}\\&v^{\mathrm {S}}\left( t \right) =-x^{2}-2xt-\left( b_{i}^{\mathrm {S}}-\mathrm {2}xB_{i} \right) . \end{aligned}$$

System (12) can now be written as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} x^{2}-\left( a_{i}-B_{i}-x \right) ^{2}+b_{i}^{\mathrm {S}}=b_{i}^{\mathrm {P}} \\ x^{2}-\left( a_{i}-A_{i}-x \right) ^{2}+2x\left( A_{i}-B_{i-1} \right) +b_{i-1}^{\mathrm {S}}=b_{i}^{\mathrm {P}} \\ \end{array}} \right. , \end{aligned}$$

and then as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \left( B_{i}+A_{i} \right) x-\frac{1}{4}\left( B_{i}-A_{i} \right) ^{2}+\left( b_{i}^{\mathrm {S}}-2xB_{i} \right) =b_{i}^{\mathrm {P}} \\ \left( B_{i}+A_{i} \right) x-\frac{1}{4}\left( B_{i}-A_{i} \right) ^{2}+\left( b_{i-1}^{\mathrm {S}}-2xB_{i-1} \right) =b_{i}^{\mathrm {P}} \\ \end{array}} \right. , \end{aligned}$$

Hence, $( b_{i}^{\mathrm {S}}-2xB_{i} )$ is independent of i, which we denote by a new constant c:

$$\begin{aligned} \left( b_{i}^{\mathrm {S}}-2xB_{i} \right) =c,\quad \hbox { for all } i. \end{aligned}$$

Consequently, system (12) simplifies to $b_{i}^{\mathrm {P}}=c^{\mathrm {P}}( A_{i},B_{i},c )$, where

$$\begin{aligned} c^{\mathrm {P}}\left( A,B,c \right) \equiv \left( B+A \right) x-\frac{1}{4}\left( B-A \right) ^{2}+c. \end{aligned}$$

The money-burning function for separated states (10) simplifies to $b^{\mathrm {S}}( t )=2xt+c$. Equilibrium utility $v^{{\Omega }}( t )$ can now be written as follows:

$$\begin{aligned} v^{{\Omega }} \left( t \right) = \left\{ {\begin{array}{ll} {- x^{2} - 2xt - c + \left( {B_{i} - t} \right) \left( {t - A_{i} } \right) } &{}\quad {{\text {if }}t \in \left( {A_{i} ,B_{i} } \right) } \\ { - x^{2} - 2xt - c} &{}\quad {{\text {if }}t \in \left( {B_{i} ,A_{{i + 1}} } \right) } \\ \end{array}} \right. \end{aligned}$$

Integrating $v^{{\Omega }}( t )$ over $t\in [ 0,\,1 ]$ yields the ex-ante expected utility of the Sender:

$$\begin{aligned} V^{\mathrm {S}}\left( {\Omega } \right) =-c-x^{2}-x+\frac{1}{6}\sum \limits _i \left( B_{i}-A_{i} \right) ^{3}. \end{aligned}$$

(17)

In (17), the summation extends on all pooling intervals, be they finite or infinite in numbers.

Step 2.

Let $P( {\Omega } )$ be an infinite partition. The set of marginal states $\{ A_{i} \}$ is infinite and has an accumulation point $\hat{A}$. It follows that for any $\varepsilon >0$, there are infinitely many marginal states either in a right neighborhood $( \hat{A},\hat{A}+\varepsilon )$ or a left neighborhood $( \hat{A}-\varepsilon ,\hat{A} )$ of $\hat{A}$. We consider the first possibility; the second case can be dealt with similarly.

Let us take an $\varepsilon \in ( 0,\,4x )$ and choose two marginal states $A_{n_{1}}$ and $A_{n_{2}}$ such that $A_{n_{1}}<A_{n_{2}}$ and $\{ A_{n_{1}},A_{n_{2}} \}\subset ( \hat{A},\hat{A}+\varepsilon )$. In $\Omega$, if the state is $t=A_{i}$, the Sender is indifferent between pooling with the states $t\in ( A_{i},B_{i} )$ or separating. In the latter case, she burns $b^{\mathrm {S}}( A_{i} )=2xA_{i}+c$. By continuity of the equilibrium utility function $v^{{\Omega }}( t )$, in state $\hat{A}$, the Sender gets the following equilibrium utility:

$$\begin{aligned} v^{{{\Omega }}} \big ( {\hat{A}} \big ) = \mathop {\lim }\limits _{{k \rightarrow \infty }} v^{{{\Omega }}} \left( {A_{{i_{k} }} } \right) = u\big ( {\hat{A} ,\hat{A},x} \big ) - b^{{\text {S}}} \big ( {\hat{A}} \big ) = - x^{2} - 2x\hat{A} - c, \end{aligned}$$

where the limit is taken over any decreasing subsequence of $\{ A_{i_{k}} \}$ that converges to $\hat{A}$. Accordingly, $V^{\mathrm {S}}( {\Omega } )$ can be written as follows.

$$\begin{aligned} V^{{\text {S}}} = - c - x^{2} - x + \frac{1}{6}\left( {\mathop {\sum }\limits _{{A_{i}< \hat{A}}} D_{i} ^{3} + \mathop {\sum }\limits _{{\hat{A} \le A_{i}< A_{{n_{1} }} }} D_{i} ^{3} + \mathop {\sum }\limits _{{A_{{n_{1} }} \le A_{i} < A_{{n_{2} }} }} D_{i} ^{3} + \mathop {\sum }\limits _{{A_{{n_{2} }} \le A_{i} }} D_{i} ^{3} } \right) . \end{aligned}$$

Let us now consider an equilibrium ${\Omega }_{\mathrm {1}}$ with a partition $P( {\Omega }_{\mathrm {1}} )$ in which all states $t\in ( \hat{A},A_{n_{2}} )$ are pooled, and in all other states, the Sender sends the same signal as she does in ${\Omega }$, i.e.,

$$\begin{aligned} P\left( {\Omega }_{\mathrm {1}} \right) =\big \{ \left( A_{i},B_{i} \right) \vert \, \left( A_{i},B_{i} \right) {\cap }\big ( \hat{A},A_{n_{\mathrm {2}}} \big )=\emptyset \big \}\,{\cup }\,\big \{ \big ( \hat{A},A_{n_{\mathrm {2}}} \big ) \big \}. \end{aligned}$$

In ${\Omega }_{\mathrm {1}}$, if the state is $t\in ( \hat{A},A_{n_{2}} )$, the Sender burns:

$$\begin{aligned} b_{1}^{\mathrm {P}}\left( t \right)= & {} c^{\mathrm {P}}\big ( \hat{A},A_{n_{2}},c \big )=\big ( A_{n_{2}}+\hat{A} \big )x-\frac{1}{4}\big ( A_{n_{2}}-\hat{A} \big )^{2}+c \\= & {} b^{\mathrm {S}}\big ( \hat{A} \big )+\big ( A_{n_{2}}-\hat{A} \big )\left( x-\frac{1}{4}\big ( A_{n_{2}}-\hat{A} \big ) \right)>b^{\mathrm {S}}\big ( \hat{A} \big ) \\&+\frac{1}{4}\big (A_{n_{2}}-\hat{A} \big )\big ( 4x-\varepsilon \big )>0. \end{aligned}$$

Thus, constructing ${\Omega }_{\mathrm {1}}$ is always feasible. In ${\Omega }_{\mathrm {1}}$, the sender gets utility $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )$:

$$\begin{aligned} V^{\mathrm {S}}\left( {\Omega }_{\mathrm {1}} \right) =-c-x^{2}-x+\frac{1}{6}\left( \sum \limits _{A_{i}<\hat{A}} D_{i}^{3} +\big ( A_{n_{2}}-\hat{A} \big )^{3}+\sum \limits _{A_{n_{2}}\le A_{i}} D_{i}^{3} \right) . \end{aligned}$$

Step 3.

Let us evaluate the difference $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )-V^{\mathrm {S}}( {\Omega } )$ is:

$$\begin{aligned} V^{\mathrm {S}}\left( {\Omega }_{\mathrm {1}} \right) -V^{\mathrm {S}}\left( {\Omega } \right)= & {} \frac{1}{6}\left( \big ( A_{n_{2}}-\hat{A} \big )^{3}-\sum \limits _{{\hat{A}\le A}_{i}<A_{n_{1}}} D_{i}^{3} -\sum \limits _{{A_{n_{1}}\le A}_{i}<A_{n_{2}}} D_{i}^{3} \right) \\\ge & {} \frac{1}{6}\left( \big ( A_{n_{2}}-\hat{A} \big )^{3}-\big ( A_{n_{1}}-\hat{A} \big )^{3}-\big ( A_{n_{2}}-A_{n_{1}} \big )^{3} \right) >0. \end{aligned}$$

Thus, ${\Omega }$ is suboptimal. $\square$

Proof of Lemma 3

We prove the lemma is 4 steps. In step 1, we show that it is never optimal to burn money in two neighboring intervals i and $( i+1 )$. In step 2, we show that neither is it optimal to burn money in two intervals even if there are some pooling intervals without money burning in between. Steps 1 and 2 together imply that the Sender burns money in at most one interval in ${\Omega }^{{*}}$. In step 3, we show that it is not optimal to burn money in the first interval, and in step 4, we show that neither is it optimal to burn money in an interval $j\ge 3$. The statement of the lemma then follows immediately.

Step 1.

We prove by contradiction. Suppose that in ${\Omega }^{{*}}$ money burning take place in two neighboring intervals i and $( i+1 )$, so that $c^{\mathrm {P}}( A_{i},A_{i+1},c )>$ and $c^{\mathrm {P}}( A_{i+1},A_{i+2},c )>0$. We consider a small change in $A_{i+1}$ for which the last two inequalities still hold, and consider utility $V^{\mathrm {S}}=V^{\mathrm {S}}( {\Omega } )$ as a function of $A_{i+1}$. The necessary conditions for a local maximum are $\frac{dV^{\mathrm {S}}}{dA_{i+1}}=0$ and $\frac{d^{2}V^{\mathrm {S}}}{dA_{i+1}^{2}}{\le 0}$. However, the objective function is convex in $A_{i+1}$, $\frac{d^{2}V^{\mathrm {S}}}{dA_{i+1}^{2}}=( A_{i+2}-A_{i} )>0$, contradicting the optimality of ${\Omega }^{{*}}$.

Step 2.

The proof is by contradiction. Suppose that in ${\Omega }^{{*}}$, money burning takes place in two intervals $( k-n-1 )$ and k, $k\ge 3$, i.e., there are $n\ge 1$ pooling intervals without money burning in between two intervals where money burning takes place. Thus, $b_{k}^{\mathrm {P}}>0$, $b_{k-n-1}^{\mathrm {P}}>0$, and $b_{i}^{\mathrm {P}}=0$ for all $i=( k-n ),\ldots ,( k-1 )$. We construct another equilibrium ${\Omega }_{\mathrm {1}}$ such that $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )>V^{\mathrm {S}}( {\Omega }^{{*}} )$, which contradicts the optimality of ${\Omega }^{{*}}$.

We consider a family of equilibria ${\Omega }$ which have the same value of c, the same marginal states below $A_{k-n}$ and above $A_{k}$, i.e., in the set $[ 0,A_{k-n-1} ]\cup [ A_{k+1},1 ]$, and no money burning in the set $( A_{k-n},A_{k} )$. It is easy to see that the choice of $A_{k}$ uniquely defines $A_{i}$ for $i=( k-n ),\ldots ,( k-1 )$ through $b_{i}^{\mathrm {P}}=c^{\mathrm {P}}( A_{i},A_{i+1},c )$ as follows:

$$\begin{aligned} A_{i}=A_{i+1}-2\left( \sqrt{x^{2}+2xA_{i+1}+c} -x \right) . \end{aligned}$$

By induction on i, it can be shown that this recursive equation implies:¹⁰

$$\begin{aligned} A_{k-j}=A_{k}-2j\left( s\left( A_{k},c \right) -jx \right) \quad \hbox { for } j=1,\ldots ,n, \end{aligned}$$

(18)

where we have defined

$$\begin{aligned} s\left( A,c \right) \equiv \sqrt{x^{2}+2xA+c}. \end{aligned}$$

The lengths of the intervals $D_{i}=( A_{i+1}-A_{i} )$ can be written as follows:

$$\begin{aligned} D_{k-j}=A_{k-j+1}-A_{k-j}=2\left( s\left( A_{k},c \right) -\left( 2j-1 \right) x \right) ,\quad \hbox { for } j=1,\ldots ,n. \end{aligned}$$

The constraints $c^{\mathrm {P}}( A_{i},A_{i+1},c )=0$ imply that for $j=1,\ldots ,n$:

$$\begin{aligned} D_{k-j}^{\mathrm {3}}=4x\big ( A_{k-j+1}^{\mathrm {2}}-A_{k-j}^{\mathrm {2}} \big )+4c\left( A_{k-j+1}-A_{k-j} \right) . \end{aligned}$$

(19)

In what follows, we consider $V^{\mathrm {S}}=V^{\mathrm {S}}( {\Omega } )$ as a function of $A_{k}$:

$$\begin{aligned} V^{\mathrm {S}}=-c-x^{2}-x+\frac{1}{6}\sum \limits _{i=1}^N D_{i}^{3}. \end{aligned}$$

In the rest of step 2, we show that $V^{\mathrm {S}}( {\Omega } )$ is convex in $A_{k}$ so that an interior maximum does not exist. The maximum necessarily violates one of the restrictions $D_{k-n-1}>$, $D_{k}>0$, $b_{k}^{\mathrm {P}}>0$, or $b_{k-n-1}^{\mathrm {P}}>0$. Consequently, in any open neighborhood of $A_{k}$, there exists an $\tilde{A}_{k}$ and the corresponding equilibrium ${\Omega }_{\mathrm {1}}$ so that $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )>V^{\mathrm {S}}( {\Omega }^{{*}} )$.

We compute the first-order derivative:

$$\begin{aligned} \frac{dV^{\mathrm {S}}}{dA_{k}}= & {} \frac{1}{6}\frac{d}{dA_{k}}\left( \sum \limits _{i=1}^{k-n-2} D_{i}^{3} +\sum \limits _{i=k+1}^N D_{i}^{3} \right) \\&+\frac{1}{6}\frac{d}{dA_{k}}\left( D_{k-n-1}^{3}+\sum \limits _{j=1}^n D_{k-j}^{3} +D_{k}^{3} \right) . \end{aligned}$$

Since $D_{i}$ is independent of $A_{k}$ for $i\le k-n-2$ or $i\ge k+1$, the first term vanishes:

$$\begin{aligned} \frac{dV^{\mathrm {S}}}{dA_{k}}= & {} \frac{1}{6}\frac{d}{dA_{k}}\left( D_{k-n-1}^{3}+\sum \nolimits _{j=1}^n D_{k-j}^{3} +D_{k}^{3} \right) \\= & {} \frac{1}{6}\frac{d}{dA_{k}}\left( D_{k-n-1}^{3}+4x\left( A_{k}^{2}-A_{k-n}^{2} \right) +4c\left( A_{k}-A_{k-n} \right) +D_{k}^{3} \right) \\= & {} \frac{1}{6}\left( \left( 3D_{k-n-1}^{2}-8xA_{k-n}-4c \right) \frac{dA_{k-n}}{dA_{k}}+8xA_{k}+4c-3D_{k}^{2} \right) . \end{aligned}$$

The second-order derivative is:

$$\begin{aligned} \frac{d^{2}V^{\mathrm {S}}}{dA_{k}^{\mathrm {2}}}= & {} \left( D_{k-n-1}\left( \frac{dA_{k-n}}{dA_{k}} \right) ^{2}+\frac{1}{2}D_{{k-n-1}} {}^{2}\frac{d^{2}A_{k-n}}{dA_{k}^{\mathrm {2}}}+D_{k} \right) \nonumber \\&+\frac{1}{6}\left( 8x\left( 1-\left( \frac{dA_{k-n}}{dA_{k}} \right) ^{2} \right) -4\left( 2xA_{k-n}+c \right) \frac{d^{2}A_{k-n}}{dA_{k}^{\mathrm {2}}} \right) \end{aligned}$$

(20)

Evaluating $\frac{dA_{k-n}}{dA_{k}}$ and $\frac{d^{2}A_{k-n}}{dA_{k}^{\mathrm {2}}}$ yields:

$$\begin{aligned} \frac{dA_{k-n}}{dA_{k}}= & {} 1-2n\frac{ds\left( A_{k},c \right) }{dA_{k}}=1-\frac{2xn}{s\left( A_{k},c \right) }\quad \hbox { and }\quad \\ \frac{d^{2}A_{k-n}}{dA_{k}^{\mathrm {2}}}= & {} \frac{2xn}{s^{2}\left( A_{k},c \right) }\cdot \frac{ds\left( A_{k},c \right) }{dA_{k}}=\frac{2x^{2}n}{s^{3}\left( A_{k},c \right) }>0. \end{aligned}$$

Hence, the first term in brackets in (20) is strictly positive, so that:

$$\begin{aligned} \frac{d^{2}V^{\mathrm {S}}}{dA_{k}^{\mathrm {2}}}> & {} \frac{1}{6}\left( 8x\left( 1-\left( \frac{dA_{k-n}}{dA_{k}} \right) ^{2} \right) -4\left( 2xA_{k-n}+c \right) \frac{d^{2}A_{k-n}}{dA_{k}^{\mathrm {2}}} \right) \\= & {} \frac{4x^{2}n\left( 4\left( s\left( A_{k},c \right) -xn \right) s\left( A_{k},c \right) -2xA_{k-n}-c \right) }{3s^{3}\left( A_{k},c \right) } \\= & {} \frac{4x^{2}n\left( 3s^{2}\left( A_{k},c \right) -\left( 4n^{2}-1 \right) x^{2} \right) }{3s^{3}\left( A_{k},c \right) }. \end{aligned}$$

Finally, $D_{k-n}$ implies $s( A_{k},c )>( 2n-1 )x$, which yields:

$$\begin{aligned} \frac{d^{2}V^{\mathrm {S}}}{dA_{k}^{\mathrm {2}}}>\frac{4x^{4}n}{3s^{3}\big ( A_{k},c \big )}\big ( 3\big ( 2n-1 \big )^{2}-\big ( 4n^{2}-1 \big ) \big )=\frac{16x^{4}n\left( n-1 \right) \left( 2n-1 \right) }{3s^{3}\big ( A_{k},c \big )}\ge 0. \end{aligned}$$

Hence, $V^{\mathrm {S}}$ is strictly convex in $A_{k}$.

Step 3.

Suppose that $N=1$ so that $P( {\Omega } )=\{ ( 0,1 ) \}$. Clearly, the Sender prefers an equilibrium with $b_{1}^{\mathrm {P}}=0$ over one with $b_{1}^{\mathrm {P}}>0$. Suppose, therefore, that $N\ge 2$, and $b_{1}^{\mathrm {P}}>0$ and $b_{i}^{\mathrm {P}}=0$ for all $i=2,\ldots ,N$. Using $b_{i}^{\mathrm {P}}=0$, we write c and $A_{i}$ as functions of $A_{N}$ through (18):

$$\begin{aligned}&c\left( A_{N} \right) =\frac{1}{4}\left( 1-A_{N} \right) ^{2}-\left( 1+A_{N} \right) x,\quad \hbox { and} \nonumber \\&A_{i}\left( A_{N} \right) =1-\left( N+1-i \right) \left( \left( 1-A_{N} \right) -2\left( N-i \right) x \right) \quad \hbox { for }i=2,\ldots ,N.\qquad \end{aligned}$$

(21)

In what follows, we consider $V^{\mathrm {S}}=V^{\mathrm {S}}( {\Omega } )$ as a function of $A_{N}$. Using (19) yields

$$\begin{aligned} V^{\mathrm {S}}=-c-x^{2}-x+\frac{1}{6}\big ( A_{2}^{3}+4x\big ( 1-A_{2}^{2} \big )+4c\big ( 1-A_{2} \big ) \big ), \end{aligned}$$

and its derivative

$$\begin{aligned}&\frac{dV^{\mathrm {S}}}{dA_{N}}\\&\quad =\frac{\left( N-1 \right) \left( {3A}_{2}^{2}-8xA_{2}-\left( 1-A_{N} \right) ^{2}+4x\left( 1+A_{N} \right) \right) -\left( 2\left( 1-A_{2} \right) -3 \right) \left( \left( 1-A_{N} \right) +2x \right) }{6}. \end{aligned}$$

In the rest of step 3, we show that $\frac{dV^{\mathrm {S}}}{dA_{N}}>0$ so that $V^{\mathrm {S}}$ is strictly increasin in $A_{N}$ and, therefore, ${\Omega }$ is not optimal. Using (21), we express $A_{N}$ it in terms of $A_{2}$:

$$\begin{aligned} A_{N}=\frac{A_{2}}{N-1}-2\left( N-2 \right) x+\frac{N-2}{N-1}. \end{aligned}$$

Then, we express $\frac{dV^{\mathrm {S}}}{dA_{N}}$ in terms of $A_{2}$:

$$\begin{aligned} \frac{dV^{\mathrm {S}}}{dA_{N}}\left( A_{2} \right) =\frac{N-1}{6}\left( \frac{3A_{2}\left( 1+A_{2}\left( N-2 \right) N \right) }{\left( N-1 \right) ^{2}}+2x\left( 3-\left( N-2 \right) 2Nx \right) \right) . \end{aligned}$$

Next, we define $\hat{A}$ implicitly by $c^{\mathrm {P}}( \hat{A},A_{2},c )=0$:

$$\begin{aligned} \hat{A}\equiv 1-N\left( \left( 1-A_{N} \right) -2\left( N-1 \right) x \right) =1-N\left( \frac{1-A_{2}}{N-1}-2x \right) . \end{aligned}$$

Since $\frac{\partial c^{\mathrm {P}}}{\partial A}=x+\frac{B-A}{2}>0$, and ${b_{1}^{\mathrm {P}}=c}^{\mathrm {P}}( 0,A_{2},c )>0$ by our assumption, it must be the case that $\hat{A}<0$, which is equivalent to $2Nx<\frac{N}{N-1}( 1-A_{2} )-1$. Hence,

$$\begin{aligned}&3-\left( N-2 \right) 2Nx>3-\left( N-2 \right) \left( \frac{N}{N-1}\left( 1-A_{2} \right) -1 \right) \\&\quad =\frac{\left( 2N-1 \right) +\left( N-2 \right) NA_{2}}{N-1}>0. \end{aligned}$$

and, therefore, $\frac{dV^{\mathrm {S}}}{dA_{N}}( A_{N} )>0$. This ends step 3.

Step 4.

The proof is by contradiction. Suppose that in ${\Omega }^{{*}}$, money burning only takes place in interval $( k+1 )$, $k\ge 2$, i.e., $b_{k+1}^{\mathrm {P}}>0$ and $b_{i}^{\mathrm {P}}=0$ for $i=1,\ldots ,k$. We construct another equilibrium ${\Omega }_{\mathrm {1}}$ such that $V^{\mathrm {S}}( {\Omega }_{\mathrm {1}} )>V^{\mathrm {S}}( {\Omega }^{{*}} )$, which contradicts the optimality of ${\Omega }^{{*}}$.

Conditions $b_{i-1}^{\mathrm {P}}=0$ for $i=2,\ldots ,k+1$ determine parameter c and all equilibrium marginal states $A_{i}$ as functions of $A_{2}$:

$$\begin{aligned} c\left( A_{2} \right) =\frac{1}{4}A_{2}^{2}-x\,A_{2},\quad \hbox { and }\quad A_{i}\left( A_{2} \right) =\left( i-1 \right) \left( 2x\left( i-2 \right) +A_{2} \right) . \end{aligned}$$

The contribution of intervals $( k+1 )$ and $( k+\mathrm {2} )$ into the objective $V^{\mathrm {S}}( {\Omega } )$ is $\frac{\mathrm {1}}{\mathrm {6}}( D_{k+1}^{3}+D_{k+2}^{3} )$.

Let us consider an equilibrium ${\Omega }_{\mathrm {1}}$ with the same marginal states as in ${\Omega }^{{*}}$ except for $A_{k+1}$. In ${\Omega }_{\mathrm {1}}$ we take $A_{k+1}=\tilde{A}_{k+1}$ where $\tilde{A}_{k+1}$ is implicitly defined by $c^{\mathrm {P}}( \tilde{A}_{k+1},A_{k+2},c )=0$. In other words, we take

$$\begin{aligned} \tilde{A}_{k+1}=A_{k+2}-2\left( \sqrt{x^{2}+2xA_{k+2}+c} -x\right) . \end{aligned}$$

In the rest of step 4, we show (a) that $\tilde{A}_{k+1}\in ( A_{k},A_{k+1} )$ and $c^{\mathrm {P}}( A_{k},\tilde{A}_{k+1},c )>0$ so that the construction of ${\Omega }_{\mathrm {1}}$ is feasible, and (b) that:

$$\begin{aligned} H{\equiv 6}\left( V^{\mathrm {S}}\left( {\Omega }_{\mathrm {1}} \right) -V^{\mathrm {S}}\left( {\Omega } \right) \right) >0, \end{aligned}$$

so that ${\Omega }^{{*}}$ is suboptimal.

• (a) We fix the value of $A_{k+1}$, use notation $v\equiv D_{k+2}=( A_{k+2}-A_{k+1} )>0$, and consider $A_{k+2}$ as a function of v, i.e., $A_{k+2}( v )=A_{k+1}+v$. Similarly, we consider functions

  $$\begin{aligned} \tilde{A}_{k+1}\left( v \right)= & {} A_{k+2}\left( v \right) -2\left( \sqrt{x^{\mathrm {2}}+2xA_{k+2}\left( v \right) +c} -x\right) ,\quad \hbox { and} \\ \tilde{D}_{k+1}\left( v \right)\equiv & {} A_{k+2}\left( v \right) -\tilde{A}_{k+1}\left( v \right) =2\left( \sqrt{x^{\mathrm {2}}+2xA_{k+2}\left( v \right) +c} -x\right) . \end{aligned}$$

  Let us consider the function $\tilde{A}_{k+1}( v )$. First, we define a number $\hat{v}$ implicitly by $c^{\mathrm {P}}( A_{k+1},A_{k+1}+\hat{v},c )=0$. Since $c^{\mathrm {P}}( A,B,c )$ is a second-degree concave polynomial in B and:

  $$\begin{aligned} c^{\mathrm {P}}\left( A_{k+1},A_{k+1},c \right) =2xA_{k+1}+c=4x^{\mathrm {2}}k\left( k-1 \right) +\left( \mathrm {2}k-1 \right) xA_{\mathrm {2}}+\frac{\mathrm {1}}{\mathrm {4}}A_{\mathrm {2}}^{2}>0, \end{aligned}$$

  it follows that $c^{\mathrm {P}}( A_{k+1},A_{k+1}+v,c )>0$ for all $v\in ( 0,\hat{v} )$ by construction. Second, $\tilde{A}_{k+1}( \mathrm {0} )=A_{k}$ due to $b_{k}^{\mathrm {P}}=0$, and $\tilde{A}_{k+1}( \hat{v} )=A_{k+1}$ by the definition of $\hat{v}$. Third, we show that $\tilde{A}_{k+1}( v )$ is monotonically increasing on $v\in ( 0,\hat{v} )$, which proves $\tilde{A}_{k+1}( v )\in ( A_{k},A_{k+1} )$. To this end, we compute the derivatives are:

  $$\begin{aligned} \frac{d\tilde{A}_{k+1}}{dv}= & {} 1-\frac{\mathrm {2}x}{\sqrt{x^{\mathrm {2}}+2xA_{k+2}+c} }=\frac{\tilde{D}_{k+1}-2x}{\tilde{D}_{k+1}+2x},\quad \hbox { and} \\ \frac{d\tilde{D}_{k+1}}{dv}= & {} 1-\frac{d\tilde{A}_{k+1}}{dv}=\frac{\mathrm {4}x}{\tilde{D}_{k+1}+2x}>0. \end{aligned}$$

  Since $\tilde{D}_{k+1}( \mathrm {0} )=4kx+A_{\mathrm {2}}>2x$, it follows that $\tilde{D}_{k+1}( v )>2x$ and $\frac{d\tilde{A}_{k+1}}{dv}>0$.

• (b) The contribution of intervals $( {A_{k} ,\tilde{A}_{k+1} } )$ and $( {\tilde{A}_{k+1} ,A_{k+2} } )$ into the objective $\tilde{V}^{\mathrm{S}}$ is $\frac{1}{6}( {( {\tilde{A}_{k+1} -A_{k} } )^{3}+( {A_{k+2} -\tilde{A}_{k+1} } )^{3}} )$. Hence, $H\equiv 6( {\tilde{V}^{\mathrm{S}}-V^{\mathrm{S}}} )$ can be written as:

  $$\begin{aligned} H= & {} \big ( {A_{k+1} -\tilde{A}_{k+1} } \big )\left( {A_{k+2} -A_{k} } \right) \\&\times \left( {\sqrt{\left( {\left( {2k-1} \right) x+\frac{1}{2}A_{2} } \right) ^{2}+2xD_{k+2} } -\left( {\left( {2k-1} \right) x+\frac{1}{2}A_{2} } \right) } \right) >0, \end{aligned}$$

Thus, ${\Omega }^{*}$ is suboptimal, which ends the proof of part (b), step 4, and the whole lemma. $\square$