Skip to main content
SpringerLink
Log in

An improved machine tool volumetric error compensation method based on linear and squareness error correction method

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

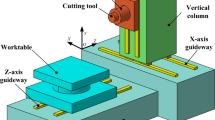
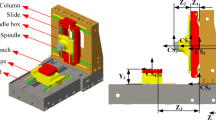
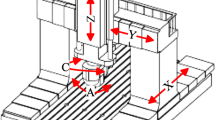
Abstract

Error compensation is one of effective and economical means to improve the machining accuracy of machine tools. The measurement accuracy of kinematic errors has great impact on the accuracy of machine tool error modeling. Some measurement errors are inevitably generated due to the distortion of the slide table and the limit of local measuring stroke. To solve these problems, an improved machine tool volumetric error compensation method is proposed in this paper, based on linear and squareness error correction method. The linear errors, including position errors and straightness errors, are corrected by considering the distance effect between optical mirror groups and the surface of worktable. The squareness errors are corrected through modifying local squareness errors measured with double ball bar to global squareness errors, with the aid of straightness errors measured with multi-laser calibrator. Then volumetric errors are obtained based on multi-body system theory, and volumetric diagonal errors are measured with laser interferometer. It is illustrated that the bidirectional systematic deviation of positioning of four volumetric diagonals reduced about 81.3%, 35.2%, 29.2%, and 4.5% respectively by using this improved machine tool volumetric error compensation method, and it is of obvious advantages in contrast with traditional compensation method with direct measurement data. The improved error compensation method proposed in this paper has universal applicability and has great significance on machine tool accuracy improvement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

LSECM:

Linear and squareness error correction method

DMM:

Direct measurement method

MLC:

Multi-laser calibrator

PSD:

Position sensitive detector

δx(X):

Positioning error of X axis

δy(Y):

Positioning error of Y axis

δz(Z):

Positioning error of Z axis

δy(X):

Straightness error of X axis in Y direction

δz(X):

Straightness error of X axis in Z direction

δx(Y):

Straightness error of Y axis in X direction

δz(Y):

Straightness error of Y axis in X direction

δx(Z):

Straightness error of Z axis in X direction

δy(Z):

Straightness error of Z axis in Y direction

εx(X):

Roll error of X axis

εy(X):

Pitch error of X axis

εz(X):

Yaw error of X axis

εy(Y):

Roll error of X axis

εx(Y):

Pitch error of Y axis

εz(Y):

Yaw error of Y axis

εz(Z):

Roll error of Z axis

εx(Z):

Pitch error of Z axis

εy(Z):

Yaw error of Z axis

α xy :

XY plane squareness error

β yz :

YZ plane squareness error

γ xz :

XZ plane squareness error

Δe x :

Volumetric error in X direction

Δe y :

Volumetric error in Y direction

Δe z :

Volumetric error in Z direction

\( {L}_{w-o}^{p_i} \) :

Distance from worktable to interference mirror in i-th error measurement

r m :

Length of squareness measuring rod

g β mn :

Pragmatic squareness error of MN plane

\( {{}^l\beta}_{mn}^{q,p} \) :

The measured squareness error of MN plane between measuring position q and p

References

  1. Lu Y, Islam M (2012) A new approach to thermally induced volumetric error compensation. Int J Adv Manuf Technol 62(9–12):1071–1085

    Article  Google Scholar 

  2. Du Z, Zhang S, Hong M (2010) Development of a multi-step measuring method for motion accuracy of NC machine tools based on cross grid encoder. Int J Mach Tool Manu 50(3):270–280

    Article  Google Scholar 

  3. Guo J, Li B, Liu Z, Hong J, Zhou Q (2016) A new solution to the measurement process planning for machine tool assembly based on Kalman filter. Precis Eng 43:356–369

    Article  Google Scholar 

  4. Yang J, Altintas Y (2013) Generalized kinematics of five-axis serial machines with non-singular tool path generation. Int J Mach Tool Manu 75(12):119–132

    Article  Google Scholar 

  5. Tian W, Gao W, Zhang D, Huang T (2014) A general approach for error modeling of machine tools. Int J Mach Tools Manuf 79:17–23

    Article  Google Scholar 

  6. Ekinci T, Mayer J (2007) Relationships between straightness and angular kinematic errors in machines. Int J Mach Tools Manuf 47(12–13):1997–2004

    Article  Google Scholar 

  7. Ekinci T, Mayer J, Cloutier G (2009) Investigation of accuracy of aerostatic guideways. Int J Mach Tools Manuf 49(6):478–487

    Article  Google Scholar 

  8. Majda P (2012) Modeling of geometric errors of linear guideway and their influence on joint kinematic error in machine tools. Precis Eng 36(3):369–378

    Article  Google Scholar 

  9. Zhang P, Chen Y, Zhang C, Zha J, Wang T (2018) Influence of geometric errors of guide rails and table on motion errors of hydrostatic guideways under quasi-static condition. Int J Mach Tools Manuf 125:55–67

    Article  Google Scholar 

  10. Weng L, Gao W, Lv Z, Zhang D, Liu T, Wang Y, Qi X, Tian Y (2018) Influence of external heat sources on volumetric thermal errors of precision machine tools. Int J Adv Manuf Technol 99(1–4):475–495

    Article  Google Scholar 

  11. Mekid S, Ogedengbe T (2010) A review of machine tool accuracy enhancement through error compensation in serial and parallel kinematic machines. Int J Precis Technol 1(3–4):251–286

    Article  Google Scholar 

  12. Wang K, Sheng X, Kang R (2010) Volumetric error modelling, measurement, and compensation for an integrated measurement-processing machine tool. Proc Inst Mech Eng C J Mech Eng Sci 224(11):2477–2486

    Article  Google Scholar 

  13. Li D, Feng P, Zhang J, Yu D, Wu Z (2014) An identification method for key geometric errors of machine tool based on matrix differential and experimental test. Proc Inst Mech Eng C J Mech Eng Sci 228(17):3141–3155

    Article  Google Scholar 

  14. Aguado S, Samper D, Santolaria J, Aguilar J (2012) Identification strategy of error parameter in volumetric error compensation of machine tool based on laser tracker measurements. Int J Mach Tool Manu 53(1):160–169

    Article  Google Scholar 

  15. Ezedine F, Linares JM, Sprauel JM, Chaves-Jacob J (2016) Smart sequential multilateration measurement strategy for volumetric error compensation of an extra-small machine tool. Precis Eng 43:178–186

    Article  Google Scholar 

  16. Linares JM, Chaves-Jacob J, Schwenke H, Longstaff A, Fletcher S, Flore J, Uhlmann E, Wintering J (2014) Impact of measurement procedure when error mapping and compensating a small CNC machine using a multilateration laser interferometer. Precis Eng 38(3):578–588

    Article  Google Scholar 

  17. Xiang S, Altintas Y (2016) Modeling and compensation of volumetric errors for five-axis machine tools. Int J Mach Tool Manu 101:65–78

    Article  Google Scholar 

  18. Givi M, Mayer J (2016) Optimized volumetric error compensation for five-axis machine tools considering relevance and compensability. CIRP J Manuf Sci Technol 12:44–55

    Article  Google Scholar 

  19. Zhou B, Wang S, Fang C, Sun S, Dai H (2017) Geometric error modeling and compensation for five-axis CNC gear profile grinding machine tools. Int J Adv Manuf Technol 92(5–8):2639–2652

    Article  Google Scholar 

  20. Fu G, Fu J, Gao H, Yao X (2017) Squareness error modeling for multi-axis machine tools via synthesizing the motion of the axes. Int J Adv Manuf Technol 89(9–12):2993–3008

    Article  Google Scholar 

  21. Khan AW, Chen W (2011) A methodology for systematic geometric error compensation in five-axis machine tools. Int J Adv Manuf Technol 53(5–8):615–628

    Article  Google Scholar 

  22. Vahebi M, Arezoo B (2018) Accuracy improvement of volumetric error modeling in CNC machine tools. Int J Adv Manuf Technol 95(5–8):1–15

    Google Scholar 

  23. Wu C, Fan J, Wang Q, Chen D (2018) Machining accuracy improvement of non-orthogonal five-axis machine tools by a new iterative compensation methodology based on the relative motion constraint equation. Int J Mach Tools Manuf 124:80–98

    Article  Google Scholar 

  24. Zha J, Xue F, Chen Y (2017) Straightness error modeling and compensation for gantry type open hydrostatic guideways in grinding machine. Int J Mach Tools Manuf 112:1–6

    Article  Google Scholar 

  25. Zhong X, Liu H, Mao X, Li B (2019) An optimal method for improving volumetric error compensation in machine tools based on squareness error identification. Int J Precis Eng Manuf:1–13

  26. Pezeshki M, Arezoo B (2017) Accuracy enhancement of kinematic error model of three-axis computer numerical control machine tools. Proc Inst Mech Eng B J Eng Manuf 231(11):2021–2030

    Article  Google Scholar 

  27. Pezeshki M, Arezoo B (2015) Kinematic errors identification of three-axis machine tools based on machined work pieces. Precis Eng S0141635915001798

  28. Peng W, Xia H, Wang S, Chen X (2017) Measurement and identification of geometric errors of translational axis based on sensitivity analysis for ultra-precision machine tools. Int J Adv Manuf Technol

  29. Wu C, Fan J, Wang Q, Pan R, Tang Y, Li Z (2018) Prediction and compensation of geometric error for translational axes in multi-axis machine tools. Int J Adv Manuf Technol 95(9–12):3413–3435

    Article  Google Scholar 

  30. Zhang Z, Liu Z, Cheng Q, Qi Y, Cai L (2017) An approach of comprehensive error modeling and accuracy allocation for the improvement of reliability and optimization of cost of a multi-axis NC machine tool. Int J Adv Manuf Technol 89(1–4):561–579

    Article  Google Scholar 

  31. ISO-230-6:2006, Test code for machine tools, part 6: determination of positioning accuracy on body and face diagonals (diagonal displacement tests)

  32. Rice JA (2006) Mathematical statistics and data analysis. Cengage Learning

Download references

Acknowledgments

We thank the reviewers’ comments.

Funding

The authors received the supports of the fund of National Nature Science Foundation of China No. 51775375, National Science and Technology Major Project of China under Grant No. 2018ZX04033001 and No. 2019ZX04005001, and the fund of Nature Science Foundation of Tianjin No. 17JCZDJC40300, No.18JCZDJC38700.

Author information

Authors and Affiliations

  1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University, Tianjin, 300354, China

    Weiguo Gao, Lingtao Weng, Guanwei Zhang, Yingjie Zheng & Jinhe Li

  2. College of Management and Economics, Tianjin University, Tianjin, 300072, China

    Jinyi Zhang

  3. School of Marine Science and Technology, Tianjin University, Tianjin, 300072, China

    Wenjie Tian

Authors
  1. Weiguo Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lingtao Weng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinyi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wenjie Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guanwei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Yingjie Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Jinhe Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Lingtao Weng or Wenjie Tian.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, W., Weng, L., Zhang, J. et al. An improved machine tool volumetric error compensation method based on linear and squareness error correction method. Int J Adv Manuf Technol 106, 4731–4744 (2020). https://doi.org/10.1007/s00170-020-04965-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-020-04965-z

Keywords

Search

Navigation