Spatial Cournot competition with non-extreme directional constraints

Abstract

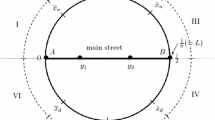
The circular city model and the linear city model are extended to allow for asymmetric directional transportation costs. A two-stage location-then-quantity model is proposed. We show that in the circular city model, maximal dispersion arises in equilibrium, while in the linear city model, the unique equilibrium is represented by both firms agglomerating in a non-central point of the segment.

Appendix

1.1 Equilibrium quantities and prices (circular city)

• Configuration 1

• $x\in [0,b]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=(p_x -tx)q_{A,x}$ and $\pi _B (x)=[p_x -r(b-x)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dot{q}_{A,1} ={[1+rb-x(r+2t)]}/3$ and $\dot{q}_{B,1} ={[1-2rb+x(2r+t)]}/3$. Therefore, the equilibrium price is: $\dot{p}_1 ={(1+br-rx+tx)}/3$.

• $x\in [b,x_A ]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=(p_x -tx)q_{A,x}$ and $\pi _B (x)=[p_x -t(x-b)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dot{q}_{A,2} ={[1-t(b+x)]}/3$ and $\dot{q}_{B,2} ={[1+t(2b-x)]}/3$. The equilibrium price is: $\dot{p}_2 ={[1-t(b-2x)]}/3$.

• $x\in [x_A ,x_B^1 ]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=[p_x -r(1-x)]q_{A,x}$ and $\pi _B (x)=[p_x -t(x-b)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dot{q}_{A,3} ={[1+t(x-b)-2r(1-x)]}/3$ and $\dot{q}_{B,3} ={[1+2t(b-x)+r(1-x)]}/3$. The equilibrium price is: $\dot{p}_3 ={(1+r-bt-rx+tx)}/3$.

• $x\in [x_B^1 ,1]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=[p_x -r(1-x)]q_{A,x}$ and $\pi _B (x)=[p_x -r(1+b-x)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dot{q}_{A,4} ={[1-r(1-b-x)]}/3$ and $\dot{q}_{B,4} ={[1-r(1+2b-x)]}/3$. Therefore, the equilibrium price is: $\dot{p}_4 ={[1+r(2+b-2x)]}/3$.

Therefore, the equilibrium profits of Firm $B$ are:

$$\begin{aligned}&\dot{\Pi }_B =\int \limits _0^b {\left[ {\dot{p}_1 -r(b-x)} \right] \dot{q}_{B,1} \mathrm{d}x}+\int \limits _b^{x_A } {\left[ {\dot{p}_2 -t(x-b)} \right] \dot{q}_{B,2} \mathrm{d}x} +\int \limits _{x_A }^{x_B^1 } {\left[ {\dot{p}_3 -t(x-b)} \right] \dot{q}_{B,3} \mathrm{d}x}\\&\quad \quad \quad \quad +\int \limits _{x_B^1 }^1 {\left[ {\dot{p}_4 -r(1+b-x)} \right] \dot{q}_{B,4} \mathrm{d}x} \\ \quad&=\frac{2(3-4b)b^{2}r^{3}t-2b^{3}r^{4}+3t^{2}-2b^{3}t^{4}+rt\left[ 6-3t+2(3-4b)b^{2}t^{2}\right] +r^{2}\left[ 3-3t+t^{2}(1+12b^{2}-12b^{3})\right] }{27(r+t)^{2}} \\ \end{aligned}$$

• Configuration 2

• $x\in [0,x_B^2 ]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=(p_x -tx)q_{A,x}$ and $\pi _B (x)=[p_x -t(1-b+x)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\ddot{q}_{A,1} ={[1+t(1-b-x)]}/3$ and $\ddot{q}_{B,1} ={[1-t(2-2b+x)]}/3$. Therefore, the equilibrium price is: $\ddot{p}_1 ={[1+t(1-b+2x)]}/3$.

• $x\in [x_B^2 ,b]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=(p_x -tx)q_{A,x}$ and $\pi _B (x)=[p_x -r(b-x)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\ddot{q}_{A,2} ={[1+r(b-x)-2tx]}/3$ and $\ddot{q}_{B,2} ={[1-2r(b-x)+tx]}/3$. Therefore, the equilibrium price is: $\ddot{p}_2 ={[1+tx+r(b-x)]}/3$.

• $x\in [b,x_A ]$: the same as Configuration 1. Therefore, $\dot{q}_{A,2} =\ddot{q}_{A,3}$, $\dot{q}_{B,2} =\ddot{q}_{B,3}$ and $\dot{p}_2 =\ddot{p}_3$.

• $x\in [x_A ,1]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=[p_x -r(1-x)]q_{A,x}$ and $\pi _B (x)=[p_x -t(x-b)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\ddot{q}_{A,4} ={[1-t(b-x)-2r(1-x)]}/3$ and $\ddot{q}_{B,4} ={[1+r(1-x)+2t(b-x)]}/3$. Therefore, the price in equilibrium is given by: $\ddot{p}_4 ={[1+r(1-x)-t(b-x)]}/3$.

Therefore, the equilibrium profits of Firm $B$ are:

$$\begin{aligned} {{\ddot{\Pi }}_B}&= \int _0^{x_B^2 } {\left[ { {{\ddot{p}}_1} -t(1-b+x)} \right] {{\ddot{q}}_{B,1}} \mathrm{d}x} \\&+\int \limits _{x_B^2 }^b {\left[ { {{\ddot{p}}_2} -r(b-x)} \right] {{\ddot{q}}_{B,2}} \mathrm{d}x}+\int _b^{x_A} {\left[ { {{\ddot{p}}_3} -t(x-b)} \right] {{\ddot{q}}_{B,3}} \mathrm{d}x} +\int \limits _{x_A }^1 {\left[ { {{\ddot{p}}_4} -t(x-b)} \right] {{\ddot{q}}_{B,4}} \mathrm{d}x} \\&= \frac{3t^{2}-t^{4}(2-6b+6b^{2})+r^{2}\left[ 3-3t+(1+6b-6b^{2})t^{2}\right] +rt\left[ 6-3t-2t^{2}(1-6b+6b^{2})\right] }{27(r+t)^{2}} \\ \end{aligned}$$

• Configuration 3

• $x\in [0,x_B^2 ]$: the same as Configuration 2. Therefore, $\ddot{q}_{A,1} =\dddot{q}_{A,1}$, $\ddot{q}_{B,1} =\dddot{q}_{B,1}$ and $\ddot{p}_1 =\dddot{p}_1$.

• $x\in [x_B^2 ,x_A ]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=(p_x -tx)q_{A,x}$ and $\pi _B (x)=[p_x -r(b-x)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dddot{q}_{A,2} ={[1+r(b-x)-2tx]}/3$ and $\dddot{q}_{B,2} ={[1-2r(b-x)+tx]}/3$. Therefore, the equilibrium price is: $\dddot{p}_2 ={[1+tx+r(b-x)]}/3$.

• $x\in [x_A ,b]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)=[p_x -r(1-x)]q_{A,x}$ and $\pi _B (x)=[p_x -r(b-x)]q_{B,x}$, respectively. Maximization of the profits functions yields the equilibrium quantities: $\dddot{q}_{A,3} ={[1-r(2-b-x)]}/3$ and $\dddot{q}_{B,3} ={[1+r(1-2b+x)]}/3$. Therefore, the equilibrium price is: $\dddot{p}_3 ={[1+r(1+b-2x)]}/3$.

• $x\in [b,1]$: Firm $A$’s and Firm $B$’s profits are: $\pi _A (x)\!=\![p_x \!-\!r(1-x)]q_{A,x}$ and $\pi _B (x)=[p_x -t(x-b)]q_{B,x}$, respectively. Maximization of the profits functions yields the following equilibrium quantities: $\dddot{q\!}_{A,4} =[1-t(b-x)-2r(1- x)]/3$ and $\dddot{q}_{B,4} ={[1+r(1-x)+2t(b-x)]}/3$. Therefore, the price in equilibrium is given by: $\dddot{p}_4 ={[1+r(1-x)-t(b-x)]}/3$.

Therefore, the equilibrium profits of Firm $B$ are:

$$\begin{aligned} \dddot{\Pi }_B&= \int _0^{x_B^2 } {\left[ {\dddot{p}_1 -t(1-b+x)} \right] \dddot{q}_{B,1} \mathrm{d}x} +\int _{x_B^2 }^{x_A } {\left[ {\dddot{p}_2 -r(b-x)} \right] \dddot{q}_{B,2} \mathrm{d}x} \\&+\int _{x_A }^b {\left[ {\dddot{p}_3 -r(b-x)} \right] \dddot{q}_{B,3} \mathrm{d}x}+\int _b^1 {\left[ {\dddot{p}_4 -t(x-b)} \right] \dddot{q}_{B,4} \mathrm{d}x} \\&= \frac{\left[ {\begin{array}{l} t^{2}[3-2t^{2}(1-b)^{3}]-2tr^{3}(1-4b)(1-b)^{2}-2r^{4}(1-b)^{3}\\ +tr\left[ 6-3t-2t^{2}(1-4b)(1-b)^{2}\right] +r^{2}\left[ 3-3t+t^{2}(1+12b-24b^{2}+12b^{3})\right] \\ \end{array}} \right] }{27(r+t)^{2}} \\ \end{aligned}$$

Proof of Proposition 1

First, we have $\dot{\Pi }_B (b=\frac{t}{r+t})=\ddot{\Pi }_B (b=\frac{t}{r+t})$ and $\ddot{\Pi }_B (b=\frac{r}{r+t})={\Pi }_B (b=\frac{r}{r+t})$. As a consequence, the profits function of Firm $B$ is continuous in $b$. Next, by differentiating $\dot{\Pi }_B$ and $\dddot{\Pi }_B$ with respect to $b$, we have: $\frac{\partial \dot{\Pi }_B }{\partial b}=\frac{2b[2rt-b(r+t)^{2}]}{9}\ge 0$, $\forall b\in [0,\frac{t}{r+t}]$, and $\frac{\partial {{\dddot{\Pi }}}_B }{\partial b}=-\frac{2(1-b)[2brt-(1-b)(r^{2}+t^{2})]}{9}\le 0$, $\forall b\in [\frac{r}{r+t},1]$. On the other hand, by differentiating $\ddot{\Pi }_B$ with respect to $b$, we get: $\frac{\partial \ddot{\Pi }_B }{\partial b}=\frac{2t^{2}(1-2b)}{9}$, and, $\frac{\partial ^{2}\ddot{\Pi }_B }{\partial b^{2}}=-\frac{4t^{2}}{9}<0$. Therefore, $\dot{\Pi }_B$ increases with $b$, ${\dddot{\Pi }}_B$ decreases with $b$, while $\ddot{\Pi }_B$ is maximized when $b=\frac{1}{2}$.¹⁰ It follows that the profits of Firm $B$ continuously increase when $b<\frac{1}{2}$, continuously decrease when $b>\frac{1}{2}$, and are maximized when $b=\frac{1}{2}$.$\square$

Proof of Proposition 2

Consider first the overall transportation costs under Configuration 1. They are:

$$\begin{aligned} \dot{T}&= \int _0^b {\left[ {tx\dot{q}_{A,1} +r(b-x)\dot{q}_{B,1} } \right] \mathrm{d}x} +\int _b^{x_A } {\left[ {tx\dot{q}_{A,2} +t(x-b)\dot{q}_{B,2} } \right] \mathrm{d}x} \\&+\int _{x_A }^{x_B^1 } {\left[ {r(1\!-\!x)\dot{q}_{A,3} \!+\!t(x-b)\dot{q}_{B,3} } \right] \mathrm{d}x} \!+\!\int _{x_B^1 }^1 {\left[ {r(1\!-\!x)\dot{q}_{A,4} \!+\!r(1+b-x)\dot{q}_{B,4} } \right] \mathrm{d}x} \\&= \frac{b^{3}(r+t)^{4}-3b^{2}rt(r+t)^{2}+rt[r(3-2t)+3t]}{9(r+t)^{2}} \end{aligned}$$

The overall transportation costs under Configuration 2 are given by:

$$\begin{aligned} \ddot{T}&= \int _0^{x_B^2 } {\left[ {tx{{\ddot{q}}_{A,1}} +t(1-b+x){{\ddot{q}}_{B,1}}} \right] \mathrm{d}x} +\int _{x_B^2 }^b {\left[ {tx{{\ddot{q}}_{A,2}} +r(b-x){{\ddot{q}}_{B,2}} } \right] \mathrm{d}x} \\&\quad +\int _b^{x_A } {\left[ {tx{{\ddot{q}}_{A,3}} +t(x-b){{\ddot{q}}_{B,3}} } \right] \mathrm{d}x} +\int _{x_A }^1 {\left[ {r(1-x) {{\ddot{q}}_{A,4}} +t(x-b){{\ddot{q}}_{B,4}} } \right] \mathrm{d}x} \\&= \frac{t\left[ t^{3}(1-3b+3b^{2})+rt(3+t-6bt+6b^{2}t)+r^{2}(3-t(2+3b-3b^{2}))\right] }{9(r+t)^{2}} \\ \end{aligned}$$

Finally, the overall transportation costs under Configuration 3 are given by:

$$\begin{aligned} \dddot{T}&= \int _0^{x_B^2 } {\left[ {tx\dddot{q}_{A,1} +t(1-b+x)\dddot{q}_{B,1} } \right] \mathrm{d}x} +\int _{x_B^2 }^{x_A } {\left[ {tx\dddot{q}_{A,2} +r(b-x)\dddot{q}_{B,2} } \right] \mathrm{d}x} \\&+\int _{x_A }^b {\left[ {r(1\!-\!x)\dddot{q}_{A,3} \!+\!r(b-x)\dddot{q}_{B,3} } \right] \mathrm{d}x} \!+\!\int _b^1 {\left[ {r(1\!-\!x)\dddot{q}_{A,4} \!+\!t(x-b)\dddot{q}_{B,4} } \right] \mathrm{d}x} \\&= \frac{\left[ {\begin{array}{l} r^{4}(1-b)^{3}+tr^{3}(1-4b)(1-b)^{2}+t^{4}(1-b)^{3}\\ +rt^{2}[3+t(1-4b)(1-b)^{2}]+tr^{2}\left[ 3-2t(1+3b-6b^{2}+3b^{3})\right] \\ \end{array}} \right] }{9(r+t)^{2}} \\ \end{aligned}$$

Next, note that $\dot{T}(b=\frac{t}{r+t})=\ddot{T}(b=\frac{t}{r+t})$ and $\ddot{T}(b=\frac{r}{r+t})={\dddot{T}}(b=\frac{r}{r+t})$. This implies that the transportation costs vary continuously with $b$. By differentiating $\dot{T}$ and ${\dddot{T}}$ with respect to $b$, we get: $\frac{\partial \dot{T}}{\partial b}=-\frac{b[2rt-b(r+t)^{2}]}{3}\le 0$, $\forall b\le \frac{t}{r+t}$, and $\frac{\partial {\dddot{T}}}{\partial b}=\frac{(1-b)[2brt-(1-b)(r^{2}+t^{2})]}{3}\ge 0$, $\forall b\in [\frac{r}{r+t},1]$. On the other hand, by differentiating $\ddot{T}$ with respect to $b$, we have: $\frac{\partial \ddot{T}}{\partial b}=-\frac{t^{2}(1-2b)}{3}$, and: $\frac{\partial ^{2}\ddot{T}}{\partial b^{2}}=\frac{2t^{2}}{3}\ge 0$. Therefore, $\dot{T}$ decreases with $b$, ${\dddot{T}}$ increases with $b$, while $\ddot{T}$ is minimized when $b=\frac{1}{2}$. As a consequence, the overall transportation costs continuously decrease when $b<\frac{1}{2}$, continuously increase when $b>\frac{1}{2}$, and are minimized when $b=\frac{1}{2}$.$\square$