Formation and behavior of counter-rotating vortex rings

Abstract

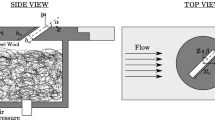
Concentric, counter-rotating vortex ring formation by transient jet ejection between concentric cylinders was studied numerically to determine the effects of cylinder gap ratio, $\frac{\Delta R}{R}$, and jet stroke length-to-gap ratio, $\frac{L}{\Delta R}$, on the evolution of the vorticity and the trajectories of the resulting axisymmetric vortex pair. The flow was simulated at a jet Reynolds number of 1000 (based on $\Delta R$ and the jet velocity), $\frac{L}{\Delta R}$ in the range 1–20, and $\frac{\Delta R}{R}$ in the range 0.05–0.25. Five characteristic flow evolution patterns were observed and classified based on $\frac{L}{\Delta R}$ and $\frac{\Delta R}{R}$. The results showed that the relative position, relative strength, and radii of the vortex rings during and soon after formation played a prominent role in the evolution of the trajectories of their vorticity centroids at the later time. The conditions on relative strength of the vortices necessary for them to travel together as a pair following formation were studied, and factors affecting differences in vortex circulation following formation were investigated. In addition to the characteristics of the primary vortices, the stopping vortices had a strong influence on the initial vortex configuration and effected the long-time flow evolution at low $\frac{L}{\Delta R}$ and small $\frac{\Delta R}{R}$. For long $\frac{L}{\Delta R}$ and small $\frac{\Delta R}{R}$, shedding of vorticity was sometimes observed and this shedding was related to the Kelvin–Benjamin variational principle of maximal energy for steadily translating vortex rings.