1 Introduction

Early optimal design of beams in order to maximize the first eigenfrequency were based on differential equation approaches, see Niordson (1965). Plates and other structural models then followed, see review by Grandhi (1993). The finite element (FE) approach of the present paper relates to a decided design domain, where the material densities of the elements are the design variables, and in addition the element constitutive components are subjected to design. This is termed free material optimization (FMO), often applied to static problems. In research related to semi-definite programming, eigenvalue constraints are also included, see Stingl et al. (2009).

The formulation and the theoretical results are valid for a large class of problems: 1D, 2D or 3D - numerical or analytical - continuum or structure. The limitations are set by a model described by symmetric, positive definite matrices for stiffness as well as for mass (for the system model including the assumed boundary conditions).

The present structural optimization may be divided into four steps, performed successively to obtain a redesign. First step is analysis of a current design, which is obtained by the standard procedure of subspace iteration. Second step is sensitivity analysis to obtain gradients of the eigenfrequencies with respect to element material density. A simple explicit formula for this is derived and presented. This is found to be important, due to its generality and presented by factors with direct physical interpretation. The third step is a redesign of material densities based on an optimality criterion, closely related to the gradients from sensitivity analysis. The numerical approach for solution is heuristic, earlier applied with good experience from other problem such as shape optimization for eigenfrequency control, see Pedersen and Pedersen (2005).

The fourth step immediately seems complicated, i.e., how to redesign each element constitutive matrix advantageously? A new optimality criterion for this step allows to redesign directly from the strain field corresponding to the current eigenmode. This is performed, automatically satisfying normalized, non-dimensional constitutive matrices with unit norms of trace and Frobenius. Mathematical proof of this is included. The fact that three strain components in 2D (6 in 3D) describe the anisotropy, means that not any constitutive matrix (6 components in 2D, 21 in 3D) can satisfy the optimality criterion, exemplified by that only zero Poisson’s ratio for isotropy is possible.

The layout of the paper is as follows. Analysis and sensitivity analysis are described in Section 2. In Section 3 the problem of material distribution to maximize the first eigenfrequency is stated with non-dimensional design parameters ρ e for the elements, size constraints 0<ρ min<ρ e <ρ max≤1 and a constraint on the amount of material \(V = {\sum }_{e} \rho _{e} V_{e}\), where V e is the volume of element e. In Section 4 the problem of design of constitutive matrices is presented in detail, i.e., the determination of the local anisotropy. Constraints that ensure symmetric, positive definite matrices are stated and furthermore these matrices are all normalized to unit norm of trace as well as of Frobenius norm. From a derived optimality criterion it is proved that these constraints are always satisfied. The case of semi-positive is numerically accounted for by always keeping a small amount of isotropy, just like material density should never vanish, say by ρ e ≥0.01.

In Section 5 two examples are chosen to verify the presented theory and applied procedure. With the actual design domains and boundary conditions, these examples may be seen as 2D versions of beam like models. The cantilever model illustrate how a fixed design domain at the free tip, force a more meaningful solution. In general robust convergence is found. The second example of a beam-bridge model is designed as a full model. This example illustrate mode switching between symmetric and antisymmetric modes. Even if only the first eigenfrequency is of interest, the subspace iteration is set to determine several eigenmodes, to get information on the frequency spectrum closest to given shift value (here zero).

2 Analysis and sensitivity analysis

For a given continuum/structure, analysis by subspace iteration, gives a series of eigenmodes, described individually by an eigenvector {D}, orthogonal to the other determined eigenvectors and normalized so that the specific kinetic energy T = 1. With this normalization of the eigenvector, the specific elastic energy U is numerically equal to the eigenvalue ω 2, i.e., for the numerical values U=ω 2=ω 2 T, where T and U are the time independent amplitudes.

Let us assume an eigenvalue problem described by the symmetric positive definite stiffness matrix [S] and the symmetric positive definite mass matrix [M]. An assumed simple (non-multiple) eigenvector is {D} from which the system specific elastic energy (twice the strain energy) is U and this energy may be accumulated from element energies U e . Analogously the system specific kinetic energy T may be accumulated from element specific kinetic energies T e .

In the sensitivity analysis we use the following results from subspace analysis

$$\begin{array}{@{}rcl@{}} \omega^{2}, U_{e}, T_{e} ~\text{with} ~\{D\}~ \text{normalized such that} \\ U = \sum U_{e} = \omega^{2}, T = \sum T_{e} = 1, \omega^{2} = U/T \end{array} $$
(1)

where U/T is the Rayleigh quotient. Further we define element Rayleigh quotients U e /T e , that in a somewhat loose notation are termed element squared frequencies

$$ {\omega^{2}_{e}} = \frac {U_{e}}{T_{e}} = \frac {\{D_{e}\}^{\text{T}} [S_{e}] \{D_{e}\}} {\{D_{e}\}^{\text{T}} [M_{e}] \{D_{e}\}} $$
(2)

As proved below in Section 2.1 the sensitivity of squared eigenfrequency ω 2 with respect to relative material density 0<ρ e ≤1 in element e is

$$ \frac {\partial \omega^{2}}{\partial \rho_{e}} = \frac {T_{e}}{T \rho_{e}} \left({\omega^{2}_{e}} - \omega^{2} \right) $$
(3)

This simple result with direct physical interpretation of each factor is valid for a general model described by positive definite, symmetric stiffness and mass matrices at the system level, for continuum as well as structure, analytical described as well numerical discretized. The gradient result (3) is for stiffness and mass linear depending on ρ e as proved in Section 2.1.

The element specific elastic energy U e , in linear displacements elements e follows directly from a displacement mode that give a constant elastic energy density u e and thus

$$ U_{e} = u_{e} \rho_{e} V_{e} $$
(4)

where V e is the geometric reference volume of the element e. Alternative evaluation of U e must be derived as the nominator in (2) for elements without constant energy density. The element specific kinetic energy T e in element e need to be determined from the element displacement mode {D e } and a consistent mass matrix with no coupling between x−,y−directions. The specific kinetic energy can then be divided into two terms, that exemplified for the x−direction is

$$ (T_{e})_{x} = \frac {m_{e}}{12} \{D_{e}\}_{x}^{\mathrm{T}} \left [\begin{array}{c c c} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array} \right ] \{D_{e}\}_{x} \quad \text {with} \quad m_{e} = \rho_{\text{M}} \rho_{e} V_{e} $$
(5)

where m e is the mass of element e. The mass density with physical dimension kg/m 3 is termed ρ M to distinguish from the non-dimensional material volume densities, that traditionally has the notation ρ e . From (5) a rather simple analytical expression follows. In general for a linear displacement FE model, the numerical calculations may be based on explicit formulas without numerical integration.

2.1 Derivation of eigenfrequency gradients

For linear stiffness interpolation, the expression (3) is derived in the following. For extension to non-linear interpolation functions see Pedersen and Pedersen (2012). The design parameters ρ e are assumed to be local, positive non-dimensional quantities in the interval 0<ρ e ≤1. We here assume both the element stiffness matrix [S e ] and the element mass matrix [M e ] to be proportional to ρ e , i.e.,

$$ [S_{e}] = \rho_{e} [\mathcal S_{e}], \quad [M_{e}] = \rho_{e} [\mathcal M_{e}] $$
(6)

with both \([\mathcal S_{e}]\) and \([\mathcal M_{e}]\) independent of design.

The gradient ∂ ω 2/∂ ρ e = ∂(U/T)/∂ ρ e is determined at the element level. To avoid extended indexing a hat notation is introduced by

$$ \widehat {\frac {\partial ()}{\partial \rho_{e}}} = \left( \frac {\partial ()}{\partial \rho_{e}} \right)_{\text{fixed ~ displacement}} = \left( \frac {\partial ()}{\partial \rho_{e}} \right)_{\text{fixed ~ strains}} \label {eq:hatdef} $$
(7)

and with this short notation the gradient is determined, finally at the element level

$$\begin{array}{@{}rcl@{}} \frac {\partial \omega^{2}}{\partial \rho_{e}} &=& \frac {\partial \omega^{2}}{\partial \{D\}} \frac {\partial \{D\}}{\partial \rho_{e}} + \widehat {\frac {\partial \omega^{2}}{\partial \rho_{e}}} = \frac {1}{T^{2}} \left( \widehat {\frac {\partial U}{\partial \rho_{e}}} T - \widehat {\frac {\partial T}{\partial \rho_{e}}} U \right) \\ &=& \frac {1}{T} \left( \widehat {\frac {\partial U_{e}}{\partial \rho_{e}}} - \omega^{2} \widehat {\frac {\partial T_{e}}{\partial \rho_{e}}} \right) \label {eq:gradient1} \end{array} $$
(8)

because ∂ ω 2/∂{D} = ∂(U/T)/∂{D}={0}T. This result, based on the assumption of symmetric matrices [S] and [M], is presented in Wittrick (1962) with further reference to Jacobi (1846). Inserting the assumptions of linear dependency \(\widehat {\partial U_{e} /\partial \rho _{e}}\) = U e /ρ e and \(\widehat {\partial T_{e} /\partial \rho _{e}}\) = T e /ρ e gives the local result where the gradient is expressed by local energies

$$ \frac {\partial \omega^{2}}{\partial \rho_{e}} = \frac {1}{T \rho_{e}} \left(U_{e} - \omega^{2} T_{e} \right) = \frac{T_{e}}{T \rho_{e}}\left({\omega^{2}_{e}} - \omega^{2}\right) $$
(9)

The gradient is proportional to the difference between the local ratio of energies (local Rayleigh quotient or termed local squared frequency) \({\omega ^{2}_{e}}\) and the system squared eigenfrequency ω 2.

From expression (9) follows directly the sign of the gradient as all T e ,T,ρ e are non-negative quantities

$$\begin{array}{@{}rcl@{}} \frac {\partial \omega^{2}}{\partial \rho_{e}} &>& 0 \quad \text {for} \quad {\omega_{e}^{2}} > \omega^{2}, \quad \frac {\partial \omega^{2}}{\partial \rho_{e}} < 0 \quad \text {for} \quad {\omega_{e}^{2}} < \omega^{2}, \\ \frac {\partial \omega^{2}}{\partial \rho_{e}} &=& 0 \quad \text {for} \quad {\omega_{e}^{2}} = \omega^{2} \end{array} $$
(10)

To increase the frequency of the continuum/structure we increase ρ e for \({\omega ^{2}_{e}} > \omega ^{2}\) and decrease ρ e for \({\omega _{e}^{2}} < \omega ^{2}\). A design change may be limited by the active constraint for material as stated in (11) and by the fact that sensitivity analysis will change when changing the design. The solution to these problems is obtained by the heuristic iterative optimization procedure, shortly described in Section 3.

3 A density optimization problem and its optimality criterion

We study the optimization problem to maximize an eigenvalue (assumed single and being the first one) ω 2 for a given amount of material, specified by the volume V. We assume this volume constraint to be active and state the problem with non-dimensional densities ρ e as design variables

$$\begin{array}{@{}rcl@{}} &&\!\!\!\!\!\text{Maximize} ~~ \omega^{2} \hspace*{6mm} \text{(objective)} \\ &&\!\!\!\!\!\text{for all densities} ~~ 0 < \rho_{\text{min}} \le \rho_{e} \le \rho_{\text{max}} \le 1 \hspace*{5.5mm} \text{(size limits)} \\ &&\!\!\!\!\!\text{and} ~~ g = \sum \rho_{e} V_{e} - V = 0 \hspace*{6mm} \text{(active constraint)} \end{array} $$
(11)

The optimality criterion for material distribution OC m with only a single, active constraint is proportionality between the gradients of the objective and the gradients of the constraint, i.e.,

$$ \frac {\partial \omega^{2}}{\partial \rho_{e}} = \lambda \frac {\partial g}{\partial \rho_{e}} = \lambda V_{e} ~~ \Rightarrow ~~ \lambda_{e} = \frac {1}{V_{e}} \frac {\partial \omega^{2}}{\partial \rho_{e}} = \lambda $$
(12)

with the same value λ e =λ for all elements (sub-domains) e having an active design parameter ρ e where ρ min<ρ e <ρ max. For a given design a number of different values λ e result, and we want to change the design in order for these values to become more equal for the active design elements (resulting in the unknown Lagrange multiplier λ). With linear stiffness interpolation the gradient ∂ ω 2/∂ ρ e is given in (9) and the optimality criterion for distribution of material density OC m is

$$ \lambda_{e} = \frac {T_{e}}{T} \frac {1}{\rho_{e} V_{e}} ({\omega^{2}_{e}} - \omega^{2}) = \lambda \label {eq:crit2} $$
(13)

3.1 Possible heuristic numerical procedure

The optimization problem (11) is by the OC m (12) converted to a problem of finding a continuum of best possible uniformity of the values of the local OC m (λ e ). Size limits and the active material volume constraint in (11) normally do not allow for satisfying the OC m everywhere. Iteratively the active size constraints are fulfilled.

A heuristic recursive procedure for optimization based on (13) is separated according to the sign of the gradients (sign of (\({\omega ^{2}_{e}} - \omega ^{2}\))). The redesign of the ρ e follows

$$\begin{array}{@{}rcl@{}} \text {For positive gradients} ~~ ({\omega^{2}_{e}} - \omega^{2} > 0) \\ (\rho_{e})_{\text{new}} =(\rho_{e})_{\text{current}} (1 + 4.0 \lambda_{e}/\lambda_{\text{max}})^{q} \eta \\ \text {For negative gradients} ~~ ({\omega^{2}_{e}} - \omega^{2} < 0) \\ (\rho_{e})_{\text{new}} =(\rho_{e})_{\text{current}} (1 - 0.8 \lambda_{e}/\lambda_{\text{min}})^{q} \eta \label {eq:rec1} \end{array} $$
(14)

where the values of λ min<0,λ max>0 are determined during the evaluation of the gradients. The specific values for control parameters in (14), 4.0,0.8,q=0.8, are chosen from experience, acting as a kind of move-limits and influence the number of recursive redesigns (number of eigenvalue analysis). The iteratively (without FE analysis) determined volume correction factor η relate to the fact that the densities at the limits ρ min or ρ max are not known in advance. Factor η strictly keep the specified volume by inner iteration where the ρ e at the size limits are localized. This is described in detail in Pedersen and Pedersen (2012). The value q=0.8 of the power also limits the change of ρ e in one redesign, and such a power (also with a lower value) is often applied for similar recursive procedures. The procedure is applied in the following examples, and have earlier been applied with success to different other problems.

4 Redesign of components for normalized constitutive matrices

The separation of the local constitutive matrix [L e ] is

$$\begin{array}{@{}rcl@{}} [L_{e}] &=& \rho_{e} E_{0} [\widetilde L_{e}] \\ &=& \rho_{e} E_{0} \left[ \begin{array}{c c c} (\widetilde L_{1 1 1 1})_{e} & (\widetilde L_{1 1 2 2})_{e} & \sqrt 2 (\widetilde L_{1 1 1 2})_{e} \\ (\widetilde L_{1 1 2 2})_{e} & (\widetilde L_{2 2 2 2})_{e} & \sqrt 2 (\widetilde L_{2 2 1 2})_{e} \\ \sqrt 2 (\widetilde L_{1 1 1 2})_{e} & \sqrt 2 (\widetilde L_{2 2 1 2})_{e} & 2 (\widetilde L_{1 2 1 2})_{e} \end{array} \right]\\ \end{array} $$
(15)

where \([\widetilde L_{e}]\) is a non-dimensional matrix of unit norm, i.e., a non-dimensional description of the material anisotropy. The discussion of this matrix is here of primary interest as the optimal determination of ρ e is described in Section 3. The dimensional modulus E 0 is a fixed constant.The problem of optimizing the first eigenfrequency by redesign of the anisotropy of element e is stated

$$\begin{array}{@{}rcl@{}} &&\!\!\text{Maximize} ~~ \omega^{2} \hspace {4mm} \text{(objective)} \\ &&\!\!\text{by redesign of non-dimensional constitutive components} \\ &&\!\!\widetilde L_{i j k l}~~ \text{(design parameters subject to unity Frobenius norm)} \\ &&\!\!\mathrm{h}\ = (\text{Frobenius}([\widetilde L])^{2} - 1 = 0 \hspace*{4mm} \text{(active constraints)}\\ \label {eq:OP2} \end{array} $$
(16)

The optimality criterion corresponding to this problem is termed OC a. With only a single, active constraint the criterion is again proportionality between the gradients of the objective and the gradients of the constraint, i.e.,

$$ \frac {\partial \omega^{2}}{\partial (\widetilde L_{i j k l})_{e}} = \varLambda \frac {\partial h}{\partial (\widetilde L_{i j k l})_{e}} $$
(17)

for which the involved gradients are then derived.

4.1 Gradients and resulting optimality criterion

The local gradient of the Rayleigh quotient with respect to the components of the local constitutive matrix is more simple than (9), because the mass distribution is unchanged (T an T e unchanged), here with hat notation as an alternative to extended index

$$\begin{array}{@{}rcl@{}} \frac {\partial \omega^{2}}{\partial (\widetilde L_{i j k l})_{e}} &=& \frac {\partial (U/T)}{\partial (\widetilde L_{ijkl})_{e}} = \frac {\widehat{\partial (U/T)}}{\partial (\widetilde L_{ijkl})_{e}} = \frac {\widehat{\partial (U_{e}/T_{e})}}{\partial (\widetilde L_{ijkl})_{e}} \\ &=& \frac {1}{T_{e}} \frac {\widehat{\partial U_{e}}}{\partial (\widetilde L_{ijkl})_{e}} = \frac {\rho_{e} V_{e}}{T_{e}} \frac {\widehat {\partial u_{e}}}{\partial (\widetilde L_{ijkl})_{e}} \\ &&\text {with fixed strains in} ~~ u_{e} = \{\epsilon\}_{e}^{\text{T}} [\widetilde L]_{e} \{\epsilon\}_{e} \end{array} $$
(18)

From the final relation in (18) then follows

$$\begin{array}{@{}rcl@{}}\frac {\partial \omega^{2}}{\partial (\widetilde L_{1 1 1 1})_{e}} &=& \frac {\rho_{e} V_{e}}{T_{e}} (\epsilon_{1 1} \epsilon_{1 1})_{e}, ~ \frac {\partial \omega^{2}}{\partial (\widetilde L_{2 2 2 2})_{e}} = \frac {\rho_{e} V_{e}}{T_{e}} (\epsilon_{2 2} \epsilon_{2 2})_{e}, \nonumber \\ \frac {\partial \omega^{2}}{\partial (\widetilde L_{1 2 1 2})_{e}} &=& 4 \frac {\rho_{e} V_{e}}{T_{e}}(\epsilon_{1 2} \epsilon_{1 2})_{e}, ~ \frac {\partial \omega^{2}}{\partial (\widetilde L_{1 1 2 2})_{e}} = 2 \frac {\rho_{e} V_{e}}{T_{e}} (\epsilon_{1 1} \epsilon_{2 2})_{e}, \nonumber \\ \frac {\partial \omega^{2}}{\partial (\widetilde L_{1 1 1 2})_{e}} &=& 4 \frac {\rho_{e} V_{e}}{T_{e}} (\epsilon_{1 1} \epsilon_{1 2})_{e}, ~ \frac {\partial \omega^{2}}{\partial (\widetilde L_{2 2 1 2})_{e}} = 4 \frac {\rho_{e} V_{e}}{T_{e}} (\epsilon_{2 2} \epsilon_{1 2})_{e}\end{array} $$
(19)

The gradients of the constraint h=F 2−1=0 are directly

$$\begin{array}{@{}rcl@{}} \frac {\partial h}{\partial (\widetilde L_{1 1 1 1})_{e}} &=& 2 (\widetilde L_{1 1 1 1})_{e}, ~~~ \frac {\partial h}{\partial (\widetilde L_{2 2 2 2})_{e}} = 2 (\widetilde L_{2 2 2 2})_{e}, \\ \frac {\partial h}{\partial (\widetilde L_{1 2 1 2})_{e}} &=& 8 (\widetilde L_{1 2 1 2})_{e}, ~~~ \frac {\partial h}{\partial (\widetilde L_{1 1 2 2})_{e}} = 4 (\widetilde L_{1 1 2 2})_{e}, \\ \frac {\partial h}{\partial (\widetilde L_{1 1 1 2})_{e}} &=& 8 (\widetilde L_{1 1 1 2})_{e}, ~~~ \frac {\partial h}{\partial (\widetilde L_{2 2 1 2})_{e}} = 8 (\widetilde L_{2 2 1 2})_{e} \end{array} $$
(20)

Comparing (19) and (20) it is seen that the optimality criterion OC a for 2D plane problems is satisfied for

$$ \left(\widetilde L_{i j k l}\right)_{e} = \left(\epsilon_{i j} \epsilon_{k l} / \left(\epsilon_{11}^{2} + \epsilon_{22}^{2} + 2 \epsilon_{12}^{2}\right) \right)_{e} $$
(21)

4.2 Proof of unit norms

As seen from (21) \([\widetilde L_{e}] = \{\alpha \}\{\alpha \}^{\text {T}}\) is described by such a dyadic product. Then by definitions of trace and Frobenius norms follows, that the values of trace and Frobenius norms are always equal and \([\widetilde L_{e}]\) is semi-positive definite.

$$\begin{array}{@{}rcl@{}} &&\text{Trace} [\widetilde L_{e}] = \text{Frobenius} [\widetilde L_{e}] = \{\alpha\}^{\text{T}}\{\alpha\} \\ &&\text {where} ~~ \{\alpha\}^{\text{T}}\{\alpha\} > 0 ~~ \text {for} ~~ \{\alpha\} \ne \{0\} \label {eq:norms} \end{array} $$
(22)

Omitting the index e for element, point or domain we proceed the discussion of the obtained constitutive matrix as described directly by the corresponding strain state. Although a constitutive matrix is not necessary obtainable as a dyadic product, this will be the case for the optimal constitutive matrix, where the important result in 2D plane problems with normalization to unit norms is

$$\begin{array}{@{}rcl@{}} &&[\widetilde L] = \{\alpha\}\{\alpha\}^{\text{T}} ~~ \text {with} \\ &&\{\alpha\}^{\text{T}} = \{ \epsilon_{11} ~~ \epsilon_{22} ~~ \sqrt 2 \epsilon_{12} \} / \sqrt {\epsilon_{11}^{2} + \epsilon_{22}^{2} + 2 \epsilon_{12}^{2}} \label {eq:dyad2D} \end{array} $$
(23)

That the optimal constitutive matrix of unit norms in 2D is described by only three parameters (the strain components) limits the possibilities for a matrix with normally up to 6 independent parameters. An example is that an isotropic \([\widetilde L]\) is only possible with zero Poisson’s ratio and for this case \(\{\alpha \}^{\text {T}} = \{ 1 ~ 1 ~ 1 \} /\sqrt 3\).

Numerically the rate of change of the constitutive matrices are in each redesign limited by a non-dimensional step parameter 0≤β≤1 similar to the design approach for strength optimization in Pedersen and Pedersen (2013) where β=0.5 and β=0.1 were used, i.e.,

$$ [\widetilde L]_{\text {new}} = \beta [\widetilde L]_{\text{from (23)}} + (1 - \beta) [\widetilde L]_{\text {old}} $$
(24)

The design approach is initiated with \([\widetilde L]_{0} = [I]/3\), i.e., zero Poisson’s ratio isotropic material, non-dimensional and normalized. It is concluded that for a given strain state the optimized non-dimensional constitutive constitutive matrix is known with unit trace and Frobenius norm. Note, that with initial positive definite \([\widetilde L]\) it will for β<1 stay positive definite through the redesign iterations. For the present eigenfrequency problems, the numerical value β=0.2 is applied, and even with this rather low value fast convergence is obtained.

5 Two design examples

Two examples, each with four different amounts of material, are presented. First a cantilever problem where a fixed design domain is included so that a degenerated optimized design is avoided. The influence of the amount of material is illustrated and the redesign history is shown with and without redesign of anisotropy. The increase in the value of the first eigenfrequency with a factor up to 2.2 by only redesign of material distribution, while with including optimized constitutive matrices then with a factor up to 3.5.

The second example is a a simply supported beam-bridge with no fixed design domain. To some extent modeling with assumed symmetric eigenmode is possible for half the model, but the possibility of mode switching from symmetric mode to antisymmetric mode for extended redesign is illustrate. Figures show the history of resulting eigenfrequencies for four different problems with amount of material set to 20 %, 40 %, 60 % and 80 % of full amount of material, all with uniform initial designs and this means that the four initial problems have identical eigenfrequencies (in the figures normalized to unity).

5.1 Cantilever with fixed tip design

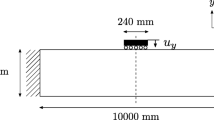
Figure 1 shows the dimensions and data applied for this example, and the 0.4m close to the tip is fixed to the initial value of the density. The mass and stiffness for this domain is thus different for the treated cases of 20 %, 40 %, 60 % and 80 % material, but without influence on the response of the initial uniform designs. The specific FE model has 16384 elements (128×32×4) and 16706 dof.

Fig. 1
figure 1

Data for the cantilever problem with fixed design near the free tip (0.4 m)

Full size image

With focus on the case of 20 % material Fig. 2 shows the history of results for two different redesign iterations. The dotted curve corresponds to redesigns of both density and anisotropy already from the first redesign, and convergence in 10 redesigns is observed. The full curve also give information about the result after 10 iterations where anisotropy in not optimized, and thus corresponds to a more traditional optimization. In this manner the essential importance of anisotropy is shown.

Fig. 2
figure 2

Iteration histories for the cantilever problem with 20 % material. Full line: only anisotropy redesign from redesign number 10. Broken line: anisotropy redesign from redesign number 0

Full size image

The initial design, illustrated in Fig. 3a is uniform material density (here ρ e all equal to 0.2). At the tip domain this is not changed. Figure 3b shows the distribution of values of optimality criterion for material distribution OC m for the initial design in Fig. 3a. The positive as well as negative values illustrate that a better material distribution can be obtained by redesign.

Fig. 3
figure 3

Designs and responses for the cantilever problem with 20 % of full material (a) Initial uniform isotropic design with (b) corresponding distribution of OC m values — (c) redesign after 10 isotropic density redesign with (d) corresponding distribution of OC m values — (e) redesign after further 10 density redesign including anisotropy redesign with (f) corresponding distribution of OC m values — (g) level of anisotropy resulting with (h) showing directions of maximum stiffness

Full size image

After 10 redesigns of only material density, the first eigenfrequency is increased with a factor close to 2.2, and Fig. 3c shows the optimized material distribution, when isotropy is kept. Figure 3d shows the distribution of OC m values for the optimized design in Fig. 3c. Note, that these OC m values are almost constant in domains corresponding to active design parameters ρ min<ρ e <ρ max. The white domains correspond to ρ e =ρ min=0.01, to be interpreted as holes.

After 10 more redesigns where the normalized constitutive matrices are also redesigned according to the simple formula (23) with modification (24) and the first eigenfrequency is increased further, now with a factor of 3.5. Figure 3e shows the optimized material distribution, being rather close to the distribution in Fig. 3c, meaning that the local constitutive redesign has only little influence on the optimized material distribution for this problem. Figure 3f shows the distribution of OC m values for the optimized design in Fig. 3e. Also these OC m values are almost constant in domains corresponding to active design parameters ρ min<ρ e <ρ max and the white domains correspond to ρ e =ρ min=0.01.

To illustrate the obtained anisotropy (in reality 6 components locally) Fig. 3g shows a value for the level of anisotropy, being a number between 1/3 for isotropy and 1 for single directional ”fiber”, as explained in the appendix. The largest normalized stiffness is used to illustrate the level of anisotropy. Figure 3h shows lines of direction for the use of this largest normalized stiffness. Although not complete it is found that the combination of Fig. 3e, g and h give a rather good illustration of the final optimized design.

The shown histories in Fig. 4 gives an impression of stable convergence for the chosen numerical procedure (14), with the same numerical control parameters 4.0,0.8,q=0.8 in (14) and β=0.2 in (24) for all cases. For the 80 % problem, the lower curve in Fig. 4 for the third redesign is decreasing, meaning that the design changes has been too large. With the kept numerical control parameters it illustrates that the procedure (14 – 24) is able to repair a too large design change. Note, that the fixed tip amount of material is depending upon the total amount of material. The initial uniform designs imply the equal eigenfrequencies for all four cases.

Fig. 4
figure 4

Iteration histories for the cantilever problem with 20 %, 40 %, 60 % and 80 % material

Full size image

5.2 Beam-bridge with mode switching

Figure 5 shows the dimensions and data applied for this example. The mass and stiffness for this domain is thus different for the treated cases of 20 %, 40 %, 60 % and 80 % of full material, but without influence on the response of the initial uniform designs. The specific FE model has 28416 elements (222×32×4) and 16706 dof.

Fig. 5
figure 5

Data for the beam-bridge problem with mode switching. Only midpoint supported in beam length direction

Full size image

Figure 6 shows the history of not only the first eigenfrequency but also the two closest eigenfrequencies obtained by subspace iteration. Almost multiple solutions are obtained and including mode switching. For the initial design the first eigenmode is a bending mode as shown in Fig. 7 which is also the case after only material density optimized, for the final optimized design the eigenmode is a longitudinal mode. This mode switching is due to the constitutive anisotropy design.

Fig. 6
figure 6

Iteration histories for the beam-bridge problem with 20 % material. Only anisotropy redesign from redesign number 10

Full size image
Fig. 7
figure 7

Designs and responses for the cantilever problem with 20 % of full material (a) Initial uniform isotropic design with (b) corresponding distribution of OC m values — (c) redesign after 10 isotropic density redesign with (d) corresponding distribution of OC m values — (e) redesign after further 10 density redesign including anisotropy redesign with (f) corresponding distribution of OC m values — (g) level of anisotropy resulting with (h) showing directions of maximum stiffness

Full size image

Note to Fig. 6: Close to redesign step 2 eigenmodes 2 and 3 switch, close to redesign step 15 eigenmodes 1 an 2 switch, close to redesign step 16 possible multiple eigenmodes switch, and finally close to redesign step 20 eigenmodes 1 and 2 switch. Although multiple eigenfrequencies are involved a monotone increasing of the first eigenfrequency is found by the OC procedures.

With focus on the case of 20 % material Fig. 7 is a presentation similar to Fig. 3 for the cantilever problem. The initial design, illustrated in Fig. 7a is uniform material density (here ρ e all equal to 0.2). Figure 7b shows the distribution of values of optimality criterion for material distribution OC m for the initial design in Fig. 7a. The positive as well as negative values illustrate that a better material distribution can be obtained by redesign. After 10 redesigns of only material density, the first eigenfrequency is increased with a factor close to 1.5, and Fig. 7c shows the optimized material distribution, when isotropy is kept. Figure 7d shows the distribution of OC m values for the optimized design in Fig. 7c. Note, that these OC m values are almost constant in domains corresponding to active design parameters ρ min <ρ e < ρ max. The white domains correspond to ρ e =ρ min=0.01, to be interpreted as holes.

After 10 more redesigns where the normalized constitutive matrices are also redesigned according to the simple formula (23) with modification (24) the first eigenfrequency is increased further, now with a factor of 2.4. Figure 7e shows the optimized material distribution and is related to a longitudinal eigenmode. Figure 7f shows the distribution of OC m values for the optimized design in Fig. 7e. Also these OC m values are almost constant in domains corresponding to active design parameters ρ min<ρ e <ρ max and the white domains correspond to ρ e =ρ min=0.01. To illustrate the obtained anisotropy (in reality 6 components locally) Fig. 7g shows values for the level of anisotropy, being a number between 1/3 for isotropy and 1 for single directional ”fiber”. As explained in the appendix, the largest normalized stiffness is used to illustrate the level of anisotropy. Figure 7h shows lines of direction for the use of this largest normalized stiffness. Figs. 7e, g and h give a rather good illustration of the final optimized design.

The shown iteration histories in Fig. 8 gives an impression of stable convergence for the chosen numerical procedure (14), with the same numerical control parameters 4.0,0.8, and q=0.8 in (14) and β=0.2 in (24) for all cases. With no fixed design domain, it may be concluded that not only relative but also the absolute largest eigenfrequency is obtained for the smallest amount of material, not unexpected with the larger design possibilities.

Fig. 8
figure 8

Iteration histories for the beam-bridge problem with 20 %, 40 %, 60 % and 80 % of full material

Full size image

6 Conclusion

While many papers in the literature present eigenfrequency optimized by material distribution, examples with eigenfrequency optimization by design of constitutive matrices does not seem available in the literature. The combined problem may be termed eigenfrequency optimization by free material optimization (FMO). In the present paper the essential point for a practical formulation is the separation of anisotropy description from the material distribution.

Local non-dimensional constitutive matrices are constrained to have unit norm of trace and Frobenius. An optimality criterion based on this constraint and stationary eigenfrequency shows that the components of a constitutive matrix are obtained directly from the strain state corresponding to the actual eigenmode. From this follows almost directly that the trace norm is equal to the Frobenius norm, which then may be scaled to unity. The amount of material is the material constraint for the combined optimization.

For the determination of material distribution among the elements of the model, a rather simplified optimality criterion is derived. Size constraints are satisfied iteratively with the amount of material completely satisfied in each iteration. The heuristic procedure for this shows good stability and rapid convergence. The explicit expression for the gradients of eigenfrequency as a function of local material density may at first seem complicated. They are shown to be extremely simple and general, which is believed to be a further major result in the present paper. Proportionality between element stiffness and material density is assumed in the present derivation, but a non-linear interpolation function will only modify the present results slightly, see Pedersen and Pedersen (2012). The resulting simple formula is a product of terms with direct physical interpretation. To clarify the derivation of this formula, a notation for partial derivation in combination with application of the chain rule is applied.

For the two examples with each four different amount of material, rather monotone increasing of the first eigenfrequency by redesign is observed. This includes cases of mode switching and multiple (close to multiple) eigenfrequencies. For these cases alternative formulations, such as objective by sum of eigenfrequencies, is not attempted. Simplicity is preferred, and the method of subspace for determination of several eigenmodes with close or equal eigenfrequencies, is an essential part for problem-free optimization, using the present simple optimality criteria approach.