Exponential penalty function formulation for multilevel optimization using the analytical target cascading framework

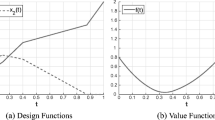
Abstract

An exponential penalty function (EPF) formulation based on method of multipliers is presented for solving multilevel optimization problems within the framework of analytical target cascading. The original all-at-once constrained optimization problem is decomposed into a hierarchical system with consistency constraints enforcing the target-response coupling in the connected elements. The objective function is combined with the consistency constraints in each element to formulate an augmented Lagrangian with EPF. The EPF formulation is implemented using double-loop (EPF I) and single-loop (EPF II) coordination strategies and two penalty-parameter-updating schemes. Four benchmark problems representing nonlinear convex and non-convex optimization problems with different number of design variables and design constraints are used to evaluate the computational characteristics of the proposed approaches. The same problems are also solved using four other approaches suggested in the literature, and the overall computational efficiency characteristics are compared and discussed.

Appendices

Appendix A

Alternative approaches for choosing the penalty parameters are considered, where $a_{\mathrm {ij}}^{\mathrm {k}}=a_{0}$ and $b_{\mathrm {ij}}^{\mathrm {k}} =b_0\; \forall {\mathrm {k}}$ or $a_{\mathrm {ij}}^{{\mathrm {k}}+1} =\beta a_{\mathrm {ij}}^{\mathrm {k}} >a_{\mathrm {ij}}^{\mathrm {k}}$ and $b_{\mathrm {ij}}^{{\mathrm {k}}+1} =\beta b_{\mathrm {ij}}^{\mathrm {k}} >b_{\mathrm {ij}}^{\mathrm {k}} \;\forall {\mathrm {k}}$ with no dependence on values of the multipliers. For this case, $a_{ij}=b_{ij} = 1$ or $a_{\mathrm {ij}}^{{\mathrm {k}}+1} =\beta a_{\mathrm {ij}}^{\mathrm {k}}$ and $b_{\mathrm {ij}}^{{\mathrm {k}}+1} =\beta b_{\mathrm {ij}}^{\mathrm {k}}$ with $\beta = 2$. For the updating approach with dependence on values of the multipliers, $\boldsymbol {\omega }_{ij}^k =\boldsymbol {\omega }_0 =1\;\forall k$ and $\boldsymbol {\nu }_{ij}^k =\boldsymbol {\nu }_0 =1$ as well as $\boldsymbol {\omega }_{ij}^{k+1} =\beta \boldsymbol {\omega }_{ij}^k$ and $\nu _{ij}^{k+1} =\beta \nu _{ij}^k$ with $\beta = 2$. These approaches were applied in the solution to Problem 2 according to EPF I approach. Same initial design point x $^{(0)} = [3, 3, 3, 3, 3, 3, 3]$ was selected for all approaches with $\mu ^{(0)} = 1$ and $\gamma ^{(0)} = 1$.

Results in Table 2 show that for the same level of accuracy, the number of function evaluations and CPU time are generally reduced when the penalty parameters are kept independent of the multipliers. Also, by allowing the penalty parameters to be updated during the optimization process, solution efficiency improves.

Table 2 Comparison of results in Problem 2 with different parameter updating approaches

Appendix B

Problem 3 is solved using three different decompositions. Decomposition 1, as shown in Fig. 13a, consists of two elements, element 11 at the top level and element 22 at the bottom. The target/response variables are $x_{3}$ and $x_{6}$, {$x_{1}$, $x_{2}$, $x_{4}$, $x_{5}$, $x_{7}$} are the local variables for element 11 and {$x_{8}$, $x_{9}$, $x_{10}$, $x_{11}$, $x_{12}$, $x_{13}$, $x_{14}$} are the local variables for elements 2. The objective function is assigned to element 11. The constraints $g_{1}$, $g_{2}$, $h_{1}$, $h_{2}$ are allocated to elements 11 and the others to element 22. Decomposition 2 shown in Fig. 13b also consists of two elements as in the previous case, but the target/response variables are $x_{5}$ and $x_{11}$, {$x_{3}$, $x_{4}$, $x_{8}$, $x_{9}$, $x_{10}$} are the local variables for element 11 and {$x_{2}$, $x_{6}$, $x_{7}$, $x_{12}$, $x_{13}$, $x_{14}$} are the local variables for elements 22. The objective function is decomposed into two parts, $x_1^2$ assigned to element 1 and $x_2^2$ to element 22. The constraints $g_{1}$, $g_{3}$, $g_{4}$, $h_{1}$, $h_{3}$ are allocated to elements 11 and the others to element 22. Decomposition 3 is the three-level hierarchy presented in Fig. 9.

Figure 13

Hierarchical decompositions 1 and 2 of Problem 3

Figure 14 displays the number of function evaluations and the CPU time versus the absolute solution error $e$ for termination tolerances $\tau = 10^{-2}, 10^{-3}, 10^{-4}, 10^{-5}$. The initial values for the penalty parameters in EPF I and EPF II are set to $\mu ^{(0)} = 1$ and $\gamma ^{(0)} = 1$. The starting point for all decompositions is x $^{(0)} = [$5.0, 5.0, 2.76, 0.25, 1.26, 4.64, 1.39, 0.67, 0.76, 1.7, 2.26, 1.41, 2.71, 2.66$]$.

Figure 14

Function evaluations (a) and CPU time (b) versus solution error in Problem 3 for decompositions 1, 2, and 3

The results show that the form of decomposition affects computational efficiency. For all the cases considered, decomposition 1 is more efficient than the other two. Moreover, EPF II (single-loop) is more computationally efficient than EPF I regardless of the decomposition model used. In particular, EPF II for decomposition 1 requires the least number of function evaluations and CPU time whereas EPF I for decomposition 3 requires the most. Comparing the two-level decompositions 1 and 2, it appears that EPF I_1 requires 61 % less function evaluations than EPF I_2, whereas EPF II_1 requires 32 % less function evaluations than EPF II_2. In terms of CPU time, EPF I_1 is 78 % faster than EPF I_2, whereas EPF II_1 is 16 % faster than EPF II_2.