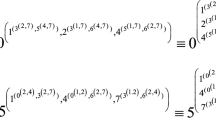1 Introduction

Graph isomorphism identification is a widely used technique in many fields. It can be used in pattern recognition [1, 6], artificial visual sense [4, 8], and molecule isomorphism judgment [2, 11]. Because these problems are of great importance in scientific research and practical application, there are numerous scientists who consider the graph isomorphism issue to be their primary research area [9]. They try to solve the graph isomorphism problem by using various methods in different fields [3, 7, 12, 13].

In our previous work, we proposed a method named circuit simulation (CS), which proved to be efficient in the graph isomorphism problem [10, 14]. Because there are many families of graphs that have specific features, we tested different families to determine whether the CS method is a general algorithm for all cases. We found that there will be failure when it is applied to the graph family called regular graph [5], which is a group of graphs in which each vertex has the same degree.

In this paper, we propose a new method based on the CS method named single-vertex excitation (SVE). The SVE method conducts excitation on one vertex in the graph instead of all the vertices, so it will not be affected by the regularity of the graph degree. It has proven to be valid and efficient in regular graph isomorphism problems in our tests. In Sect. 2, we introduce regular graphs. The details of this algorithm are shown in Sect. 3. Section 4 explores computational complexity, and Sect. 5 displays the performance comparison according to tests.

2 Regular Graph

In graph theory, a finite graph G of size N is an order pair G \(=\) (V, E), which is composed of a finite set of vertices V \(=\) {\(1, 2, 3, {\ldots },\) N} and a set of edges \(E\subseteq V\times V\). The degree of a vertex \(v\) is the number of edges connected to it.

Regular graph, where each vertex has the same degree, is a special type of graph. We can call a regular graph with vertices of degree \(d\) a \(d\)-regular graph. Obviously, the total number of edges in a \(d\)-regular graph of size N is N \(d/2\) because each edge connects two vertices. Thus, \(N\) and \(d\) cannot both be odd at the same time.

We can use the adjacency matrix A \(= [a_{ij}]_{N\times N}\) to represent graph \(G\) concisely.

$$\begin{aligned} a_{ij} =\left\{ {{\begin{array}{l} {1;\quad \hbox {when}\, v_i\, \hbox {and}\, v_j\, \hbox {are} \,\hbox {connected}} \\ {0;\quad \hbox {else}} \\ \end{array} }} \right. \end{aligned}$$

The graph isomorphism problem is equivalent to finding a one-to-one match between vertex sets V \(_{1}\) and V \(_{2}\) in graph G \(_{1}=\) (V \(_{1}\),  E \(_{1}\)) and G \(_{2 }=\) (V \(_{2},\)  E \(_{2}\)). The adjacency matrix can also reflect the isomorphic relationship. G \(_{1}\) and G \(_{2}\) are isomorphic if and only if the adjacency matrix \(A_{2}\) can be converted to \(A_{1}\) through row and column exchanges.

If G is a \(d\)-regular graph of size N, adjacency matrix A will have some special properties. For each \(i,\,\sum \nolimits _{j-1}^N {a_{ij} } =d\). Similarly, for each \(j\), \(\sum \nolimits _{i-1}^N {a_{ij} } =d\).

Such a property increases the difficulty of isomorphism identification because of the high symmetry of regular graphs. In previous research, we proposed the CS method for solving random graph isomorphism problems efficiently, but it cannot be applied in this case. The core of the CS method is to construct a circuit model and solve the node-voltage equation YU \(=\) I to obtain the voltage vector U and match the vertices in two graphs according to it. \(Y=\left[ {y_{ij} } \right] _{N\times N} \) is the admittance matrix and I \(= (1, 1, 1, {\ldots }, 1)^{T}\) is the current excitation.

$$\begin{aligned} y_{ij} =\left\{ \begin{array}{ll} 2\sum \nolimits _{j-1}^N a_{ij} ; &{}\quad \hbox {when}\,\, i=j \\ -a_{ij} ; &{}\quad \hbox {when}\,\, i\ne j \\ \end{array} \right. \end{aligned}$$

When dealing with a regular graph, all of the elements in voltage vector U will be the same, and the result is that we cannot find any correspondence between vertices. It can be demonstrated as follows.

Suppose that G is a \(d\)-regular graph of size N and A is its adjacency matrix. According to the CS method, we next create admittance matrix Y. According to the relationship between A and Y, we can easily obtain Y \(= -\) A \(+ 2d\) P, in which P is an identity matrix of size N.

$$\begin{aligned} \sum _{j-1}^N {y_{ij} } =\sum _{i-1}^N {y_{ij} } =\sum _{j-1}^N {\left( {-a_{ij} } \right) +2d=-d+2d=d} \end{aligned}$$

Thus, for the node-voltage equation,

$$\begin{aligned} \left( {{\begin{array}{cccc} {y_{11} }&{}\quad {y_{12} }&{}\quad \cdots &{}\quad {y_{1N} } \\ {y_{21} }&{}\quad {y_{12} }&{}\quad \cdots &{}\quad {y_{2N} } \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {y_{N1} }&{}\quad {y_{N2} }&{}\quad \ldots &{}\quad {y_{NN} } \\ \end{array} }} \right) \left( {{\begin{array}{c} {V_1 } \\ {V_2 } \\ \vdots \\ {V_N } \\ \end{array} }} \right) =\left( {{\begin{array}{c} {I_1 } \\ {I_2 } \\ \vdots \\ {I_N } \\ \end{array} }} \right) =\left( {{\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array} }} \right) , \end{aligned}$$

apparently, \(V_1 =V_2 =\cdots =V_N =\frac{1}{d}\) is a solution as \(I_i \sum \nolimits _{j-1}^N {y_{ij} } \cdot V_i =\frac{1}{d}\sum \nolimits _{j-1}^N {y_{ij} } =1\).

According to the existence and uniqueness theorems of linear equations, it is the unique solution.

3 The SVE Method

To solve the regular graph isomorphism problem, we propose a new method called SVE based on the CS method. Different from the CS method, we apply only one current source between the vertex \(v\) that we choose and the reference in the circuit model, instead of a complete excitation, which means there is a current source between every vertex and the reference. We call such an operation creating single excitation on vertex \(v\). According to circuit theory and the circuit model that we build, we can solve the node-voltage equation YU \(=\) I for the voltage vector U. We can also obtain the voltage set S after ranking the elements of U from large to small.

For regular graph G and G \(^{\prime }\), we create single excitation on vertex \(v_{i}\) in G and \(v_{j}^{\prime }\) in G \(^{\prime }\) and obtain voltage sets S \(_{i}\) and S \(_{j}^{\prime }\). V \(_{i}\) and \(v_{j}^{\prime }\) are correspondent if and only if S \(_{i} =\) S \(_{j}^{\prime }\). By comparing all of the elements in voltage sets, we can match other vertices in G and G \(^{\prime }\). Due to the high symmetry in regular graph, there may be several identical elements in a voltage set and we cannot obtain a one-to-one match among them. If so, we perform the above operations among these to-be-matched vertices again. By analyzing all of the obtained voltage sets, we can identify the isomorphic relationship between G and G \(^{\prime }\).

The whole process of the SVE method is outlined as follows.

Algorithm 1: Node-voltage Method

Input: the admittance matrices Y of graphs G, the selected vertex v \(_{k}\)

Output: the voltage vector U and the voltage sets S

1 Construct current vector I in which the element of number k is 1, while the others are 0.

2 Solve the circuit equation YU \(=\) I for U.

3 Get the voltage sets S after ranking the elements of U from large to small, respectively.

Algorithm 2: SVE Method

Input: the adjacency matrices (D and D \(^{\prime }\)) of graphs (G and G \(^{\prime }\))

Output: the identification of isomorphic graphs.

1 Get the admittance matrices (Y and Y \(^{\prime }\)) from D and D \(^{\prime }\).

2 Get U \(_{1}\) and S \(_{1}\) on v \(_{1}\) of G by Node-voltage Method.

3 For i \(<\) n \(+ \mathbf{1}\) (n is the number of graph’s vertices, and the initial value of i is 1)

4 Get U \(_{i}\) and S \(_{i}\) on v \(_{i}\) of G \(^{\prime }\) by Node-voltage Method.

5 If S \(_{i} ==\) S \(_{1}\), goto 7.

   Else i \(=\) i \(+\mathbf{1}\).

6 If i \(==\) n \(+ \mathbf{1}\), goto 15.

7 k \(=\) i (v \(_{k}\) matches v \(_{1}\)).

8 Match all asymmetry vertices of G and G \(^{\prime }\) according to S \(_{1}\) and S \(_{k}\).

9 If all the vertices of G and G \(^{\prime }\) all matched, goto 14.

10 Get U \(_{s}\) and S \(_{s}\) on v \(_{s}\) of G by Node-voltage Method. v \(_{s}\) is one of the unmatched vertices with the largest voltage according to S \(_{1}\).

11 Find v \(_{t}\) matching v \(_{s}\) in the unmatched vertices with the largest voltage according to S \(_{k}\). S \(_{t}\) should be the same as S \(_{s}\) (v \(_{t}\) matches v \(_{s}\)). If v \(_{t}\) could not be found, goto 15.

12 Match all asymmetry unmatched vertices of G and G \(^{\prime }\) according to S \(_{s}\), and S \(_{t}\).

13 If all the vertices of G and G \(^{\prime }\) all matched, goto 14.

      Else goto 10.

14 G and G \(^{\prime }\) are isomorphic. End

15 G and G \(^{\prime }\) are not isomorphic. End

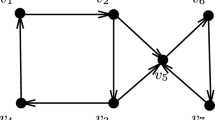
Here is a simple example to better illustrate our method. G and G \(^{\prime }\) are 3-regular graphs of size 8 (Figs. 1,  2).

Fig. 1
figure 1

Graph G

Full size image
Fig. 2
figure 2

Graph G \(^{\prime }\)

Full size image

We can easily obtain adjacency matrixes A and A \(^{\prime }\) as well as admittance matrixes Y and \(Y^{\prime }\).

$$\begin{aligned} A= & {} {\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \\ 8 \\ \end{array} }\left( {{\begin{array}{cccccccc} 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0 \\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1 \\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1 \\ 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right) \\ A^{{\prime }}= & {} {\begin{array}{l} {1^{\prime }} \\ {2^{\prime }} \\ {3^{\prime }} \\ {4^{\prime }} \\ {5^{\prime }} \\ {6^{\prime }} \\ {7^{\prime }} \\ {8^{\prime }} \\ \end{array} }\left( {{\begin{array}{cccccccc} 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1 \\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0 \\ 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right) \\ Y= & {} {\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \\ 8 \\ \end{array} }\left( {{\begin{array}{cccccccc} 6&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad {-1}&{}\quad 0 \\ 0&{}\quad 6&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad {-1} \\ 0&{}\quad {-1}&{}\quad 6&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 0 \\ {-1}&{}\quad 0&{}\quad 0&{}\quad 6&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad {-1} \\ 0&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 6&{}\quad 0&{}\quad {-1}&{}\quad {-1} \\ {-1}&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 6&{}\quad 0&{}\quad 0 \\ {-1}&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 6&{}\quad 0 \\ 0&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad 6 \\ \end{array} }} \right) \\ Y^{\prime }= & {} {\begin{array}{l} {1^{\prime }} \\ {2^{\prime }} \\ {3^{\prime }} \\ {4^{\prime }} \\ {5^{\prime }} \\ {6^{\prime }} \\ {7^{\prime }} \\ {8^{\prime }} \\ \end{array} } \left( {{\begin{array}{cccccccc} 6&{}\quad {-1}&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-1} \\ {-1}&{}\quad 6&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 0 \\ 0&{}\quad {-1}&{}\quad 6&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad {-1} \\ {-1}&{}\quad 0&{}\quad 0&{}\quad 6&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad {-1} \\ 0&{}\quad 0&{}\quad {-1}&{}\quad 0&{}\quad 6&{}\quad {-1}&{}\quad {-1}&{}\quad 0 \\ 0&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad 6&{}\quad {-1}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad {-1}&{}\quad {-1}&{}\quad {-1}&{}\quad 6&{}\quad 0 \\ {-1}&{}\quad 0&{}\quad {-1}&{}\quad {-1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 6 \\ \end{array} }} \right) \end{aligned}$$

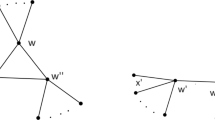
We construct the circuit model as follows when we create single excitation on \(v_{1 }\)in G (Fig. 3).

Fig. 3
figure 3

Circuit model with single excitation on \(v_{1}\) in G

Full size image

Solve the node-voltage equation YU \(_{1 }=\) I \(_{1}\) for U \(_{1}\), in which I \(_{1}= (1 0 0 0 0 0 0 0)^\mathrm{T}\).

We obtain U \(_{1 }= \left( \begin{array}{cccccccc}0.1853&0.0095&0.0087&0.0390&0.0087&0.0390&0.0338&0.0095 \end{array}\right) ^\mathrm{T}\) and S \(_{1 }= \left( \begin{array}{cccccccc}0.1853&0.0390&0.0390&0.0338&0.0095&0.0095&0.0087&0.0087\end{array}\right) ^\mathrm{T}\) after sorting all the elements.

Then, we traverse all of the vertices in G \(^{\prime }\) to create single excitation to find the correspondent vertex of \(v_{1}\). We obtain voltage vector U \(_{i}^{\prime }\) and voltage set S \(_{i}^{\prime }\) when operating on \(v_{i}^{\prime }\).

$$\begin{aligned} {\varvec{U}}_{1}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.1855&0.0344&0.0132&0.0390&0.0050&0.0080&0.0087&0.0396\end{array}\right) ^\mathrm{T}\\ {\varvec{S}}_{1}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.1855&0.0396&0.0390&0.0344&0.0132&0.0087&0.0080&0.0050\end{array}\right) ^\mathrm{T}\\ {\varvec{U}}_{2}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.0344&0.1840&0.0351&0.0095&0.0132&0.0344&0.0095&0.0132\end{array}\right) ^\mathrm{T}\\ {\varvec{S}}_{2}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.1840&0.0351&0.0344&0.0344&0.0132&0.0132&0.0095&0.0095\end{array}\right) ^\mathrm{T}\\ {\varvec{U}}_{3}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.0132&0.0351&0.1840&0.0095&0.0344&0.0132&0.0095&0.0344\end{array}\right) ^\mathrm{T}\\ {\varvec{S}}_{3}^{\prime }= & {} \left( \begin{array}{cccccccc} 0.1840&0.0351&0.0344&0.0344&0.0132&0.0132&0.0095&0.0095\end{array}\right) ^\mathrm{T}\\ {\varvec{U}}_{4}^{\prime }= & {} \left( \begin{array}{cccccccc}0.0390&0.0095&0.0095&0.1853&0.0087&0.0087&0.0338&0.0390\end{array}\right) ^\mathrm{T}\\ {\varvec{S}}_{4}^{\prime }= & {} \left( \begin{array}{cccccccc}0.1853&0.0390&0.0390&0.0338&0.0095&0.0095&0.0087&0.0087\end{array}\right) ^\mathrm{T} \end{aligned}$$

Because S \(_{1}=\) S \(_{4}^{\prime },\,v_{1}\) and \(v_{4}^{\prime }\) can be considered correspondent vertices. We can also conclude that \(v_{7}\) and \(v_{7}^{\prime }\) are correspondent due to the unique voltage 0.0338.

Now, we pay attention to the vertices \(v_{2},\,v_{8}\) in G and \(v_{2}^{\prime },\,v_{3}^{\prime }\) in G \(^{\prime }\), which have the same voltage.

Choose \(v_{2}\) and \(v_{2}^{\prime }\) to create single excitation.

$$\begin{aligned} {\varvec{U}}_{2 }= & {} \left( \begin{array}{cccccccc}0.0095&0.1840&0.0344&0.0132&0.0132&0.0344&0.0095&0.0351\end{array}\right) ^\mathrm{T}\\ {\varvec{S}}_{2 }= & {} \left( \begin{array}{cccccccc} 0.1840&0.0351&0.0344&0.0344&0.0132&0.0132&0.0095&0.0095\end{array}\right) ^\mathrm{T} \end{aligned}$$

S \(_{2} =\) S \(_{2}^{\prime }\) and \(v_{2}\) and \(v_{2}^{\prime }\) are correspondent. We can also conclude that \(v_{8}\) and \(v_{3}^{\prime }\) are correspondent due to the unique voltage 0.0351. So far, we have matched \(v_{1}\) and \(v_{4}^{\prime },\,v_{7}\) and \(v_{7}^{\prime },\, v_{2 }\) and \(v_{2}^{\prime }\), and \(v_{8 }\) and \(v_{3}^{\prime }\).

The remaining vertices are listed.

 

\(v_{3}\)

\(v_{4}\)

\(v_{5}\)

\(v_{6}\)

\(v_{1}^{\prime }\)

\(v_{5}^{\prime }\)

\(v_{6}^{\prime }\)

\(v_{8}^{\prime }\)

Operation1

0.0087

0.0390

0.0087

0.0390

0.0390

0.0087

0.0087

0.0390

Operation2

0.0344

0.0132

0.0132

0.0344

0.0344

0.0132

0.0344

0.0132

Comparing the voltages in operation1 and operation2, we can easily identify the correspondence that \(v_{3}\hbox {--} v_{6}^{\prime }, v_{4}\hbox {--}v_{8}^{\prime },\, v_{5}\hbox {--}\, v_{5}^{\prime }\) and \(v_{6}\hbox {--} v_{1}^{\prime }\).

In conclusion, G and G \(^{\prime }\) are isomorphic, and the vertices’ correspondences are shown as follows:

G

\(v_{1}\)

\(v_{2}\)

\(v_{3}\)

\(v_{4}\)

\(v_{5}\)

\(v_{6}\)

\(v_{7}\)

\(v_{8}\)

G \(^{\prime }\)

\(v_{4}^{\prime }\)

\(v_{2}^{\prime }\)

\(v_{6}^{\prime }\)

\(v_{8}^{\prime }\)

\(v_{5}^{\prime }\)

\(v_{1}^{\prime }\)

\(v_{7}^{\prime }\)

\(v_{3}^{\prime }\)

4 Computational Complexity

Assume that there are n vertices in a regular graph.

The computational complexity of SVE method primarily depends on the following aspects:

  1. (1)

    Obtaining an admittance matrix of a regular graph: \(\varvec{O}(\varvec{n}^{2})\);

  2. (2)

    Solving the node-voltage equation, a set of n equations with n variables, using the generalized minimum residual method (GMRES):\(\varvec{O}(\varvec{n}^{2})\);

  3. (3)

    Finding the first matched vertices by the node-voltage method: \(\varvec{O}(\varvec{n}^{3})\) (It is determined by how to find, and the minimum is \(\varvec{O}(\varvec{n}^{2})\), while the maximum is \(\varvec{O}(\varvec{n}^{3})\));

  4. (4)

    Defining the correspondence of vertices between two regular graphs by comparing the voltage sets: \(\varvec{O}(\varvec{n}^{2})\);

Thus, the time complexity of the SVE method is at the level of \({\varvec{O}(\varvec{n}^{3})}\) (the minimum is \({\varvec{O}(\varvec{n}^{2})}\), and the maximum is \({\varvec{O}(\varvec{n}^{3})}\)).

5 Performance

The following data are used on a PC with an Intel Core i3-2310M CPU (basic frequency is 2.10 GHz) and 3G RAM. Each tested pair of regular graphs is generated randomly, and they are all isomorphic. The figures display average time consumed by 10 different pairs of random regular graphs.

Figure 4 shows the time consumption of a 500-vertex graph with a different degree. It indicates that the time consumed reduces as the degree rises because the graph symmetry gets stronger as the degree rises and there is less disparity when determining the first excitation vertex.

Fig. 4
figure 4

The performance of time-consuming with increasing degree (500-vertex graph)

Full size image

Figure 5 is the comparison of the time consumed between SVE and VF2 for 10 regular graphs with different vertices, and SVE obviously prevails in the time cost. The computation time of SVE is approximately 21 s for a 10-regular graph with 500 vertices, whereas VF2 takes approximately 96 s for a 10-regular graph with 175 vertices. The SVE proved to be efficient in the regular graph problems in the test.

Fig. 5
figure 5

Comparison of SVE and VF2 with variation of the vertices’ numbers (the degree of all regular graphs is 10)

Full size image

6 Conclusion

According to the test results given in Sect. 5, the SVE method is efficient and valid when handling regular graph isomorphism. It could solve the isomorphism problem of regular graphs, and it consumes much less time compared with the traditional algorithms. This method could widen the application range of circuit simulation methods for a regular graph.

The time consumed in finding the first pair of corresponding vertices varies in different situations. To reduce the time consumed, further study based on the properties of regular graphs will be needed to extract its characteristic points. Besides, finding all of the corresponding relationships between the vertices is worth exploring.

In addition, it seems that the SVE method also works for common finite graphs. In the future, the effectiveness and the reliability of the modified method for common graphs will be confirmed, in order to enrich the system of circuit simulation methods.