1 Introduction

Plate boundaries and active faults are commonly segmented, and earthquakes repeatedly occur at each segment. For example, large earthquakes have occurred at recurrence intervals of 90–150 years along the Nankai trough in southwestern Japan, and the source regions of these earthquakes can be divided into five segments (Ishibashi 2004). The fact that earthquakes can recur at a segment has been used in long-term earthquake forecasting (Working Group on California Earthquake Probabilities 2008). However, it is still difficult to predict large earthquakes precisely, due to their complex patterns of occurrence. The recurrence times and rupture areas are variable, due to interactions between fault segments, as demonstrated by numerical simulations (Ward 1996; Rundle et al. 2006; Kato et al. 2007; Aalsburg et al. 2010).

A single-degree-of-freedom spring-block model has previously been applied as a simple model of stick–slip and earthquake cycles; in the present study we attempt to understand the conditions necessary for the occurrence of the unstable slip and physical properties that control earthquake cycles (Gu et al. 1984; Rice and Tse 1986). Simulations of complex earthquake cycles can be performed using a two-degree-of-freedom spring-block model, where two blocks are connected by a spring. Using this model with velocity-weakening friction, Huang and Turcotte (1990) examined the effects of interactions between two blocks on earthquake cycles. By using appropriate model parameters, they successfully used this approach to reproduce earthquake cycles similar to those found along the south central San Andreas fault (California) and in the Nankai trough. Huang and Turcotte (1992) systematically examined the same model, but with spatial heterogeneity of the frictional parameters. They showed that the system generally exhibited chaotic behaviour, except for a few isolated windows of periodic recurrence of earthquakes. As the coupling stiffness increased, the two blocks tended to slip simultaneously, with various recurrence intervals. The transition from periodic to chaotic slip behaviour was achieved through repeated period-doubling bifurcations.

Whilst velocity-weakening friction has been assumed in many models of seismicity, rate- and state-dependent friction laws have also been applied. Whilst there may be a the lack of experimental data available in support of the velocity-weakening friction law, the rate- and state-dependent friction laws well describe several natures of rock friction observed in the laboratory (Marone 1998). A single-degree-of-freedom spring-block model has been used with rate- and state-dependent friction to investigate the details of the sliding behaviour and stability in the system concerned (Rice and Tse 1986; Gu and Wong 1991). Erickson et al. (2008) showed that a single-degree-of-freedom spring-block model exhibits complex slip behaviour when the steady-state friction shows extremely velocity weakening. Ma and He (2001) used a two-degree-of-freedom spring-block model with a rate- and state-dependent friction law to examine complex sliding processes, and found that period-doubling bifurcation occurred for some friction parameters, where large events and small events occurred alternately. Using the same two-block model, He (2003) examined the effects of the spring coupling stiffness on slip patterns; it was found that a higher stiffness tended to generate simpler slip patterns in the periodic recurrence of earthquakes, while more complicated or chaotic slip patterns occurred for a lower stiffness. Yoshida and Kato (2003) used a two-degree-of-freedom spring-block model to examine the interactions between a block with unstable frictional properties and a block with stable or conditionally stable frictional properties, and successfully explained the occurrence of slow earthquakes. In other work, Mitsui and Hirahara (2004) connected five blocks in series in order to simulate complex earthquake cycles along the Nankai trough; the five blocks represented the five segments in which earthquakes have historically taken place. These pioneering studies used multi-block models with rate- and state-dependent friction to examine the complexities of simulated earthquake cycles in general terms. However, they did not examine the complexities of simulated earthquake cycles for a sufficiently wide range of friction parameters, nor did they describe routes to the chaotic behaviour of earthquake cycles.

In a simulation study using an elastic continuum model for a subduction fault and rate- and state-dependent friction, Liu and Rice (2007) examined the slip behaviour of a region with steady-state velocity-weakening frictional properties that interacted with a steady-state velocity-strengthening region. The slip behaviour depended on a parameter W/h*, where W is the width of the steady-state velocity-weakening region and h* is the critical nucleation size for unstable slip. Increasing W/h* caused the slip behaviour to change from decaying oscillation, to periodic aseismic slip oscillation, to aperiodic aseismic oscillation and finally to seismic oscillation. Complex slip behaviour also occurs when the friction parameters are non-uniformly distributed on a fault plane, as demonstrated by Hillers et al. (2006).

Although continuum models provide more accurate descriptions of real fault systems, excessive computation times are needed for the numerical simulations performed using these models to obtain a statistically meaningful number of results for a wide range of model parameters. In the present study, we conduct numerical simulations using a two-degree-of-freedom spring-block model with a rate- and state-dependent friction law. By widely and systematically varying the model parameters, we obtained various slip patterns and organised them in phase diagrams. Using these simulation results, we discuss the origins of the complexities of earthquake cycles and the implications for long-term earthquake forecasting.

2 Model

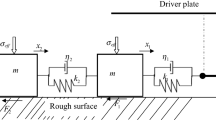
The two-degree-of-freedom spring-block model used in the present study is the same as that used by Yoshida and Kato (2003), except for the evolution law. Two rigid blocks on a frictional floor are connected by a spring of stiffness k 12, and each block is dragged (using a spring of stiffness k 0) by a driver moving at a rate V pl in the x direction (Fig. 1). The equations of motion may be written as

$$ \begin{gathered} {{m_{1} {\text{d}}^{2} x_{1} } \mathord{\left/ {\vphantom {{m_{1} {\text{d}}^{2} x_{1} } {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = k_{0} \left( {V_{\text{pl}} t - x_{1} } \right) + k_{12} \left( {x_{2} - x_{1} } \right) - F_{\text{n}} \mu_{1} , \\ {{m_{2} {\text{d}}^{2} x_{2} } \mathord{\left/ {\vphantom {{m_{2} {\text{d}}^{2} x_{2} } {{\text{d}}t^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{d}}t^{2} }} = k_{0} \left( {V_{\text{pl}} t - x_{2} } \right) + k_{12} \left( {x_{1} - x_{2} } \right) - F_{\text{n}} \mu_{2} , \\ \end{gathered} $$
(1)

where m i , x i , and μ i (i = 1, 2) are the mass, the position coordinate, and the coefficient of friction of the ith block, respectively. The same normal force F n is applied to each of the two blocks.

Fig. 1
figure 1

Schematic diagram of a two-degree-of-freedom spring-block model. Blocks 1 and 2 were connected with a spring of stiffness k 12 and dragged using springs of stiffness k 0 by a driver moving at a constant speed V pl

Full size image

We assume that the frictional stress at the base of each block obeys a rate- and state-dependent friction law (Dieterich 1979; Ruina 1983),

$$ \mu_{i} = \mu_{*} + a_{i} \ln (V_{i} /V_{*} ) + b_{i} \ln (\theta_{i} /\theta_{*} ), $$
(2a)
$$ {{{\text{d}}\theta_{i} } \mathord{\left/ {\vphantom {{{\text{d}}\theta_{i} } {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} = 1 - {{V_{i} \theta_{i} } \mathord{\left/ {\vphantom {{V_{i} \theta_{i} } {L_{i} }}} \right. \kern-\nulldelimiterspace} {L_{i} }}, $$
(2b)

where θ is a state variable, L is a characteristic slip distance, and a and b are constants that represent the rate and time dependence of the friction, respectively. μ * and θ * are the steady-state values at a reference velocity V * , which is chosen to be V pl in the present study. We integrate Eqs. 1, 2a and 2b using a fifth-order Runge-Kutta method with adaptive time-step control (Press et al . 1992).

The differential equation of θ is called the state evolution law, and several types of evolution law have been proposed and used in numerical simulations (e.g., Marone 1998). We used the “aging type” of evolution law (2b) in the present study. The same evolution law was used by Mitsu and Hirahara (2004) and Ohmura and Kawamura (2007). Another popular evolution law is the “slip type”, as expressed by

$$ {{{\text{d}}\theta_{i} } \mathord{\left/ {\vphantom {{{\text{d}}\theta_{i} } {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} = - \left( {{{V_{i} \theta_{i} } \mathord{\left/ {\vphantom {{V_{i} \theta_{i} } {L_{i} }}} \right. \kern-\nulldelimiterspace} {L_{i} }}} \right)\ln \left( {{{V_{i} \theta_{i} } \mathord{\left/ {\vphantom {{V_{i} \theta_{i} } {L_{i} }}} \right. \kern-\nulldelimiterspace} {L_{i} }}} \right), $$
(2c)

This type of state evolution law was used in numerical simulations by Yoshida and Kato (2003), He (2003) and Erickson et al . (2008). Because the sliding behaviour and the condition for the occurrence of unstable slip are different for the two types of state evolution law (Marone 1998; Ranjith and Rice 1999), the simulation results in the present study cannot be directly compared with those using the slip type of the state evolution law.

For a − b < 0, the steady-state friction showed velocity weakening, which can lead to stick–slip motion. For a single-degree-of-freedom spring-block model with a spring stiffness k, the critical stiffness k c is defined to be

$$ k_{\text{c}} = \frac{{\left( {b - a} \right)F_{\text{n}} }}{L}, $$
(3)

and stick–slip occurs for k < k c (Ruina 1983). Note that k c for the two types of the state evolution law are the same. When a − b > 0, the friction shows velocity strengthening, leading to stable sliding. In order to gain an understanding of the interaction between the oscillating blocks, we set a − b < 0 for the two blocks in the present study. The relationship between k and k c is not sufficient to explain the sliding behaviour of a block in the two-degree-of-freedom spring-block system used here. When one block is locked, it is dragged by the other block and the driver; this is equivalent to the block being dragged by a spring of stiffness k 0 + k 12. In this case, unstable slip is expected to occur at the ith block for k 0 + k 12 < k ci , where k ci is the critical stiffness of the ith block, as discussed by Yoshida and Kato (2003). When k 0 > k ci , stable slip occurs at the ith block, whether or not the other block is locked. As discussed by Huang and Turcotte (1992) and He (2003), the stiffness of the coupling spring strongly influences the complexity of the simulated slip patterns. The occurrence of chaotic slip patterns is controlled by the coupling spring. Moreover, it is known that the coupling stiffness significantly affects the statistical properties of simulated earthquakes in models with many degrees of freedom (Brown et al. 1991; Huang et al . 1992).

As discussed above, k 12/k 0, (k 0 + k 12)/k c1 and (k 0 + k 12)/k c2 may be regarded as control parameters in the present two-block model. In our numerical simulation, we fix the values of the loading spring stiffness k 0, the normal force F n and the frictional parameters a and b, whilst varying the coupling spring stiffness k 12 and characteristic slip distance L. We assume that L 1 > L 2, and consequently k c1 < k c2, which indicates that the slip motion of Block 2 is always less stable. The fixed values in the simulations presented herein are as follows: F n = 5.0 × 1018 N, k 0 = 1.0 × 1016 N/m, a 1 = a 2 = 1.0 × 10−3, b 1 = b 2 = 1.2 × 10−3, m 1 = m 2 = 6.0 × 1017 kg, and V pl = 4.0 cm/year; these values fall within the range of those used by Mitsui and Hirahara (2004). They determined the values by considering the actual geometry of the Nankai trough. The masses are calculated using the volumes of the hanging walls of the segments, a constant density of 2.8 × 103 kg/m3, the normal force arising from the applied force on the plate boundary (assuming overburden and hydrostatic pore pressure) and the stiffness from the shear stress due to unit dislocation. The initial conditions in the present simulations are a sliding velocity for the two blocks of V init = 0.001V pl and θ = L/V init. In real fault segments, the coupling stiffness k 12 may qualitatively correspond to the distance between the neighbouring segments, because it represents the increase in shear stress at one block due to unit dislocation at the other. Mitsui and Hirahara (2004) examined the behaviour of blocks for k 12/k 0 = 0.05 and 1.0 and showed that the characteristics observed along the Nankai trough were better reproduced using k 12/k 0 = 1.0. In the present study, we examine the effects of using k 12/k 0 = 0.05, 0.20 and 1.00. We carry out simulations using different initial conditions in order to investigate the effects on the system and find that the statistical steady-state characteristics of the simulation results are the same in all cases.

3 Results

In order to obtain statistical steady-state characteristics in each case, all the simulations are run for a time period of 40,000 years. Simulation results obtained before a statistical steady state is reached are not used in the analyses that follow. We classify the simulated slip patterns into categories from A to H according to their slip velocity and periodicity of simulated slip histories, as shown in Table 1. Seismic slip is defined to be slip with log(V/V pl) > 8, where log(V/V pl) = 8 corresponds to V ~ 0.13 m/s. Slips with rates lower than this are regarded to be aseismic. Slip events with the maximum slip velocity of log(V/V pl) ~ 8 occur infrequently, so changes to the seismic slip threshold value would not significantly have affected the classification of the slip patterns. Where periodicity is found in the simulated slip motion of a block (which may include multiple-cycle oscillations), we regard it to be a periodic oscillation. On the other hand, where no periodicity is found in the oscillating block motion, the oscillation may be regarded to be chaotic. Figure 2 shows phase diagrams for slip patterns for k 12/k 0 = 0.05, 0.20 and 1.00, plotted with axes (k 0 + k 12)/k c2 versus (k 0 + k 12)/k c1, and where each symbol indicates a slip pattern for a single case. As expected theoretically, stable slip (pattern A) occurs for k 0 > k c2 > k c1, regardless of k 12. A decrease in the value of (k 0 + k 12)/k ci causes the slip at the ith block to become unstable. When either k 0 or k 0 + k 12 is close to the critical stiffness for one or two blocks, the system tends to exhibit chaotic behaviour. The examined ranges of (k 0 + k 12)/k c1 and (k 0 + k 12)/k c2 in the simulations are different for different values of k 12/k 0, so that k 0/k c1 = 1.0 and k 0/k c2 = 1.0 are included in both ranges. Example time histories of V and μ − μ * are shown in Figs. 3, 4, 5, 6, 7, 8, 9 and 10 for patterns A–H, where the solid and broken lines respectively indicate the simulated histories for Blocks 1 and 2, and the values of the parameters are shown above each graph. The characteristics of each slip pattern are described in more detail below.

Table 1 Classification of slip patterns of simulation results
Full size table
Fig. 2
figure 2

Phase diagrams of slip patterns on axes of (k 0 + k 12)/k c2 versus (k 0 + k 12)/k c1 for a k 12/k 0 = 0.05, b k 12/k 0 = 0.20, and c k 12/k 0 = 1.00. Symbols A–H stand for the slip patterns classified in Table 1 according to their slip velocity and periodicity of simulated slip. The vertical solid and broken lines represent (k 0 + k 12)/k c1 = 1.0 and k 0/k c1 = 1.0, respectively, and the horizontal solid and broken lines represent (k 0 + k 12)/k c2 = 1.0 and k 0/k c2 = 1.0, respectively. The cases shown in Figs. 3, 4, 5, 6, 7, 8, 9 and 10 are highlighted by red circles

Full size image
Fig. 3
figure 3

Example simulated histories of V for pattern A for a k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 2.100, and (k 0 + k 12)/k c2 = 2.050, and b k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 2.100, and (k 0 + k 12)/k c2 = 1.900. The solid and broken lines show results for Blocks 1 and 2, respectively. Because the slip motion of Block 1 was almost the same as that of Block 2, the solid and broken lines overlap each other

Full size image
Fig. 4
figure 4

Example simulated histories of a, c V and b, d μ − μ * for pattern B for (top) k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 1.900, and (k 0 + k 12)/k c2 = 1.875, and (bottom) k 12/k 0 = 0.20, (k 0 + k 12)/k c1 = 1.075, and (k 0 + k 12)/k c2 = 1.020. The horizontal bars in c and d indicate one period, which includes three and two oscillations at Blocks 1 and 2, respectively

Full size image
Fig. 5
figure 5

Example simulated histories of a, c V and b, d μ − μ * for pattern C for (top) k 12/k 0 = 0.20, (k 0 + k 12)/k c1 = 1.125, and (k 0 + k 12)/k c2 = 0.960, and (bottom) k 12/k 0 = 0.20, (k 0 + k 12)/k c1 = 1.100, and (k 0 + k 12)/k c2 = 0.940. The horizontal bar in each panel represents one period of a multiple cycle

Full size image
Fig. 6
figure 6

Example simulated histories of a, c, e V and b, d, e μ − μ * for pattern D1 for (top) k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 1.050, and (k 0 + k 12)/k c2 = 1.040, and for pattern D2 for (middle) k 12/k 0 = 0.20, (k 0 + k 12)/k c1 = 1.025, and (k 0 + k 12)/k c2 = 1.005, and (bottom) k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 0.800, and (k 0 + k 12)/k c2 = 0.725. The solid and broken horizontal bars in a and b indicate periods α and β, which repeated alternately at the two blocks

Full size image
Fig. 7
figure 7

Example simulated histories of a, c V and b, d μ − μ * for pattern E1 for (top) k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 1.500, and (k 0 + k 12)/k c2 = 0.100, and for pattern E2 for (bottom) k 12/k 0 = 0.20, (k 0 + k 12)/k c1 = 1.010, and (k 0 + k 12)/k c2 = 0.200

Full size image
Fig. 8
figure 8

Example simulated histories of a V and b μ − μ * for pattern F for k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 0.800, and (k 0 + k 12)/k c2 = 0.300

Full size image
Fig. 9
figure 9

Example simulated histories of a V and b μ − μ * for pattern G for k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 0.650, and (k 0 + k 12)/k c2 = 0.640. Time histories of c V and d μ − μ * are shown for the event indicated by arrows in a and b on an expanded time scale

Full size image
Fig. 10
figure 10

Example simulated histories of a, c V and b, d μ − μ * for pattern H for (top) k 12/k 0 = 1.00, (k 0 + k 12)/k c1 = 0.550, and (k 0 + k 12)/k c2 = 0.250, and (bottom) k 12/k 0 = 0.05, (k 0 + k 12)/k c1 = 0.700, and (k 0 + k 12)/k c2 = 0.200. Horizontal bars in c and d indicate one period, which included four and three seismic slip events at Blocks 1 and 2, respectively

Full size image

3.1 Pattern A

When k 0 is larger than k c1 and k c2 (k 0 > k c2 > k c1), the slip motion of the two blocks shows oscillations that decay exponentially, and eventually reaches a stable sliding condition, with V = V pl. Figure 3a shows example time histories of V for pattern A, in which the histories of Blocks 1 and 2 mostly overlapped. The slip motion of Block 1 becomes the same as that of Block 2 after a few oscillations. The characteristic time for exponential decay in the amplitude of the oscillation is longer for smaller values of (k 0 + k 12)/k ci (i = 1 or 2), as shown in Fig. 3b.

3.2 Pattern B

In pattern B, aseismic slip events occur periodically at the two blocks. In contrast with pattern A, the amplitudes of the oscillations in pattern B do not decay with time. In many cases, the two block motions are synchronised (Fig. 4a, b), in which case the coupling spring no longer has any effect because of the constant distance between the two blocks. This results in an apparently smaller spring stiffness for the two blocks, leading to higher slip velocities. Although multiple-cycle oscillation occurs in some cases (Fig. 4c, d), no chaotic oscillation is observed. Multiple-cycle oscillations tend to occur for smaller values of k 12/k 0.

3.3 Pattern C

Pattern C differs from pattern B, in that seismic slip occurs at Block 2. Figure 5a, b shows examples of histories of V and μ − μ * for pattern C, which indicate that a period-4 cycle of aseismic slip events and a period-2 cycle of seismic slip events occur at Blocks 1 and 2, respectively. Here, a period-n cycle signifies that n episodic slip events with different amplitudes and recurrence intervals are included in a single period. For smaller values of (k 0 + k 12)/k ci for i = 1 and 2, the number of cycles is doubled, as shown in Fig. 5c, d, where the period-4 and period-2 cycles for Blocks 1 and 2 become period-8 and period-4 cycles, respectively. No further period-doubling bifurcations are observed in pattern C. Pattern C does not appear for k 12/k 0 = 1.00. This is probably because seismic slip at Block 2 sometimes triggers seismic slip at Block 1 for k 12/k 0 = 1.00, leading to pattern E1, while seismic slip at Block 2 does not promote seismic slip at Block 1 for smaller values of k 12/k 0.

3.4 Pattern D

In pattern D, both seismic and aseismic slip events occur at the two blocks. In contrast to patterns B and C, both periodic and chaotic oscillations may be seen in pattern D. Pattern D is subdivided into patterns D1 and D2, which characterise periodic and chaotic oscillations, respectively. Figure 6a, b shows examples of histories of V and μ − μ * for pattern D1. Note that the solid and broken lines overlap in Fig. 6a when seismic slip events occur simultaneously at Blocks 1 and 2. The slip behaviour of Block 1 during period α (indicated by a horizontal bar in Fig. 6a) is similar to that of Block 2 during period β, and vice versa. This slip pattern is observed only for k 12/k 0 = 1.00. Examples of histories of V and μ − μ * for chaotic oscillations in pattern D2 are shown in Fig. 6c, d. Both the time intervals between successive slip events, and the event amplitudes at Blocks 1 and 2, are highly variable, and no periodicity is found. In some cases, we find that the oscillations change from chaotic (pattern D2) to periodic (pattern D1) in simulations longer than 40,000 years, suggesting the possibility that some of the pattern D2 data in Fig. 2 can change to pattern D1 data if longer simulation times are used. The transition boundary between patterns D1 and D2 in Fig. 2 is therefore not clearly defined. Other simulation results for pattern D2 (see Fig. 6e, f) show that pattern D2 occurs even under unstable conditions (k 0 + k 12 < k c1 < k c2). Although k 0 + k 12 is smaller than k c1 and k c2 in this case, aseismic slip events can occur during an interval between seismic slip events. Pattern D2 was not observed for k 12/k 0 = 0.05.

3.5 Pattern E

In pattern E, both aseismic and seismic slip events are observed at Block 1, while only seismic slip events occur at Block 2. As for pattern D, periodic and chaotic oscillations may be observed in pattern E, which we classify into E1 and E2, respectively. Figure 7a, b shows examples of simulation results for pattern E1, where a period-6 cycle and a period-4 cycle are observed at Blocks 1 and 2, respectively, as indicated by the horizontal bars. At Block 1, the slip becomes seismic when the two blocks slipped simultaneously. Yoshida and Kato (2003) observed a similar slip pattern in the two-block system for k 12/k 0 = 2.0, k 0 + k 12 > k c1 and k 0 + k 12 < k c2, and discussed the mechanism of episodic aseismic slip events (slow earthquakes). Example histories of V and μ − μ * are shown in Fig. 7c, d for pattern E2. As for pattern D, the oscillations sometimes changes from chaotic (pattern E2) to periodic (pattern E1) at longer simulation times. Again, the transition boundary between patterns E1 and E2 in Fig. 2 is not clearly defined, like the boundary between D1 and D2.

3.6 Pattern F

Pattern F is characterised by chaotic earthquake (seismic slip) behaviour, without aseismic slip events. Figure 8a, b shows examples of histories of V and μ − μ * for pattern F, where the recurrence interval and peak slip velocity are variable. Block 2 earthquakes always preceded Block 1 earthquakes, and the time interval between Block 2 and Block 1 earthquakes is variable, as discussed in the section "Recurrence patterns of chaotic slip behaviour". We carry out simulations for a time period of 140,000 years for some pattern F cases to confirm the persistence of chaotic oscillation. Pattern F is observed only for k 12/k 0 = 1.00.

3.7 Pattern G

In pattern G, seismic slip events occur successively at the two blocks with a time delay of less than 1 year. The recurrence interval, the peak slip velocity and the order of the slip events are variable. When the time interval between successive earthquakes at Blocks 1 and 2 is always less than 1 year, we regard this slip behaviour to be of pattern G. Figure 9a, b shows examples of histories of V and μ − μ * for pattern G. Although these histories appear to be periodic, closer inspection shows that V and μ − μ * are variable during interseismic periods. Figure 9c, d shows time histories of V and μ − μ * for the event indicated by the arrows in Fig. 9a, b, using an expanded time scale. Seismic slip first occurs at Block 2, which increases the shear stress at Block 1, triggering seismic slip at Block 1 after a short delay (of about 0.1 year after the Block 2 slip). Block 2 then slips again, after a much shorter delay (of about 0.01 year after the Block 1 slip). Whether it is Block 1 or Block 2 that is the first to be subject to seismic slip is an entirely random matter. The time interval between successive slip events is variable and ranged from 0.003 to 0.22 years. Similar quasi-periodic stick–slip behaviour was observed by He (2003) in a numerical simulation with weak heterogeneity in the friction parameters. Pattern G occurs when the value of k c1 is close to that of k c2, and only when k 12/k 0 = 1.00.

3.8 Pattern H

In pattern H, seismic slip events occur periodically at the two blocks. Figure 10a, b shows a single-period oscillation. As the difference between (k 0 + k 12)/k c1 and (k 0 + k 12)/k c2 increases, period-doubling bifurcation occurs, as discussed in the section "Chaotic slip behaviour and period-doubling bifurcation". When k 12/k 0 = 1.00, the recurrence interval of Block 1 earthquakes is the same as that of Block 2 earthquakes. In cases with weaker interactions (k 12/k 0 = 0.20 and 0.05), as the difference in L between the two blocks increases, periodic oscillations with different periods are observed between the two blocks. Figure 10c, d shows an example of a multiple-cycle oscillation in pattern H, where the horizontal bars indicate a period-4 cycle and a period-3 cycle at Blocks 1 and 2, respectively. The occurrence of multiple-cycle oscillations is consistent with previous results from numerical simulations with strong heterogeneity in the friction parameters (He 2003).

Finally, we summarise the effect of the coupling stiffness k 12/k 0 on the slip pattern. As shown in Fig. 2, the distribution of slip patterns in the case of k 12/k 0 = 1.00 is more complicated than that for k 12/k 0 = 0.20 and 0.05. In the unstable regime in particular (k 0 + k 12 < k c1 < k c2), several slip patterns are observed for k 12/k 0 = 1.00, while pattern H is seen in most regions of the unstable regime for k 12/k 0 = 0.20 and 0.05. As k 12/k 0 decreases, the slip behaviour of the two blocks becomes simpler, and the chaotic slip pattern finally disappears altogether. The recurrence intervals of the simulated slip events in the two-block system are close to those for a one-block system for small k 12/k 0 (which is equivalent to k 12 = 0). We conducted additional simulations for k 12/k 0 = 5.0 and 10.0 and confirmed that chaotic slip patterns occurred for a wider range of parameters. As k 12/k 0 increased, the parameter range of pattern H narrowed, and those of patterns F and G widened. This effect of the coupling stiffness is consistent with that described by Huang and Turcotte (1992), as we discuss below.

4 Discussion

4.1 Chaotic Slip Behaviour and Period-Doubling Bifurcation

We find that the slip behaviour of the two blocks alters as a function of (k 0 + k 12)/k c1 and (k 0 + k 12)/k c2. Here we discuss the details of how this transition occurs. Figure 11 shows a bifurcation diagram for the slip amplitudes of seismic and aseismic slip events at Block 1 for 0.2 ≤ (k 0 + k 12)/k c2 ≤ 0.8, where k 12/k 0 and (k 0 + k 12)/k c1 are fixed at 1.00 and 0.800, respectively. We record events at Block 1 with peak slip velocities greater than V pl, and also measure the slip amplitude for each event. As (k 0 + k 12)/k c2 decreases, the slip behaviour changes from chaotic oscillation including both aseismic and seismic slip events (pattern D2), to periodic seismic slip (pattern H), to chaotic oscillation (pattern F and E2), as shown in Fig. 11. A wide variety of slip amplitudes is observed for D2, F and E2. At (k 0 + k 12)/k c2 ~ 0.50, a period-doubling bifurcation occurs; a single cycle oscillation splits in two, producing a period-2 cycle. With further decreases in (k 0 + k 12)/k c2 similar bifurcations occur repeatedly, until the period of the oscillations diverges to infinity and the system becomes chaotic. Figure 12 shows iteration maps for the recurrence intervals of slip events at Blocks 1 (left) and 2 (right) for the three slip patterns D2, E2 and F; the inter-event time T n between the nth and (n + 1)th events is plotted against the inter-event time T n−1 between the (n − 1)th and nth events, for each simulation run of 100,000 years. The data are distributed widely and randomly for pattern D2, and converged to give simple curves for pattern F. Pattern E2 shows characteristics that are intermediate between D2 and F. The iteration maps for pattern F are similar to those for deterministic chaos led by a period-doubling sequence, as observed for various nonlinear systems (Strogatz 1994). In contrast, the rather random characteristics of patterns D2 and E2 may be related to the different origins of the observed chaotic behaviour. The aseismic slip events in patterns D2 and E2 complicate the slip behaviour, leading to a wide variety of slip amplitudes (Fig. 11) and a wide variety of distributed characteristics in the iteration maps (Fig. 12). A transition in slip behaviour from stable sliding to limit cycle oscillations is symptomatic of Hopf bifurcation (Gu et al . 1984), and the fact that both seismic and aseismic slip events are present suggests that patterns D2 and E2 may be related to this phenomenon (Wechselberger 2005). In contrast to pattern F, such chaotic slip behaviour appears suddenly in the bifurcation diagram, without the period-doubling sequences that have been observed in, for instance, numerical studies of oscillating chemical reactions (Petrov et al . 1992), and the van der Pol equation (Itoh and Murakami 1994; Koper 1995).

Fig. 11
figure 11

Bifurcation diagram of slip amplitudes for seismic and aseismic slip events at Block1 as a function of (k 0 + k 12)/k c2. k 12/k 0 and (k 0 + k 12)/k c1 are fixed at 1.00 and 0.800

Full size image
Fig. 12
figure 12

Iteration maps of recurrence intervals of seismic and aseismic slip events at a, c, e Block1 and b, d, f Block 2, where T n denotes the time interval between nth and (n + 1)th events, for (top) pattern D2, (middle) pattern E2, and (bottom) pattern F. The parameters for the cases in the top, middle and bottom panels were the same as those for Fig. 6 (middle), Fig. 7 (bottom) and Fig. 8, respectively

Full size image

In order to gain an understanding of the rather complicated slip behaviour, we compare the phase portraits of V and μ − μ * for patterns D2, E2 and F (Fig. 13). In pattern D2, an abrupt increases in V and μ − μ * are observed at one block due to occurrences of episodic slip at the other block. When the increased values of (V, μ − μ *) are well above the steady-state line μ ss − μ * = (a − b) ln (V/V pl), the slip accelerates to become seismic, as discussed by Gu et al. (1984). On the other hand, when the increased values of (V, μ − μ *) are around or below the steady-state line, seismic slip is not triggered. Thus, the response of a block to a sudden increase in stress produced by seismic slip at the other block is variable, depending on the stress amplitude and the values of V and μ − μ * at that time, causing complex slip behaviour to occur. It is interesting to note that a higher shear stress before the seismic slip leads to a lower residual stress afterwards, due to dynamic overshoot. This causes variations in the magnitudes of the stress drops and accordingly in the recurrence intervals of the slip events. These factors also make the slip patterns more complicated. For pattern E2, the relationship between V and μ − μ * for Block 2 is simpler because the slip events are always seismic, due to the small (k 0 + k 12)/k c2 values. Because the (V, μ − μ *) values are always far from (V, μ − μ *) = (V pl, 0), aseismic slip events hardly occur. For pattern F, slip events at Blocks 1 and 2 are always seismic, and Block 2 events always precede Block 1 events, as shown in Fig. 9c, d. Seismic slip at Block 2 increases the shear stress at Block 1, which causes variations in both the peak stress before seismic slip and the stress drop at Block 1, which in turn leads to complex slip patterns at Block 1. In contrast, seismic slip at Block 1 occurs when the shear stress at Block 2 is much lower than the critical stress; accordingly, slip at Block 2 is not triggered immediately and the variation of peak stress at Block 2 is smaller. The difference between the phase portrait complexity of patterns D2 and F (Fig. 13) seems to correspond to the difference in complexity in the iteration map (Fig. 12), suggesting that the occurrence of both seismic and aseismic slip events generates more complex slip patterns.

Fig. 13
figure 13

Phase portraits of V and μ − μ * at a, c, e Block 1 and b, d, f Block 2 for patterns (top) D2, (middle) E2 and (bottom) F. The parameters for the cases in top, middle and bottom panels were the same as those for Fig. 6 (middle), Fig. 7 (bottom) and Fig. 8, respectively. Broken and solid lines show log(V/V pl) = 8 (threshold for seismic slip) and μ − μ *  = (a − b)ln(V/V pl) (steady-state friction), respectively

Full size image

Huang and Turcotte (1992) found a period-doubling route to chaos in a two-block model with velocity-weakening friction, where only seismic slip events occurred. They showed that a two-block system with spatially heterogeneous friction generally exhibited chaotic behaviour, with the exception of a few isolated windows of periodic behaviour. In their study, chaotic slip behaviour occurred over wider parameter ranges for higher coupling stiffnesses. In the present model, chaotic slip behaviour is observed for narrower parameter ranges with rate- and state-dependent friction than with velocity-weakening friction. This probably results from the fact that for rate- and state-dependent friction, the shear stress changes to dynamic friction (which is weakly dependent on slip velocity) during seismic slip, while a significant heterogeneity of residual stress is generated just after seismic slip due to the self healing brought about by velocity-weakening friction, as discussed by Cochard and Madariaga (1994).

Using a two-block model with a rate- and state-dependent friction law, He (2003) found that complicated or chaotic slip behaviour occurred for some parameter values. Although He (2003) examined the slip behaviour for narrower ranges of parameters than those used in the present study, he reported that the slip behaviour tended to be chaotic for smaller coupling stiffnesses. Periodic oscillation may be expected to occur for k 12 → 0 and k 12 → ∞, because the two block system is equivalent to the one block system in these extreme cases. The definition given for coupling stiffness by He (2003) was different from ours, and his coupling stiffnesses covered a higher range of values. We therefore expect that simple periodic oscillation would appear again for weaker coupling stiffnesses in He’s model. Moreover, He (2003) used the “slip type” state evolution law, while we used the “aging type”. Ranjith and Rice (1999) studied the stability of quasi-static frictional slip of a single-degree-of-freedom spring block model and showed that the block motion tends to be more unstable for the “slip type” state evolution law than the “aging type” under rapid loading, though the two types of evolution law have the same critical stiffness. The quantitative difference between the present result and He (2003) partly comes from the difference in the state evolution law.

Ruina (1983) and Gu et al. (1984) theoretically investigated the slip motion of a single-degree-of-freedom spring-block model with rate- and state-dependent friction laws. In numerical simulations with two-state variable friction, they found that period-doubling bifurcations leading to chaotic slip motion occurred when the spring stiffness was close to the critical stiffness, although only periodic slip motion was observed for one-state variable friction. Nonlinear dynamic systems of order three or higher are known to generate chaotic behaviour. These findings indicate that it is reasonable that the two block system with one state variable rate- and state-dependent friction used in the present model exhibited chaotic motion.

4.2 Recurrence Patterns of Chaotic Slip Behaviour

Since an understanding of the recurrence patterns of earthquakes is important for long-term earthquake forecasting, we examine the chaotic recurrence patterns of the simulated slip events. Figure 14 shows the simulated histories of cumulative displacement at Block 1 for patterns D2, E2 and F. The two parallel broken lines represent displacements with a constant rate of V pl. If an earthquake occurs when the curve reaches the lower broken line, the slip pattern obeys the time-predictable model. Meanwhile, if the cumulative displacement reaches the upper broken line during an earthquake, it obeys the slip-predictable model (Shimazaki and Nakata 1980). The cumulative displacements in the present model seem to be better explained by the time-predictable model. As shown in Fig. 14, when seismic slip occurs simultaneously at Blocks 1 and 2, the slip amplitude became larger (as indicated by arrows), and the time interval before the next earthquake tends to be longer. This variability of the seismic slip amplitude may have been one of the reasons why the cumulative displacements did not obey the slip-predictable model. Note that aseismic slip events (indicated by the horizontal bars in Fig. 14a, b) do not obey the time-predictable model; this is because these events occur at lower shear stresses. In patterns G and H, both the time-predictable and the slip-predictable models approximately explain the simulated slip histories, because the variance of the recurrence intervals and the slip amplitudes is small.

Fig. 14
figure 14

Example time histories of cumulative displacements at Block 1 for patterns a D2, b E2, and c F, where cumulative displacements at 40,000 years are set to zero. The parameters for a, b and c were the same as those for Fig. 6 (middle), Fig. 7 (bottom) and Fig. 8, respectively. Two parallel broken lines represent displacements with a constant rate of V pl. Horizontal bars indicate periods during which aseismic slip events occurred. Arrows indicate slip events where the two block slipped simultaneously

Full size image

Shimazaki and Nakata (1980) examined historical earthquakes and geomorphological data at three sites in Japan, including the source area of the Nankai earthquakes, and found that estimated slip patterns were approximated rather well by the time-predictable model. This observation is consistent with our results obtained from simulations using rate- and state-dependent friction. Shimazaki (2002) examined simulation results from the two block system with velocity-weakening friction used by Huang and Turcotte (1990), and found that the simulated slip patterns were better approximated by the time-predictable model than the slip-predictable model, suggesting that the time-predictable model may be more useful for long-term earthquake forecasting.

Figure 15 shows the probability density functions for the recurrence intervals of the simulated seismic and aseismic slip events obtained from slip patterns D2, E2 and F. Long-term earthquake forecasts are made using the probability density functions of the recurrence intervals of past earthquakes (Earthquake Research Committee 2001; Working Group on California Earthquake Probabilities 2008). In these probabilistic forecasts, the Brownian Passage Time (BPT) distribution is widely used in view of its superiority in terms of its agreement with observed data and its performance for times much longer than the average recurrence time (Matthews et al . 2002). In Fig. 15, the best-fit BPT distribution is shown by a broken line for each case. \( \bar{T} \) is the average of the recurrence intervals, and α is a parameter of the BPT distribution that is equal to the standard deviation divided by the average of the recurrence intervals. Generally speaking, the BPT distribution fails to explain the distributions of the simulated recurrence intervals. It is especially difficult to explain the significant peaks in the distributions for Block 1 in pattern E2 (Fig. 15c) and for Blocks 1 and 2 in pattern F (Fig. 15e, f) using the BPT distribution. There is a large variation in α, which indicates a large variation in aperiodicity. Aseismic slip events are included in the probability density functions for Blocks 1 and 2 in pattern D2, and for Block 1 in pattern E2 (Fig. 15c, d). By eliminating aseismic slip events, we examine the recurrence intervals of simulated earthquakes for patterns D2 and E2. In pattern D2, significant peaks exist at ~110 years both for Blocks 1 and 2 (Fig. 16a, b). Several peaks for recurrence intervals at ~130, 210, 360 and 520 years are found in the distribution for Block 1 in pattern E2. The values of \( \bar{T} \) and α for the recurrence intervals of simulated earthquakes are 331.67 and 1.46 for Block 1 in pattern D2 (corresponding to Fig. 15a), 143.72 and 1.80 for Block 2 in pattern D2 (corresponding to Fig. 15b) and 211.98 and 0.65 for Block 1 in pattern E2 (corresponding to Fig. 15c). It is interesting to note that these recurrence intervals are much longer than those obtained when aseismic slip events are included, because some aseismic slip events may be included during an interseismic period, as shown in Figs. 6 and 7. Aseismic slip events are partly responsible for the release of accumulated strain, thereby elongating the recurrence intervals between earthquakes. The poor fit of the BPT distribution to the present simulation results may have resulted from the low number of degrees of freedom in the present model. In continuum models with many interacting fault segments, the BPT distribution or the Weibull distribution can explain simulated earthquake recurrence quite well (e.g., Rundle et al . 2006; Kato et al . 2007; Zöller and Hainzl 2007).

Fig. 15
figure 15

Frequency distributions of recurrence intervals of seismic and aseismic slip events at a, c, e Block 1 and b, d, f Block 2 for patterns (top) D2, (middle) E2 and (bottom) F. Broken lines indicate the best-fit BPT distributions, fitted with the parameters \( \bar{T} \) and α. The parameters for the cases in the top, middle and bottom panels were the same as those for Fig. 6 (middle), Fig. 7 (bottom) and Fig. 8, respectively

Full size image
Fig. 16
figure 16

Frequency distributions of recurrence intervals of seismic events at a Block 1 and b Block 2 for pattern D2, and c Block 1 for pattern E2. Broken lines indicate the best-fit BPT distributions, fitted with the parameters \( \bar{T} \) and α

Full size image

Simulated earthquakes do not always occur simultaneously at the two blocks. In pattern F, simulated earthquakes at Block 2 always precede those at Block 1. Figure 17a shows a schematic diagram of the simulated histories of μ − μ * at Blocks 1 and 2, where t1 n and t2 n are the occurrence times of the nth earthquakes at Blocks 1 and 2, respectively. The frequency distributions of time intervals t1 n  – t2 n and t2 n  – t1 n−1 are shown in Fig. 17b. The delay time from successive Block 2 to Block 1 events ranges from 0.6 to 40 years, and the frequency here shows a significant peak in intervals of less than 1 year. A similar feature was previously observed in earthquakes along the Nankai trough. Large earthquakes in the eastern segment (Tonankai earthquakes) have always preceded large earthquakes in the western segments (Nankai earthquakes) in historical sequences of earthquakes in which the two segments were not broken simultaneously; the delay times ranged from 30 h to 2 years (Ishibashi 2004). Figure 17c shows the frequency distribution of the time intervals between successive earthquakes at Blocks 1 and 2 in pattern G, where the time interval between a Block 1 earthquake and a Block 2 earthquake is taken to be positive. The distribution is nearly symmetric about zero delay, and earthquakes at the two blocks generally occur within ~0.2 years. This is probably due to the higher coupling stiffness and nearly symmetric friction parameters in pattern G (Fig. 2c).

Fig. 17
figure 17

a Schematic diagram of histories of μ − μ * at Block 1 (solid line) and Block 2 (broken line). t1 n and t2 n indicate the occurrence times of the nth slip events at Blocks 1 and 2, respectively. b Frequency distributions of time intervals between successive slip events for pattern F at Block 2 to Block 1 (solid line) and Block 1 to Block 2 (broken line). The parameters were the same as those for Fig. 8. c Frequency distributions of time intervals between earthquakes in pattern G, where each time interval was measured from Block 1 earthquake to Block 2 earthquake. The parameters were the same as those for Fig. 9

Full size image

Maps of time intervals t2 n  – t1 n−1 versus t1 n−1 – t2 n−1 and t1 n  – t2 n versus t2 n  – t1 n−1 are shown in Fig. 18a, b, respectively. These maps are expressed by simple curves, as well as iteration maps of recurrence intervals (Fig. 12e, f). Since t2 n  – t1 n−1 and t1 n  – t2 n are multivalued functions of t1 n−1 – t2 n−1 and t2 n  – t1 n−1, respectively, these values are not uniquely determined. However, the simple curves suggest that the occurrence time of the next event in these chaotic earthquake sequences can be predicted to some extent.

Fig. 18
figure 18

Mapping of time intervals between successive slip events for pattern F. a t2 n  – t1 n−1 versus t1 n−1 – t2 n−1. b t1 n  – t2 n versus t2 n  – t1 n−1. The parameters were the same as for Fig. 8

Full size image

5 Conclusions

We simulate the dynamic slip motion of fault segments that interact with each other using a two-degree-of-freedom spring-block model with a rate- and state-dependent friction law. By examining slip behaviour for wide ranges of model parameters, we classify it into several slip patterns according to the slip velocities of episodic events and the periodicity of those events. We find that chaotic slip patterns occurred in some cases, with a period-doubling route to chaotic behaviour. The range of parameters within which chaotic slip patterns are generated seems to be narrower in the present model than that it is in velocity-weakening friction models. The chaotic slip behaviour that occurs with only seismic slip events appears to be different from that which occurs with both seismic and aseismic slip events, as indicated by bifurcation diagrams and iteration maps. The latter type of event has not been reported previously for seismicity models, because most of the existing models do not take aseismic sliding into account. The observed sequences of actual earthquakes commonly show periodicity with large variations. These observed characteristics are similar to the chaotic slip behaviour obtained in the present simulation. We observe chaotic behaviour in a nonlinear system with only two interacting blocks. Although the spring-block system may be too simple to simulate the slip behaviour in an interacting fault system, chaotic slip behaviour is expected to appear in higher order systems in the Earth, where many fault segments interact. It is notable that the physical meaning of stiffness is not necessarily clear in the corresponding fault system in an elastic continuum. Careful consideration of this uncertainty is required if the present simulation results are to be applied to real fault systems.

While velocity-weakening friction models cannot simulate aseismic sliding, the present rate- and state-dependent friction model reproduces the occurrence of aseismic slip events, which have been detected at many subduction zones, including the Nankai trough (Ozawa et al . 2002; Miyazaki et al . 2006). Similarly as reported by Yoshida and Kato (2003), episodic aseismic slip events are observed in the present model. Yoshida and Kato (2003) showed that episodic aseismic slip events occur when the spring stiffness is close to the critical stiffness for unstable slip, though they did not find chaotic slip behaviour in their case. In the present study, chaotic slip patterns sometimes appeared when the spring stiffness is close to the critical stiffness. In some cases, seismic and aseismic slip events occurred randomly at a block. It has been suggested that the 1605 Keicho earthquake along the Nankai trough was a tsunami earthquake, though the other great historical earthquakes along the Nankai trough are thought to be ordinary earthquakes, with significant damage resulting from seismic waves (Ishibashi 2004). This changeable slip behaviour may be explained by the present model.

Chaotic slip behaviour does not automatically preclude the predictability of earthquakes. In the present study, the probability density function of recurrence intervals can be obtained even for chaotic slip patterns; we suggest that probabilistic earthquake forecasting is therefore possible. Moreover, the iteration maps of the inter-event times suggest that a simple structure underlies the chaotic slip patterns. Using these properties, the occurrence time of the next earthquake can be predicted to some extent from past earthquake sequences. In the present model, accelerating aseismic sliding precedes each earthquake, similarly to simpler single-degree-of-freedom spring block models (Roy and Marone 1996; Kato and Tullis 2003). Although the detection of preseismic sliding has not been fully realised, it has the potential to be used for the prediction of earthquakes with chaotic slip patterns.