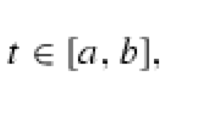Abstract
We study general (not necessarily Hamiltonian) first-order symmetric systems \({J y'-B(t)y=\Delta(t) f(t)}\) on an interval \({\mathcal{I}=[a,b \rangle}\) with the regular endpoint a. It is assumed that the deficiency indices \({n_{\pm}(T_{\rm min})}\) of the minimal relation \({T_{\rm min}}\) satisfy \({n_{+}(T_{\rm min})\leq n_{-}(T_{\rm min})}\). We define special \({\lambda}\)-depending boundary conditions with Nevanlinna-type spectral parameter \({\tau=\tau(\lambda)}\) at the singular endpoint b. With boundary value problem involving such conditions, we associate an exit space self-adjoint extension \({\tilde{T}}\) of \({T_{\rm min}}\) and the \({N \times N}\)-matrix m-function \({m(\cdot)}\) of the size \({N={\rm dim ker} (iJ+I)}\). The role of \({m(\cdot)}\) is similar to that of the Weyl function for a Hamiltonian system. Using the m-function, we obtain the eigenfunction expansion with \({N \times N}\)-matrix spectral function \({\Sigma(\cdot)}\). Moreover, we represent \({\Sigma(\cdot)}\) immediately in terms of a boundary parameter \({\tau}\). We also characterize certain spectral properties of the extension \({\tilde{T}}\). Application of these results to ordinary differential operators of an odd order enables us to complete the results by Everitt and Krishna Kumar on the Titchmarsh–Weyl theory of such operators.
Similar content being viewed by others
References
Albeverio S., Malamud M.M., Mogilevskii V.I.: On Titchmarsh–Weyl functions and eigenfunction expansions of first-order symmetric systems. Integr.Equ. Oper. Theory 77, 303–354 (2013)
Atkinson F.V.: Discrete and Continuous Boundary Problems. Academic Press, New York (1963)
Behrndt J., Hassi S., de Snoo H., Wiestma R.: Square-integrable solutions and Weyl functions for singular canonical systems. Math. Nachr. 284(11-12), 1334–1383 (2011)
Derkach V.A., Hassi S., Malamud M.M., de Snoo H.S.V.: Generalized resolvents of symmetric operators and admissibility. Methods Funct. Anal. Topol. 6(3), 24–55 (2000)
Derkach V.A., Malamud M.M.: Generalized resolvents and the boundary value problems for Hermitian operators with gaps. J. Funct. Anal. 95, 1–95 (1991)
Dijksma A., Langer H., de Snoo H.S.V.: Eigenvalues and pole functions of Hamiltonian systems with eigenvalue depending boundary conditions. Math. Nachr. 161, 107–153 (1993)
Dunford N., Schwartz J.T.: Linear Operators. Part 2. Spectral Theory. Interscience Publishers, New York-London (1963)
Everitt W.N., Krishna Kumar V.: On the Titchmarsh–Weyl theory of ordinary symmetric differential expressions 1: the general theory. Nieuw Arch. voor Wiskd. 24(3), 1–48 (1976)
Everitt W.N., Krishna Kumar V.: On the Titchmarsh–Weyl theory of ordinary symmetric differential expressions 2 : the odd-order case. Nieuw Arch. voor Wiskd. 24(3), 109–145 (1976)
Fulton Ch.T.: Parametrizations of Titchmarsh’s \({m(\lambda)}\)-functions in the limit circle case. Trans. Am. Math. Soc. 229, 51–63 (1977)
Gohberg, I., Krein, M.G.: Theory and applications of Volterra operators in Hilbert space. In: Transl. Math. Monographs, vol. 24. Am. Math. Soc., Providence (1970)
Gorbachuk M.L.: On spectral functions of a differential equation of the second order with operator-valued coefficients. Ukr. Mat. Zh. 18(2), 3–21 (1966)
Gorbachuk V.I., Gorbachuk M.L.: Boundary Problems for Differential-Operator Equations. Kluver Acad. Publ., Dordrecht (1991). [Russian edition: Naukova Dumka, Kiev (1984)].
Hinton D.B., Shaw J.K.: Parameterization of the \({M(\lambda)}\) function for a Hamiltonian system of limit circle type. Proc. R. Soc. Edinb Sect. A 93(3–4), 349–360 (1982/83)
Hinton Schneider D.B., Hinton A.: On the Titchmarsh–Weyl coefficients for singular S-Hermitian systems I. Math. Nachr. 163, 323–342 (1993)
Hinton D.B., Schneider A.: Titchmarsh–Weyl coefficients for odd order linear Hamiltonian systems. J. Spectr. Math. 1, 1–36 (2006)
Hinton D.B., Schneider A.: On the spectral representation for singular selfadjoint boundary eigenfunction problems. In: Oper. Theory: Advances and Applications, vol. 106. Birkhauser, Basel (1998)
Kato T.: Perturbation Theory of Linear Operators. Springer, Berlin (1966)
Kats I.S.: Spectral multiplicity of a second-order differential operator and expansion in eigenfunction. Izv. Akad. Nauk SSSR Ser. Mat. 27(5), 1081–1112 (1963)
Kats I.S.: Linear relations generated by the canonical differential equation of phase dimension 2, and eigenfunction expansion. St. Petersb. Math. J. 14, 429–452 (2003)
Kac, I.S., Krein, M.G.: On spectral functions of a string. In: Supplement to the Russian edition of F.V. Atkinson. Discrete and Continuous Boundary Problems. Mir, Moscow (1968)
Khol’kin A.M.: Description of selfadjoint extensions of differential operators of an arbitrary order on the infinite interval in the absolutely indefinite case. Teor. Funkcii Funkcional. Anal. Prilozhen. 44, 112–122 (1985)
Khrabustovsky V.I.: On the characteristic operators and projections and on the solutions of Weyl type of dissipative and accumulative operator systems. 3. Separated boundary conditions. J. Math. Phys. Anal. Geom. 2(4), 449–473 (2006)
Kogan V.I., Rofe-Beketov F.S.: On square-integrable solutions of symmetric systems of differential equations of arbitrary order. Proc. R. Soc. Edinb. Sect. A 74, 5–40 (1974/75)
Krall A.M.: \({M(\lambda)}\)-theory for singular Hamiltonian systems with one singular endpoint. SIAM J. Math. Anal. 20, 664–700 (1989)
Krishna Kumar V.: On the Titchmarsh–Weyl theory of ordinary symmetric odd-order differential expressions and a direct convergence theorem. Quaest. Math. 5, 165–185 (1982)
Langer H., Textorious B.: On generalized resolvents and Q-functions of symmetric linear relations (subspaces) in Hilbert space. Pac. J. Math. 72(1), 135–165 (1977)
Lesch M., Malamud M.M.: On the deficiency indices and self-adjointness of symmetric Hamiltonian systems. J. Differ. Equ. 189, 556–615 (2003)
Malamud M.M.: On the formula of generalized resolvents of a nondensely defined Hermitian operator. Ukr. Math. Zh. 44(12), 1658–1688 (1992)
Malamud M.M., Mogilevskii V.I.: Krein type formula for canonical resolvents of dual pairs of linear relations. Methods Funct. Anal. Topol. 8(4), 72–100 (2002)
Mogilevskii V.I.: Nevanlinna type families of linear relations and the dilation theorem. Methods Funct. Anal. Topol. 12(1), 38–56 (2006)
Mogilevskii V.I.: Boundary triplets and Krein type resolvent formula for symmetric operators with unequal defect numbers. Methods Funct. Anal. Topol. 12(3), 258–280 (2006)
Mogilevskii V.I.: Description of spectral functions of differential operators with arbitrary deficiency indices. Math. Notes 81(4), 553–559 (2007)
Mogilevskii V.I.: Boundary pairs and boundary conditions for general (not necessarily definite) first-order symmetric systems with arbitrary deficiency indices. Math. Nachr. 285(14–15), 1895–1931 (2012)
Mogilevskii V.I.: On exit space extensions of symmetric operators with applications to first order symmetric systems. Methods Funct. Anal. Topol. 19(3), 268–292 (2013)
Orcutt, B.C.: Canonical differential equations. Dissertation, University of Virginia (1969)
S̆traus A.V.: On generalized resolvents and spectral functions of differential operators of an even order. Izv. Akad. Nauk. SSSR, Ser. Mat. 21, 785–808 (1957)
Weidmann J.: Spectral theory of ordinary differential operators. In: Lecture Notes in Mathematics, vol. 1258. Springer, Berlin (1987)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mogilevskii, V. On Eigenfunction Expansions of First-Order Symmetric Systems and Ordinary Differential Operators of an Odd Order. Integr. Equ. Oper. Theory 82, 301–337 (2015). https://doi.org/10.1007/s00020-015-2224-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00020-015-2224-7