Hellenic Vestiges in the Bastioned Front of the Late 1700s

Abstract

Carlo Borgo’s treatise on military architecture, Analisi ed esame ragionato delle fortificazioni e difesa delle piazze was published in 1777. What astonishing novelty must have struck the king of Prussia, Federico II of Hohenzollern, to whom the author had dedicated the book, to inspire him to commission the author, a simple cleric who by culture was far removed from the violent world of warfare, as “Honorary Lieutenant Colonel of Engineering”? One of the many possible answers might be that the scholarly Jesuit, a lover of the classics, in reading some Hellenic treatises, noted fortification criteria that could be used for the design of a revolutionary bastioned front, one more suited to the interdiction fire of individual weapons and thus less onerous and more effective.

Introduction

Carlo Borgo (Vicenza 1731—Parma 1794) was a teacher of literature in the schools of the Society of Jesus of which he was member, and later of theology at the University of Modena (Pignatelli 1971; Olivier-Poli 1824; Alfieri and Amorth 1992). He is the author of a treatise on military architecture entitled Analisi ed esame ragionato delle fortificazioni e difesa delle piazze (Borgo 1777). The erudite prelate’s interest in this particular discipline is already surprising, but even so is the high regard in which he was held by Frederick II, King of Prussia, one of the greatest reformers of the military institution of the era (Carsten 1954), who made Borgo an honorary Lieutenant Colonel of Engineering. However, as we will see, this is only an apparent paradox.

The treatise met with great public success, confirmed by future editions in Spanish (Casseda 2014) and French (Rossignol 1805), but it also aroused the obvious hostility of the Vatican: the pen of the insightful preacher was not spared the criticism of the Pontiff, Clement XIV, signatory of the 1773 edict Dominus ac Redemptor, abolishing the order founded by Ignatius of Loyola.¹ This was sufficient reason for the Curia to fear that Borgo’s work might in some manner become doctrine for the exiled members of the order (Guasti 2006), as was the dedication to Frederick II, a renowned military expert who protected and welcomed to his kingdom members of the deprecated Society of Jesus, and certainly not for mere theological reasons!

Nevertheless, Borgo clearly stated that the treatise, apart from any real or alleged controversy, was intended to complete the work of Sébastien Le Prestre, Marquis de Vauban, the Marshall of France who in the preceding century had constructed over a hundred strongholds, and taken as many more, using the successful tactic of obsidional attack.²

Of the 300 pages of his treatise, about thirty—the most interesting for us—propose original concepts that, according to the author, are “so novel that I am honoured to have discovered such vast realms where modern intellects may enter and take with them new and great inventions” (Borgo 1777: 239). There are also many explanatory Tavole (plates) and illustrations of the principles, “all fundamental”, in the first four books and in the Appendix to Book IV. Of these, Tav. XI, XII, XIII, XVI and XVII appear to confirm the consistent use of geometric criteria as the basis for flanking tactics.

The Design of the Geometric Configuration as Basis for the Defence Plan

Every section of the ground must be reachable from at least two directions, so that the firing trajectories may intersect before the walls. Such is the guiding principle of the bastioned front which resulted, for perimeter fortifications intended to protect the town, in a closed and wedge-shaped perimeter: acute angles that assured the absence of any concealed sectors and blind spots, called “salient” if directed outward and “recessed” if directed inward. As a necessary corollary to decrease the vulnerability of masonry walls, they lowered—both in an absolute sense by decreasing their height, and in a relative sense by sinking them further into the ground—a number of additional structures, beyond the ditches, which completed and complicated defence. Thus it was that by the beginning of the nineteenth century, “guards”, “lunettes” and “tenailles” often ended up making the urban fortification larger than the town it was intended to protect! This paradox had certainly not gone unnoticed half a century prior, when Carlo Borgo designed a stronghold, envisioning it as embedded within the bend of a river 300 toise wide (the toise was the unit of measure used in France at the time, equivalent to about 6 feet, or 1.949 m):

Diasi prima un’occhiata al corpo intero della mia Piazza. Io l’ho posta alle sponde d’un gran fiume largo 300 tese senza l’imbarazzo, o l’aiuto d’isole, o secche, o paduli. Due gran lati d’oltre 1000 tese ciascuno appogiansi al fiume; dove convergono, lasciano tra i loro capi luogo alla Cittadella di circa 1000 tese anch’essa in lunghezza, per cui la strettezza delle costruente nostre maggiore viene compensata (Borgo 1777: 240–250).

(I first take a look at the entire body of my Square. I have located it on the banks of a large river 300 toises wide unhindered, and unaided, by islands, dry places or marshes. Two long sides over 1,000 toises each flank the river; where these converge, they leave between their ends a space for the Citadel, this too about 1,000 toises long, so that the narrowness of our largest construction is compensated) (Fig. 1).

Fig. 1

Borgo’s design of a stronghold next to a river (1777: Tav. XIII)

The author views fortified fronts as “extremely new”, and so they appear even today if we compare then with the features of the “modern style”, or “star fortress”, which are basically variations on the guiding principle that was followed starting with the construction of the fortress of Neptune in 1501, a fortress with a square layout, and small rounded ramparts. Although we cannot consider Antonio da Sangallo the Elder (1445–1534), to whom the design is attributed, as the inventor of the pentagon shaped bastion, he must certainly be considered as the specialist who taught military engineers how to structure the bastion symmetrically around a bisecting axis in order to better protect the curtain wall from raking and cross fire. To this end, a few years later, the bastions were augmented by “traitor” embrasures, so-called because they were concealed behind the protrusions of the bastion’s facade (orecchioni if rounded, musoni if square), succeeding, in this manner, in eliminating attackers by sweeping all areas with raking artillery fire.

Borgo makes use of orillons, embrasures, counter bastions and actual bastions to analyze obsidional defence (Fig. 2).

Fig. 2

Measurements and solidity of the semicircular fortification module, and nomenclature of the bastion. Image: Halyna Karmazyn

After explaining the nomenclature used, he goes on to describe its features, accurately specifying measurements. Again taking the toise as the unit of measurement, the planimetry of the whole provides us with the dimension and characteristics of the three defensive fronts, extending over approximately 585 m.

This leads to various considerations, but what we wish to emphasise here is the module, easily repeatable, semicircular in shape and with an outward facing concavity located between two reinforced and protruding sides. The axis is the linea capitale, capital line, forming an interaxis of 120 toises between the semi circumferences and thus a modular distance of 248 m, just slightly less than the effective range of raking artillery or other guns of the era. After explaining what he means by long and short bastion, he indicates the median points of every front (curtain wall) compared to the linea magistrale, magistral line, corresponding to the orthogonal of the diameter, upon which intersect the “lines of defence”, the ideal extensions of the acute angles that delineate the reinforced and protruding apexes³ (Fig. 3).

Fig. 3

Detail of the rectilinear section of the citadel (Borgo 1777: Tav. XII)

It is immediately apparent that his intent is to lessen the negligible reactivity of the bastion as he is perfectly aware that this certainly provides for a significant passive defence, greater resistance to fire and an effective protection of the walls, but it does not provide for an equally effective active defence. Borgo writes:

La nostra fortificazione moderna non è di sua natura suscettibile di un sistema di difesa in cui il Cannone abbia la prima parte. La cosa è di così somma importanza che nulla mi conviene di ommettere per ben dichiararla … Il sistema comune delle nostre Piazze moderne non è capace di sua natura di una assai forte difesa di Cannone (Borgo 1777: 198–199).

(Our modern fortification is not by its nature susceptible to a system of defence in which the Cannon plays the primary role. This is of such extreme importance that it is in no way opportune for me to omit declaring this explicitly. …The common system of our modern strongholds is not by its nature capable of providing a strong defence against cannons.)

On the other hand, the volume of fire issuing from muskets held by hundreds of men, was certainly superior both in stopping the enemy and in cost effectiveness compared to cannons. In fact, the winding nature of the enclosures, in addition to protecting the besieged from flank fire, allowed them to multiply the number of gun ports for muskets, saturating the ground in front with multiple trajectories. In addition, the facades of the bastions, which were normally quite extensive, could be more contained, perhaps barely 20 toises long (circa 39 m.) and the communication trenches connecting the different heights of every advanced bastion to a counter-bastion safer and faster (Fara 1989: 250) (Fig. 4).

Fig. 4

Spirit of the layout: use of and reasons of the bastion. Image: Halyna Karmazyn

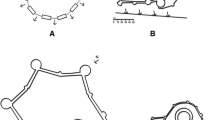
The idea, new compared to the repeated use of the star fort model, reprises a concept based on the premises of several, non-conventional, Hellenic walls, such as the rectilinear surrounding walls that were not obliged to conform to geographical characteristics. These included the zigzag layout and the turreted wall found in sections of the fourth-century city walls of Mileto, Priene, Dura Europos, Apollonia and Siracusa, to cite just a few of the best known (Figs. 5, 6, 7, 8, 9) and that later evolved into the Mesopirgo walls of the Roman era, parts of which are still present in the perimeter ruins of Herculea Telesina (modern-day Benevento, Italy) (Quilici 1966; Russo 1991).

Fig. 5

Planimetry of Mileto: the southern sections of the zig-zag wall. Image: author

Fig. 6

Priene: the walls along the southern sections are in rectangular triangle sawtooth pattern. Image: author

Fig. 7

Planimetry of Dura Europos, with some sections of the city walls in zig-zag pattern. Image: author

Fig. 8

Planimetry of Apollonia: the sawtooth wall in rectangular triangle, reinforced by the inclusion of a tower. Image: author

Fig. 9

Syracuse structure in isosceles triangle saw-tooth pattern satellite view of the insertion of sawtooth curtain walls in Castello Eurialo. Image: author

Even then it was obvious that if the arrows launched from the avant-corps jutting out from the curtain wall near gateways, which will later develop into towers, had a lethal impact for about a hundred meters if they were directed low and horizontally, and that even if they were hurled haphazardly could strike anyone along their trajectory. Further, if the trajectory were parallel to the walls (enfilade) it would bring down many of the attackers (flank fire). Thus, according to Vitruvius, whom we know relied on Greek sources:

The distances between towers are to be set so that they are no further than a bowshot apart, so that if any of the towers is attacked, the enemy could be driven back by scorpiones and other projectile-throwing machines fired from the towers located at right and left [Vitruvius, Book I, Ch. V (2009: 25)] (Fig. 10).

Fig. 10

Graphic reconstruction of a segment the concave segment of the curtain wall with hexagonal towers axonometry of the Herculea Telesina (Benevento, Italia) wall. Image: Halyna Karmazyn

It does not surprise us therefore that a lover of the classics, knowledgeable of Greek and Latin, might have studied the Art of the Siege, the only treatise that has come down to us, albeit only in sections, by Aeneas the Tactician who lived in the fourth century B.C., or the better known Paraskeuastica (παρασκευαστικά) (ca 280/220 B.C.), Book V of the ΜηχανικήΣύνταξις (Treatise on Mechanics) by Philo of Byzantium (Garlan 1974). A probable result of his monastic studies may have been his interest in geometric logic and mathematical calculations, as well as the technology of the classical era in general. Confirmation of this assertion is his drawing of an optical field telegraph (Fig. 88) in Plate XI of the Treatise (Fig. 11), an obvious re-elaboration of the archetype envisioned by Aeneas in his Art of the Siege.⁴

Fig. 11

Borgo’s optical telegraph and construction of the front of the citadel (Borgo 1777: tav. XI, Figs. 87, 88]

But the most significant feature of the Hellenic evocations found in Borgo’s eighteenth-century treatise, is an aspect ascribed to the abstract logic underlying the turreted walls described by Philo. The author of the Treatise on Mechanics suggested polygonal towers, with the angle directed outward (exactly like the bastions that will be built 1,500 years later) in order to eliminate blind spots and thus protect the walls “even if attacked by siege machines” (Garlan 1974: 291, liberal translation).

In studying the preventive potential of cross fire, Philo considers the various advantages offered by semi-circular walls:

There is another system of fortification not at all inferior to previous ones, consisting of semicircles placed in such a manner their concave parts face the enemy. With this system the extremities of the arches must be inserted into the towers, bonding with their angles and enclosing them, starting from the extrados of the circumference and for a width equal to that of the interior wall of the cyma of the towers (Garlan 1974: 296, liberal translation).

Such archetypes have been found in Spain, near Pajares. In an area of 14 hectares are ruins of circular towers all along the perimeter, each sufficiently close to allow maximum range to the arrows released by bows and rudimentary crossbows. Similar ones have also been found along the valley of the middle course of the Guadalquivir, including the concave curtain walls of Camorra (Moret 1966: 120).

The advantages implicit in having curved sections of the wall did not escape even the astute Niccolò Machiavelli (1469–1527), who did not neglect to point out, in spite of the prevailing model of star fort, that in order to prevent the ditches from filling with the debris of walls collapsing under artillery fire, they had to make the ditch wider and deeper and, at the same time, give the curtain wall a winding direction and concavity, features ideal for flank manoeuvres:

Se il nimico ti viene a scalare, l’altezza del primo muro facilmente ti difende. Se viene con l’artiglierie, gli conviene prima battere il muro primo; ma battuto ch’egli è, perché la natura di tutte le batterie è fare cadere il muro di verso la parte battuta, viene la rovina del muro, non trovando fosso che la riceva e nasconda, a raddoppiare la profondità del fosso; in modo che passare più innanzi non ti è possibile, per trovare una rovina che ti ritiene, uno fosso che ti impedisce e l’artiglierie nimiche che dal muro del fosso sicuramente ti ammazzano. Solo vi è questo rimedio: riempiere il fosso; il che è difficilissimo, sì perché la capacità sua è grande, sì per la difficultà che è nello accostarvisi, essendo le mura sinuose e concave; tra le quali, per le ragioni dette, con difficultà si può entrare, e di poi avendo a salire con la materia su per una rovina che ti dà difficultà grandissima; tanto che io fo una città così ordinata al tutto inespugnabile (Machiavelli 1971: Bk. VII, 162).

(If the enemy comes to scale your wall, the height of the first wall easily protects you. If he comes with artillery, he must first batter down the first wall: but once it is battered down, because the nature of all batterings is to cause the wall to fall toward the battered side, the ruin of the wall will result (since it does not find a ditch which receives and hides it) in doubling the depth of the ditch, so that it is not possible for you to pass on further as you will find a ruin that holds you back and a ditch which will impede you, and from the wall of the ditch, in safety, the enemy artillery kills you. The only remedy there exists for you, is to fill up the ditch: which is very difficult, as much because its capacity is large, as from the difficulty you have in approaching it, since the walls being winding and recessed, you can enter among them only with difficulty (Machiavelli 2003: Bk. VII, 125).

On the Shape of the Front and Its Relations with Modern Mathematics

What appears to distinguish Borgo’s defensive layout from others is therefore its intrinsic geometric concept, a concept that allows for calculation of each component, in accordance with the Enlightenment culture of the eighteenth century. The problems he studied in the design and its elevation can, in fact, all be calculated according to the angle formed by the bastions and the trajectories of the projectiles. In order to assess the validity of his idea, the scholarly Jesuit envisions a plan of attack (Fig. 12).

Fig. 12

“Spirit of the layout”: use of and explanations of its sections (Borgo 1777: Tav. XVII)

After reiterating his reasons for disregarding defensive manoeuvres in front of the walls to focus on defending the walls themselves (Borgo 1777: 257–260), he describes the outline of the structure, starting with the principal line, which he designates as WW′ (see Borgo’s Fig. 87, Tav. XI in our Fig. 11), and the lack of any obstructions between the two terreplains (upper and lower), the ditch filled with water and the tenaille (Figs. 13, 14):

Fig. 13

Features of the plan viewed in transversal and longitudinal sections. Image: Halyna Karmazyn

Fig. 14

Axonometric sections of semicircular walls as proposed by Carlo Borgo. Image: Halyna Karmazyn

Ho supposto il livello dell’ acqua 2 tese al dissotto del livello della campagna …La Tanaglia si leva sopra il livello dell’acqua 2 tese, perche la sua piazza resti 6 piedi piu alta di cotesto livello …Il Ramparo basso si leva 3 tese sopra la piazza della Tanaglia: non si poteva alzarlo meno perche il fuoco del Ramparo non incomodasse i Difensori della Tanaglia. …Il Ramparo alto sollevasi 4 tese sopra la Piazza del Ramparo basso; e cio per le ragioni ora dette, ed inoltre perche il suo dominio sullo spalto sia piu forte, ed esteso. La cresta dello spalto giunge al livello orizzontale del Ramparo basso, volendosi assolutamente, che tutto questo Ramparo basso sia intatto ad accogliere il nemico giunto sulla contrascarpa. …dunque 2 tese pure sopra la campagna si leverà la cresta dello spalto, il cui declivie prendendosi dalla sommita del Ramparo alto (Borgo 1777: 249–250).

(I have supposed the level of water to be 2 toises underneath the ground… The Tenaille is 2 toises above the water level, so that the stronghold is 6 feet higher than this level [the ground level]; …The lower Rampart [or glacis] rises 3 toises above the piazza of the Tenaille: it cannot be raised less than this because the fire of the Rampart will strike the defenders. …The upper Rampart rises 4 toise above the piazza of the lower Rampart; this for reasons already mentioned and in order to ensure that its command over the earthwork is greater and more extensive. The top of the earthwork will arrive at the horizontal level of the lower Rampart, to ensure that the lower Rampart remains intact in order to receive the enemy coming from the counterscarp. …. Thus the top of the earthwork rises 2 toise above the ground, whose slope is to be calculated by taking it from the top of the upper rampart.)

Considering that any perimeter fortification must surround the town or military fortress, Borgo focuses on what he defines as “the lateral ends of the citadel”. Here the module, at first thought to be infinitely repeatable, must of necessity end by surrounding the town (see Borgo’s Fig. 88, in our Fig. 11), thus the axes of the angles must no longer be parallel and must converge inward. He writes:

Le cose dette finora suppongono una lunghezza indefinita, e continuata di Fortificazione. La Piazza però disegnata nella Fig. XCII ha delle voltate, e dei termini, che esigono delle variazione nella Construzione. La più grande variazione è nella Cittadella (1777: 254).

(What we have so far stated presupposes an indefinite and continuous length of the Fortification. But the stronghold drawn in Fig. XCII has curves and elements that require a variations in the construction. The most significant variation is in the Citadel.)

He thus invites the Reader to make a “meticulous comparison”, explaining how nella metà di un Ottangolo una strana specie io presento di Fortificazione circolare (in the middle of the Octagon, I submit a strange type of circular fortification) (1777: 198). The geometric logic implicit in the configuration of Fig. 104, Tav. XVI (Fig. 15), is not very different, when he replaced the eight peaks with five, forming a closed catenary.⁵

Fig. 15

Layout for a pentagonal stronghold (Borgo 1777: Tav. XVI, Fig. 104)

By adapting to the morphology of an ideal model (Sardi 1639), thus one that is geometrically regular, both geometric variations may be conducible to the abstraction of a single mathematical problem whose rectilinear development is its extreme example. In the latter, the linee capitali (capital lines, or axes of the bastions) follow each other in a parallel manner, always forming 90° angles to a horizontal point of reference, as they are all orthogonal to the alignment of the diameter of each semi-circle. In order to achieve a closed form, on the other hand, the capital lines must converge toward a centre. In order for the semicircles not to intersect, the distance between the respective centres may never exceed twice the range, which means that, with respect to the horizontal reference, they cannot exceed 45° internally, an exceptional condition corresponding to the octagonal figure, and not coincidentally Borgo’s initial proposal (Figs. 16, 17).

Fig. 16

Construction of the front of the citadel: study of octagonal configuration. Image: Halyna Karmazyn

Fig. 17

Construction of the front of the citadel: study of hexagonal configuration. Image: Halyna Karmazyn

Conclusions

The redesigning of geometric criteria, that is, the principles of calculation that characterise the description of the obsidional defence plan proposed by Borgo, induces one to consider every aspect of Hellenic as well as Renaissance fortification culture as theoretically acceptable. The criteria used to configure the angles and directions in Hellenic fortifications, taking into account the changed masses and ranges of the projectiles launched first by ballistae and later by cannons, remain unchanged, while regarding those of the Renaissance, mathematical calculations are required to contain costs and optimize active and passive defence. This is a capacity in which Borgo shows himself to be a great master, thus justifying his fame as a valid mathematician and scientific scholar among his peers.

In this perspective, the “extremely novel” defence plan discussed in Analisi ed esame ragionato delle fortificazioni, becomes the end point of a speculation that, coming to us from afar, has now reached its apex.⁶ The breech-loading rifle cannons invented by General Cavalli that fired cylinder-ogival projectiles, modified their trajectories by gyroscopic effect, becoming highly ordinate and strongly parabolic (Russo 1999). By striking targets behind walls, the system that had remained unaltered for two centuries since the introduction of firearms, proved to be at least highly inadequate, if not wholly obsolete. Consequently, the Hellenic criteria that, albeit with periodic updates and adaptations to different types of firearms, had remained a tactical invariance, declined irreversibly. But until then, those criteria so ably updated by Borgo, reducing ground movements and the amount of artillery needed for their defence, with significant reduction of costs and times, explains the great honours paid to him by Frederick II of Prussia.