Cycle-time and residence-time density approximations in a stochastic model for circulatory transport

Abstract

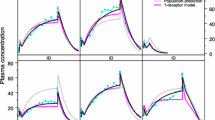
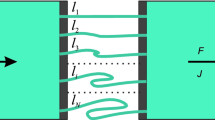
The concentration of a drug in the circulatory system is studied under two different elimination strategies. The first strategy—geometric elimination—is the classical one which assumes a constant elimination rate per cycle. The second strategy—Poisson elimination—assumes that the elimination rate changes during the process of elimination. The problem studied here is to find a relationship between the residence-time distribution and the cycle-time distribution for a given rule of elimination. While the presented model gives this relationship in terms of Laplace-Stieltjes transform, the aim here is to determine the shapes of the corresponding probability density functions. From experimental data, we expect positively skewed, gamma-like distributions for the residence time of the drug in the body. Also, as some elimination parameter in the model approaches a limit, the exponential distribution often arises. Therefore, we use laguerre series expansions, which yield a parsimonious approximation of positively skewed probability densities that are close to a gamma distribution. The coefficients in the expansion are determined by the central moments, which can be obtained from experimental data or as a consequence of theoretical assumptions. The examples presented show that gamma-like densities arise for a diverse set of cycle-time distributions and under both elimination rules.