Abstract
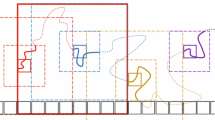
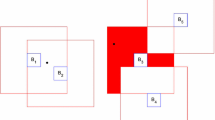
Let ψ(x),x∈ℝ2, be a random field, which may be viewed as the potential of an incompressible flow for which the trajectories follow the level lines of ψ. Percolation methods are used to analyze the sizes of the connected components of level sets {x:ψ(x)=h} and sets {x:ψ(x)≦h} in several classes of random fields with lattice symmetry. In typical cases there is a sharp transition at a critical value ofh from exponential boundedness for such components to the existence of an unbounded component. In some examples, however, there is a nondegenerate interval of values ofh where components are bounded but not exponentially so, and in other cases each level set may be a single infinite line which visits every region of the lattice.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. V. Gruzinov, M. B. Isichenko, and Ya. L. Kalda, Two-dimensional turbulent diffusion,Zh. Eksp. Teor. Fiz. 97:476–488 (1990) [Sov. Phys. JETP 70:263–269 (1990)].
M. B. Isichenko, Percolation, statistical topography, and transport in random media,Rev. Mod. Phys. 64:961–1043 (1992).
M. B. Isichenko, Ya. L. Kalda, E. B. Tatarinova, O. V. Tel'kovskaya, and V. V. Yan'kov, Diffusion in a medium with vortex flow,Zh. Eksp. Teor. Fiz. 96:913–925 (1989) [Sov. Phys. JETP 69:517–524 (1989)].
S. A. Trugman and S. Doniach, Vortex dynamics in inhomogeneous superconducting films,Phys. Rev. B 26:3682–3697 (1982).
A. Weinrib, Percolation threshold of a two-dimensional continuum system.Phys. Rev. B 26:1352–1361 (1982).
A. Weinrib and B. I. Halperin, Distribution of maxima, minima, and saddle points of the intensity of laser speckle patterns,Phys. Rev. B 26:1362–1368 (1982).
J. M. Ziman, The localization of electrons in ordered and disordered systems, I. Percolation of classical particles,J. Phys. C 1:1532–1538 (1968).
M. Avellaneda, F. Elliot, Jr., and C. Apelian, Trapping, percolation and anomalous diffusion of particles in a two-dimensional random flow,J. Stat. Phys. 72:1227–1304 (1993).
S. A. Molchanov and A. K. Stepanov, Percolation in random fields I, II, III,Teor. Mat. Fiz. 55:246–256, 419–430;67:177–185 (1983) [Theor. Math. Phys. 55:478–484, 592–599;67:434–439 (1983)].
G. Grimmett,Percolation (Springer-Verlag, New York, 1989).
H. Kesten,Percolation Theory for Mathematicians (Birkhäuser, Boston, 1982).
L. Russo, On the critical percolation probabilities,Z. Wahrsch. Verw. Gebiete 56:229–237 (1981).
Y. Higuchi, Coexistence of the infinite (*) clusters: A remark on the square lattice site percolation,Z. Wahrsch. Verw. Gebiete 61:75–81 (1982).
M. Aizenmann and D. J. Barsky, Sharpness of the phase transition in percolation models,Commun. Math. Phys. 108:489–526 (1987).
J. M. Hammersley, Percolation processes. Lower bounds for the critical probability,Ann. Math. Stat. 28:790–795 (1957).
M. V. Men'shikov, S. A. Molchanov, and A. F. Sidorenko, Percolation theory and some applications,Itogi Nauki Tekhniki (Ser. Prob. Theory Math. Stat. Theoret. Cybernet.) 24:53–110 (1986) [J. Sov. Math. 42:1766–1810 (1988)].
M. Aizenman and G. Grimmett, Strict monotonicity for critical points in percolation and ferromagnetic models,J. Stat. Phys. 63:817–835 (1991).
K. S. Alexander, Percolation and minimal spanning forests in infinite graphs,Ann. Prob. (1994), to appear.
F. P. Preparata and M. I. Shamos,Computational Geometry: An Introduction (Springer-Verlag, New York, 1985).
D. Aldous and J. M. Steele, Asymptotics for Euclidean minimal spanning trees on random points,Prob. Theory Rel. Fields 92:247–258 (1992).
R. Pemantle, Choosing a spanning tree for the integer lattice uniformly,Ann. Prob. 19:1559–1574 (1991).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Alexander, K.S., Molchanov, S.A. Percolation of level sets for two-dimensional random fields with lattice symmetry. J Stat Phys 77, 627–643 (1994). https://doi.org/10.1007/BF02179453
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02179453