Skip to main content
SpringerLink
Log in

Homoclinic orbits and mixed-mode oscillations in far-from-equilibrium systems

  • Articles
  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

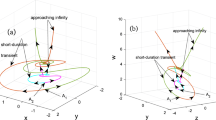
Nonlinear autonomous dynamical systems with ahomoclinic tangency to a periodic orbit are investigated. We study the bifurcation sequences of the mixed-mode oscillations generated by the homoclinicity, which are shown to belong to two different types, depending on the nature of the Liapunov numbers of the basic periodic orbit. A detailed numerical analysis is carried out to show how the existence of a tangent homoclinic orbit allows us to understand in a quantitative way a particular and regular sequence of cool flame-ignition oscillations observed in a thermokinetic model of hydrocarbon oxidation. Chaotic cool flame oscillations are also observed in the same model. When the control parameter crosses a critical value, this chaotic set of trajectories becomes globally unstable and forms a Cantor-like hyperbolic repellor, and the ignition mechanism generates ahomoclinic tangency to the Cantor set of trajectories. The complex bifurcation diagram may be globally reconstructed from a one-dimensional dynamical system, thanks to the strong contractivity of thermokinetics. It is found that a symbolic dynamics with three symbols is necessary to classify the periodic windows of the complex bifurcation sequence observed numerically in this system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J.-C. Roux,Physica 7D:57 (1983), and references therein.

    Google Scholar 

  2. J. S. Turner, J.-C. Roux, W. D. McCormick, and H. L. Swinney,Phys. Lett. 85A:9 (1981).

    Google Scholar 

  3. C. Vidal, Dynamic instabilities observed in the Belousov-Zhabotinsky system, inChaos and Order in Nature, H. Haken, ed. (Springer, Berlin, 1981), pp. 69–82.

    Google Scholar 

  4. J. L. Hudson, M. Hart, and D. Marinko,J. Chem. Phys. 71:1601 (1979).

    Google Scholar 

  5. M. Orban and I. R. Epstein,J. Phys. Chem. 86:3907 (1982).

    Google Scholar 

  6. P. Gray, J. F. Griffiths, S. M. Hasko, and P. G. Lignola,Combustion Flame 43:175 (1981);Proc. R. Soc. Lond. A 374:313 (1981).

    Google Scholar 

  7. X.-J. Wang and C. Y. Mou,J. Chem. Phys. 83:4554 (1985).

    Google Scholar 

  8. R. H. Simoyi, A. Wolf, and H. L. Swinney,Phys. Rev. Lett. 49:245 (1982).

    Google Scholar 

  9. A. S. Pikovsky,Phys. Lett. 85A:13 (1981).

    Google Scholar 

  10. R. A. Schmitz, G. T. Renola, and P. C. Garrigan,Ann. N. Y. Acad. Sci. 316:638 (1979).

    Google Scholar 

  11. O. E. Rössler,Z. Naturforsch. 31a:259 (1976).

    Google Scholar 

  12. O. E. Rössler, Chaos, inStructural Stability in Physics, W. Güttinger and H. Eikemeier, eds. (Springer, Berlin, 1979), pp. 290–309.

    Google Scholar 

  13. A. Arnéodo, P. Coullet, and C. Tresser,J. Stat. Phys. 27:171 (1982).

    Google Scholar 

  14. C. Tresser,Ann. Inst. Henri Poincaré Phys. Theor. 40:441 (1984).

    Google Scholar 

  15. P. Gaspard and G. Nicolis,J. Stat. Phys. 31:499 (1983).

    Google Scholar 

  16. P. Glendinning and C. Sparrow,J. Stat. Phys. 35:645 (1984).

    Google Scholar 

  17. P. Gaspard, R. Kapral, and G. Nicolis,J. Stat. Phys. 35:697 (1984).

    Google Scholar 

  18. P. Gaspard, Periodic and nonperiodic dynamical behaviors near homoclinic systems, inFluctuations and Sensitivity in Nonequilibrium Systems, W. Horsthemke and D. K. Kondepudi, eds. (Springer, Berlin, 1984), p. 265.

    Google Scholar 

  19. F. Argoul, A. Arnéodo, and P. Richetti, Experimental evidence of homoclinic chaos in the Belousov-Zhabotinskii reaction,Phys. Lett. 120A:269 (1987).

    Google Scholar 

  20. J. Neimark and L. Shil'nikov,Sov. Math. Dokl. 6:305 (1965); L. Shil'nikov,Sov. Math. Dokl. 6:163 (1965);Mat. Sb. 10:91 (1970).

    Google Scholar 

  21. Y. Pomeau and P. Manneville,Commun. Math. Phys. 74:189 (1980).

    Google Scholar 

  22. N. K. Gavrilov and L. P. Shil'nikov,Mat. SSSR Sb. 17:467 (1972);19:139 (1973).

    Google Scholar 

  23. J. Guckenheimer and P. Holmes,Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Field (Springer, New York, 1983).

    Google Scholar 

  24. S. Smale, Differentiable dynamical systems, inThe Mathematics of Time (Springer, New York, 1980), pp. 1–82.

    Google Scholar 

  25. P. Gaspard,Phys. Lett. 97A:1 (1983).

    Google Scholar 

  26. C. Sparrow,The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors (Springer, New York, 1982), Appendix E.

    Google Scholar 

  27. Ya. G. Sinai and E. B. Vul,J. Stat. Phys. 23:27 (1980).

    Google Scholar 

  28. S. De Gregorio,J. Stat. Phys. 38:947 (1985).

    Google Scholar 

  29. Subroutine D02EBF, NAG Fortran Library, Numerical Algorithms Group, Oxford and Illinois (1983).

  30. M. J. Feigenbaum,J. Stat. Phys. 19:25 (1978);21:669 (1979).

    Google Scholar 

  31. T.-Y. Li and J. A. Yorke,Am. Math. Mon. 82:985 (1975).

    Google Scholar 

  32. P. Gray, J. F. Griffiths, and S. M. Hasko,Proc. R. Soc. Lond. A 396:227 (1984).

    Google Scholar 

  33. S. Newhouse,Topology 12:9 (1974);Publ. Math. IHES 50:101–152 (1979).

    Google Scholar 

  34. C. Robinson,Commun. Math. Phys. 90:433 (1983).

    Google Scholar 

  35. P. Hartman,Ordinary Differential Equations (Wiley, New York, 1964).

    Google Scholar 

  36. S. J. van Strien, On the bifurcation creating horseshoes, inDynamical Systems and Turbulence, D. A. Rand and L. S. Young, eds. (Lecture Notes in Mathematics 898, Springer, Berlin, 1981), pp. 316–351.

    Google Scholar 

  37. P. Holmes and R. F. Williams,Arch. Rat. Mech. Anal. 90:115 (1985).

    Google Scholar 

  38. D. Fournier, H. Kawakami, and C. Mira,C. R. Acad. Sci. Paris I 298(11):253 (1984).

    Google Scholar 

  39. P. J. Holmes,Phys. Lett. 104A:299 (1984).

    Google Scholar 

  40. J. H. Curry and J. R. Johnson,Phys. Lett. 92A:217 (1982).

    Google Scholar 

  41. X.-J. Wang, Homoclinic tangency to a Smale horseshoe, preprint (1987).

Download references

Author information

Authors and Affiliations

  1. Faculté des Sciences, Université Libre de Bruxelles, B-1050, Brussels, Belgium

    P. Gaspard & X. J. Wang

Authors
  1. P. Gaspard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. J. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gaspard, P., Wang, X.J. Homoclinic orbits and mixed-mode oscillations in far-from-equilibrium systems. J Stat Phys 48, 151–199 (1987). https://doi.org/10.1007/BF01010405

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01010405

Key words

Search

Navigation