Introduction

Quadrupole mass filters and guides are integral components in many mass spectrometers. These devices are generally operated with sinusoidal waveforms applied to the electrodes with opposing electrodes electrically connected and each pair receiving an rf potential 180° out of phase from the other. Optionally, a DC potential may be applied between the two rod sets to narrow the range of stable m/z values and create a mass filter. For sinusoidal mass filters, the width of the stable mass window is varied by altering the ratio of the DC to rf potentials. The mass window is then scanned by ramping both the DC and rf potentials simultaneously at a fixed frequency.

Recently, a number of non-sinusoidal quadrupole mass filters have appeared in the literature [1, 2]. These devices operate with digitally produced waveforms with the frequency varied and the rf and DC potentials fixed. A mass filter can also be created by imposing a DC potential between the rods and reducing the width of the mass window by increasing the DC/rf potential ratio. Digitally operated quadrupoles can also create mass windows of variable width by changing the duty cycle, δ, (defined as the fraction of the period when the high state is applied [3]) of one or both electrode pairs without applying a static DC potential between the rods. In either mode of operation, the stable mass window of the digitally operated quadrupole mass filter can be scanned by stepping the frequency of the applied waveforms.

Digital ion guides have shown improved ion handling that enables ion collection and MSn in a single guide [4]. Trapezoidally-driven devices were originally examined by Richards et al. in the 1970s when early digital waveform generators exhibited very limited slew rates [5, 6]. More recently, Shinholt et al. [2] produced a digitally driven mass filter that employed trapezoidal waveforms to mass analyze CsI clusters up to 20,000 Th. These nontraditional waveforms present many exciting performance-enhancing possibilities for quadrupole mass spectrometers, but discovering and exploring their unique capabilities requires the ability to accurately plot their stability diagrams. Matrix methods developed by Pipes [7], Richards et al. [5], and others [8–10] over the past 70 years provide the tools that allow mass spectrometrists to analytically solve the Hill equation at all points in the a,q plane and to precisely map the stability diagram of ions confined in an oscillating quadrupolar field. Matrix methods also permit the calculation of the pseudopotential well depth at each point in the a,q plane [11]. These calculations provide the framework for comparison of various mass filters that can be created with sinusoidal and digital waveforms.

Matrix methods for calculating stability diagrams have been applied to rectangular and sinusoidal waveforms [8–12] but they are not limited to these well-studied driving waveforms; these methods are applicable to any periodic quadrupolar potential. In this paper, the performances of quadrupole mass filters (QMF) driven by several different driving waveform are evaluated.

Methods

The Mathieu equation defines ion motion in a sinusoidally oscillating quadrupole field and allows precise prediction of ion trajectories. It is a special case of the more general Hill equation with only 1 harmonic mode. On the other hand, ion motion in any periodically oscillating quadrupolar field can be precisely calculated with the more general Hill equation. The Mathieu and Hill equations are second order linear differential equations that can be solved by standard methods.

One of the methods of solving the Hill and Mathieu equations is the matrix method first outlined by Pipes [7]. This technique relies on creating a series of 2 × 2 matrices describing ion behavior during a series of constant potential steps that comprise one period of the driving waveform [8–10]. If the velocity and position of an ion is known at the beginning of each constant potential interval, the velocity and position of the ion at the end of each interval can be precisely calculated. These matrices may be multiplied sequentially over any portion of an rf period to define ion motion over that interval. Defining the ion motion over one whole period of the waveform establishes whether ion motion is periodic and stable.

In the case of rectangular waveforms, ion stability may be calculated precisely using only a handful of matrices because the waveform can be exactly defined by a small number of constant potential intervals. Continuous waveforms such as sine waves cannot be exactly defined without using an infinite number of constant potential steps, but satisfactory results may be achieved with as few as 14 steps [9]. The accuracy of waveforms approximated by discrete voltage intervals is determined by the number of time/voltage steps used, with additional time steps improving accuracy at the expense of computation time. As a compromise, non-rectangular waveforms treated in this work were approximated with 128 voltage steps. Figure 1 illustrates the stepped waveforms used in the calculations discussed throughout this paper. The duration of all steps need not be equal if variable duration better approximates the continuous waveform. All of the waveforms discussed in this paper are idealized (without any noise or harmonics), but matrix methods may also be used to treat noisy or distorted driving potentials [13].

Figure 1
figure 1

One period of matrix method compatible representations of driving waveforms; 128 constant potential steps approximate each non-rectangular wave

Full size image

The accuracy of these calculations may be judged by comparing the boundaries of the generated stability diagrams with those in the literature. Calculations using the 128 point sine wave predict that the low mass cut-off will occur at q = 0.908, the same value returned by the Mathieu equation. Shinholt et al. [2] report the apex of the stability diagram of one trapezoidal waveform at (0.670, 0.230) found by SIMION ion trajectory simulations. Matrix calculations using a 128 step approximation illustrated in Figure 1 (green trace) of the same trapezoid places the apex at (0.6747, 0.2370).

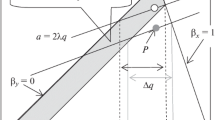
It should be noted that trapezoidal waveforms represent a series of intermediates between rectangular and triangular driving potentials. The stability diagram for trapezoidal waveforms varies dramatically with the slew rate and duty cycle. In the limit where rise time approaches zero, the stability diagram converges on that of a rectangular wave. In the limit where rise time approaches one-half of the period, the stability diagram converges on that of a triangular wave. See Figure 2 for a comparison of stability diagrams for these waveforms. The variation of the trapezoidal stability diagram (green) with slew rate is depicted by the green arrow that lets the apex range between the square wave (blue) and the triangular wave (red) stability diagrams.

Figure 2
figure 2

Stability diagrams for a linear quadrupole using four different driving waveforms. From right: square, trapezoidal, sinusoidal, and triangular. Each unique wave shape generates a unique stability diagram

Full size image

Generating the stability diagram for a particular driving waveform entails calculating the trace of the transfer matrix for a large number of points in the a,q plane. The stable region is bounded by curves where the stability parameter, β, has a value of 0 or 1. At each point within the stable region, β may be calculated from the trace using the following expression for the boundary condition: [3, 8, 10]

$$ \left|\mathrm{T}\mathrm{r}\left({\mathrm{M}}_u\right)\right|={m}_{11}+{m}_{22}=2 \cos \left({\beta}_u\pi \right) $$
(1)

β and various approximations thereof have long been used to calculate the pseudopotential well depth. The canonical relationship between well depth and β is [11]:

$$ {D}_u=-\frac{{\beta_u}^2V}{2{q}_u} $$
(2)

Because the matrix method calculates β as a function of the Mathieu parameters and waveform shape, it is possible to calculate the pseudopotential well depth for a particular driving wave at any point within the stability region. Solving Equation (1) for β and substituting the result into Equation (2) yields an exact expression for the relationship between a, q, and β for any periodic driving waveform [11]:

$$ {D}_u=-\frac{V}{\pi^2{q}_u}{\left[co{s}^{-1}\left(\frac{\left|{m}_{11}+{m}_{22}\right|}{2}\right)\right]}^2 $$
(3)

In this way, independent plots of well depth along the x- and y-axes may be generated over the a,q plane for an arbitrary driving waveform. The well depth plots in Figure 3 were created by comparing the well depth along the guide’s two orthogonal axes and plotting the smaller of the two values. These plots reveal a notable relationship between digital and sinusoidal QMFs. Each point in the digitally driven QMF well depth plot in Figure 3c may be converted to the sinusoidally driven QMF well depth plot (Figure 3a) by scaling the q axis and the value of q in Equation (3) by a factor of 4/π [14]. As a consequence of Equation (2), the well depth of a sinusoidal QMF is shallower by the same factor when the two devices are operated at the same voltage. This numerical relationship between the stability diagrams is not surprising because 4/π is the coefficient of the Fourier series representation of a square wave. There is no substantive difference between a scaled square wave well depth plot and one created by applying methods to an approximated sine wave. Previous work by our group has used two-dimensional well depth plots along the a = 0 line to predict improved performance in digital ion traps by manipulating duty cycle [11]. The three-dimensional plots presented here permit the comparison of quadrupole mass filters operating in different modes and driven by arbitrary rf potentials.

Figure 3
figure 3

Normalized well depth plots of (a) and (b) sinusoidal QMF; (c) and (d) digital QMF with 50/0/50 duty cycle; (e) and (f) digital QMF driven by 61.124/0/38.876 waveform. Ion motion is unstable outside of the red boundary. The figures at right are the enlarged apices of the stability diagrams at left. For each diagram, the cyan line is the a/q ratio required for R = q/Δq = 100

Full size image

Mass Filter Operation

Quadrupole mass filters may be operated in two modes as illustrated in Figure 3. A DC potential may be superimposed on the rf waveform or the duty cycle of the driving waveform may be adjusted. Digital and trapezoidal QMFs may operate in either mode whereas sinusoidal QMFs are limited to the first mode. When a DC potential is used, the a/q scan line (cyan lines in Figure 3) tilts toward the apex of the stability diagram to limit the values of m/z passing through the sinusoidal and 50/0/50 duty cycle digital devices as illustrated in Figure 3a and c, respectively. Figure 3b shows the apex of a sinusoidal mass filter and the line a/q = 0.33314 generating 100 resolving power (R = q/Δq). The stability diagram of a digital mass filter operated with a superimposed DC potential is presented in Figure 3c. The line a/q = 0.42746 intercepts the stability diagram near the apex and generates 100 resolving power. Because the two stability diagrams of these two QMFs are related by a factor of 4/π, the a/q ratio required to achieve the same resolving power is related by the same factor. This relationship also results in a maximum well depth 4/π times greater in digital mass filter. Figure 3e illustrates the second operational mode. Modulating the duty cycle to 61.124/0/38.876 shifts the stability diagram downward to place the apex near the line a/q = 0, which generates equal resolving power 100. Because duty cycle-based ion isolation does not required a DC potential, fewer power supplies are needed to achieve the same results. The two operating modes have much in common, but the comparison of the two modes below reveals subtle differences with large impacts on experimental design.

Results and Discussion

The matrix method discussed above makes it possible to predict the behavior of any quadrupole mass filter. The pseudopotential well depth was calculated for each point in a 1000 × 850 grid covering the first stability region of the a,q plane to create the stability diagrams in Figure 3. The well depth along the indicated a/q lines was calculated at higher resolution (20,000 equally spaced points spanning values of q from 0.5 to 1) and plotted in Figure 4. For the purposes of comparison, appropriate values of a/q or duty cycle were selected for each device to achieve a resolving power, R, of 100. The deepest point in the pseudopotential well was used to define q and the full range of stable q values defined Δq.

Figure 4
figure 4

Comparison of well depth for several mass filters operated with 100 resolving power

Full size image

This may be converted to the more familiar m/Δm definition of resolving power using the definition of the Mathieu parameter, q:

$$ q=\frac{4zeV}{m{r}_0^2{\varOmega}^2} $$
(4)

The resulting relationship is:

$$ \frac{q}{\varDelta q}=\frac{m}{\varDelta m} $$
(5)

Because Δq includes ions that pass through the mass filter regardless of transmission efficiency, Δm obtained from Equation (5) will be larger than what might be observed experimentally. Consequently, the resolving power calculated from q/Δq provides a conservative estimate.

The pseudopotential well depth provides a first order approximation of transmission efficiency [15]. The quantitative relationship between these values may be determined by experiment or by more sophisticated modeling, which accounts for device geometry and the fringe fields experienced by ions entering and leaving the mass filter. For the purposes of comparison, this work assumes only that transmission efficiency increases monotonically with well depth, regardless of q. The calculations presented allow evaluation of the performance of mass filters driven by novel waveforms. At the same rf voltage and resolving power, digital guides outperform sinusoidal systems by a factor of 4/π in terms of sensitivity. However, the differing operating modes of these systems warrants further discussion.

Sinusoidally-driven QMFs operate at fixed-frequency and pass ions through a mass window, the width of which is defined by the ratio of a to q. The mass window is scanned by simultaneously ramping the DC and rf voltages along a constant a/q line to obtain a constant resolving power across the mass range as follows from Equation (5) [16]. Because V is increased to select a higher value of m/z, the maximum well depth also increases as described by Equation (2), resulting in improved sensitivity at constant resolving power. In practice, the a/q ratio of sinusoidal instruments is often increased nonlinearly to maintain a constant mass window (Δm) as the rf voltage is increased. As the a/q line moves closer to the apex of the stability diagram, the value of β approaches the boundary condition. The combination of increasing rf voltage and decreasing the difference between β and its value at the boundary maintains a constant maximum well depth via Equation (2) even as the resolving power (m/Δm) increases.

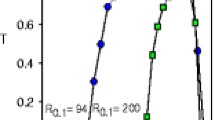
In contrast, digital QMFs operate by varying the frequency and duty cycle of a fixed-magnitude rf wave. As in sinusoidal QMFs, the resolving power of digital quads is constant across a wide range of masses. Because well depth at a given value of q is not affected by frequency, it is mass independent in digital devices. A constant mass window may be maintained with increasing mass for digitally operated quadrupoles by either applying a DC potential between the rod sets or increasing the duty cycle of the driving waveform. However, because the maximum rf voltage remains constant while β approaches the boundary, maintaining a constant mass window with increasing mass concurrently decreases the maximum well depth and sensitivity. The relationship between duty cycle, resolving power, and pseudopotential well depth in a digital QMF may be seen in Figure 5. If there is no non-quadrupolar interval in the driving waveform [3, 17], the well depth reaches 0 V and the resolving power asymptotically increases until a duty cycle of 0.612099. This seems to imply that infinite resolving power is possible. In practice, the resolving power is limited by the presence of buffer gas, imperfections in the electric field, and the ions’ distribution of initial kinetic energies. The symmetry of the ion guide and stability diagram creates another asymptote at 0.387901 which exhibits the same behavior [6].

Figure 5
figure 5

Maximum pseudopotential well depth (circles) and resolving power (triangles) along the a/q = 0 line for digital QMF as a function of duty cycle. Data from matrix calculations are plotted as points. Equations (6) and (7) describe the fitted curves

Full size image

Generating a unique stability diagram for each change in duty cycle may go beyond the needs of the typical digital QMF user. It would be convenient to have an algebraic expression approximating the relationship between duty cycle and resolving power depicted in Figure 5. An empirical fit of the resolving power data yields:

$$ \frac{q}{\varDelta q}=\left(\frac{\delta }{11.5\cdot {\delta}_o\cdot \left|{\delta}_o-\delta \right|}\right) $$
(6)

where δ is the operating duty cycle and δo is the duty cycle at the asymptote. This function tracks q/Δq to within 0.1% for R < 1000 and provides a conservative approximation of operational resolving power. Extremely precise control of duty cycle is required to set a particular Δm because resolving power increases very rapidly as the operating DC approaches δo [6]. This level of duty cycle precision is attainable provided the clock frequency can be phase-coherently switched while the arbitrary wave is being written [18].

Comparing the pseudopotential well depth of two mass filters gives insight into their relative transmission efficiencies. An empirical fit of the maximum well depth obtained at a given duty cycle along the a/q = 0 line is depicted in Figure 5 and may be expressed as:

$$ {D}_{max}=\frac{V_{p-p}}{2}\left(1-\left(\frac{\left|\delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right|}{\delta_o-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right) $$
(7)

The value of q corresponding to the deepest well depth along the a/q = 0 line must be known in order to select the operational parameters for a particular mass. This q value is related to duty cycle in a less straightforward manner than resolving power and well depth, but Equation (8) approximates this relationship with less than 0.2% error. For duty cycles resulting in R > 100, the error drops to less than 0.02%.

$$ {q}_{D_{max}}=0.1085{\left(\frac{\left|\delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right|}{\delta_o-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}^{2.3} $$
(8)

These three equations provide a starting point for designing future experiments utilizing digital quadrupole mass filters.

Conclusion

The relative performances of current and emerging quadrupole mass filter devices were considered. The application of matrix methods to solve the Hill differential equation allows the pseudopotential well depth to be mapped at any point in the a,q plane for arbitrary periodic quadrupolar waveforms. This map was used to examine the relationship between resolving power and sensitivity in sinusoidal and digital quadrupole mass filters. Equations approximating the performance of digital QMF as a function of driving waveform duty cycle were determined.