Study on the Anode-to-Cathode Distance in an Aluminum Reduction Cell

Abstract

A two-dimensional (2D) finite element model (FEM) of an anode immersed in an aluminum reduction cell was developed to study the initial current distribution in the anode as a function of anode geometry and electrical anode conductivity gradients. The numerical results of the initial state of the anode electrical current were used to describe analytically how this will affect the variation in the anode-to-cathode distance (ACD) in a steady-state scenario after several hours in the electrolysis bath. The electrical power loss in the anode has also been studied at different anode geometries and material properties. The slot positioning, slot depths, and stub hole dimensions have been considered in the FEM. The anode is implemented as an inhomogeneous orthotropic material with a defined six-parameter equation. The degree of initial inhomogeneous anode current density, which is expressed with a defined parameter k ₀, can reach values to cause variations in the ACD typically measured in the aluminum industry. To avoid a variation in the ACD for this case, the defined bath conductivity relation n should be within certain limits for the analyzed industrial reduction cell. The lowest degree of initial inhomogeneous current in the anode is achieved with deeper slots closer to each other and with an electrical current entering the anode in the bottom of the anode stub hole.

Introduction

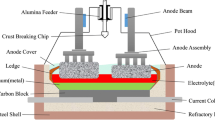
The metal capacity from the aluminum reduction cell increases proportionally with a current increase as long as the current efficiency (CE) is constant. The electrical power loss from the bath resistance as a result of the current increase can be reduced by decreasing the anode-to-cathode distance (ACD). This is preferred to make sure that the pots stay inside an operational resistance load window where sufficient frozen side ledge is retained. When the average of the ACD is reduced by current increase actions, it is important to reduce the variation/noise in the ACD resistance. If not, the process will be directed toward an unstable state with reduced current efficiency and higher probability for dynamic short circuiting, which is caused by magneto hydrodynamic waves and the risk of growing spikes at the anodes wear surface.

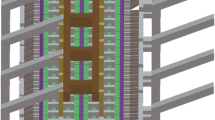
Over the last 10 years, there has been focus on current increase actions and also on reducing the noise in the ACD resistance in the aluminum industry. One of the major improvements of reducing the noise was the implementation of slots in the wear surface as illustrated in Figure 1.[1] The produced carbon dioxide creates bubbles in the bath and the slots function as an escape route for the bubbles. The low-frequency noise components in the liquid metal have also been studied in a magnetohydrodynamic (MHD) aspect that has influenced design optimizations of the cell and also the bus bar system.[2] There is also a focus on how the inhomogeneous density of the bath creates inhomogeneous ACDs.[3] This gives motivation for alumina distribution to the cell through individual feeder control to reduce the density differences in the bath. Still, variations exist in the ACD resistance. In normal situations, it is reported that the standard deviation in the current load on individual anodes in the same cell often are more than 10 pct of the average current.[4] The actions for reducing the noise in the ACD resistance by slots in the anode have led to negative effects on other parameters, like current efficiency and increased inhomogeneous anode consumptions.[5] It is emphasized that each slot implementation must be treated individually for each plant[6] to avoid pitfalls.

Fig. 1

The anode immersed in the electrolysis bath (the longitudinal direction of the anode is into the paper). The slots divide the lower part of the anode into three longitudinal “legs” with height d ₄. Dimension d ₁ is the radius of the stub hole bottom

This article will focus on one special effect on the ACD variation, that is, the initial electric current distribution (the anode in an initial state in the bath as explained previously). The first section of the article defines the k ₀ parameter to describe the degree of initial inhomogeneous current densities in the anode. The parameter is coupled even more by a proposed analytical equation to the ACD to explain how the k ₀ parameter affects the ACD. The anode conductivity gradients are also parameterized with linear and nonlinear parameters by a six-parameter equation to study how different conductivity gradients can affect the ACD through the k ₀ parameter.

In the second part of the article, a two-dimensional (2D) numerical model is developed to determine a typical variation in k ₀ for some realistic anode geometries and anode conductivity gradients. The electric conductivity is implemented in the finite element model (FEM) as an orthotropic inhomogeneous material property with the proposed six-parameter equation. The numerical study of the defined parameter k ₀ is a first study of its kind. We therefore decided to use a 2D model to reduce the complexity and computational burden. The aim was to determine a typical range in the k ₀ parameter and find effects from the anode design that will decrease this parameter. The expected differences in the results from a three-dimensional (3D) FEM compared with a 2D FEM are discussed subsequently in this article.

Parameterization of Inhomogeneous Properties in the Electrolysis Cell

A parameter describing the degree of inhomogeneous electrical current distribution (k ₀) in the anode is defined. It is used in a proposed analytical equation to describe its effect on the variation in the ACD.

The k Parameter

For simplicity, we can introduce a parameter k to describe a relation of ideal electrical current density J ₂ in the inner leg of the anode and a current density J ₃ in the outer leg of the anode as shown in Figure 1. The current density, J ₃ can be taken as an abnormal current density and J ₂ as a reference current density.

For the ideal initial state (k = k ₀), we have

$$ J_{3} = k_{0} J_{2} $$

(1)

Equation [1] can also be expressed with electrical current and cross section as

$$ {\frac{{I_{3} }}{{A_{3} }}} = k_{0} {\frac{{I_{2} }}{{A_{2} }}} $$

(2)

For the ideal steady state, after several hours in the bath, different processes like surface overvoltage on the anode wear surface, production of CO₂, and anode consumption will result in a homogeneously distributed current near the anode wear surface. This means that k→1 and J ₃ = kJ ₂ = J ₂. The initial degree of inhomogeneous current distribution k ₀ has been transferred over to the steady state by Eq. [3]. The resistances for path 2 and path 3 (the paths down to the metal pad in Figure 2) get the relation

$$ A_{3} R_{3} = k_{0} A_{2} R_{2} $$

(3)

Fig. 2

Equivalent DC circuit of an anode in the bath. The current density J is affected by anode resistance R _an, surface overvoltage resistance R _ov, bubble resistance R _bu, and the resistance in the bath R _ba. The left circuit can be simplified to the right DC circuit where $R_{\rm ba}^{\prime}$ is the resistance that includes R _ov, R _bu, and R _ba. The length l ₂ is the height of the anode where J ₂ is dominant. The length l ₃ is the height of the anode where J ₃ is dominant. The length L is the total vertical length from a common reference horizontal plane in the anode down to the metal pad

The equivalent direct current (DC) circuits of the anode in the bath, which are shown in Figure 2, are used to describe how inhomogeneous current density can affect the ACD. The high resistances in the cell and the resistances that are highly affected by the current density are included in the equivalent DC circuit (the Nernst potential, anode concentration overvoltage, and the cathode overvoltage are therefore neglected).

Equation [3] can further be expressed, with components described in Figure 2, as

$$ A_{3} \left( {R_{{{\text{an}}3}} + R_{{{\text{ba}}3}}^{\prime } } \right) = A_{2} k_{0} \left( {R_{{{\text{an}}2}} + R_{{{\text{ba}}2}}^{\prime } } \right) $$

(4)

By expressing the resistances as a function of its conductivities and dimensions $\left( {R = {\raise0.7ex\hbox{$l$} \!\mathord{\left/ {\vphantom {l {\sigma A}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma A}$}}} \right)$ we get

$$ {\frac{{l_{3} }}{{\sigma_{{{\text{an}}3}} }}}\,+\,{\frac{{L - l_{3} }}{{\sigma_{{{\text{ba}}3}}^{\prime } }}} = k_{0}\,{\frac{{l_{2} }}{{\sigma_{{{\text{an}}2}} }}}\,+\,k_{0} \,{\frac{{L - l_{2} }}{{\sigma_{{{\text{ba}}2}}^{\prime } }}} $$

(5)

We assume homogenous conductivity in the anode and introduce the conductivity relations $m = {\raise0.7ex\hbox{${\sigma_{\text{an}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{an}} } {\sigma_{{{\text{ba}}2}}^{\prime } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma_{{{\text{ba}}2}}^{\prime } }$}}$ and $n = {\raise0.7ex\hbox{${\sigma_{{{\text{ba}}3}}^{\prime } }$} \!\mathord{\left/ {\vphantom {{\sigma_{{{\text{ba}}3}}^{\prime } } {\sigma_{{{\text{ba}}2}}^{\prime } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma_{{{\text{ba}}2}}^{\prime } }$}}.$ Equation [5] can then be expressed as

$$ {\frac{{l_{3} }}{m}}\,+\,{\frac{{L - l_{3} }}{n}} = k_{0}\,{\frac{{l_{2} }}{m}}\,+\,k_{0} \left( {L - l_{2} } \right) $$

(6)

By finding an expression for l ₃ from Eq. [6], we get Eq. [7] for the ideal steady state.

$$ l_{3} = {\frac{{k_{0} nl_{2} + k_{0} mn\left( {L - l_{2} } \right) - mL}}{n - m}} $$

(7)

For the case of n = k ₀ = 1, no difference in the ACD, because of the anode design, will appear because l ₃ = l ₂ in Eq. [7] (ACD _ref = L − l ₂ = ACD _abnorm = L − l ₃), and no inhomogeneous anode consumption, because of anode design, will occur. If the reduction cell and the anode are designed and will run with k ₀, m, and n values that result in l ₃ ≠ l ₂ in Eq. [7], inhomogeneous consumption of the anode take place and a difference in the ACD appears. Equation [7] can be used in an anode design to reduce the ACD when the bath effects on the ACD are isolated (m and n are set to constants).

The bath conductivity relation n is defined with virtual conductivities. We can express this relation with real physical properties. It is mainly given by phenomena such as surface anode overvoltage and the presence of bubbles in the bath caused by formation of CO₂. From Figure 2, a real physical expression for n can be derived from the voltage drops over each resistance in the bath.

$$ {\frac{{U_{{{\text{ba}}2}}^{\prime } }}{{U_{{{\text{ba}}3}}^{\prime } }}} = {\frac{{U_{{{\text{ov}}2}} + U_{{{\text{bu}}2}} + U_{{{\text{ba}}2}} }}{{U_{{{\text{ov}}3}} + U_{{{\text{bu}}3}} + U_{{{\text{ba}}3}} }}} $$

(8)

Equation [8] can further be expressed by resistances and current densities[7] shown in Eq. [7].

$$ {\frac{{{\frac{{\left( {L - l_{2} } \right)J_{2} }}{{\sigma_{{{\text{ba}}2}}^{\prime } }}}}}{{{\frac{{\left( {L - l_{3} } \right)J_{3} }}{{\sigma_{{{\text{ba}}3}}^{\prime } }}}}}} = {\frac{{{\frac{{{\text{R}}T}}{{1.08{\rm F}}}}\ln \left( {{\frac{{J_{2} }}{{J_{0} }}}} \right) + {\frac{{d_{{{\text{b}}2}} J_{2} }}{{\sigma_{{{\text{ba}}2}} \left( {1 - \phi_{2} } \right)}}} + {\frac{{\left( {L - l_{2} - d_{{{\text{b}}2}} } \right)J_{2} }}{{\sigma_{{{\text{ba}}2}} }}}}}{{{\frac{{{\text{R}}T}}{{1.08{\rm F}}}}\ln \left( {{\frac{{J_{3} }}{{J_{0} }}}} \right) + {\frac{{d_{b3} J_{3} }}{{\sigma_{{{\text{ba}}3}} \left( {1 - \phi_{3} } \right)}}} + {\frac{{\left( {L - l_{3} - d_{b3} } \right)J_{3} }}{{\sigma_{{{\text{ba}}3}} }}}}}} $$

(9)

where R is the universal gas constant, F is the Faraday constant, J ₀ is the limiting current density in the surface overvoltage term, and d _b the bubble layer thickness, which has a tendency to decrease with current in an electrolysis cell.[7] The bubble coverage ϕ increases with the current density and isolates the anodes’ wear surface with bubbles in a higher degree.[8]

We rearrange Eq. [9] to get an equation for n with real physical properties that can be used experimentally.

$$ n = {\frac{{\sigma_{\rm ba3}^{\prime } }}{{\sigma_{\rm ba2}^{\prime } }}} = {\frac{{\left( {L - l_{3} } \right)J_{3} }}{{\left( {L - l_{2} } \right)J_{2} }}}\left[ {{\frac{{{\frac{RT}{1.08{\text F}}}\ln \left( {{\frac{{J_{2} }}{{J_{0} }}}} \right) + {\frac{{d_{\rm b2} J_{2} }}{{\sigma_{\rm ba2} \left( {1 - \phi_{2} } \right)}}} + {\frac{{\left( {L - l_{2} - d_{\rm b2} } \right)J_{2} }}{{\sigma_{\rm ba2} }}}}}{{{\frac{RT}{1.08{\text F}}}\ln \left( {{\frac{{J_{3} }}{{J_{0} }}}} \right) + {\frac{{d_{\rm b3} J_{3} }}{{\sigma_{\rm ba3} \left( {1 - \phi_{3} } \right)}}} + {\frac{{\left( {L - l_{3} - d_{\rm b3} } \right)J_{3} }}{{\sigma_{\rm ba3} }}}}}}} \right] $$

(10)

The expression for n can also be modified and include extra effects like anodic and cathodic concentration overvoltage in the bath. The voltage drops from these effects must be added to the right side of Eq. [8], and a modified expression for n is derived from the extended equation (an extra resistance in each branch in the left DC circuit in Figure 2 will appear). We can also simplify Eq. [10] if the surface overvoltage term is linearized. The current densities J ₂ and J ₃ in Eq. [10] will be omitted.

The anode-bath conductivity relation, m, has also a virtual component in its expression. This can also be represented with physical parameters by Ohms law. From U = RI, $R = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sigma A}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma A}$}},$ and using Figure 2, the physical expression for m is shown in Eq. [11].

$$ m = {\frac{{\sigma_{\text{an}} }}{{\sigma_{{{\text{ba}}2}}^{\prime } }}} = {\frac{{\sigma_{\text{an}} A_{\text{an}} U_{{{\text{ba}}\_{\text{meas}}}} }}{{ACD_{\text{ref}} I_{\text{an}} }}} $$

(11)

The area A _an is the anode wear surface, σ _an is the anode conductivity, ACD _ref = L − l ₂ the reference ACD, I _an is the electrical current through one anode, and U _{ba_meas} is the measured/calculated voltage drop between the anode and the metal. The real conductivity of the bath is normally around 200 to 300 S/m. The total virtual conductivity of the bath $\sigma_{rm ba}^{\prime } ,$ which also includes surface overvoltage and bubble overvoltage will be much less (Figure 2). For example, a conservative cell with ACD _ref = 0.04 m and I _an = 8.000 A is approximately m ≈ 195. There is a different m for each aluminum plant, and it depends on how the manager decides to run the cell. For a current increase project in a plant, the reference ACD will be decreased. Typical values[9] can be ACD _ref = 0.03 m and a chosen I _an = 10,000 A. This results in m ≈ 220 from Eq. [11].

In the numerical study, k ₀ will be determined and the results will be linked to the variation in the ACD in Eq. [7] with specific values on m and n. It is not the intention of this article to calculate m and n for many different aluminum reduction cells. The purpose of this study is to define the parameters and illustrate them with one cell solution (m = 200, ACD _ref = 0.04 m).

Parametric Implementation of Anode Conductivity Gradients

It is well known that the physical properties of the carbon anode are inhomogeneous. There is a need to systemize these properties so that parametric numerical studies on the anode gradients can be performed. The parameters that describe the degree of inhomogeneous material properties will be used to study how they will affect k ₀. A six-parametric equation, which is shown in Eq. [12], has been proposed to describe the gradient in 3D. Electrical conductivity and all other properties that correlate well with the conductivity can be described with the parametrical equation. The equation was developed with fewest possible parameters for describing a realistic gradient of the physical property from laboratory test data.[10] The anode data from the core analyses show an orthotropic property in the electric resistivity. In the forming process of the anode from the paste plant, the anode is mainly compacted by vibration. With coke particles of an aspect ratio lower than unity, the vibration will orient the particles in a horizontal direction, normal to the direction of vibration. This can be the main reason that the resistivity in horizontal direction is lower than in the vertical direction; the number of particles in the horizontal direction will probably be lower than in the vertical direction. The experimental data also show that the resistivity increases further away from the walls of the mold of vibration, especially in the upper part of the anode. A skewed filling of the anode paste in the mold of vibration will also produce a skewed anode resistivity. Segregation of coke particles in the mixing stage in the paste plant also contributes to larger resistivities at local areas in the anode.

The equation is developed so that the average value of the physical property is placed in one term ρ ₀. The other terms are deviatory parts without the average value component. The other parts are used to describe the inhomogeneous material data. The terms with A parameters describe the nonlinear gradients, and the terms with the B parameters describe the linear gradients.

$$ \begin{aligned} \rho \left( {x,y,z} \right) & = \rho_{0} + A_{0y} \left( {\frac{z}{h}} \right)^{2} \left[ {g(y) - \int\limits_{0}^{b} {g(y)dy} } \right] + \left( {A_{01x} \left( {\frac{z}{h}} \right)^{2} - A_{02x} \left( {1 - \frac{z}{h}} \right)^{2} } \right)\left[ {f(x) - \int\limits_{0}^{l} {f(x)dx} } \right] \\ & \quad + \left( {\frac{z}{h}} \right)^{3} \left[ {{\frac{{2B_{0y} }}{b}}y - B_{0y} + {\frac{{2B_{0x} }}{l}}x - B_{0x} } \right] + {\frac{{2B_{0z} }}{h}}z - B_{0z} \\ \end{aligned} $$

(12)

The dimensions b, h, and l are the width, height, and length of the anode, respectively. The x axis is along l, y axis along b, and z axis along h. The term ρ ₀ is the average value of the physical parameter, B _0x is the slope of a linear function in the x direction, B _0y the slope of a linear function in the y direction, B _0z is the slope of a linear function in the z direction, A _01x is the amplitude of a nonlinear function in the x direction in the anode top, A _02x is the amplitude of a nonlinear function in the x direction in the anode wear surface, A _0y is the amplitude of a nonlinear function in the y direction, f(x) is the nonlinear function describing the nonlinear variation in the x direction, and g(y) is the nonlinear function describing the nonlinear variation of the anodes physical property in the y direction.

The nonlinear functions f(x) and g(y) can be found by curve fitting from the carbon core analysis. In the work described in this article, the functions is set to $f(x) = \sin \left( {\pi \frac{x}{l}} \right)$ and $g(y) = \sin \left( {\pi \frac{y}{b}} \right).$ We then have $\int_{0}^{l} {\sin \left( {\pi \frac{x}{l}} \right)dx = {\frac{2l}{\pi }}}$ and $\int_{0}^{b} {\sin \left( {\pi \frac{y}{b}} \right)dy = {\frac{2b}{\pi }}.}$

Because the longitudinal anode slots are studied here, the most interesting parameters for resistivity/conductivity gradients in the anode are A _0y and B _0y from Eq. [12]. For the numerical analyses, only the parameters A = A _0y , and B = B _0y were used for parametric numerical study of the material. The values of A and B used in the numerical analysis are shown in Figure 3.

Fig. 3

Electrical resistivity in the anode as function of the anode width, 15 cm under the anode top. In the numerical study, four different A, B parametric value pairs was chosen: (0,0), (0,4000), (4000,0), and (4000,4000). The value pair (0,0) represents an anode with a constant homogenous resistivity for each direction

In the electrolysis bath, we have a maximum thermal gradient mainly in the z direction in the anode. A typical temperature range in the z direction of the anode is from 673 K (400 °C) in the top to 1233 K (960 °C) in the wear surface. The resistivity of the anode will decrease by approximately 1 μΩm pr. 373 K (100 °C)[12] in this range. Because we only have an electric FEM, the parameter B _0z in Eq. [12] can be used to verify the effect of the thermal contribution on k ₀ by having a decreasing average resistivity from top to bottom in the anode. In the horizontal plane in the anode, the temperature range in the anode is much smaller than for the z direction. It can only contribute to a change in resistivity by a maximum of 2 to 3 μΩm in the steady state. This is less than the ranges of the A and B parameters from Figure 3. We should keep this thermal effect in mind when we study the current distribution with an electric FEM.

Modeling Procedures

The 2D model was developed mainly to find typical variations in the k ₀ parameter from different anode dimensions. The conductivity gradients of the anode were also implemented in the model by the six-parameter equation to evaluate the effect on the k ₀ parameter.

Geometry and Dimensions

The parameter, k _0, was found with different slot depths, slot positions and stub hole dimensions β, γ, and δ as shown in Table I. For each slot and stub design, the current entered the anode in four ways (i ₀ to i ₃), as described in Figure 4, so that k ₀ = k ₀, and i) was found numerically.

Table I Chosen Anode Stub and Slot Design in the FE Analysis*

Fig. 4

Path of the electrical current in the stub–anode interface. The current enters the anode from the stub hole in four ways in the FE analyses. For current input setting i ₀, it enters the upper-half area of the conic anode stub hole wall; with i ₁ it enters the whole conic stub hole wall, with i ₂ the current enters the bottom plus the whole conic stub hole wall, and for i ₃ the current enters only the bottom of the stub hole

The stub has a conic angle and the radius of the hole increases downward to the bottom of the hole, d ₁ (Figure 1). This is a typical machined stub hole made after the anode baking furnace process.[11] In the numerical analyses, the contact resistance has been neglected (zero voltage drop from cast iron to anode and from yoke to cast iron when the contact is established). The current has been parameterized to enter in four different ways: from the situation where the current enters the bottom of the stub hole, to the opposite situation where the current enters the upper part of the stub hole wall. Table I shows the different geometrical anode slot and stub dimensions for numerical study and how the current enters the anode in the numerical analyses. Each geometrical configuration is tested with different gradients of anode resistivity with the four combinations on A and B as described previously.

An ACD of 0.04 m was used in the FE analyses (distance from the anode wear surface to the metal pad). The ACD was constant during the analysis. The metal pad was defined as the boundary of ground.

Mesh, Material Data, and Boundary Conditions

The conductive Media DC module in the FE software, COMSOL 3.4 (COMSOL, Inc., Burlington, MA), was used with 2D quadratic Lagrange elements. A mesh was defined for the whole domain with maximum element size scaling factor = 0.08, element grow rate = 1.2, mesh curvature factor = 0.25, mesh curvature cutoff = 0.0003, and resolution of narrow regions = 1. This gave an element number of 75,000 for the whole domain shown in Figure 5.

Fig. 5

The 2D domain consists of the subdomains yoke, cast iron, anode, and bath. The current enters from the top of the yoke and penetrates down to the metal pad defined as the boundary of ground. All outer boundaries got an electrical insulated property. The internal boundaries were defined with continuity. The current lines on the figure are shown for current setting i ₀, which is described in Table I

The material data for the four subdomains (Figure 5) are as follows:

• Yoke: Electrical conductivity of 5E6 S/m.

• Cast iron: Electrical conductivity of 2E6 S/m.

• Anode: In the subdomain setting in COMSOL the anode was defined orthotropic. In the x and y direction, the value of conductivity was set by the expression in Eq. [12] with a mean conductivity, ρ ₀ = 20,408 S/m, and for the z direction the value was set to the expression in Eq. [12] by the mean conductivity of ρ ₀ = 19,230 S/m. The gradient parameters A = A _0y and B = B _0y were used in the numerical study of the material and set to values shown in Figure 3. The other gradient terms of Eq. [12] were omitted in the 2D study. The parameters A (nonlinear gradient), B (linear gradient), and ρ ₀ (mean value) were defined in the list of constants in COMSOL.

• Bath: The electrical conductivity of 95 S/m (the surface overvoltage and bubble coverage) reduces the value compared with the bath’s real conductivity of 200 to 300 S/m. This value was tuned to get a voltage loss over the whole domain of 3.6 V. The anode-bath conductivity relation m (Eq. [11]) was therefore numerically found and set to m = 19,000/95 = 200 for the analysis.

The data for estimating k ₀ were found on the boundary 2 cm above the bath shown in figure 5 (or 17 cm above the anode wear surface). The current density J ₃ is found by integrating the current along the boundary crossing the outer leg of the anode. The current density J ₂ is found by integrating the current along the boundary crossing the inner leg of the anode. The widths of the anode legs are defined by the position of the longitudinal slots in the anode. The k ₀ parameter was calculated by Eq. [1].

Results and Discussion

The parameter k ₀ was found as function of slot position, slot depth, stub size, and the current input setting of the anode (k ₀ = k ₀[β, γ, δ, and i]). Figure 6 shows the results. Within realistic designs of the anode (Table I), k ₀ can change from 1.06 to 1.20.

Fig. 6

The left plot for the stub dimension, δ = 3.18, shows k ₀ as function of slot position g, slot depth b, and electrical current input setting i ₀ to i ₃ (Table I) for an orthotropic homogenous anode material (A = B = 0). The k ₀ parameter decreases mainly with decreasing distance between the longitudinal slots (decreasing g), deeper slots (decreased b), and with a greater part of the current entering the bottom of the stub hole (toward i ₃). For every slot position g, the parameter k ₀ is decreasing with electrical current input settings, from i ₀ to i ₃, for a specific slot depth. The right plot shows the corresponding voltage drops for the electrical current input settings i ₀, i ₁, i ₂, and i ₃ along the x axis

The current input setting, slot depth, and slot position (i, β, and γ) all influence the k ₀ (Figure 6). The variation in the stub hole δ has a minor effect on k ₀, which increases slightly with decreasing δ (a decrease of the stub hole extension of δ = 3.14 to δ = 3.20 decreases k ₀ within 0.01 for every parametric study). Figure 6 shows the k ₀ for δ = 3.18.

With the electrical current entering the bottom of the anode stub hole (i ₂ and i ₃ setting), a greater part of the current will travel through leg 2 of the anode. The current distribution in the anode will be distributed more homogeneously and k ₀ will be decreased. In a 3D model, the variation in k ₀ resulting from the current input settings, i ₀ to i ₃, would have been slightly reduced, but it would have kept the same trend as shown in the left plot in Figure 6. The current input setting i ₀ in the 2D model, where the current enters the upper conic side walls of the stub hole, is the case in 3D where the current enters this way for each position along the anode length. The current input setting i ₃ in 2D, where the current enters the bottom of the stub hole, will be the situation in 3D where the current enters this way for every position along the anode length.

For a deeper anode slot (lower β) the variation in k ₀ is greater than for a shorter slot (left plot in Figure 6). This means that different slot positions and current input settings create larger variation in k ₀ when the slots are deeper. The best case k ₀ = 1.06 has a slot position of γ = 1, slot depth of β = 1.4, and electrical current input setting i ₃. This is an anode with deeper slots closer to each other and with an electrical current entering the anode in the bottom of the anode stub hole. The worst case, k ₀ =1.20, has a slot position of γ = 1.36, slot depth of β = 1.75, and electrical current input setting i ₀. This is an anode with shorter slots further away from each other and with electrical current entering in the upper half region of the conic stub hole wall. The current density distribution along the boundary 2 cm above the bath level for the best and worst k case is shown in Figure 7.

Fig. 7

Electrical normal current density distribution over the anode width along the boundary 2 cm above the bath for the best k case (k ₀ = 1.06 for γ = 1, β = 1.4, i = i ₃, δ = 3.20) and worst k case (k ₀ = 1.20 for γ = 1.36, β = 1.75, i = i ₀, and δ = 3.14)

The worst k case can induce lot of implications. From initial to steady state, the outer legs of the anode will be shorter than the center leg because the chemical processes consumes the anode at a higher rate where the current density is higher. This creates an unnecessary variation in the ACD and prevents the manager of the plant to lower the average of the ACD by current increase action programs to increase the metal capacity.

With k ₀ found previously and with a simulated cell setting of m = 200, we can set these values into Eq. [7] and study how an initial current distribution in the anode can affect the ACD. Figure 8 describes the critical n (n _c ) we must have for keeping l ₂ = l ₃ for different k ₀ when m = 200, using Eq. [7].

Fig. 8

The critical n for different k ₀ to keep l ₂ = l ₃ so that no difference in the ACD will occur. The anode-bath conductivity relation is set to m = 200, ACD_ref = 0.04 m, and l ₂ = 600 mm in Eq. [7]

The worst case of anode design k ₀ = 1.20 demands a bath conductivity relation n = 0.83 to avoid a variation in the ACD by k ₀. If n = 0.9, then it is observed from Figure 9 that ${\raise0.7ex\hbox{${l_{2} }$} \!\mathord{\left/ {\vphantom {{l_{2} } {l_{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${l_{3} }$}} = 1.006.$ With l ₂ = 600 mm, we have l ₃ = 596.5 mm, which means a difference in the ACD of 3.5 mm. The values of k ₀, which are found from realistic anode designs, can easily induce a difference in the ACD around 10 pct of its value if the critical n is not reached.

Fig. 9

The relation l ₂/l ₃ as function of initial anode current distribution k ₀ and the bath conductivity relation n for a reference anode height, l ₂ = 600 mm, m = 200, and ACD_ref = 0.04 m

We should keep in mind that the k ₀ found from the numerical analyses are based on average values of current densities. In real cases, if we take into account inhomogeneous frozen bath on the anode wear surface, the “real k” can be much higher than the model shows. It can also increase by asymmetric electrical coupling of the yoke to the anode with cast iron. The electrical coupling between the stub holes in one anode can also differ and increase k ₀. A real k ₀ of 1.4 demands a bath conductivity relation n < 0.71 if a variation in the ACD is to be avoided (Figure 8). Another point to remember is that the bubble coverage under the anode wear surface as function of anode current density has a lower slope for current densities above 1 A/cm² than for current densities beneath 1 A/cm².[8] This means that the bath conductivity relation n is larger for high-amperage cells. The risk is higher such that the initial electrical current distribution in the anode creates variations in the ACD for a high-amperage cell.

For each parametric setting in the numerical analyses, the voltage drop in the anode was calculated by integrating the resistive heat loss over the anode. The lowest anode voltage drop is found when a greater part of the anode current enters the bottom of the stub hole (i ₂ and i ₃ setting in Figure 6). Voltage drops up to 80 mV can be saved.

The effects on voltage drop from slot design are strongest for the electrical current input setting i ₃. Even for this setting, the model shows a minor increase of with deeper slots (decreased β from Figure 6).

Electrical anode resistivity gradients with A = B = 4000 S/m in Eq. [12] can only increase k ₀ with 0.01 (Figure 10). This value is under 10 pct of the variation in k ₀. The effects from anode geometry and current input settings explain the rest of the variation in k ₀. The A, B value pairs (4000,0) and (0,4000) gives more or less the same k ₀ value. The anode voltage drop is specially affected by anode resistivity gradients for the current input setting i ₀, where resistivity gradients of A = B = 4000 S/m can increase the anode voltage drop by 10 mV (Figure 9). The other anode current input settings for such resistivity gradients can only create a 5-mV increase by the 2D model. It is specially the nonlinear gradient A that contributes to the extra voltage drop. If we add the linear gradient B, this will not create any extra voltage drop.

Fig. 10

The left figures show k ₀ as function of the resistivity gradients of the anode for two different anode designs, the best k case, and the worst k case. The right plots show the corresponding voltage drops. Both k ₀ and the voltage drop are plotted with the electrical current input setting i ₀ to i ₃ on the x axis. There are no anode resistivity gradients when A = B = 0, but the orthotropic property of the material is present for each A, B value pair

Conclusions

For realistic anode designs, the k ₀, describing the degree of initial inhomogeneous electrical current distribution in the anode, can range from 1.06 to 1.20. If the anode is designed with a k ₀ = 1.20, the bath conductivity relation n should be less than 0.83 for the analyzed cell if the variation in the ACD is to be avoided. The best k case (low k ₀) describes an anode with deeper slots closer to each other and with an electrical current entering the anode in the lower parts of the anode stub hole. The k ₀ values found from numerical analyses are based on the average values of current densities in the anode. In real cases, if we take into account inhomogeneous frozen bath on the anode wear surface, the “real k ₀” can be much higher than the model shows. It can also increase by asymmetric electrical coupling of the yoke to the anode with cast iron. A real k ₀ of 1.4 demands a bath conductivity relation n < 0.71 for the analyzed cell if a variation in the ACD is to be avoided. For high-amperage cells, the bubble coverage as a function of anode current density has a lower slope above 1 A/cm² than for current densities beneath. This increases n, and the risk is higher for the initial current distribution in the anode to affect the variation in the ACD.

The anode voltage drop was found for each anode design in the numerical study. The 2D model showed that voltage drops over 50 mV can be saved if a greater part of the current is entering the bottom of the stub holes instead of the upper part of the stub hole walls. Different slot designs have minor effect on the voltage drop. The 2D FEM can only trace a 5-mV increase when the slot becomes deeper.

The electrical anode resistivity gradients within the defined gradients of A = B = 4000 S/m creates a minor increase in k ₀ of 0.01, but they can increase the anode voltage drop by 10 mV for current input setting i ₀ (current enters upper part of the stub hole walls in the 2D model). It is the nonlinear anode gradient A that contributes to the increased voltage drop.