1 Introduction

Teleportation [5] is probably the most spectacular application of quantum entanglement [12]. Nowadays, thanks to the rapid development of recent experimental work [3, 23], teleportation is a part of modern science rather than fiction. Twenty years after inventing entanglement-based teleportation of qubits, the idea is often labeled as “simple.” There are two parties: Alice and Bob, sharing a bipartite entangled qubit state \(\chi _{AB}\), the resource state, one part in Alice’s and one in Bob’s hands. Alice is going to send her qubit \(\rho _A\) to Bob. She performs a Bell state measurement on a pair consisting of the qubit which is going to be sent and on her “half” of the resource state. The outcome of the measurement, communicated via classical channel to Bob, allows him to transform his qubit \(\rho _B\) and reproduce initial Alice’s qubit via suitable and well-defined procedure \(\rho _B\rightarrow \rho _A\).

Performing realistic teleportation, one is faced with omnipresent decoherence [16]; especially the resource state \(\chi _{AB}\), waiting for being used, suffers from interaction with environment and resulting noise. In such a situation, despite related information loss, effective teleportation is not excluded [2, 6, 11, 13, 16, 18]. Teleportation using a mixed state as a resource can be formalized in terms of a generalized depolarization channel [6]:

$$\begin{aligned} \rho _{B}&= \varLambda (\chi {_{AB}}) \rho _{A}. \end{aligned}$$
(1)

where, for an arbitrary two-dimensional matrix \(\rho \),

$$\begin{aligned} \varLambda (\chi {_{AB}})\rho&= \sum _{i=0}^3 \text{ Tr }[B^i \chi {_{AB}}]\sigma _i\rho \sigma _i, \end{aligned}$$
(2)

and \(B^i\) are the Bell states associated with the Pauli matrices \(\sigma _i\) by the relation

$$\begin{aligned} B^i&= \left( \sigma _0\otimes \sigma _i\right) B^0\left( \sigma _0\otimes \sigma _i\right) , i=1,2,3, \nonumber \\ \sigma _0&= {\mathbb {I}},\,\, \sigma _{1,2,3}=\sigma _{x,y,z} \end{aligned}$$
(3)

with

$$\begin{aligned} B^0&= \frac{1}{2}\left( |01\rangle +|10\rangle \right) \left( \langle 01|+\langle 10|\right) \!. \end{aligned}$$
(4)

In this paper, we assume that the decoherence affecting \(\chi _{AB}\) is due to thermal environments. We also assume that the decoherence is bilocal, Markovian, and can be described in terms of the rigorous Davies approximation [1]. We show that there are environments such that fidelity of the corresponding teleportation channel Eq. (1) can be independent of temperature of the environment. There are also certain conditions imposed on both environment and \(\rho _A\) where the fidelity of teleportation channel is enhanced by the growth of the temperature.

The paper is organized as follows: in Sect. 2, we briefly present the properties of decoherence model used in our studies. In Sect. 3, we analyze the fidelity of teleportation, focusing on conditions leading to temperature independence. In Sect. 4, we consider the unitary limit in which at least a part of the system is perfectly isolated from its environment. Results and conclusions are summarized in the last section.

2 Model of decoherence

A natural source of decoherence affecting quantum systems is their environment. Here, we assume that two qubits initially in a state \(\chi _{AB}\) shared by Alice and Bob interact with their own environments \(E_A\) and \(E_B\). As Alice and Bob can be far away from each other, we do not assume any direct interaction between their qubits. Hence, Hamiltonian of the total system is given by

$$\begin{aligned} H&= H_A+H_B+H^{int}_{AE_A}+H^{int}_{BE_B} \end{aligned}$$
(5)

We also assume that qubits \(A\) and \(B\) are identical:

$$\begin{aligned} H_A&= H_B=\frac{\omega }{2}(|1\rangle \langle 1|-|0\rangle \langle 0|) \end{aligned}$$
(6)

Moreover, we assume that the interaction between qubits and their environments is weak and satisfies requirements for applying Davies weak coupling approach [1] for constructing their reduced (with respect to environments) dynamics. The Davies approach is dedicated to constructing explicitly the generator of a completely positive (strictly Markovian) semigroup describing reduced (with respect to the environment) dynamics of open systems in terms of parameters of the microscopic Hamiltonian of the full system [1]. Davies semigroups are rigorously and consistently derived from microscopic models of open systems. They satisfy most of the desired thermodynamic and statistical–mechanical properties such as the detailed balance condition [1]. Davies approximation has recently been applied to studies of various problems in quantum information and physics of open quantum systems including entanglement dynamics [14], quantum discord [7, 10], or properties of geometric phases of qubits [8].

Here, instead of using full power of Davies semigroups, we consider Davies maps [20], being certain elements of Davies dynamical semigroups. With the subscripts \(A\) and \(B\) denoting Alice’s and Bob’s parts (qubits and environments) of the system, respectively, and for \(\chi _{AB}(0)=B^0\):

$$\begin{aligned} \chi _{AB}(t)&= [D_A\otimes D_B] B^0 \end{aligned}$$
(7)

where the Davies map \(D=D(p,A,G,\omega ,t)\) reads as follows [20]:

$$\begin{aligned} D|1\rangle \langle 1|&= [1-(1-p)(1-e^{-At})]|1\rangle \langle 1|\nonumber \\&+\,(1-p)(1-e^{-At})|0\rangle \langle 0| \end{aligned}$$
(8)
$$\begin{aligned} D|1\rangle \langle 0|&= e^{i\omega t -Gt}|1\rangle \langle 0| \end{aligned}$$
(9)
$$\begin{aligned} D|0\rangle \langle 1|&= e^{-i\omega t -Gt}|0\rangle \langle 1| \end{aligned}$$
(10)
$$\begin{aligned} D|0\rangle \langle 0|&= p(1-e^{-At})|1\rangle \langle 1|\nonumber \\&+\,[1-p(1-e^{-At})]|0\rangle \langle 0| \end{aligned}$$
(11)

where \(p\in [0,1/2]\) is related to the temperature (\(k_B=1\)) via

$$\begin{aligned} p&= \exp (-\omega /2T)/[\exp (-\omega /2T)+\exp (\omega /2T)]. \end{aligned}$$
(12)

The parameter \(p\) Eq. (12) can be interpreted as a rescaled temperature as it ranges from \(p=0\) for zero temperature limit up to \(p=1/2\) for an infinite temperature. Parameters \(A = 1/\tau _R\) and \(G = 1/\tau _D\), interpreted in terms of spin dynamics [15], are related to the energy relaxation time \(\tau _R\) and the dephasing time \(\tau _D\), respectively [20]. Decoherence in Eq. (7) is bilocal, i.e., it cannot enhance the entanglement of \(\chi _{AB}(t)\). It is reasonable as the qubits forming \(\chi _{AB}\) are usually well separated in space.

Let us notice the following asymptotic property of Davies maps, which transform any qubit state \(\rho \) in long time limit into equilibrium Gibbs state:

$$\begin{aligned} \lim _{t\rightarrow \infty }D(p,A,G,\omega ,t)\rho =p|1\rangle \langle 1|+(1-p)|0\rangle \langle 0| \end{aligned}$$
(13)

In the Davies approach, \(A\) and \(G\) obey the inequalities [15]

$$\begin{aligned} G&\ge A/2 \ge 0\end{aligned}$$
(14)

guarantying that the Davies map is a trace-preserving completely positive map.

The limiting case \(A=0\) and \(G\ne 0\) corresponds to pure dephasing without dissipation of energy. The opposite case, i.e., \(G=0\) and \(A\ne 0\), cannot be physically realized as the dissipation of energy is necessarily accompanied by finite dephasing. It is also reflected in the inequality (14). Let us notice that an explicit temperature dependence (via \(p\)) of the Davis map Eq. (8) is accompanied by implicit temperature dependence of energy relaxation and dephasing time [1]. However, here we assume that the potential implicit temperature dependence of Davis maps can be neglected and both \(A\) and \(G\) are independent parameters. Such an assumption can clearly become questionable, e.g., in high-temperature regime.

Teleporting channel Eq. (1) using as a resource \(\chi _{AB}\) from Eq. (7) reads as follows:

$$\begin{aligned} \varLambda (\chi {_{AB}})|1\rangle \langle 1|&= (1-x)|1\rangle \langle 1|+x|0\rangle \langle 0| \end{aligned}$$
(15)
$$\begin{aligned} \varLambda (\chi {_{AB}})|1\rangle \langle 0|&= e^{-(G_A+G_B)t}|1\rangle \langle 0| \end{aligned}$$
(16)
$$\begin{aligned} \varLambda (\chi {_{AB}})|0\rangle \langle 1|&= e^{-(G_A+G_B)t}|0\rangle \langle 1| \end{aligned}$$
(17)
$$\begin{aligned} \varLambda (\chi {_{AB}})|0\rangle \langle 0|&= x|1\rangle \langle 1|+\,(1-x)|0\rangle \langle 0| \end{aligned}$$
(18)

where

$$\begin{aligned}&x=(p_A+p_B-2p_Ap_B)\left( 1+e^{-(A_A+A_B)t}-e^{-A_At}-e^{-A_Bt}\right) \nonumber \\&\quad \quad +\frac{1}{2}\left( e^{-A_At}+e^{-A_Bt}\right) \end{aligned}$$
(19)

Let us notice that the channel \(\varLambda (\chi _{AB})\) defined in Eq. (1) and Eqs. (15–18) is truly teleporting as long as \(\chi _{AB}\) remains entangled. If time \(t\) exceeds the time of potential decoherence-induced entanglement sudden death of \(\chi _{AB}\), the channel \(\varLambda (\chi _{AB})\) remains a well-defined quantum depolarization channel but it has not much to do with the teleportation.

3 Fidelity of the teleporting channel

The “output–input” fidelity \(F\) [4] is a natural measure of quality of a quantum channel. It reduces to an overlap between states provided that at least one of the states used in its calculation is pure [17].

In the following, we assume that the input qubit which Alice is going to teleport is in a pure state

$$\begin{aligned} \rho _A&= |\Psi \rangle \langle \Psi |\nonumber \\ |\Psi \rangle&= \cos (\theta /2)|1\rangle +e^{i\phi }\sin (\theta /2)|0\rangle \end{aligned}$$
(20)

As the input state Eq. (20) is pure, fidelity of the teleporting channel Eq. (1) takes the simpler form [17] and it quantifies an overlap of the final state \(\rho _{B}(t)\) and the initial state \(\rho _{A}\):

$$\begin{aligned} F(t)&= \text{ Tr }\left[ \rho _{B}(t) \rho _{A}\right] . \end{aligned}$$
(21)

If teleportation is perfect, the final state is the same as the initial state so that the fidelity \(F=1\).

For quantum channel given by Eq. (1) and Eqs. (15–18), it is possible and straightforward to obtain analytic results for corresponding fidelity. Here, to avoid presenting large formulas, we limit our discussion to several specific and, in our opinion, most interesting cases.

Let us start with a simplified setup when the parameters describing environments affecting Alice’s and Bob’s part of the resource state \(\chi _{AB}\) are identical, \(A_A=A_B=A\), \(G_A=G_B=G\), except that one of environments, say \(E_B\), is cooled down to \(p_B=0\). The fidelity of the teleporting channel Eq. (1)

$$\begin{aligned}&F= \frac{1}{4}+\frac{p}{2}\left( 1+\cos (2\theta )\right) +\frac{1}{4}e^{-2Gt}\left( 1-\cos (2\theta ) \right) \nonumber \\&\quad \qquad +\frac{1}{2}e^{-At}\left( 1-p\right) \left( 1+\cos (2\theta )\right) \end{aligned}$$
(22)

depends both on the initial state (via \(\theta \) but not via \(\phi \)) and all the remaining parameters (including temperature in \(p=p_A\)) of the environment \(E_A\). In the (typical) case when the input state Eq. (20) is unknown but pure, one can obtain from Eq. (22) mean fidelity (averaged over Bloch sphere):

$$\begin{aligned} <F>\,=\frac{1}{4\pi }\int _0^{2\pi } d\phi \int _0^\pi \sin (\theta )F(\theta ) \end{aligned}$$
(23)

An average fidelity related to Eq. (22) reads as follows:

$$\begin{aligned} <F>&= (\frac{1}{3}-\frac{2}{3}p)e^{-At}+\frac{1}{3}(e^{-2Gt}+pe^{-2At})+\frac{1}{3}(p+1) \end{aligned}$$
(24)

To quantify the entanglement of the resource state \(\chi _{AB}\), we use negativity

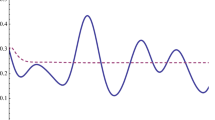
$$\begin{aligned} N[\chi _{AB}]=\frac{1}{2}\sum _i\left( |\lambda _i|-\lambda _i\right) \end{aligned}$$
(25)

where \(\lambda _i\) are eigenvalues of a partially transposed density matrix \(\chi _{AB}\) of a bipartite system [12]. In panel (a) [panel (b)] of Fig. (1), we present fidelity Eq. (22) [averaged fidelity Eq. (24)] of teleporting channel calculated for the input state Eq. (20) with \(\theta =\pi \) in energy-relaxing regime \(A=2G\). In panel (c) of Fig. (1), we present negativity of the corresponding resource state \(\chi _{AB}\). As there is energy dissipation present in the system (\(A\ne 0\)), one always expects entanglement sudden death for any choice of parameters (contrary to pure dephasing when the negativity can decay exponentially [9]). It is intuitively clear that with growing temperature (\(p\)), the time when entanglement death occurs becomes shorter and shorter.

However, even such a very specific example as considered here exhibits apparently counterintuitive property: fidelity decay becomes slower with growing temperature \(p\). It is an example of a possibility of enhancement of teleportation fidelity induced by local noise [24]. Such an enhancement occurs here in a quantum model of physically well-understood framework of the Davies theory of open systems and seems to be generic as it occurs not only for typical fidelity, as presented in panel (b) of Fig. (1), but also for randomly chosen values of \(\theta \) (not presented here).

Fig. 1
figure 1

(Color online) a Fidelity of teleporting channel Eq. (1) and Eqs. (15–18) calculated for different values of \(p=p_A\) and \(p_B=0\) with \(A_A=A_B=2G_A\) and \(G_A=G_B=1\). Initial state Eq. (20) is chosen for \(\theta =\pi \). b Average fidelity Eq. (24) presented for the same parameters as in panel (a). c Negativity Eq. (25) of the corresponding resource state \(\chi _{AB}\) given by Eq. (7)

Full size image

The primary objective of our studies is to recognize regimes when the fidelity of teleportation channel Eq. (1), with Eqs. (15–18), is temperature-independent (\(p\)-independent). Let us consider general system but a specific input Eq. (20) with either \(\theta =\pi /2\) or \(\theta =3\pi /2\). The corresponding fidelity depends only on dephasing times of both environments \(E_A\) and \(E_B\):

$$\begin{aligned} F&= \frac{1}{4}+\frac{1}{4}e^{-(G_A+G_B)t} \end{aligned}$$
(26)

It is obviously and trivially temperature-independent.

It is also possible to obtain temperature-independent fidelity for arbitrary input provided that one of the environments, lets say \(E_B\), is warmed up to infinity, i.e., \(p_B=1/2\). Physically, it means of course a very high temperature of one thermostat and very weak temperature dependence with respect to the second one. Fidelity of the corresponding teleporting channel is not affected by \(p_A\):

$$\begin{aligned} F&= \frac{1}{2}+\frac{1}{4}e^{-(A_A+A_B)t}\left( 1+\cos (2\theta ) \right) + \frac{1}{4}e^{-(G_A+G_B)t}\left( 1-\cos (2\theta ) \right) \end{aligned}$$
(27)

The corresponding average fidelity reads as follows:

$$\begin{aligned} <F>&= \frac{1}{2}+\frac{1}{6}e^{-(A_A+A_B)t}+ \frac{1}{3}e^{-(G_A+G_B)t} \end{aligned}$$
(28)

Fidelity is also temperature-independent (\(p\)-independent) if one of the environments does not exchange energy with its attached qubit, i.e., when (at least) one of the environments causes pure dephasing (\(A_B=0\)) with no energy relaxation:

$$\begin{aligned} F&= \frac{1}{2}+\frac{1}{4}e^{-A_At}\left( 1+\cos (2\theta ) \right) + \frac{1}{4}e^{-(G_A+G_B)t}\left( 1-\cos (2\theta ) \right) \end{aligned}$$
(29)

Here, the temperature independence holds true for an arbitrary choice of remaining parameters of environments and initial preparation \(\rho _A\) in Eq. (20). The average fidelity

$$\begin{aligned} <F>&= \frac{1}{2}+\frac{1}{6}e^{-A_At}+ \frac{1}{3}e^{-(G_A+G_B)t} \end{aligned}$$
(30)

Let us notice that the pure dephasing serves as a good approximation of various models studied in wide range of contexts [19, 21, 22].

Relationship between temperature dependence of the fidelity and the particular choice of initial preparation is well visible in, otherwise not very interesting for teleportation, long time limit \(\lim _{t\rightarrow \infty } F\). In Fig. (2), we present asymptotic fidelity calculated for different \(\theta \) in the system with remaining parameters as in Fig. (1). Let us observe that ordering of curves at \(t=\infty \) presented in Fig. (2) is preserved in time, i.e., it is the same as for an arbitrary finite value of \(t\). Let us also notice particular character of both initial preparation with \(\theta =\pi /2\) and infinite temperature \(p_A=1/2\) leading to \(F=1/2\). In other words, teleportation of a quantum state Eq. (20) with \(\theta =\pi /2\) is as ineffective as embedding teleportation protocol in a very hot environment.

Fig. 2
figure 2

(Color online) Long time limit of fidelity \(F(\infty )=\lim _{t\rightarrow \infty } F\) calculated for different \(\theta \) and \(p=p_A\). Remaining parameters are as in Fig.  (1)

Full size image

4 Unitary limit

In this section, we consider very specific limiting case of the system considered in our work. We assume that one of the qubits, either belonging to Alice or to Bob, forming resource state \(\chi _{AB}\) is not affected by any decoherence, i.e., its evolution is purely unitary. The unitary limit of the Davis map is obtained as a limiting procedure divided into two steps. In the first step, we exclude energy dissipation. It corresponds to the limit \(A\rightarrow 0\) followed then by the second step which is a limit \(G\rightarrow 0\). Let us notice that due to the condition Eq. (14), the ordering of limits follows from physical arguments.

If an unaffected by the environment (noiseless) qubit belongs to Alice, the fidelity of corresponding teleportation channel Eq. (1) and Eqs. (15–18)

$$\begin{aligned} F_{uA}&= \lim _{G_A\rightarrow 0}\lim _{A_A\rightarrow 0}F\nonumber \\&= \frac{1}{2}e^{-(A_B+G_B)t} [e^{(A_B+G_B)t}+e^{A_Bt}(1-\cos (\theta )^2)\nonumber \\&+\,4e^{G_Bt}(1+\cos (\frac{\theta }{2})^4-\cos (\frac{\theta }{2})^2)] \end{aligned}$$
(31)

does not depend on the temperature of the environment \(E_B\) affecting Bob’s qubit. The average of fidelity Eq. (31) calculated with respect to the input state reads as follows:

$$\begin{aligned} <F_{uA}>&= \frac{1}{2}e^{-(A_B+G_B)t} \left[ e^{-(A_B+G_B)t}+ \frac{2}{3}\left( e^{-A_Bt}-e^{-G_Bt}\right) \right] \end{aligned}$$
(32)

Doing one step further and assuming no decoherence at all (i.e., evolution of both qubits forming resource state \(\chi _{AB}\) is unitary), one arrives at an expected result:

$$\begin{aligned} F_{uA,B}&= \lim _{G_B\rightarrow 0}\lim _{A_B\rightarrow 0}F_{uA} =1 \end{aligned}$$
(33)

corresponding to perfect (generic) teleportation.

Let us notice physical and practical implication of that result. In simple words, in order to obtain temperature-independent (\(p\)-independent) teleportation, it is enough to take care only on “one-half” of the resource state \(\chi _{AB}\) keeping it as far from decoherence as possible and making its evolution unitary. Fidelity of the corresponding teleportation is not affected by temperature of the environment of the second qubit undergoing Davies evolution.

5 Conclusions

Thermal noise is one of the sources of decoherence, which seem to be unavoidable in real systems. Lowering temperature is the first and natural answer to the question how to reduce such a noise. It is not always possible, and it is not always desired solution. This paper was devoted to another solution: one can operate in the regime where the system becomes independent on temperature.

We investigated the fidelity of qubit teleportation channel in the regime when the shared entangled resource state was affected by thermal fluctuations caused by independent thermal reservoirs, modeled in terms of Davis maps. There are two origins of temperature dependence of the Davis maps Eqs.  (8–11). The first is explicit, via parameter \(p\) in Eq. (12), and the second via dephasing and relaxation time entering the Davis map. We strictly limited our investigation to the first source of temperature dependence assuming the second to be negligible. Such a simplified approach allows us to avoid the details of microscopic processes inherent in a realistic model for a system–reservoir coupling. We show that there are circumstances when the fidelity becomes independent on temperature of at least one of environments. (i) Such an independence can occur provided that one of the reservoirs is a source of pure decoherence without energy dissipation. (ii) The temperature of one of the environments does not alter the fidelity of teleporting channel if the second environment is infinitely hot, or (iii) in teleportation of qubits prepared in very specific states. (iv) It is also possible to obtain temperature-independent fidelity of teleportation isolating one of qubits of the resource state from its environment. Last but not least, there is a possibility of thermal enhancement of fidelity of teleportation channel in the model which was studied in the paper. In all the investigated cases, desired features of teleportation are obtained via modification of local properties of the total system by acting only on its subsystems. The Davies model of decoherence adapted in this work, contrary to many phenomenological approaches, despite its limitations, is directly related to physical properties of the investigated model. Such a choice guarantees well-defined range of applicability of obtained results. We hope that presented studies will be helpful for further development of practical implementations of teleportation in quantum information processing.