Abstract
Human activity is drastically altering global nitrogen (N) availability. The extent to which ecosystems absorb additional N—and with it, additional CO2—depends on whether net primary production (NPP) is N-limited, so it is important to understand conditions under which N can limit NPP. Here I use a general dynamical model to show that N limitation at steady-state—such as in old-growth forests—depends on the balance of biotically controllable versus uncontrollable N inputs and losses. Steady-state N limitation is only possible when uncontrollable inputs (for example, atmospheric deposition) exceed controllable losses (for example, leaching of plant-available soil N), which is the same as when uncontrollable losses (for example, leaching of plant-unavailable soil N) exceed controllable inputs (biological N fixation). These basic results are robust to many model details, such as the number of plant-unavailable soil N pools and the number and type of N fixers. Empirical data from old-growth tropical (Hawai’i) and temperate (Oregon, Washington, Chile) forests support the model insights. Practically, this means that any N fixer—symbiotic or not—could overcome ecosystem N limitation, so understanding N limitation requires understanding controls on all N fixers. Further, comparing losses of plant-available N to abiotic inputs could offer a rapid diagnosis of whether ecosystems can be N-limited, although the applicability of this result is constrained to ecosystems with a steady-state N cycle such as old-growth forests largely devoid of disturbance.
Similar content being viewed by others
Introduction
Many ecosystems are receiving increasing amounts of nitrogen (N) deposition due to fossil fuel burning (Galloway and others 2004), and ecosystem responses to this global change depend on whether N limits net primary production (NPP). Ecosystems in which N limits NPP, which are relatively common (LeBauer and Treseder 2008), will respond to additional N deposition by taking up additional CO2 from the atmosphere, whereas those that are not N-limited will not take up additional CO2. Moreover, additional N deposition to non-N-limited ecosystems facilitates the release of the greenhouse gas nitrous oxide (N2O) (Aber and others 1989; Hall and Matson 1999, 2003) and exacerbates other environmental issues such as eutrophication and acidification (Aber and others 1989). For these and other reasons, it is critically important to understand the conditions under which N can limit NPP.
Nitrogen availability to plants is ultimately constrained by N inputs to and N losses from ecosystems. In terrestrial ecosystems, N inputs include atmospheric deposition of fixed N (that is, not N2), biological N fixation (BNF), and in rare cases rock weathering (Holloway and Dahlgren 2002). Nitrogen losses include leaching into waterways, gas losses, and erosion. Each of these inputs or losses includes many separate processes or sources. For example, BNF comes from symbioses between plants and bacteria, lichens, and a host of free-living prokaryotes; and gas losses come from denitrification, nitrification, ammonia volatilization, fire, and other processes.
Despite these complexities, grouping N inputs and losses by the degree to which they are under biotic control has advanced our understanding of N limitation. Vitousek and Reiners (1975) argued that N-limited plants should take up most or all plant-available N in the soil, drastically limiting N losses. Because abiotic inputs such as wet and dry deposition are omnipresent and essentially independent of biotic demand, they argued that plant control over N losses should render N limitation a transient phenomenon. Noting that N losses also come from plant-unavailable N pools such as recalcitrant organic molecules (Binkley and others 1992; Currie and others 1996; Hedin and others 1995; Sollins and others 1980), Hedin and others (1995) suggested that sufficiently large losses of plant-unavailable N could perpetuate N limitation.
Ecosystem models have formalized these arguments by assuming N limitation and determining conditions that prevent infinite N accumulation, typically in the context of old-growth forests largely devoid of disturbance. This approach works because we know N does not accumulate without bound in reality. If a model that assumes N limitation leads to an equilibrium, it is a decent reflection of reality. On the other hand, if it leads to infinite N accumulation, it is not a decent reflection of reality, so we conclude that the assumption of N limitation is incorrect under those conditions. DeAngelis (1992) showed in an analytical model of autotrophs and available nutrients that N accumulated infinitely when losses originated from only the available pool, whereas N accumulation was constrained when losses originated from the autotroph pool, with or without losses from the available pool. Using simulation models with plant, detritus, and available nutrient pools, Vitousek and others (1998) showed that losses via episodic disturbance such as fire or losses of plant-unavailable forms also constrained N accumulation. Menge and others (2009b) used an analytical model with plant, detritus, and available nutrient pools and a wide range of functional forms for ecosystem processes to show that losses of plant-unavailable N were necessary to prevent infinite N accumulation, but this effect only became apparent at centurial time scales.
These examples illustrate one of the challenges with classifying losses as “controllable” versus “uncontrollable” and pools as “plant-available” versus “plant-unavailable.” Autotrophs likely have some degree of control over losses from themselves, yet according to these studies these losses fit in the “uncontrollable” category. Similarly, N in a plant is certainly available to that individual, yet it falls into the “plant-unavailable” category. Here I retain the labels for ease of discussion and because I do not include any empirical data on losses from plants, but I note that “control” and “availability” are not absolute, and that the terms are poor descriptions for N within autotrophs.
Because symbiotic BNF—a biotically controlled input that uses the inexhaustible pool of atmospheric dinitrogen gas—can bring large quantities of N into ecosystems when symbiotic N fixers are abundant, it should have the capacity to overcome any N limitation imposed by losses of plant-unavailable N (Vitousek and Howarth 1991). Vitousek and Field (1999) extended an earlier simulation model to include symbiotic BNF, and found that symbiotic BNF could overcome N limitation unless it was constrained by other resources or processes. More complex simulation models (Jenerette and Wu 2004; Rastetter and others 2001) have yielded similar results. Menge and others (2008) included symbiotic BNF in an analytical model of plant biomass and available N and found that the exact amount of symbiotic BNF necessary to overcome N limitation at steady-state was the amount lost from plant-unavailable N pools.
All of these ecosystem models were developed to address certain questions and issues—not necessarily those discussed here—so they exclude a number of issues pertinent to the current study. Most of these models use at most a single detritus pool with a single turnover time, but detailed empirical and modeling studies show that decomposition of litter alone is best described by three pools with different turnover times (Adair and others 2008), to say nothing of additional detrital pools. Although some models cited above incorporate BNF by plant–microbe symbioses, they do not include BNF by other N fixers such as lichens, cyanobacteria in bryophyte mats, or free-living heterotrophs. Plant–microbe symbioses can fix tens to hundreds of kg N ha−1 y−1 when abundant (Cleveland and others 1999), but they are rare or absent from many ecosystems (Menge and others 2010; Vitousek and Howarth 1991). On the other hand, other N fixers are ubiquitous and often important N sources, accounting for ones to occasionally tens of kg N ha−1 y−1 (for example, Antoine 2004; Cleveland and others 1999; DeLuca and others 2008; Matzek and Vitousek 2003; Menge and Hedin 2009; Reed and others 2008).
In addition to omitting some key ecosystem features that are relevant to understanding N limitation, most of the models cited above are mathematically specific. Simulation models require parameter values and specific functional forms for each process, and most analytical models also specify functional forms. The insights about biotic control over inputs and losses have greatly facilitated our understanding of N limitation, but the utility of these insights depends on their generality. For example, if the insights depend on whether plant N uptake is described by a Type I (proportional) versus a Type II (saturating, for example, Michaelis–Menten) functional response, they are less generally applicable than if both functional responses produce the same results.
In this study I investigate the generality of insights about plant-controllable versus uncontrollable inputs and losses in light of some known ecosystem complexities. Using a model with generalized functional forms for most processes, many different types of N fixers, and multiple soil organic N pools, I ask the following question: What are the conditions under which N limitation can be maintained at equilibrium? To find conditions under which N limitation can be maintained, I follow a similar approach to previous models (Menge and others 2008, 2009b; Vitousek and others 1998). First, I specify a general class of models that assumes N limitation to NPP and a few other details such as “N uptake increases with available N.” Resources aside from N—such as phosphorus, water, light, and space—and other potentially limiting factors such as herbivory or disease are not included in the model. This omission does not imply that these other factors are unimportant; indeed, there is a large body of literature demonstrating the importance of each for many questions. Rather, the focus on N alone is meant to isolate conditions that could produce sustained N limitation, a puzzling phenomenon that has received substantial attention (Jenerette and Wu 2004; Menge and others 2008; Rastetter and others 2001; Vitousek and Field 1999; Vitousek and Howarth 1991).
To analyze the model I assume that plants can become established in an ecosystem without any facilitation and that after they become established, the amounts of N in plants, other N fixers, and soils will eventually equilibrate (common dynamics in myriad specific ecosystem models). I then derive conditions—call them X—that must be true if these assumptions are met. Because they lead to equilibration, conditions X can constrain N accumulation and thus perpetuate N limitation.
After deriving these conditions I use data from a number of well-studied temperate and tropical forests that are at or near equilibrium (here I use “equilibrium” as a synonym for “steady-state”) to test the model and make predictions about whether the forests can be N-limited. If the data satisfy conditions X, they are consistent with the assumptions I made in constructing and analyzing the model, and thus consistent with N limitation. It is important to note that they do not guarantee N limitation because X may also be consistent with other models assuming that NPP is limited by other factors. However, if the data disagree with X, at least one of the assumptions I made in constructing the model must be wrong. Because I chose forests at or near equilibrium of the N cycle, the assumption most likely to be wrong is N limitation, so I interpret data that disagree with X to mean that the forests cannot be N-limited. This study builds on previous work in this area by generalizing ecosystem theory to a much broader set of conditions and offering a preliminary test of the theory with data from well-established field sites.
Methods
Model Description
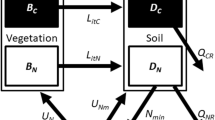
The model framework includes potentially N-fixing plants (B for biomass), heterotrophic N fixers (H), autotrophic N fixers such as cyanobacteria living in lichens and bryophytes (C for ‘cyanobacteria,’ which I will hereafter use as shorthand for these pools), an arbitrary number (m) of plant-unavailable N pools in the soil (D i for ‘detritus’), and plant-available N (A). All variables are in units of [mass N area−1]. Within-system fluxes of the model include turnover of biotic N, decomposition and mineralization of detrital N, and plant uptake of available N, but it is not necessary to specify mathematical forms for most of these fluxes.
There are abiotic inputs of plant-available N forms (I) such as wet and dry deposition that do not depend on any variable in the system, and thus are not under biotic control. I consider losses of plant-available N (k(A)) from the rooting zone—such as denitrification or leaching of nitrate, ammonium, or small organic N—“controllable” because they come from a pool plants can access. I assume that there are no losses when there is no available N (k(0) = 0) and that losses increase monotonically as available N increases (dk(A)/dA > 0). The increase could be linear, saturating (for example, Michaelis–Menten), sigmoidal (for example, logistic), or any other curve with a positive first derivative. Unless otherwise stated, these are the assumptions I make about all functions of single variables. An important point about “controllable” losses in this type of model is that plants never acquire all available N, so there are losses from that pool (k(A) > 0) despite plant control. I consider losses from plants (φ B B, where φ B is a constant rather than a function), heterotrophic N fixers (φ H (H)), cyanobacteria (φ C (C)), and all plant-unavailable soil N pools (\( \varphi_{{D_{i} }} (D_{i} ) \)) “uncontrollable” because plants cannot take up N directly from any of these pools. These losses include leaching of plant-unavailable dissolved organic N.
Finally, biotically controllable inputs are BNF from plants (BF B ), heterotrophs (F H ()), and cyanobacteria (F C ()). There is evidence that some N-fixing plants down-regulate BNF when they cease to be N-limited (for example, Barron and others 2011; Pearson and Vitousek 2001), whereas others maintain a relatively constant BNF rate per biomass despite changing soil N and other resource conditions (Binkley and others 1992; Menge and Hedin 2009). However, because the model in the current work assumes that plants are solely N-limited, they should fix at the maximum rate regardless of whether they can down-regulate BNF, so F B is a constant. Although much is known about controls on heterotrophic and cyanobacterial BNF (for example, Barron and others 2009; Benner and others 2007; Crews and others 2000; Eisele and others 1989; Silvester 1989), I need not assume anything about the arguments of the functions F H () and F C () (that is, for this analysis it does not matter whether they depend on any combination of variables or none of them) or their forms, although I do assume they cannot be negative.
Net change of total N (T) in the ecosystem is described by
where ∑φ is the sum of all losses other than k(A) (φ B B + φ H (H) + φ C (C) + \( \sum\nolimits_{i} {\varphi_{{D_{i} }} (D_{i} )} \)) and ∑F is the sum of all BNF inputs (BF B + F H () + F C ()). The change in plant N is given by
where the new terms are g(A), the N uptake function (which follows the standard assumptions listed above), μ, the turnover rate of plant N, which transfers N into one or more detritus pools, and q, a proportionality constant. The parameter q is typically 1 in models examining mechanistic nutrient-limited plant growth (DeAngelis 1992; Tilman 1982) because uptake, fixation, turnover, and loss are likely to be close to proportional to plant biomass (or in this case, plant biomass N). However, because some processes might be proportional to plant surface area rather than biomass (in which case q = 2/3) (Rastetter and Shaver 1992), I include q and allow it to be any real number. Notably, however, I do restrict this model to cases where 1/B q dB/dt (that is, the term in parentheses in equation (2)) is independent of B. Doing otherwise would implicitly introduce limitations other than nitrogen, and I am interested in understanding when limitation by nitrogen alone can be maintained. Rastetter and Agren (2002) have argued that changes in allometry should make 1/B q dB/dt depend on B, but this implicitly introduces limitations other than N (allometric changes typically stem from constraints associated with resource acquisition, such as building structural wood to compete for light). Furthermore, allometric effects are less of an issue when the accounting is done with biomass N rather than biomass due to the small concentrations of N in wood.
The change in available N is given by
where the arguments and mathematical form of net mineralization (M()) and uptake of available N by other N fixers (U()) need not be specified. These three equations are all that need be specified for the analyses in this work. Other equations describing the flow of nitrogen through plant-unavailable soil pools (D i ) or other N fixers (C or H) could be specified, but including them here would lose generality.
In reality each of these processes likely includes pulses and seasonal variation, which may be important for vegetation dynamics (Scheffer and others 2008). As in many simplified modeling studies, I make the assumption that these stochastic processes average across time and space and only examine mean-field dynamics.
Empirical Forest Data Used to Evaluate the Model
To test the predictions of this model it would be necessary to find data from old growth terrestrial ecosystems (that is, with the N cycle at or near steady-state) that had been fertilized with N and in which all N inputs and losses had been measured. To my knowledge there are few sites that fit all these criteria, so I also included sites that meet subsets of these criteria. The sites I included are montane tropical rainforests on the Long-term Substrate Age Gradient (LSAG) (Vitousek 2004) and the Maui rainfall gradient (Schuur and Matson 2001) in Hawai’i, conifer-dominated temperate forests (without alders) in the Wind River and Cascade Head Experimental Forests in Washington and Oregon (Binkley and others 1992), and montane temperate rainforests in Parque Nacional Chiloé, Chile (Hedin and others 1995) (Appendix A in Supplemental Material). Some sites in these areas such as the young Hawaiian sites are excluded because they are far from steady-state.
Atmospheric N deposition and BNF measurements likely capture the majority of N inputs to these forests, although not all potential BNF sources were measured at each site. Except for Wind River and Cascade Head, fire is unlikely to be an important N loss vector at these sites, so hydrologic and gaseous N losses from the soil likely capture most N losses. All major inputs and losses except fire are represented in at least some sites (Appendix A in Supplemental Material), so these measurements should give decent estimates of the possibility of N limitation given the model assumptions.
In many cases there are single or aggregated measures of the fluxes in these sites, but the exceptions are worth noting. At Wind River a local measurement suggested abiotic inputs of about 6.1 kg N ha−1 y−1 but nearby measurements are 2.0–2.5 kg N ha−1 y−1 (Klopatek and others 2006), so I use high (6.1) and low (2.0) estimates. To my knowledge there are no N deposition data from Cascade Head, so I used the regional estimate from a nation-wide map (Holland and others 2004). For some Maui sites two different approaches have been used to measure N gas losses. Houlton and others (2006) used isotopic measurements whereas Holtgrieve and others (2006) directly measured gas losses. I present both datasets, with Houlton’s estimates of gas to hydrologic N loss ratios for both. I also present two different estimates of abiotic N inputs on the Maui sites. The data in Houlton and others (2006) yield bulk deposition fluxes around 2 kg N ha−1 y−1, but estimates of nearby Hawaiian forests suggest that including cloud N inputs may more than triple abiotic N inputs (Carrillo and others 2002; Vitousek 2004), so I present low (2) and high (6) estimates. Hydrologic N losses are from streams except at the LSAG sites, where only lysimeter measures are available (Hedin and others 2003), and Chiloé, where both lysimeter and stream estimates are available (Perakis and others 2005; Perakis and Hedin 2002). More site and methods details are in Appendix A (Supplemental Material).
In the model soil N is divided into plant-available (A) and unavailable (D 1, …, D m ) forms, which poses a minor problem for linking with data. It is generally agreed that inorganic N forms such as nitrate and ammonium are plant-available, whereas many forms of organic N such as complex molecules of humus or lignin are not. However, some organic N molecules such as amino acids are directly plant-available (for example, Näsholm and others 1998), that is, plants can acquire and use them before mineralization (Schimel and Bennett 2004). Unfortunately, to my knowledge no studies have distinguished organic N losses that are directly plant-available from those that are not. For lack of a way to divide organic N data into available and unavailable, here I initially assume that all organic N is plant-unavailable, which might underestimate plant-available N and overestimate plant-unavailable N. To examine the sensitivity of this assumption I then derive the percentages of organic N in losses that would need to be plant-available to qualitatively change the results for each site.
Results
Model Analysis
For an N-limited equilibrium to exist, N inputs must equal N losses under the assumption of N limitation. If “*” denotes an equilibrium value of a variable (for A) or flux (for F and φ, which depend on variables), the statement that inputs equal losses from equation (1) can be rearranged to
In many ecosystems primary succession begins with N fixers like lichens, and plants invade later. Although other N fixers might facilitate plant growth, I assume that plants do not require facilitation to become established because abiotic inputs will eventually supply enough N for non-fixing plants to establish. Although current evidence does not suggest that facilitation by other N fixers is obligatory for primary succession (Walker and del Moral 2003), and I think the assumption is reasonable, it is difficult to evaluate empirically due to the ubiquity of N-fixing microbes. In the example models I have examined, assuming that facilitation is required for plant establishment leads to an unstable system that either crashes or grows without bound, and thus is unrealistic. I show the implications of requiring facilitation in Supplemental Material Appendix B (Supplemental Material).
The assumption that plants can become established without facilitation means that the growth rate (dB/dt from equation (2)) of a very small population—say a small individual—is positive when no other plants, cyanobacteria, heterotrophic N fixers, or detritus are present. The equilibrium amount of available N in an ecosystem with no plants, other N fixers, or detritus, which I denote A 0, is defined by the relationship
A very small plant population has a negligible effect on the amount of available N, so the amount of available N immediately after the introduction of a very small population is still approximately A 0. Therefore, the assumption that plants can establish (dB/dt evaluated for very small B > 0) is equivalent to
Assuming that plants can establish in the empty equilibrium does not necessarily mean that the ecosystem had to be at the empty equilibrium before plants were introduced—only that they could establish at the empty equilibrium if they could not before. From setting equation (2) equal to zero, the equilibrium of A when plants are present (A*) is defined by
From conditions 6 and 7, g(A 0) > g(A*). The function g(A) increases monotonically, so
This makes sense from the perspective of standard plant-resource models (for example, Tilman 1982). If plants can survive in an ecosystem and are limited by a resource, they will eventually draw that resource down to a lower level than it had reached without plants.
Because k(A) is also monotonically increasing, and because of conditions 5 and 8,
Biologically, this means that if plants do not require facilitation to become established, N limitation at equilibrium is only possible if abiotic inputs exceed losses from plant-available N pools. Continuing this reasoning, equation (4) and condition 9 show that an N-limited equilibrium is only possible when biotically uncontrollable losses exceed all BNF inputs:
What happens when condition 9 or 10 is violated, that is, when losses from plant-available N pools exceed abiotic inputs or BNF inputs exceed losses from plant-unavailable N pools? In a real ecosystem at or near equilibrium, a measurement of losses from plant-available N pools exceeding abiotic inputs or a measurement of BNF exceeding losses of plant-unavailable N would indicate that at least one assumption in this model is wrong. Provided that facilitation is not needed, the assumption most likely to be incorrect is N limitation, in which case a measurement of k(A*) > I or ∑F* > ∑φ* would indicate that the ecosystem cannot be solely N-limited.
In the model, an N-limited equilibrium is impossible when condition 9 or 10 is violated, as the following contradiction proves. At equilibrium, if ∑F* ≥ ∑φ*, then from equation (4), k(A*) ≥ I. If k(A*) ≥ I = k(A 0), then A* ≥ A 0 , so g(A*) ≥ g(A 0). If g(A*) ≥ g(A 0), then assuming plants can establish in the empty ecosystem (condition 6), g(A*) > \(\mu_{B} + \varphi_{B} - F_{B}\). However, the equilibrium value A* is defined by g(A*) = μ B + φ B − F B (equation (7)), and g(A*) cannot be greater than itself, revealing the contradiction. In fact, when plant-available N remains at or above its base level (A ≥ A 0), as implied by a measurement of k(A*) > I, plants in the model grow without bound (g(A) ≥ g(A 0) > \(\mu_{B} + \varphi_{B} - F_{B}\); dB/dt > 0). Perpetual growth is impossible in reality, so this model result suggests that N cannot constrain plant growth when k(A*) ≥ I or ∑F* ≥ ∑φ*.
Successional Changes in Species and Parameters
This analysis concerns late-successional (equilibrium) conditions, yet makes the assumption that late-successional plants could invade a plant-less environment given sufficient time and lack of competition from early-successional plants. This is not quite the same as assuming that late-successional plants could invade an early-successional environment, because the “plant-less environment” is set by parameters (loss rates and atmospheric deposition fluxes) measured during late succession. Even so, it is difficult to evaluate this assumption in nature because early-successional plants would colonize such environments before late-successional plants. Hence, it is useful to ask whether these assumptions can be derived from more defensible assumptions. Using different subscripts for parameter values measured when plants are absent (“0”), when early-successional plants are present (“early”), and when late-successional plants are present (“late”), I now ask whether more standard assumptions lead to the same conclusion that late-successional plants could invade a plant-less, late-successional environment, that is, that I late > k late(\( A_{\text{late}}^{*} \)).
Almost by definition, early-successional plants can invade early-successional environments and late-successional plants can out-compete early-successional plants. From the same logic as above, early-successional plants can invade early-successional environments when I 0 > k early(\( A_{\text{early}}^{*} \)), which is equivalent to when A 0 > \( A_{\text{early}}^{*} \). In this type of model, species replacement can only happen if late-successional species survive on a lower A* than early-successional species (Tilman 1982), so assuming that late-successional plants can out-compete early-successional plants is the same as assuming that \( A_{\text{early}}^{*} \) > \( A_{\text{late}}^{*} \). Do these assumptions imply that I late > k late(\( A_{\text{late}}^{*} \))?
From the inequalities in the previous paragraph it is clear that these assumptions imply that A 0 > \( A_{\text{early}}^{*} \) > \( A_{\text{late}}^{*} \), and therefore that I = k(A 0) > k(\( A_{\text{early}}^{*} \)) > k(\( A_{\text{late}}^{*} \)) for given I and function k. However, the abiotic N input parameter I and the loss function k(A) may also change during succession. Although I know of no evidence, it is conceivable that atmospheric N deposition could increase through succession because increased surface area from plants is more likely to trap N molecules from the atmosphere, so I examine the case of I late > I early > I 0. Hydrologic losses per unit N molecule might decrease through succession because soils are increasingly deep and clayey, which would mean that k 0(A) > k early(A) > k late(A) for a given A. Conversely, denitrification losses per unit N molecule might increase through succession because of the increase in organic matter and the increased proportion of anaerobic sites. If the successional change in hydrologic N losses outweighs the change in denitrification or they are similar,
which would guarantee that I late > k late(\( A_{\text{late}}^{*} \)). Even if the successional change in denitrification is larger than the change in hydrologic N losses, it is still likely that the other inequalities in I and A* outweigh it. So, the initial assumption and therefore the main results can be derived directly from the assumptions that early-successional plants can establish in early-successional habitats, late-successional plants can out-compete early-successional plants, abiotic N inputs do not decrease through succession, and the loss strength of available N decreases or does not increase much through succession. Even though other parameters and functions aside from I and k(A) might change through succession, they would not affect this conclusion except through effects of g(A), μ B , φ B , and F B on A*, which are already covered under the assumptions of early-successional plants colonizing the empty habitat and late-successional plants out-competing early-successional plants.
Model Evaluation with Data
Along the Hawaiian age (LSAG) gradient, abiotic N inputs (I) exceeded losses from plant-available N pools (k(A*)) in all but the oldest site (Figure 1; gray indicates N limitation is impossible). However, losses of DON (∑φ*) exceeded BNF inputs (∑F*) at all sites, including the oldest. Total measured losses exceeded inputs by 4.2 kg N ha−1 y−1 at the oldest site, accounting for the discrepancy. In temperate forests at Wind River and Chiloé, I exceeded k(A*) and ∑φ* exceeded ∑F* for all combinations of high and low estimates (Figure 1). Nitrogen losses from fire would only increase ∑φ*, so they would enhance the observed inequality in these sites. In contrast, k(A*) exceeded I by over 11 kg N ha−1 y−1 in the temperate forest at Cascade Head. Losses of DON at Cascade Head were 7.3 kg N ha−1 y−1 and including fire would increase ∑φ*, but BNF was not measured. On Maui, isotopic estimates of losses from plant-available N pools suggested that k(A*) exceeded low and high I estimates (I low and I high) except at the 2750 mm y−1 site where k(A) fell between I low and I high (Figure 1). On the contrary, direct estimates of gas losses suggested that k(A*) exceeded both I low and I high at the 2200 mm y−1 site but neither at the 3350 or 4050 mm y−1 site. Estimates of DON loss ranged from 1.1 to 7.9 kg N ha−1 y−1 for the isotopic measurements and 0.14 to 3.1 kg N ha−1 y−1 for the direct measurements. BNF was not measured for any of the Maui sites.
Model predictions about whether nitrogen (N) can limit net primary production in different forest ecosystems. According to the model, N limitation is only possible when abiotic N inputs (I, which include wet deposition, dry deposition, and cloud deposition) exceed losses originating from plant-available N pools (k(A*), which include hydrologic and gaseous losses from the nitrate and ammonium soil pools), which should be equivalent to when losses originating from plant-unavailable N pools (∑φ*, which include leaching of dissolved organic N) exceed biological N fixation (BNF) inputs (∑F*, from all types of N fixers). Gray bars indicate that k(A*) > I, implying that N limitation is not possible in these sites. Not all of these fluxes are included at each site (see Appendix A in Supplemental Material). Abiotic inputs (I) and losses from plant-available N pools (k(A*)) are on the left of each site, in black if I > k(A*) or gray if k(A*) > I. BNF inputs (∑F*) and losses from plant-unavailable N pools (∑φ*) are on the right of each site in white. Missing flux data are indicated with ‘???.’ In some cases different flux estimates are available; these are shown as split bars.
Figure 2 shows the effects of relaxing the assumption that all organic N lost from the ecosystem is unavailable to plants. If the original comparisons already suggested that N limitation is impossible, as at the LSAG 4100 ky, Cascade Head, and some Maui sites/comparisons (all based on I vs. k(A*)), increasing the magnitude of losses from plant-available N pools does not alter the prediction. For a number of other sites (LSAG 150 ky, Wind River with high I, and all other Maui sites/comparisons, all based on I vs. k(A*)), the prediction that N limitation is possible cannot be altered even if all organic N losses were in plant-available form. At all other sites, assuming that some fraction of organic N loss is from plant-available pools alters the prediction, depending on the exact fraction. For example, at the LSAG 20 ky site, if half (based on ∑F* vs. ∑φ*) to most (based on I vs. k(A*)) of organic N losses are in plant-available form, N limitation is impossible at this site. At the LSAG 1400 ky site, assuming that 3% (based on I vs. k(A*)) to about half (based on ∑F* vs. ∑φ*) of organic N losses are in plant-available form renders N limitation impossible. At Wind River, the cutoffs are 22% based on low I versus k(A*) and 37% based on ∑F* versus ∑φ*. At Chiloé the cutoffs are between 36% and 89%.
Sensitivity analyses of results in Figure 1 to organic N availability. Values presented are percents of organic N losses that would need to be in plant-available form to alter the result shown in Figure 1, for the I versus k(A*) (black) and the ∑F* versus ∑φ* comparisons (white). For example, based on the I versus k(A*) comparison at the LSAG 20 ky site, if more than 93% of the organic N being lost were in plant-available form, the model would indicate that N limitation at this site would be impossible. Cases where the results in Figure 1 indicate that N limitation is impossible cannot change and are presented as “0” values (without ‘???’). Values above the dashed line (100%) also could not change; many of these exceed 110% but the figure is truncated at 110% for ease of data presentation. Comparisons with missing fluxes are indicated with ‘???.’ Sites and scenarios are generally laid out as in Figure 1, except that at the Maui sites all combinations of high and low inputs with isotopic-based and direct measurements of losses are presented.
Discussion
Model Comparison to Data
In general, my model accurately predicted N limitation in real ecosystems. Empirical tests of nitrogen limitation—that is, fertilization studies—would invalidate the model by showing N limitation to NPP when (i) losses from plant-available N pools exceed abiotic N inputs or (ii) BNF inputs exceed losses from plant-unavailable N pools. Among the sites included in this study, only the 20 and 4100 ky Hawaiian LSAG sites have been fertilized. The 20 ky site is co-limited by N and P, whereas the 4100 ky site is limited by P alone (Vitousek and Farrington 1997). These results match the model predictions, which are that the 20 ky site can be N-limited unless a majority of organic N losses are in plant-available form but the 4100 ky site cannot, regardless of organic N availability.
To my knowledge there have been no measurements of the proportion of organic N in hydrologic losses that is in plant-available form. However, the proportion in hydrologic losses is likely to be similar to the proportion in soil solution, which is thought to be small, corresponding to rapid turnover rates of amino acids (Schimel and Bennett 2004). A recent analysis of N forms dissolved in soil solution below four different soil types in Sweden found that free amino acids were 50 times less abundant than amino acids bound in dissolved proteins (Jämtgård and others 2010). If the proportion of plant-available organic N is similarly small (2%, or even less than 10%) in hydrologic losses, the only model prediction that might change would be that the 1400 ky LSAG site could not be N-limited, which would still match with the speculation that this site is P limited (Parton and others 2005; Vitousek 2004). Studies elucidating the availability of organic N in hydrologic losses and other media are much needed.
Other models have also reproduced the observed patterns of nutrient limitation along the LSAG sites (Parton and others 2005; Wang and others 2007), and do so in a far more comprehensive way than does the present work, predicting quantitative pools and fluxes as well as nutrient limitation. However, these more complex models require well-constrained information on a multitude of parameters, whereas the simple framework in the present work requires fairly crude knowledge of only a few fluxes.
Researchers working on some of the other forests included in Figure 1 have speculated about their limitation status, although the forests have not been fertilized. Wind River (Binkley and others 1992) and Chiloé (Hedin and others 1995) are thought to be N-limited. These speculations agree with my model predictions as long as the proportions of organic N losses that are in plant-available form are not large. Cascade Head is thought not to be N-limited (Binkley and others 1992), matching the prediction of my model. Measurements of BNF at Cascade Head, which would be near 20 kg N ha−1 y−1 if the N cycle is near equilibrium, would further elucidate N cycle dynamics.
The Maui sites highlight the importance of accurate N flux measurements because different estimates yield conflicting results. All estimates of abiotic inputs and losses from plant-available N pools suggest that the 2200 and 2450 mm Maui sites cannot be N-limited, whereas for the wetter sites the possibility of N limitation is unclear. There are some suggestions that the wettest sites are N-limited (Schuur and Matson 2001), but if losses from plant-available N pools are as high as the isotopic measurements suggest, the model or the limitation status would come into question, regardless of the form of organic N losses. Measurements of BNF at these sites would help address these issues, and are likely to yield interesting patterns in their own right. If the N cycle is near equilibrium in these forests, BNF could range from negligible at the wettest site to more than 20 kg N ha−1 y−1 at the least wet site.
Ecosystem Theory Insights
The theoretical result that equilibrium N limitation is impossible when symbiotic BNF inputs exceed losses from plant-unavailable N pools (Menge and others 2008) is robust to the generalizations tested here. Whereas Menge and others (2008) used linear forms of N uptake and loss with specific within-system N cycling, the current study shows that any monotonically increasing uptake and loss functions—such as Michaelis–Menten or logistic—and myriad combinations of within-system fluxes yield the same results. Similarly, including multiple detrital pools, as seems to be important for describing litter decomposition (Adair and others 2008), has no effect on the basic result, so more complicated models are subject to the same constraint. Whereas some previous studies included N losses from either autotrophs (DeAngelis 1992) or detritus (Menge and others 2009b; Rastetter and others 2005; Vitousek and others 1998), this model shows that all N losses from pools other than plant-available N have a similar qualitative effect on maintaining N limitation, as suggested by Vitousek and Field (1999). Additionally, the model yields similar results if there are successional changes in a variety of parameters.
This model adds new insight by showing that understanding the maintenance of N limitation requires knowledge of controls on all types of N fixers rather than just symbiotic N fixers. Because plant–microbe symbioses can fix tens to hundreds of kg N ha−1 y−1 (Binkley and others 1992; Cleveland and others 1999), which greatly exceeds typical losses from plant-unavailable N pools (Figure 1), it is clearly essential to understand what controls their abundance and activity (Vitousek and Howarth 1991), and progress has been made in this area (Jenerette and Wu 2004; Menge and others 2008, 2009a; Rastetter and others 2001; Uliassi and Ruess 2002; Vitousek and Field 1999). However, N-fixing plant–microbe symbioses are rare or absent in many ecosystems (Menge and others 2010; Vitousek and Howarth 1991), yet BNF from other N fixers such as lichens, cyanobacteria in bryophytes, free-living cyanobacteria, and heterotrophic bacteria is ubiquitous. The current work shows that BNF by these other N fixers can prevent N limitation to NPP if it exceeds losses from plant-unavailable N pools. These other N fixers often exist in N-poor biogeochemical niches within a forest (Menge and Hedin 2009; Reed and others 2008), so they often fix N even when soil N availability is high. In addition to responding to their local N availability (Barron and others 2009; Crews and others 2000; Cusack and others 2009; DeLuca and others 2007; Liengen 1999; Zackrisson and others 2004), BNF by lichens, cyanobacteria in bryophytes, and heterotrophs in leaf litter, wood, and soil has been shown to respond to temperature (Antoine 2004; Kurina and Vitousek 2001; Liengen 1999), water (Antoine 2004; Freiberg 1998; Kurina and Vitousek 2001; Vitousek 1994), light (Freiberg 1998; Kurina and Vitousek 2001; Liengen 1999; Reed and others 2008), phosphorus (Benner and others 2007; Crews and others 2000; Eisele and others 1989; Liengen 1999; Reed and others 2007a, b; Vitousek 1999), molybdenum (Barron and others 2009; Silvester 1989), and combinations of nutrients (Crews and others 2000, 2001; Vitousek 1999). Although much is known about potential controls, further studies elucidating which of these controls is important in different environments—and particularly why—would improve our understanding of ecosystem-level N limitation.
Although it is intuitive that sufficiently large BNF rates can overcome N limitation, it seems counterintuitive that sufficiently low abiotic N inputs (k(A*) > I) render N limitation impossible. For example, the model states that N cannot limit NPP at Cascade Head, where losses of plant-available N forms exceed abiotic inputs. Would increasing abiotic inputs at Cascade Head make N limitation possible? The primary explanation for this apparent paradox is that large losses from plant-available N pools indicate a relaxation of plant control on available N in the soil (Vitousek and Reiners 1975). When purely N-limited plants can inhabit an ecosystem without any facilitation from other N fixers, they draw down available N as they grow, which yields lower losses from plant-available N pools. On the contrary, when N does not limit NPP, plants do not absorb excess N, so increases in I would be matched by increases in k(A*) to maintain steady-state (I would not exceed k(A*)). A secondary explanation concerns the model assumption of N limitation: it shows when N limitation is possible rather than when it is expected because no other resources are included in the model. Increasing abiotic N inputs in real forests eventually saturates N demand (Aber and others 1989), and the model would reflect this if other potentially limiting resources were included.
The steady-state conditions that form the main results of this paper are indicators of whether N can limit NPP, but because the N cycle is a cycle, the causal links go both ways. For example, low losses of plant-available N result from plants depleting available N levels, but low available N levels are what cause N limitation in the first place.
Applying this Theory to Real Ecosystems
Practically, the result that k(A*) > I renders N limitation impossible could offer a crude but rapid diagnosis of whether old-growth forests can be N-limited. The conditions under which this model applies—chiefly, a steady-state N cycle—restrict its applicability, but using k(A*) versus I rather than ∑F* versus ∑φ* is much less restrictive. Available N in the soil (A) approaches its long-term equilibrium on the timescale of plant biomass N (seen from equation (2)), which is typically much sooner (decades to centuries) than the entire ecosystem (millennia or longer) (Menge and others 2009b). This means that comparing losses of plant-available N to abiotic N inputs measured at any time beginning when plant biomass N (rather than the entire N cycle) is near equilibrium indicates what the equilibrium relationship will be. On the contrary, comparing measurements of BNF and losses of plant-unavailable N only indicates the equilibrium relationship when the entire N cycle is at equilibrium because plant-unavailable soil N pools are typically the last ecosystem component to equilibrate (Menge and others 2009b). In addition to being more applicable, comparing k(A*) to I is also likely to be more accurate than comparing ∑F* and ∑φ* given the relatively greater ease of measuring these fluxes. However, none of these fluxes is easy to measure, and the difficulties associated with these measurements—such as determining which N forms are plant-available—can make it hard to use these results operationally. Large losses of plant-available N forms are already used to infer N saturation or N richness in many real ecosystems (for example, Aber and others 1989; Hedin and others 2009), though, and in that sense the current work puts a threshold on what constitutes “large” losses—greater than abiotic inputs. Because abiotic deposition maps are widely available (for example, Holland and others 2004), this work could provide theoretical guidance to a practice already in use.
One benefit of this method is that it does not depend on a full accounting of losses of plant-unavailable N. Gas losses such as denitrification can be difficult to quantify accurately (Groffman and others 2006), and as discussed above, partitioning organic N into plant-available versus plant-unavailable forms is similarly tricky. Hydrologic losses of inorganic N (leaching of ammonium and nitrate), though, are relatively easy to measure, and it is possible to make headway with these alone. A measurement of ammonium and nitrate leaching exceeding N deposition in a forest near steady-state implies a lack of N limitation to NPP. Even if ammonium and nitrate leaching comprised all losses of plant-available N, the opposite result—N deposition exceeding ammonium and nitrate leaching—would not imply N limitation because other potentially limiting resources and factors are not included in the model.
More extensive empirical testing of this theory is necessary, and of course the biogeochemical details of individual ecosystems need to be considered (for example, weathering of bedrock with significant N would need to be included in I), but it might be feasible to use this technique as a rapid diagnosis of whether a steady-state ecosystem can be N-limited. This information, in turn, can help understand broader issues of CO2 uptake, eutrophication from nitrate leaching, and N2O emissions that contribute to greenhouse warming, because these issues hinge on whether N limits NPP.
The present work applies to ecosystems in which the N cycle is at or near equilibrium, that is, old-growth forests. Although the mathematics are likely to be less elegant, similar results likely hold for systems farther from equilibrium, and future work in this area could help extend these insights to a larger portion of the globe. Additionally, future work examining some of the other assumptions I make here would help pin down controls on N limitation. An important example is the assumption in the current work of sole limitation by N. Co-limitation is thought to be common (Bloom and others 1985), and some models that incorporate co-limitation with a non-recycled resource such as light allow for stable equilibria even when plant-controlled nutrient inputs exceed uncontrolled nutrient losses (for example, Ju and DeAngelis 2010).
References
Aber JA, Nadelhoffer KJ, Steudler P, Melillo JM. 1989. Nitrogen saturation in Northern forest ecosystems. Bioscience 39:378–86.
Adair EC, Parton WJ, Del Grosso SJ, Silver WL, Harmon ME, Hall SA, Burke IC, Hart SC. 2008. Simple three-pool model accurately describes patterns of long-term litter decomposition in diverse climates. Glob Change Biol 14(11):2636–60.
Antoine ME. 2004. An ecophysiological approach to quantifying nitrogen fixation by Lobaria oregana. Bryologist 107(1):82–7.
Barron AR, Wurzburger N, Bellenger JP, Wright SJ, Kraepiel AML, Hedin LO. 2009. Molybdenum limitation of asymbiotic nitrogen fixation in tropical forest soils. Nat Geosci 2(1):42–5.
Barron AR, Purves DW, Hedin LO. 2011. Facultative nitrogen fixation by canopy legumes in a lowland tropical forest. Oecologia 165(2):511–20.
Benner JW, Conroy S, Lunch CK, Toyoda N, Vitousek PM. 2007. Phosphorus fertilization increases the abundance and nitrogenase activity of the cyanolichen Pseudocyphellaria crocata in Hawaiian montane forests. Biotropica 39(3):400–5.
Binkley D, Sollins P, Bell R, Sachs D, Myrold D. 1992. Biogeochemistry of adjacent conifer and alder-conifer stands. Ecology 73(6):2022–33.
Bloom AJ, Chapin FSI, Mooney HA. 1985. Resource limitation in plants: an economic analogy. Annu Rev Ecol Syst 21:363–92.
Carrillo JH, Hastings MG, Sigman DM, Huebert BJ. 2002. Atmospheric deposition of inorganic and organic nitrogen and base cations in Hawaii. Global Biogeochem Cycles 16(4):1076. doi:10.1029/2002GB001892.
Cleveland CC, Townsend AR, Schimel DS, Fisher H, Howarth RW, Hedin LO, Perakis SS, Latty EF, Von Fischer JC, Elseroad A et al. 1999. Global patterns of terrestrial biological nitrogen (N-2) fixation in natural ecosystems. Global Biogeochem Cycles 13(2):623–45.
Crews TE, Farrington H, Vitousek PM. 2000. Changes in asymbiotic, heterotrophic nitrogen fixation on leaf litter of Metrosideros polymorpha with long-term ecosystem development in Hawaii. Ecosystems 3:386–95.
Crews TE, Kurina LM, Vitousek PM. 2001. Organic matter and nitrogen accumulation and nitrogen fixation during early ecosystem development in Hawaii. Biogeochemistry 52:259–79.
Currie WS, Aber JD, McDowell WH, Boone RD, Magill AH. 1996. Vertical transport of dissolved organic C and N under long-term N amendments in pine and hardwood forests. Biogeochemistry 35(3):471–505.
Cusack DF, Silver W, McDowell WH. 2009. Biological nitrogen fixation in two tropical forests: ecosystem-level patterns and effects of nitrogen fertilization. Ecosystems 12(8):1299–315.
DeAngelis DL. 1992. Dynamics of nutrient cycling and food webs. London: Chapman and Hall.
DeLuca TH, Zackrisson O, Gentili F, Sellstedt A, Nilsson MC. 2007. Ecosystem controls on nitrogen fixation in boreal feather moss communities. Oecologia 152(1):121–30.
DeLuca TH, Zackrisson O, Gundale MJ, Nilsson MC. 2008. Ecosystem feedbacks and nitrogen fixation in boreal forests. Science 320(5880):1181.
Eisele KA, Schimel DS, Kapustka LA, Parton WJ. 1989. Effects of available P-ratio and N-P-ratio on non-symbiotic dinitrogen fixation in tallgrass prairie soils. Oecologia 79(4):471–4.
Freiberg E. 1998. Microclimatic parameters influencing nitrogen fixation in the phyllosphere in a Costa Rican premontane rain forest. Oecologia 17:9–18.
Galloway JN, Dentener FJ, Capone DG, Boyer EW, Howarth RW, Seitzinger SP, Asner GP, Cleveland CC, Green PA, Holland EA et al. 2004. Nitrogen cycles: past, present, and future. Biogeochemistry 70(2):153–226.
Groffman PM, Altabet MA, Bohlke JK, Butterbach-Bahl K, David MB, Firestone MK, Giblin AE, Kana TM, Nielsen LP, Voytek MA. 2006. Methods for measuring denitrification: diverse approaches to a difficult problem. Ecol Appl 16(6):2091–122.
Hall SJ, Matson PA. 1999. Nitrogen oxide emissions after nitrogen additions in tropical forests. Nature 400(6740):152–5.
Hall SJ, Matson PA. 2003. Nutrient status of tropical rain forests influences soil N dynamics after N additions. Ecol Monogr 73(1):107–29.
Hedin LO, Armesto JJ, Johnson AH. 1995. Patterns of nutrient loss from unpolluted, old-growth temperate forests: evaluation of biogeochemical theory. Ecology 76:493–509.
Hedin LO, Vitousek PM, Matson PA. 2003. Nutrient losses over four million years of tropical forest development. Ecology 84(9):2231–55.
Hedin LO, Brookshire ENJ, Menge DNL, Barron AR. 2009. The nitrogen paradox in tropical forest ecosystems. Annu Rev Ecol Evol Syst 40:613–35.
Holland EA, Braswell GH, Sulzman J, Lamarque J-F. 2004. Nitrogen deposition onto the United States and Western Europe. Data set. Available online [http://www.daac.ornl.gov] from the Oak Ridge National Laboratory Distributed Archive Center. Oak Ridge, Tennessee, USA.
Holloway JM, Dahlgren RA. 2002. Nitrogen in rock: occurrences and biogeochemical implications. Global Biogeochem Cycles 16(4):65-1–17.
Holtgrieve GW, Jewett PK, Matson PA. 2006. Variations in soil N cycling and trace gas emissions in wet tropical forests. Oecologia 146(4):584–94.
Houlton BZ, Sigman DM, Hedin LO. 2006. Isotopic evidence for large gaseous nitrogen losses from tropical rainforests. Proc Natl Acad Sci USA 103(23):8745–50.
Jämtgård S, Näsholm T, Huss-Danell K. 2010. Nitrogen compounds in soil solutions of agricultural land. Soil Biol Biochem 42(12):2325–30.
Jenerette GD, Wu J. 2004. Interactions of ecosystem processes with spatial heterogeneity in the puzzle of nitrogen limitation. Oikos 107:273–82.
Ju S, DeAngelis DL. 2010. Nutrient fluxes at the landscape level and the R* rule. Ecol Model 221(2):141–6.
Klopatek JM, Barry MJ, Johnson DW. 2006. Potential canopy interception of nitrogen in the Pacific Northwest, USA. For Ecol Manag 234(1–3):344–54.
Kurina LM, Vitousek PM. 2001. Nitrogen fixation rates of Stereocaulon vulcani on young Hawaiian lava flows. Biogeochemistry 55(2):179–94.
LeBauer DS, Treseder KK. 2008. Nitrogen limitation of net primary productivity in terrestrial ecosystems is globally distributed. Ecology 89(2):371–9.
Liengen T. 1999. Environmental factors influencing the nitrogen fixation activity of free-living terrestrial cyanobacteria from a high arctic area, Spitsbergen. Can J Microbiol 45(7):573–81.
Matzek V, Vitousek PM. 2003. Nitrogen fixation in bryophytes, lichens, and decaying wood along a soil-age gradient in Hawaiian montane rain forest. Biotropica 35(1):12–19.
Menge DNL, Hedin LO. 2009. Nitrogen fixation in different biogeochemical niches along a 120,000-year chronosequence in New Zealand. Ecology 90(8):2190–201.
Menge DNL, Levin SA, Hedin LO. 2008. Evolutionary tradeoffs can select against nitrogen fixation and thereby maintain nitrogen limitation. Proc Natl Acad Sci USA 105(5):1573–8.
Menge DNL, Levin SA, Hedin LO. 2009a. Facultative versus obligate nitrogen fixation strategies and their ecosystem consequences. Am Nat 174(4):465–77.
Menge DNL, Pacala SW, Hedin LO. 2009b. Emergence and maintenance of nutrient limitation over multiple timescales in terrestrial ecosystems. Am Nat 173(2):164–75.
Menge DNL, DeNoyer JL, Lichstein JW. 2010. Phylogenetic constraints do not explain the rarity of nitrogen-fixing trees in late-successional temperate forests. PLoS ONE 5(8):e12056.
Näsholm T, Ekblad A, Nordin A, Giesler R, Högberg M, Högberg P. 1998. Boreal forest plants take up organic nitrogen. Nature 392:914–16.
Parton WJ, Neff J, Vitousek PM. 2005. Modelling phosphorus, carbon, and nitrogen dynamics in terrestrial ecosystems. In: Turner BL, Frossard E, Baldwin DS, Eds. Organic phosphorus in the environment. Cambridge: CABI. p 325–48.
Pearson HL, Vitousek PM. 2001. Stand dynamics, nitrogen accumulation, and symbiotic nitrogen fixation in regenerating stands of Acacia koa. Ecol Appl 11(5):1381–94.
Perakis SS, Hedin LO. 2002. Nitrogen loss from unpolluted South American forests mainly via dissolved organic compounds. Nature 415(6870):416–19.
Perakis SS, Compton JE, Hedin LO. 2005. Nitrogen retention across a gradient of 15 N additions to an unpolluted temperate forest soil in Chile. Ecology 86(1):96–105.
Pérez CA, Carmona MR, Armesto JJ. 2003. Non-symbiotic nitrogen fixation, net nitrogen mineralization and denitrification in evergreen forests of Chiloé island, Chile: a comparison with other temperate forests. Gayana Botánica 60(1):25–33.
Rastetter EB, Agren GI. 2002. Changes in individual allometry can lead to species coexistence without niche separation. Ecosystems 5(8):789–801.
Rastetter EB, Shaver GR. 1992. A model of multiple-element limitation for acclimating vegetation. Ecology 73(4):1157–74.
Rastetter EB, Vitousek PM, Field CB, Shaver GR, Herbert DA, Agren GI. 2001. Resource optimization and symbiotic nitrogen fixation. Ecosystems 4:369–88.
Rastetter EB, Perakis SS, Shaver GR, Agren GI. 2005. Terrestrial C sequestration at elevated-CO2 and temperature: the role of dissolved organic N loss. Ecol Appl 15(1):71–86.
Reed SC, Cleveland CC, Townsend AR. 2007a. Controls over leaf litter and soil nitrogen fixation in two lowland tropical rain forests. Biotropica 39(5):585–92.
Reed SC, Seastedt TR, Mann CM, Suding KN, Townsend AR, Cherwin KL. 2007b. Phosphorus fertilization stimulates nitrogen fixation and increases inorganic nitrogen concentrations in a restored prairie. Appl Soil Ecol 36(2–3):238–42.
Reed SC, Cleveland CC, Townsend AR. 2008. Tree species control rates of free-living nitrogen fixation in a tropical rain forest. Ecology 89(10):2924–34.
Scheffer M, van Nes EH, Holmgren M, Hughes T. 2008. Pulse-driven loss of top-down control: the critical-rate hypothesis. Ecosystems 11(2):226–37.
Schimel JP, Bennett J. 2004. Nitrogen mineralization: challenges of a changing paradigm. Ecology 85(3):591–602.
Schuur EAG, Matson PA. 2001. Net primary productivity and nutrient cycling across a mesic to wet precipitation gradient in Hawaiian montane forest. Oecologia 128(3):431–42.
Silvester WB. 1989. Molybdenum limitation of asymbiotic nitrogen fixation in forests of Pacific Northwest America. Soil Biol Biochem 21:283–9.
Sollins P, Grier CC, McCorison FM, Cromack K, Fogel R. 1980. The internal element cycles of an old-growth douglas-fir ecosystem in western Oregon. Ecol Monogr 50(3):261–85.
Tilman D. 1982. Resource competition and community structure. Princeton, NJ: Princeton University Press. p 296.
Uliassi DD, Ruess RW. 2002. Limitations to symbiotic nitrogen fixation in primary succession on the Tanana River floodplain. Ecology 83(1):88–103.
Vitousek PM. 1994. Potential nitrogen fixation during primary succession in Hawaii Volcanoes National Park. Biotropica 26:234–40.
Vitousek PM. 1999. Nutrient limitation to nitrogen fixation in young volcanic sites. Ecosystems 2:505–10.
Vitousek PM. 2004. Nutrient cycling and limitation: Hawai’i as a model system. Princeton, NJ: Princeton University Press.
Vitousek PM, Farrington H. 1997. Nutrient limitation and soil development: experimental test of a biogeochemical theory. Biogeochemistry 37:63–75.
Vitousek PM, Field CB. 1999. Ecosystem constraints to symbiotic nitrogen fixers: a simple model and its implications. Biogeochemistry 46:179–202.
Vitousek PM, Howarth RW. 1991. Nitrogen limitation on land and in the sea: how can it occur? Biogeochemistry 13:87–115.
Vitousek PM, Reiners WA. 1975. Ecosystem succession and nutrient retention—hypothesis. Bioscience 25(6):376–81.
Vitousek PM, Hedin LO, Matson PA, Fownes JH, Neff J. 1998. Within-system element cycles, input-output budgets, and nutrient limitation. In: Pace ML, Groffman PM, Eds. Successes, limitations, and frontiers in ecosystem science. New York: Springer. p 432–51.
Walker LR, del Moral R. 2003. Primary succession and ecosystem rehabilitation. New York, NY: Cambridge University Press.
Wang YP, Houlton BZ, Field CB. 2007. A model of biogeochemical cycles of carbon, nitrogen, and phosphorus including symbiotic nitrogen fixation and phosphatase production. Global Biogeochem Cycles 21:GB1018. doi:10.1029/2006GB002797.
Weathers KC, Lovett GM, Likens GE, Caraco NFM. 2000. Cloudwater inputs of nitrogen to forest ecosystems in southern Chile: forms, fluxes, and sources. Ecosystems 3(6):590–5.
Zackrisson O, DeLuca TH, Nilsson M-C, Sellstedt A, Berglund LM. 2004. Nitrogen fixation increases with successional age in boreal forests. Ecology 85(12):3327–34.
Acknowledgments
J. Balch, F. Ballantyne, J. Brookshire, S. Levin, E. Rastetter, L. Wolkovich, and two anonymous reviewers provided valuable comments on earlier drafts. The author was supported in part as a Postdoc at the National Center for Ecological Analysis and Synthesis, a Center funded by the NSF (Grant #EF-0553768), the University of California, Santa Barbara, and the State of California, and in part by the Carbon Mitigation Initiative, with funding from BP and Ford.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Author Contributions
DNLM conceived of and designed the study, performed the research, analyzed the data, contributed new models, and wrote the paper.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Menge, D.N.L. Conditions Under Which Nitrogen Can Limit Steady-State Net Primary Production in a General Class of Ecosystem Models. Ecosystems 14, 519–532 (2011). https://doi.org/10.1007/s10021-011-9426-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10021-011-9426-x