Skip to main content
SpringerLink
Log in

Kruskal-Katona type theorems for clique complexes arising from chordal and strongly chordal graphs

  • Published:
Combinatorica Aims and scope Submit manuscript

Abstract

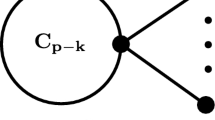
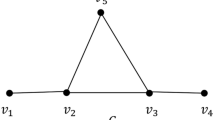
A forest is the clique complex of a strongly chordal graph and a quasi-forest is the clique complex of a chordal graph. Kruskal-Katona type theorems for forests, quasi-forests, pure forests and pure quasi-forests will be presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. Bruns and J. Herzog: Cohen-Macaulay rings, Revised Edition, Cambridge University Press, 1996.

  2. A. Björner: The unimodality conjecture for convex polytopes, Bull. Amer. Math. Soc. 4 (1981), 187–188.

    Article  MATH  MathSciNet  Google Scholar 

  3. R. Charney and M. Davis: The Euler characteristic of a nonpositively curved, piecewise Euclidean manifold; Pacific J. Math. 171 (1995), 117–137.

    MATH  MathSciNet  Google Scholar 

  4. J. Eckhoff: Über kombinatorisch-geometrische Eigenschaften von Komplexen und Familien konvexer Mengen, J. Reine Angew. Math. 313 (1980), 171–188.

    MATH  MathSciNet  Google Scholar 

  5. S. Faridi: Cohen-Macaulay properties of square-free monomial ideals, J. Combin. Theory, Ser. A 109 (2005), 299–329.

    Article  MATH  MathSciNet  Google Scholar 

  6. D. Ferrarello and R. Fröberg: The Hilbert series of the clique complex, Graphs Combin. 21 (2005), 401–405.

    Article  MATH  MathSciNet  Google Scholar 

  7. A. Frohmader: Face vectors of flag complexes, arXiv:math/0605673, preprint.

  8. S. R. Gal: Real root conjecture fails for five-and higher-dimensional spheres, Discrete Comput. Geom. 34 (2005), 269–284.

    Article  MATH  MathSciNet  Google Scholar 

  9. J. Herzog, T. Hibi and X. Zheng: Dirac’s theorem on chordal graphs and Alexander duality, European J. Combin. 25 (2004), 949–960.

    Article  MATH  MathSciNet  Google Scholar 

  10. T. Hibi: What can be said about pure O-sequences?, J. Combin. Theory, Ser. A 50 (1989), 319–322.

    Article  MATH  MathSciNet  Google Scholar 

  11. T. Hibi: Algebraic Combinatorics on Convex Polytopes, Carslaw Publications, Glebe, N.S.W., Australia, 1992.

    MATH  Google Scholar 

  12. G. Kalai: Characterization of f-vectors of families of convex sets in ℝd, Part I: Necessity of Eckhoff’s conditions; Israel J. Math. 48 (1984), 175–195.

    Article  MATH  MathSciNet  Google Scholar 

  13. G. Kalai: Characterization of f-vectors of families of convex sets in ℝd, Part II: Sufficiency of Eckhoff’s conditions; J. Combin. Theory, Ser. A 41 (1986), 167–188.

    Article  MATH  MathSciNet  Google Scholar 

  14. T. A. McKee and F. R. McMorris: Topics in Intersection Graph Theory, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1999.

    MATH  Google Scholar 

  15. P. Renteln: The Hilbert series of the face ring of a flag complex, Graphs Combin. 18 (2002), 605–619.

    Article  MATH  MathSciNet  Google Scholar 

  16. R. Stanley: Combinatorics and Commutative Algebra, Second Edition, Birkhäuser, 1995.

  17. X. Zheng: Resolutions of Facet Ideals, Comm. Algebra 32 (2004), 2301–2324.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Fachbereich Mathematik und Informatik, Universität Duisburg-Essen, Campus Essen, Essen, 45117, Germany

    Jürgen Herzog & Xinxian Zheng

  2. Department of Pure and Applied Mathematics Graduate School of Information Science and Technology, Osaka University, Toyonaka, Osaka, 560-0043, Japan

    Satoshi Murai & Takayuki Hibi

  3. Institute of Mathematics, Vien Toan Hoc 18 Hoang Quoc Viet, Hanoi, 10307, Vietnam

    Ngô Viêt Trung

Authors
  1. Jürgen Herzog
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Satoshi Murai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xinxian Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Takayuki Hibi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ngô Viêt Trung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jürgen Herzog.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Herzog, J., Murai, S., Zheng, X. et al. Kruskal-Katona type theorems for clique complexes arising from chordal and strongly chordal graphs. Combinatorica 28, 315–323 (2008). https://doi.org/10.1007/s00493-008-2319-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00493-008-2319-8

Mathematics Subject Classification (2000)

Search

Navigation