Abstract
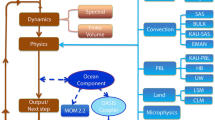
A new version of the general circulation model CNRM-CM has been developed jointly by CNRM-GAME (Centre National de Recherches Météorologiques—Groupe d’études de l’Atmosphère Météorologique) and Cerfacs (Centre Européen de Recherche et de Formation Avancée) in order to contribute to phase 5 of the Coupled Model Intercomparison Project (CMIP5). The purpose of the study is to describe its main features and to provide a preliminary assessment of its mean climatology. CNRM-CM5.1 includes the atmospheric model ARPEGE-Climat (v5.2), the ocean model NEMO (v3.2), the land surface scheme ISBA and the sea ice model GELATO (v5) coupled through the OASIS (v3) system. The main improvements since CMIP3 are the following. Horizontal resolution has been increased both in the atmosphere (from 2.8° to 1.4°) and in the ocean (from 2° to 1°). The dynamical core of the atmospheric component has been revised. A new radiation scheme has been introduced and the treatments of tropospheric and stratospheric aerosols have been improved. Particular care has been devoted to ensure mass/water conservation in the atmospheric component. The land surface scheme ISBA has been externalised from the atmospheric model through the SURFEX platform and includes new developments such as a parameterization of sub-grid hydrology, a new freezing scheme and a new bulk parameterisation for ocean surface fluxes. The ocean model is based on the state-of-the-art version of NEMO, which has greatly progressed since the OPA8.0 version used in the CMIP3 version of CNRM-CM. Finally, the coupling between the different components through OASIS has also received a particular attention to avoid energy loss and spurious drifts. These developments generally lead to a more realistic representation of the mean recent climate and to a reduction of drifts in a preindustrial integration. The large-scale dynamics is generally improved both in the atmosphere and in the ocean, and the bias in mean surface temperature is clearly reduced. However, some flaws remain such as significant precipitation and radiative biases in many regions, or a pronounced drift in three dimensional salinity.
Similar content being viewed by others
1 Introduction
Coupled Atmosphere–Ocean General Circulation Models (AOGCMs) are useful tools to improve our understanding of the climate system (mechanisms, spatio-temporal variability, levels of predictability etc.) and to make future climate projections. Their realism has been regularly improved over the last decades but they still suffer from large biases responsible for part of projections uncertainties of the twentyfirst century climate (IPCC report 2007). The so-called Coupled Model Intercomparison Project (CMIP) provides a standard experiment protocol and an infrastructure that enables a diverse community of scientists to analyse coupled GCMs in a systematic fashion, a process which facilitates model development as well as climate change studies and understanding of past climate fluctuations. Since the 1990s, CNRM-GAME (Centre National de Recherches Météorologiques—Groupe d’études de l’Atmosphère Météorologique) and Cerfacs (Centre Européen de Recherche et de Formation Avancée) have joined their efforts to develop the family of CNRM-CM AOGCMs. ARPEGE-Climat is the atmospheric component (Déqué et al. 1994) of the coupled model, including the ISBA land surface scheme (Noilhan and Planton 1989), while NEMO (Madec 2008) and GELATO (Salas y Mélia 2002) are the oceanic and sea ice components respectively. TRIP (Oki and Sud 1998) is used for river routing and finally the OASIS platform (Valcke 2006) ensures coupling between all the modules.
The previous version of the model, CNRM-CM3, has participated to phase 3 of the CMIP exercise and the corresponding simulations are available on the CMIP3 database. Many studies based on the CMIP3 database have included CNRM-CM3 in their analysis. Following them, it appears that CNRM-CM3 reproduces reasonably well the large-scale circulation (Caballero 2008; Tanaka et al. 2005). For instance, the intensity of the simulated Hadley cell is one of the most realistic of the CMIP3 models. Several studies also stress that CNRM-CM3 is particularly successful in reproducing the Arctic surface climate (Chapman and Walsh 2007; Franco et al. 2011; Liu et al. 2008; Walsh et al. 2008) and the Arctic sea ice cover (Arzel et al. 2006). The Asian monsoon is also reasonably reproduced in CNRM-CM3 (Li et al. 2008). On the other hand, the model has a large cold bias in tropical sea surface temperatures (SST). The mean precipitation is shown to be largely overestimated (Waliser et al. 2007) and the model suffers from the double ITCZ syndrome (Bellucci et al. 2010; de Szoeke and Xie 2008; Lin 2007). The southern ocean circulation is shown to be especially weak (Russell et al. 2006), as pictured by the transport through the Drake Passage. On the contrary, the North Atlantic meridional streamfunction is overestimated (de Jong et al. 2009).
In the context of the forthcoming CMIP5 exercise (Taylor et al. 2009), a new version, namely CNRM-CM5.1, has been developed to address the major deficiencies found in CNRM-CM3. In CNRM-CM5.1, all CNRM-CM components, except TRIP, have been updated while the general framework of the model has been revisited, since ISBA formerly included in ARPEGE-Climat, has been externalised through the use of the SURFEX (SURFface EXternalisée) modelling system developed at Météo-France. The coupling between the different components has received a particular attention to avoid energy loss and spurious drifts.
The purpose of this paper is to describe the different components included in CNRM-CM5.1 as well as the coupling strategy (Sect. 2). The model set-up and external forcing are presented in Sect. 3. The performance of the model is then evaluated in terms of mean state (Sect. 4). Section 5 summarizes the main skills and deficiencies of the model and gives the main conclusions and perspectives. This should provide the scientific community with a background picture of the model that is required to interpret results within a multi-model framework as encouraged in CMIP5 in preparation for the 5th IPCC assessment. A comparison with the CNRM-CM3 previous version of the model is provided when applicable to quantify the improvements. Forthcoming papers will address particular aspects of CNRM-CM5.1 into more details such as sea ice modelling (Salas y Mélia and Chevallier 2012), climate sensitivity and feedbacks (Geoffroy et al. 2011), ENSO-monsoon teleconnections (Kamala et al. 2012, this issue), temperature extremes over Europe (Cattiaux et al. 2012, this issue), etc.
2 CNRM-CM5.1: components and coupling method
2.1 Atmospheric model: ARPEGE-Climat v5.2
The global spectral ARPEGE-Climat atmospheric model is derived from the ARPEGE/IFS (Integrated Forecast System) numerical weather prediction model developed jointly by Météo-France and European Center for Medium-range Weather Forecast (ECMWF). This is a spectral model that operates on a T127 triangular truncation within CNRM-CM5.1 (T63 for CNRM-CM3). All the physics and the calculations of the nonlinear terms require spectral transforms onto a reduced Gaussian grid (Hortal and Simmons 1991) equivalent to a spatial resolution of about 1.4° in both longitude and latitude (2.8° for CNRM-CM3). CNRM-CM5.1 is run in a “low-top” configuration with 31 vertical levels, following a progressive hybrid σ-pressure discretization, whereas CNRM-CM3 was run in a 45 levels configuration, better describing the low stratosphere. It has been decided to reduce the number of levels because of constraints on computing resources (a 91-level stratospheric version based on CNRM-CM5.1. with a lower horizontal resolution has also been designed for chemical studies, but is not discussed here). Nine and four layers are above 200 and 100 hPa respectively; the highest level is set at 10 hPa. At low levels, there are 6 layers below 850 hPa except in regions of high orography.
The dynamical core is based on a two time-level semi-Lagrangian numerical integration scheme tagged as cycle 32 of the ARPEGE/IFS system (cycle 18 for CNRM-CM3). A 30 min time-step is used except for the radiative transfer module called every 3 h for full computation. The model includes six prognostic variables: temperature, specific humidity, ozone concentration, logarithm of surface pressure, vorticity and divergence.
In CNRM-CM5.1, a new longwave radiation scheme is used based on the Rapid Radiation Transfer Model (RRTM, Mlawer et al. 1997) included in the IFS ECMWF model. The radiative transfer equation is solved by a two-stream method. The RRTM scheme computes fluxes in the spectral range encompassing the 10–3,000 cm−1 band. The computation is organized in 16 spectral bands and includes line absorption by H2O, CO2, O3, CH4, N2O, CFC-11, CFC-12, and aerosols. The shortwave part of the scheme, originally developed by Fouquart and Bonnel (1980), integrates the fluxes over the whole shortwave spectrum between 0.2 and 4 mm. The scheme includes Rayleigh scattering, absorption by water vapour and ozone, both varying in space and time, and by CO2, N2O, CO, CH4, and O2, which are treated as uniformly mixed gases. The parameterization has been upgraded by increasing its spectral resolution from 4 to 6 bands, leading to three bands in the UV–visible spectral range (185–250, 250–440 and 440–690 nm) and three bands for the near infrared (690–1,190, 1,190–2,380 and 2,380–4,000 nm). Five tropospheric aerosol types are used: sulphate, organic, black carbon, sea salt and sand dust. Volcanic aerosols can also be specified as a stratospheric aerosol type. As the heating rate associated with historical eruptions was largely overestimated in the former version of the model (SPARC CCMVal 2010), the optical properties of stratospheric aerosols associated to volcanoes eruptions have been revised (in particular their diffusion has been increased). A simple parameterization of the indirect forcing of sulphate aerosols has been introduced following Quaas and Boucher (2005), representing that at constant cloud liquid water content, increasing aerosol concentration leads to a larger concentration of cloud droplets of small radius and increases cloud reflectivity. The ozone-mixing ratio is a prognostic variable with photochemical production and loss rates computed by a 2-D zonal chemistry model (MOBIDIC, Cariolle and Teyssèdre 2007).
The deep convection scheme has been described by Bougeault (1985) and has not changed since CNRM-CM3. Deep convection occurs under two conditions, namely convergence of humidity at low layers and unstable vertical temperature profile. The convection adjusts the unstable profile to a cloudy profile, which is assumed to be moist adiabatic. The scheme uses the mass-flux concept where the vertical ascent in the cloud is compensated by a large-scale subsidence. A Kuo-type closure is assumed where the available moisture is either precipitated or recycled into the environment by the detrainment term.
Stratiform cloud fraction, stratiform liquid water content and coefficients of turbulent vertical mixing as well as Brunt-Väisälä frequency are computed from Ricard and Royer (1993). Sub-grid condensation parameterisation is described in Bougeault (1981, 1982), based on Deardoff (1977) and Mellor (1977). In CNRM-CM5.1, ARPEGE-Climat does not have a prognostic equation for condensate that all precipitates. For the turbulence part, the problem of closure is solved by the sub-grid scheme of order 2 described in Mellor and Yamada (1974, 1982), Yamada and Mellor (1975) and Galperin et al. (1988), in which the effects of liquid water and the water vapour are taken into account. For the mixing length formulation within the boundary layer, the cubic profile used in CNRM-CM3 is replaced by a quadratic profile adapted from Lenderink and Holtslag (2004). The sub-grid condensation scheme accounts for sub-grid condensation in the case of non-precipitating clouds; it leads to account for the cloud fraction and the liquid water amount generated by small-scale turbulence. Large-scale precipitation is computed from the statistical precipitation scheme described in Smith (1990). The Kessler formulation (1969) is used for the evaporation of precipitation.
As the semi-lagrangian dynamical core is not fully conservative (Lucarini and Ragone 2011 and references herein), a mass conserving procedure is activated every 5 days in CNRM-CM3. This conservation procedure has been extended in CNRM-CM5.1 to the atmospheric water content and is there applied every time step.
To sum up, compared to CNRM-CM3, CNRM-CM5.1 benefits for the atmosphere from an increased horizontal resolution, a new dynamical core, a new radiative scheme, water conservation and an improved treatment for ozone and aerosols.
2.2 Surface components: SURFEX and TRIP
Over the past few years, a special effort has been devoted at CNRM to externalize the surface scheme in all coupled surface-atmosphere meso-scale/forecast/climate systems. The level of externalization goes from physical parameterizations to the setup of specific surface parameters needed by physical schemes and the initialization of all state variables of the different subcomponents. In CNRM-CM5.1, this new interface, named SURFEX, includes three surface schemes that represent the surfaces of natural land, inland water (lakes) and sea/ocean areas.
The natural land surface scheme is based on the “Interaction between Soil Biosphere and Atmosphere” (ISBA) model (Noilhan and Planton 1989; Noilhan and Mahfouf 1996). It uses the so-called force-restore method to calculate the time variation of the surface energy and water budgets via a composite soil-vegetation-snow approach. The snow pack evolution is based on a simple one-layer scheme following Douville et al. (1995). The evolution of the soil water is due to surface infiltration, soil evaporation, plant transpiration and deep drainage. The infiltration rate is computed as the difference between the through-fall rate and the surface runoff. The through-fall rate is the sum of the residual of rainfall that is not intercepted by the canopy that drips from the interception reservoir plus the snowmelt from the snow pack.
While ISBA was used in CNRM-CM3, many improvements in land surface hydrology have been introduced in the latest version used in SURFEX. The main developments between the two versions are described hereafter. A more accurate explicit freeze–thaw scheme (Boone et al. 2000) has been added and the soil hydrology is now represented by three layers as opposed to two in CNRM-CM3. Originally, the surface scheme only considered a rooting layer that included a thin surface layer (1 cm depth). An additional layer to distinguish between the rooting depth and the total soil depth (Boone et al. 1999) has been introduced. Only the two uppermost layers can freeze/thaw according to atmospheric and soil temperature conditions. Soil vertical heterogeneity is taken into account via the use of an exponential profile of the saturated hydraulic conductivity with soil depth (Decharme et al. 2006). A comprehensive parameterization of sub-grid hydrology is also included to account for the spatial heterogeneity of precipitation, topography, soil properties and vegetation within each grid cell (Decharme and Douville 2006, 2007). The snow reservoir evolves according to the balance between the snowfall rate, the direct sublimation and the snowmelt. Because the presence of snow modifies the surface radiative balance by increasing the albedo, the snow albedo is treated in ISBA as a prognostic variable, which decreases exponentially or linearly with time depending if the snow is melting or not (Douville et al. 1995). To avoid unrealistic snow accumulation over ice-sheets in CNRM-CM5.1, snow reservoir excess over ice sheets (compared to the initialized values of 30 m snow depth) is converted into a pseudo-calving flux with a time relaxation of 1 year. This flux could be crudely considered as the amount of water that would ultimately return to the ocean from icebergs discharge (cf. Sect. 2.5).
All surface parameters are specified according to the 1-km resolution ECOCLIMAP database developed at Météo-France (Masson et al. 2003). In this database, the soil textural properties are taken from the Harmonized World Soil Database of the Food and Agricultural Organization at 1 km resolution (FAO 2009); vegetation parameters are defined using two vegetation datasets: the Corine Land Cover Archive over Europe and the University of Maryland (Hansen et al. 2000) elsewhere at respectively 250 m and 1-km resolution. Albedo, vegetation roughness length, vegetation fraction and leaf area index are prescribed by decades given a fixed annual cycle. Additionally, fixed values are used for rooting depth, stomatal resistance and emissivity. In the default version, land use changes are not taken into account.
Turbulent surface fluxes over inland water bodies (lakes) are simply parameterized by using the Charnock’s approach to compute the roughness length. The exchanges coefficients at the air–water interface are computed from both the neutral transfer coefficients at 10 m and the Louis (1979)’s functions that depend on the stability of the atmosphere evaluated from the Richardson number. As the lake parameterisation was not validated enough in SURFEX when CNRM-CM5.1 has been designed, the lake water surface temperature is daily updated by extrapolation of the nearest ocean grid point value. To avoid using this crude method on a large number of small lakes, only big lakes have been kept (when the water fraction exceed 50% of the grid area), the others being replaced by natural vegetation.
Conversely, over ocean, calculations are based on the Exchange Coefficients from Unified Multi-campaigns Estimates (ECUME, Belamari 2005) scheme. ECUME includes an estimation of neutral transfer coefficients at 10 m calibrated from five flux measurement campaigns included in the ALBATROS database (Weill et al. 2003). A more detailed description of each campaign can be found in Belamari (2005). The inland water or sea/ocean albedo is computed according to the latitude and the solar angle of each grid-cell. Oceanic grid points are treated as sea ice when ice fraction is greater than 0.5 and the sea ice albedo is directly given by GELATO sea ice model. Over sea ice, fluxes calculations are based on Louis (1979) formulation.
In SURFEX, the exchanges between the surface and the atmosphere are realized through a standardized interface (Polcher et al. (1998); Best et al. (2004)) that proposes a generalized implicit coupling. Note that ARPEGE and SURFEX share the same time-step (30 min). As inputs, each surface grid box gets 8 fields : the lower atmospheric level temperature, specific humidity and horizontal wind components, surface pressure, total precipitation, long-wave, shortwave direct and diffuse radiations. In return, SURFEX computes averaged fluxes for momentum, sensible and latent heat that are sent back to the atmosphere together with the radiative terms (surface temperature, surface direct and diffuse albedo, surface emissivity). SURFEX is run on the same grid as ARPEGE so that no interpolation is needed at the interface between land and atmosphere. The relative areas for the three different surface types (land, inland water, ocean) are set from the global ECOCLIMAP database and are used for weighting in the computation of averaged fluxes.
Finally, the total runoff (surface runoff + deep drainage) simulated by SURFEX feeds the Total Runoff Integrating Pathways (TRIP) river routing model used to convert the latter into river discharge on a daily basis. TRIP thus transfers continental fresh waters towards the ocean and ensures the closure of the global hydrological cycle. TRIP is developed at Tokyo University by Oki and Sud (1998). It is based on a single prognostic equation for water mass within each grid cell of the hydrologic network. In the version used, the stream flow velocity is assumed to be constant and uniform at 0.5 m s−1 over the global river channel network defined at 1° by 1° resolution.
The SURFEX-TRIP system has been extensively validated in off-line mode at the global, continental and basin scales and the reader is invited to refer to Decharme and Douville (2007), Alkama et al. (2010) and Decharme et al. (2010) for more information about the model performance.
2.3 Oceanic model: NEMO v3.2
The ocean component of CNRM-CM5.1 is based on the ocean part of the “Nucleus for European Modelling of the Ocean” (NEMO, version v3.2), a numerical framework developed by several European institutions (CNRS, Mercator-Ocean, UK Met Office and NERC-NOCS). An extensive description of the ocean model can be found in Madec (2008). The global ocean configuration used in CNRM-CM5.1 is known as ORCA-1° (Hewitt et al. 2011). Each configuration of the ORCA family (Penduff et al. 2010) has a tripolar, quasi-isotropic grid: a combination of an isotopic Mercator grid south of 20°N, and a non-geographic quasi-isotropic grid north of it, in which the North Pole singularity is replaced by a line between points in Canada and Siberia. In ORCA-1°, a nominal resolution of 1° at the equator is chosen to which a latitudinal grid refinement of 1/3° is added in the tropics. In the vertical, 42 levels are used (from 10 m at the surface, to 25 at 100 m, 130 at 600 m, and 300 at 5,000 m) and a partial step formulation (Barnier et al. 2006; Penduff et al. 2007) is applied to the thickness of the bottom layer. At the surface, the model has a linear free surface (Roullet and Madec 2000). Advection of temperature and salinity is done using a total variance dissipation scheme (Lévy et al. 2001; Cravatte et al. 2007), a second-order, two-step monotonic scheme with moderate numerical diffusion. Finally, an energy and enstrophy conserving scheme is used (Arakawa and Lamb 1981; Le Sommer et al. 2009).
The mixed layer dynamics is parameterized using an improved Turbulent Kinetic Energy (TKE) closure scheme (Madec 2008), based on the Blanke and Delecluse (1993) TKE scheme plus parameterizations of double diffusion process (Merryfield et al. 1999), Langmuir cell (Axell 2002), Surface wave breaking (Mellor and Blumberg 2004), and using an energetically consistent time and space discretization (Burchard 2002; Marsaleix et al. 2008). The shortwave radiation from the atmosphere is distributed in the surface layers of the ocean using the simplified red–green–blue chlorophyll-dependent attenuation coefficients of Lengaigne et al. (2007) assuming constant chlorophyll of 0.05 g Chl/L. A parameterization of bottom intensified tidally driven mixing similar to Simmons et al. (2004) is used in combination with a specific tidal mixing parameterization in the Indonesian area (Koch-Larrouy et al. 2007) which has been found to significantly impact the behaviour of coupled GCMs (Koch-Larrouy et al. 2010).
The model uses a 1-h time step. Lateral diffusivity is parameterized by an iso-neutral Laplacian operator with an eddy diffusivity coefficient of 103 m2 s−1 at the Equator decreasing with the reduction of the grid spacing with the latitude (it becomes less than 500 m2 s−1 poleward of 60°N and S). In addition a bolus velocity is applied on temperature and salinity (Gent and McWilliams 1990) with the NEMO default of a spatially and temporally varying coefficient (calculated from the local growth rate of baroclinic instability and, between 20°N and 20°S, forced to decrease to vanish at the Equator). Lateral viscosity is parameterized by a horizontal laplacian operator with free slip boundary condition and a eddy viscosity coefficient of 104 m2 s−1 except in the tropics where it reduces to 103 m2 s−1 (except along western boundaries). At the ocean floor, a non-linear bottom friction is applied with coefficient of 10−3 and a background bottom kinetic energy of 2.5 10−3 m2 s−2. The model has a Beckmann and Döscher (1997) diffusive bottom boundary layer scheme with a value of 104 m2 s−1. A spatially varying geothermal heat flux is applied though the ocean floor (Emile-Geay and Madec 2009), which global mean value is 86.4 mW m−2.
Compared to this, CNRM-CM3 was based an older ocean model version (OPA8.0, Madec et al. 1998), an ocean configuration at lower resolution, and different ocean physics. The mesh was not part of the ORCA family but the one presented in Madec and Imbard (1996). It has only one North Pole moved over Siberia, a nominal resolution of 2° at the equator and a latitudinal grid refinement of 1/2° in the tropics. The model had only 31 vertical levels on a z-grid, but with a resolution in the upper 100 meters similar to ORCA-1°. The major differences in terms of ocean physics and numerics are as follows. The time-step was longer (1 h 36 min); no-slip lateral boundary condition was used. It did not use the partial step formulation; and a rigid-lid boundary condition was applied at the sea surface instead of a free surface. Advection of temperature and salinity was done using a second order centered scheme and a simpler enstrophy conserving scheme was used on vorticity term of the momentum equation. The original Blanke and Delecluse (1993) TKE scheme was used as well as their choice for a two band shortwave radiation penetration in the ocean. It did not include any tidal mixing parameterization and, at the sea floor, there were neither bottom friction, nor diffusive boundary layer, nor geothermal heating. The viscosity and diffusivity were larger (ahm0 = 4.104 m2 s−1, aht0 = 2.103 m2 s−1). More details about the ocean model used in CNRM-CM3 can be found in Guémas and Salas-Mélia (2008).
It is worth mentioning here that the Caspian Sea, a closed sea absent from CNRM-CM3 but present in CM5.1, is constrained to keep its mean sea level to zero. Excess or deficit in fresh water over the sea is redistributed uniformly over the open ocean on a daily basis.
2.4 Sea ice model: GELATO v5
The GELATO5 sea ice model is directly embedded in the ocean component of CNRM-CM5.1 and uses the same grid. Sea ice dynamics is computed from the Elastic-Viscous-Plastic scheme proposed in Hunke and Dukowicz (1997). The advection of sea ice is semi-lagrangian, as described by Hunke and Lipscomb (2002). The time-step of dynamics and advection is 6 h. Due to convergence, simulated sea ice is allowed rafting (ice thinner than 0.25 m) or ridging (ice thicker than 0.25 m). These processes are taken into account by a redistribution scheme derived from Thorndike et al. (1975), as described in Salas y Mélia (2002).
GELATO5 includes a sophisticated thermodynamic scheme based on an updated version of GELATO2 formerly included in CNRM-CM3 (Salas y Mélia 2002). In CNRM-CM5.1, four ice thickness categories are considered: 0–0.3, 0.3–0.8, 0.8–3 and over 3 m. Transitions or mergers between these categories may occur either because ice thickness varies thermodynamically or due to sea ice transport. Every slab of ice is divided into 10 vertical layers with enhanced resolution near the top. This higher resolution allows to better capturing rapid surface temperature changes when high frequency variability of the thermal forcing occurs. All ice categories may be covered with one layer of snow, for which snow ageing and snow-ice formation processes are accounted (Salas y Mélia 2002). The thermodynamic scheme uses a time-step of 1 day.
The main developments between GELATO2 and GELATO5 are described hereafter, without giving details about numerical implementation, for the sake of clarity. Following Ono (1967), sea ice specific heat is now a function of ice temperature and salinity. Sea ice massic enthalpy is defined as the amount of energy needed to raise sea ice to melting point, to melt it completely and to raise the meltwater temperature to 0°C, this total quantity multiplied by −1. In GELATO5, massic enthalpy replaces ice temperature as a state variable, except for the iterative solving of the vertical heat diffusion equation in the ice-snow slab.
The specific heat of snow (equal to the specific heat of pure ice), snow conductivity, and ice density are assumed to be constants. Snow density increases as a function of time, and is updated in case new snowfalls occur (Salas y Mélia 2002). The heat conduction coefficient of sea ice is a function of ice temperature and salinity profile as given in Pringle et al. (2007). The salinity profile is computed from the bulk salinity of sea ice by assuming standard salinity profiles for multi-year or young sea ice.
The atmospheric non-solar heat flux at the top of the slab is computed by SURFEX and serves as a boundary condition for the vertical heat diffusion scheme. The other boundary condition is achieved by constraining ice temperature at the bottom ice-ocean interface to sea water freezing point. Solving the heat diffusion equation allows to update the vertical enthalpy profile through the temperature profile of ice and snow. Hence it allows determining if the surface is melting or not. This information is necessary to compute the surface albedo.
The albedo of bare, dry ice albedo is a function of thickness (Flato and Brown 1996). However, this albedo is modulated by the age of sea ice: if an ice slab is older than 6 months its albedo is relaxed to the albedo of thick, dry ice α maxi = 0.71. The albedo of melting bare ice is a model parameter, because it implicitly includes the contribution of surface melt ponds, which are not modelled in GELATO5. Observations of surface albedo obtained at the SHEBA Arctic ice station (see e.g. Curry 2001, Fig. 1) suggest that pond-covered sea ice albedo may reach values as low as 0.4 at the peak of the summer. Its average however lies between 0.5 and 0.6 and the fixed value of 0.56 is chosen accordingly in CNRM-CM5.1 based on several sensitivity experiments. The albedo of snow follows Flato and Brown (1996)’s specification and the fraction of slab covered by snow depends linearly on the snow thickness (converted to liquid water equivalent). The surface albedo is eventually weighed by the snow and bare ice fractions.
Averaged 1970–1999 optical thickness of aerosols used for the 20th century CMIP5 simulations derived from a simulation with the LMDZ-INCA chemical climate model for (top left) black carbon, (top right) sulphate, (mid-left) dust, (mid-right) sea salt, (bottom left) particle organic matter and (bottom right) the sum of all contributions
Solving the heat diffusion equation also allows to assess the conductive heat flux at the sea ice—ocean bottom interface, Q b . The ocean-sea ice sensible heat flux Q o is computed following Schmidt et al. (2004). By convention, the heat flux affecting sea ice is counted positive if it warms up or melts ice. If Q b + Q o ≥ 0, melting takes place at the bottom interface of sea ice and the melting rate can be easily computed since sea ice enthalpy is known. Conversely, if Q b + Q o < 0, sea ice grows from the bottom of the slab. Note that the ice growth rate is computed iteratively, since the enthalpy of newly formed sea ice is a function of salt uptake, the latter being itself a function of the ice growth rate (following Cox and Weeks 1988). The scheme converges within less than 10 iterations, yielding the salinity of sea ice that has formed, and its freezing rate. The same scheme is used when sea ice forms from open water: it occurs if the sea surface temperature reaches the freezing point and if the marine surface loses energy. In this case, Q b + Q o is just replaced with the net surface heat flux. Another phenomenon contributing to salt trapping by sea ice is the formation of snow ice due to infiltration of snow by sea water; this process is also modelled in GELATO5. Gravity drainage and flushing of salt are also taken into account in sea ice bulk salinity changes, following Vancoppenolle et al. (2009). Following a similar method, the vertical enthalpy profile is updated and remapped onto the vertical grid.
2.5 Coupling methodology with OASIS3
In CNRM-CM5.1, the atmospheric component model ARPEGE including the surface model SURFEX, the oceanic component model NEMO including the sea ice model GELATO, and the runoff component model TRIP are run as three separate executables (in the UNIX sense). Within one executable, i.e. between ARPEGE and SURFEX or between NEMO to GELATO, the coupling fields are transferred internally by argument passing. Between the three executables, the OASIS3 coupler (Valcke 2006) is used to synchronize, interpolate and exchange the coupling fields. Interpolation is needed to express on the numerical grid of the target component a coupling field provided by the source component on its numerical grid. All interpolations in CNRM-CM5.1 are based on the Spherical Coordinate Remapping and Interpolation Package (SCRIP) library interfaced in OASIS3. For a detailed description of the regridding, the reader is therefore referred to Jones (1999) and to the SCRIP User’s Guide (see Jones 2001).
The coupling period is currently set to 1 day for all coupling fields managed by the OASIS coupler. At the beginning of day n, each component receives its input coupling fields that have been previously computed and sent by the corresponding source component at the end of day n − 1 and interpolated by the OASIS3 coupler. For the particular case of the first day of the run, OASIS3 reads the coupling fields from coupling restart files. It should be noticed here that land and ocean surfaces are not treated homogeneously since the coupling between the atmosphere and the land surface is done at each atmospheric time step (every 30 min) whereas the coupling with the ocean is done on a daily basis.
2.5.1 ARPEGE-NEMO interface
The coupling fields sent by NEMO to ARPEGE are detailed in “Appendix”, paragraph 3. The first 3 fields (fields 3.1–3.3) are interpolated from the ORCA1 grid to the ARPEGE Gaussian reduced grid with a bilinear interpolation. The sea-and-ice-surface-weighted-temperature is used as a uniform boundary condition over each grid cell for the calculation of the total non solar heat flux (field 4.9) in SURFEX. The surface zonal and meridional current fields (fields 3.4 and 3.5) are calculated by NEMO based on its local u and v components provided in the grid local coordinate system; they are interpolated with a bicubic interpolation.
The atmospheric fields sent by ARPEGE to NEMO through the coupler are listed in “Appendix”, paragraph 4. A mask is applied to the atmospheric field to only use values calculated over the ocean fraction of the atmospheric grid. The zonal and meridional wind stress (fields 4.1 and 4.2) are interpolated with a bicubic algorithm to the ORCA1 grid and NEMO uses this information to construct the components of the wind stress in the grid local coordinate system.
All water and heat fluxes, the wind stress module and the 10 meters wind module (i.e. fields 4.3–4.10) are remapped to the ORCA1 grid using a conservative remapping algorithm. In this algorithm, the weight associated with a source cell for the calculation of a target point value is proportional to the target cell area intersected by the source cell in the latitude-longitude space. For ocean grid cells intersecting a mix of land and ocean atmospheric grid cells, land atmospheric cells are considered as masked, and a normalization is applied using the sum of the non-masked source cell intersected areas to normalize each target cell field value. With this option, the flux is not locally conserved, but the flux has a reasonable value on all target cells. Furthermore, the source nearest unmasked neighbour is used for ocean grid target cells that intersect only land (masked) source cells.
Additional global transformations are also performed on the fluxes by OASIS3; these are needed to ensure global conservation because the size of the seas is not exactly the same in ARPEGE and in NEMO. For all water fluxes except sublimation (i.e. fields 4.5–4.7), and for the total solar heat flux (field 4.10) the field is integrated on the non-masked source and target grids and the residual (i.e. the difference target—source) multiplied by the ratio of the non-masked target surface over non-masked source surface, is distributed proportionally to the value of the original field. This global transformation ensures that the amount of water/energy received is equal to the source energy and that the sign of the field is not changed. No additional global transformation is needed for the sublimation (which is in fact included in the evaporation flux) as it is only a diagnostic field used in GELATO.
A global conservation, analogous to the one applied to the water fluxes except that the residual is uniformly distributed on the target grid, is applied to the total non solar heat flux (field 4.10). It is worth mentioning here that in our case NEMO keeps the solar and non solar heat fluxes over the ice unchanged during a coupling time-step. To ensure global conservation of the energy over water and ice with the evolving sea ice fraction, it is the solar and non-solar fluxes over open water which are adjusted in each cell at each GELATO time-step given the new ice fraction calculated by GELATO.
It is important to note here that, thanks to SURFEX, the atmosphere model can consider 3 types of surface per cell (nature, inland water, ocean). The above coupling exchanges between the ocean and the atmosphere (fields 3.1–3.5 and 4.1–4.10) occur only over the ocean and inland water areas of the atmospheric cells. Therefore, we ensured that the area of the cells considered in the integral calculations described above corresponds to the ocean + inland water part of the cells only.
The Antarctic pseudo-calving calculated in SURFEX is distributed over the ocean non-masked grid points south of 60°S. The same type of transformation is applied to the Greenland pseudo-calving field except that the whole ORCA-1° usual non-masked domain is considered as the target domain.
2.5.2 ARPEGE-TRIP and NEMO-TRIP coupling interfaces
ARPEGE sends only its land cell reservoir overflow to TRIP. In order not to smooth the extreme values of this field, a 1-nearest-neighbor interpolation is chosen in OASIS3 to express the field produced by ARPEGE on the TRIP grid. A global conservation into which the raw difference between the integrated fields over the non-masked source and target grids is distributed proportionally to the value of the original field is then applied.
TRIP uses the land cell reservoir overflow provided by SURFEX to calculate the runoff at its discharge coastal points that is sent to NEMO. In order to remap the runoff appropriately, new coupling masks were defined both for the TRIP grid, with only the land discharge coastal point unmasked, and for the NEMO ORCA-1° grid with only the ocean points belonging to a narrow band along the coast left unmasked. The runoff is remapped from the TRIP land coastal band to the ORCA-1° ocean coastal band with a 6 nearest-neighbour distance-Gaussian-weighted interpolation ensuring that the target points closer to the coast receive more runoff. The same type of global conservation than for the ARPEGE-TRIP coupling is then applied. The reader is referred to Maisonnave and Terray (2008) for more details.
3 Model setup
To initialize a control pre-industrial simulation, a 200-year spin-up simulation has been performed starting from Levitus (Locarnini et al. 2006; Antonov et al. 2006) ocean state at rest, and from climatological thickness and extension for sea ice; its initial atmospheric/land-surface state is drawn from a long-term simulation done with a preliminary version of the model which has ensured that the soil water and snow reservoirs have already reached equilibrium before the spin-up simulation. Both simulations were performed using pre-industrial forcings, with greenhouse gases (GHG) concentrations and solar irradiance fixed to their 1850 values. The optical depths of the five types of tropospheric aerosols are taken from an LMDZ-INCA simulation forced with CMIP5 prescribed emissions (Szopa et al. 2012, this issue; Schulz 2007). For the spin-up and the pre-industrial simulations, we use the averaged 1850–1860 concentrations simulated by LMDZ-INCA as a proxy for pre-industrial concentrations. For sea salt aerosols, the optical depths provided by LMDZ-INCA are re-scaled to obtain a global averaged optical depth equal to the value obtained with the Tegen data (Tegen et al. 1997). This scaling is necessary since Tegen data has always been the original data used in ARPEGE-Climat (then tuned according to this data) and the integrated optical depths obtained with LMDZ-INCA are 5 times higher than with Tegen. The sea salt optical thickness used is quite low compared to AEROCOM multi-model estimates. However, this natural forcing is fixed in all simulations, thus it should not have a large impact on the sensitivity of the model at first order. With such a scaling, the geographical distribution of sea salt is governed by LMDZ-INCA but the total optical depth corresponds to Tegen.
This spin-up simulation is not analysed in this document and is only used to generate equilibrium initial conditions for subsequent model integrations. Two types of experiments are then carried out:
-
a so-called pre-industrial control simulation (hereafter PiCTL) integrated over 800 years. In this simulation, all forcings are fixed to their 1850 values as in the spin-up simulation.
-
a 10-member ensemble of simulations over 1850–2009 (hereafter referred to HIST following the CMIP5 nomenclature) differing only by their initial states taken at 50-year intervals from PiCTL. HIST simulations are forced with a time-evolving historic reconstruction of observed GHGs concentrations and solar incident radiation as specified by CMIP5. For sea salt and sand dust, the optical depths are fixed to their pre-industrial values. On the contrary, for sulphate, organic and black carbon aerosols optical depths evolve following the LMDZ-INCA HIST simulation. An 11-year smoothing is applied on raw data to retain the low frequency evolution of the aerosols fluctuations. Higher interannual variability is not related to emissions variability but to the internal variability of the LMDZ-INCA model that one does not seek to reproduce within the HIST framework. Figure 1 shows the mean optical depth over the period 1970–1999 of the tropospheric aerosols types considered in the HIST simulations. A detailed assessment of this LMDZ-INCA simulation is provided in Szopa et al. (2012, this issue). Volcanic eruptions are also taken into account by prescribing the zonal mean optical thicknesses of the related stratospheric aerosols as diagnosed from Amman et al. (2007).
4 Model evaluation
CNRM-CM5.1 has been primarily developed to provide an updated and improved model to participate in the CMIP5 inter-comparison exercise at the core of the forthcoming IPCC 5th assessment report. A particular care has been devoted to ensure conservation in the model so as to obtain a stable integration under fixed preindustrial conditions (Lucarini and Ragone 2011). In the following sections, unless otherwise stated, mean climate is assessed using the first member of the HIST ensemble of simulations. However, as long as mean climate is considered, we have checked that results do not depend on the selected member. The mean climate is generally computed as the 1970–1999 average and results obtained from CNRM-CM5.1 are quasi systematically contrasted to CNRM-CM3.
Models are validated, when applicable, against observations or their estimations from reanalyses, for mean quantities. As stated in the introduction, it is beyond the scope of this paper to evaluate the model performance in terms of variability.
4.1 Model equilibrium and drift
The energy balance is assessed both from PiCTL to characterize the global equilibria of the model under stable conditions and from HIST since observations are representative of the end of the twentieth century. In Table 1, the surface energy budget quantities are compared to the estimations of Trenberth et al. (2009)—hereafter TR09—based on the CERES dataset (Wielicki et al. 2006) that is representative of the 2000–2004 period. This study has been taken as reference since it is one the latest estimate of the Earth global energy budget but the uncertainties remain large. This comparison shows that CNRM-CM5.1 simulates quite a realistic energy budget with some significant improvements compared to CNRM-CM3. The better simulated upward long-wave flux is related to a change in mean temperature as shown in the following section. It is interesting to note that both CNRM-CM5.1 and CNRM-CM3 have a closed budget at the surface in PiCTL but the balance between net solar and thermal radiations is completely different, whereas turbulent heat fluxes are comparable. On the contrary, the top of the atmosphere energy budget is unbalanced by 3 W m−2. In forced mode, the atmospheric model still has an unbalance of 2 W m−2. As already noticed in Lucarini and Ragone (2011), the semi-lagrangian scheme is not conservative and explains a large fraction of this imbalance. To avoid such a flaw, it would have been necessary to implement an ad-hoc energy conservation procedure as is done for water and mass.
Table 2 shows the net heat flux at the ocean surface (including under sea ice) for PiCTL. In both model versions, the imbalance is very weak and below the traditional level of acceptance fixed to ∓1 W m−2, and in the lower range of CMIP3 models (Lucarini and Ragone 2011). The resulting oceanic drifts are indicated in Table 3. Thanks to the work done to improve the energy conservation in CNRM-CM5.1 and consistently with the weak positive net heat flux, the volumetric temperature has a weak positive trend of 0.04°C per century. This tendency is very small (4 times smaller than in CNRM-CM3) and allows for long integrations without altering the ocean climate significantly. In CNRM-CM3, the ocean heat content has a tendency to decrease whereas the net heat flux is positive providing evidence that there was a problem of energy loss somewhere in the coupling and/or in the model components. Accordingly, the sea surface temperature (SST) drift has been largely reduced in CNRM-CM5.1 and is rather weak (0.01°C per century). On the contrary, the drift in salinity has dramatically increased in CNRM-CM5.1. The cause of this drift is under investigation. A preliminary analysis reveals that a possible reason of this drift could be a wrong formulation of the concentration/dilution flux between sea-ice and ocean. The impact of this error still needs to be quantified. In CNRM-CM5.1, NEMO is run in free surface configuration and sea level is now a prognostic variable in the model. The estimation of future sea level rise within climate change frameworks is a challenging task and the conservation of water has been particularly checked when developing the model. In PiCTL, the drift is equal to 21 cm per century and is still therefore far from being negligible compared to the sea level rise estimate of 17 cm over the 20th century from Church and White (2006). The reasons for such a drift are still under investigation. Preliminary results show that the accumulation of snow over glaciers (except over Greenland and Antarctica) is responsible for 40% of this drift. In the next version of the model, the parameterisation already active over Antarctica and Greenland, which avoids such an accumulation, will be activated over all glaciers. Another part of this drift may be related to the erroneous coupling between sea-ice and ocean but, as for salt, it has not been quantified yet.
4.2 Surface climate
Figure 2 shows the mean surface temperature biases of the model for both boreal winter (DJFM) and summer seasons (JJAS) over the period 1970–1999 for the HIST simulation. Over the continent (ocean), the bias is calculated as the difference between the model and the CRU2 (HadISST) near surface temperature (sea surface temperature) dataset. For both seasons, it is clear that the mean bias and the root mean square error are considerably reduced in CNRM-CM5.1 compared to CNRM-CM3. The new ECUME bulk formulation for surface exchanges at the air-sea interface is mostly responsible for this improvement. Over the ocean, the overwhelming SST cold bias is reduced by half particularly in the tropics and more strongly in summertime. However, warm biases in tropical eastern oceans are still present and somewhat reinforced in CNRM-CM5.1. This warm bias has been already noted in the NEMO oceanic model run in a configuration forced by observational estimates as reported in Griffies et al. (2009) where it is attributed to poorly resolved coastal upwellings and underestimated associated westward mass transport due to the coarse model grid resolution. This oceanic intrinsic deficiency is coupled to the intrinsic misrepresentation of strato-cumulus clouds in ARPEGE as found in so-called AMIP-type forced mode (not shown). This model weakness is shared by most of the state-of-the-art GCMs. As the cloud and convection schemes have not been updated in CNRM-CM5.1, there is no reason to obtain any improvement here when contrasting to CNRM-CM3.
Near surface temperature over continents and sea surface temperature over oceans (K) averaged over 1970–1999. (Left) CNRM-CM3 simulation minus 1970–1999 CRU2.1 (Mitchell and Jones 2005) over continents and CNRM-CM3 simulation minus 1970–1999 HadiSST (Rayner et al. 2003) over ocean, (top) DJFM (bottom) JJAS. (right) same for the CNRM-CM5.1 simulation
At mid-latitudes, austral oceans are dominated by a moderate warm bias that has been greatly reduced in CNRM-CM5.1 especially in austral summer. Biases dropped from 6 to 7 degrees averaged over a latitudinal band to 3–4 degrees at most. Over that region, improvements are attributed on one hand to the increased resolution of the atmospheric component ensuring a better representation of the extra-tropical synoptic storms (see subsequent Sect. 4.3), and on the other hand on the improved vertical mixing in the ocean. Sensitivity experiments have been performed to calibrate the vertical mixing parameters. Tests have shown that the vertical mixing is especially efficient in summertime leading to a reduction of the seasonal over-stratification produced by the ocean model in coupled mode. A new calibration of snow reservoir and albedo within SURFEX over ice sheets also contributes significantly to the warm bias reduction in the Austral region. Snow reservoirs have been increased over Antarctica as well as the albedo minimum value to better represent the ice-sheets surface-atmosphere fluxes. This calibration has resulted in a reduction of the ice-sheet near surface temperature.
In CNRM-CM5.1, a very strong cold bias appears in the Northern Atlantic off Newfoundland. This “blue spot” is a known problem that is amplified in the new NEMO configuration. In Griffies et al. (2009), the intercomparison between seven ocean-ice models forced by observational estimates at the surface clearly reveals this deficiency. All state-of-the-art models at such a resolution have quite large SSTs biases over the North Atlantic that are related to difficulties in correctly positioning frontal zones and simulating complex currents systems and water masses formation.
Over the continents, the overall pattern of errors has not greatly evolved between the two model versions, even if biases have been weakly reduced in the global average. This is particularly striking in DJFM over northern Siberia where the strong cold bias is partially reduced, as well as the intense DJFM warm bias over central Eurasia and western Canada. These improvements may be attributed to the more accurate soil freezing parameterisation implemented in ISBA (Boone et al. 2000). Conversely in boreal summer, a significant warm bias appears in CNRM-CM5.1 over Eastern Europe and most of northern America. This warm bias seems related to a deficit in total cloud cover (not shown) and associated excess of incoming solar radiation at the surface. A positive feedback involving the land surface further enhances this radiatively driven temperature bias: excess of radiation favours spring and early summer soil evaporation leading to soil drying and a subsequent deficit in evapotranspiration as summer goes on. Simulations done with SURFEX in off-line mode support this hypothesis. These two processes lead to a progressive decrease in rainfall rate that ultimately favours the persistence of this warm bias. In addition to atmospheric processes, ISBA is known to slightly overestimate the evapotranspiration over mid-latitudes low vegetation areas (Calvet et al. 1999; Boone et al. 1999; Habets et al. 1999; Decharme et al. 2011a). This fact can be related to uncertainties in LAI measurements and in other vegetation parameters, as well as in the simple Jarvis stomatal resistance approach. The evaporation deficit in late summer may also be due to the lack of seasonal floodplains and aquifers in the current version of the ISBA-TRIP hydrology. Decharme et al. (2011b) have shown that by introducing seasonal floodplains in the model, runoff is reduced and evaporation is enhanced in late summer.
Mean sea level pressure (MSLP) errors have been greatly reduced almost everywhere in CNRM-CM5.1 (Fig. 3). In the tropics and at mid latitudes, the improvement is mainly attributed to changes in the dynamical core of the atmospheric model (inherited from ECMWF developments). Over austral oceans the use of ECUME sea-surface flux formulation in CNRM-CM5.1 instead of Louis (1979) in CNRM-CM3 clearly contributes to the enhanced skill of the new version. In case of strong surface wind, ECUME wind stress is much smaller than Louis’ one leading to weaker momentum energy passed from the atmosphere to the ocean. The more energetic low-level atmosphere tends in turn to deepen low pressure synoptic systems leading to a clear reduction of the positive MSLP bias in CNRM-CM5.1. In the Northern Hemisphere, the amplitude of the stationary wave is weaker in the North Atlantic compared to ERA40 (Uppala et al. 2006) leading in both seasons to slackened Icelandic Low and Azores High to a lower extent. The underestimated meridional pressure gradient over Europe favours zonal circulation especially in winter. Note though that such a bias has been considerably reduced in the new version of the model in association with the new dynamical core as well as a fine tuning in coupled mode of the gravity wave drag parameter. In the North Pacific, the wintertime stationary wave is slightly too strong in CNRM-CM5.1 by contrast to CNRM-CM3 but errors are quite weak and less than 1 hPa in boreal summer.
As to precipitation (Fig. 4), regional biases have not been significantly reduced since CMIP3 despite a slight improvement of both mean biases and root mean square errors. The primary model deficiency lies in the simulation of the so-called double ITCZ (Lin 2007) referring to the simulation of excess precipitation in the tropical Southern Hemisphere associated with its overestimated seasonal latitudinal migration. Such a model deficiency is clearly worsened in coupled mode in response to warm SST biases in the eastern side of the tropical basins. The weak model improvement between CNRM-CM5.1 and CNRM-CM3 (reduction of the amplitude and zonal extension of the double ITCZ) is mainly attributable to the increased horizontal resolution, which also leads to a reduction of orographic precipitation biases (Himalaya, Andes, Eastern Africa…). However, due to the above-described warm atmosphere/land surface feedback, underestimation in JJAS precipitation appears over Eastern Europe and central North America in CNRM-CM5.1. Note also a clear monsoon rainfall deficit for the Indian peninsula in the new version whose origin is still under investigation.
Precipitation differences (mm day−1) for (left) averaged 1970–1999 CNRM-CM3 minus 1979–1999 averaged GPCP data (Adler et al. 2003) and (right) CNRM-CM5.1 minus GPCP. (top) DJFM (bottom) JJAS
4.3 Atmospheric climate
As stated in Sect. 2, the use of the RRTM radiative scheme for long-wave radiation combined with significant improvements for solar radiation is one of the major changes introduced in CNRM-CM5.1. Impacts are striking on the atmospheric temperature biases (Fig. 5, top) that are reduced by a factor of 2 when integrated vertically. The maximum error in CNRM-CM3 was −13 K in the lower stratosphere whereas the maximum error in CNRM-CM5.1 is only −5 K at the tropopause. We verify that the improvement of the low stratosphere temperature is not due to changes in the model top layer between the two versions: comparable biases are indeed obtained when running CNRM-CM5.1 in stratospheric mode similarly to CNRM-CM3 (60 vertical layers instead of the actual 31 ones).
In line with the thermal wind relationship, zonal wind biases are also clearly reduced in CNRM-CM5.1 especially in the Southern Hemisphere where the jet was too narrow in latitudinal extent and too strong in amplitude (Fig. 5, bottom). In CNRM-CM5.1, its strength is now correct and its northward extension is better captured, still slightly underestimated though compared to ERA40.
Changes in mean atmospheric climate are summarized on Taylor diagrams (Taylor 2001). Figure 6 (top row) shows the scores for the prognostic variables of the model at three atmospheric pressure levels (850, 500 and 200 hPa). The left column shows the change in AMIP type runs (atmospheric model used with forced SSTs), whereas the right column shows the change in the coupled model (from CNRM-CM3 to CNRM-CM5.1). Figure 6 highlights that the score improvement (or worsening) obtained in AMIP mode are qualitatively preserved in coupled mode. This confirms that the improved behaviour of CNRM-CM5.1 is not fortuitous as it could be when coupling model components; it also validates the working strategy of improving the model components separately in a “forced” mode as an efficient way to improve the realism of the coupled model.
Taylor diagrams summarizing the comparison of the CNRM-CM3 and CNRM-CM5.1 models over the period 1970–1999, the arrows indicate the evolution of the fields shown from CNRM-CM3 to CNRM-CM5.1. The correlation is the spatial correlation between annual mean fields and the variance is calculated as the spatial variance of the annual mean field. (Left) for the respective atmospheric models run in AMIP mode (SST forced), (right) for the coupled models. On the top, prognostic variables are shown compared globally to the ERA40 reanalysis over the period 1970–1999 for three levels 850, 500 and 200 hPa (psl = sea level pressure, ta = atmospheric temperature, ua = zonal wind, va = meridional wind, hus = specific humidity, zq = geopotential). At the bottom, the surface net long-wave (rls) and shortwave (rss) fluxes are compared to the ISCCP-d2 dataset (Rossow et al. 1996) over the latitudes 60S–60 N, the outgoing long-wave (rlut) and shortwave (rsut) radiation at the top of the atmosphere as well as the long-wave cloud radiative forcing (lwcrf) and the short-wave radiative forcing (swcrf) are compared the the CERES data (Wielicki et al. 2006) over the latitudes 60S–60 N, the precipitation is compared to the GPCP data (Adler et al. 2003) globally
Whatever the altitude, scores are considerably improved for the winds (ua, va) and geopotential (zg) in CNRM-CM5.1, and the improvement is even larger for mean sea level pressure (psl) as already shown in Fig. 3. For temperature (ta), those are only weakly improved, except at 200 hPa, consistently with the zonal mean biases reduction shown in Fig. 5. The sole variable that is degraded is specific humidity (hus) at all levels. The drop in RMS is due to a strong under-estimation of the standard deviation associated with a mean specific humidity much lower in CNRM-CM5.1 than in ERA40.
Concerning the atmospheric radiative budget (Fig. 6, lower panel), skills that were already good in CNRM-CM3 for upward solar (rsut) and outgoing long-wave fluxes (rlut) on top of the atmosphere are slightly improved as well as for the surface net solar flux (rss). Conversely, scores for long-wave surface fluxes (rls) are clearly better although the correlation with the ISCCP-d2 data (Rossow et al. 1996) is still quite poor. Similar results in AMIP and coupled mode suggest that the use of the new RRTM long-wave scheme is partly responsible for the improvements. In coupled mode, the latter are even larger probably due to reduction in surface temperature biases in that case.
As to cloud radiative forcings (CRF), the correlation with the CERES data is not better in CNRM-CM5.1 whereas the standard deviation is now under-estimated while it was over-estimated in CNRM-CM3. Spatially compared to the CERES estimations (Fig. 7), the solar CRF (swcrf) is somewhat improved in CNRM-CM5.1 (RMS error and mean bias are reduced) but the regional biases are still quite important. Note that the clear sky diagnostics were only stored every 3 h (radiative scheme time-step) in CNRM-CM3 thus explaining the stripes observed in the figures for this version of the model. Interestingly, the model goes from overall SW-CRF negative biases in CNRM-CM3 to positive errors except along the convective region. Unyielding patches of positive SW-CRF are found in the eastern margins of the tropical oceans. As suggested by Taylor diagrams (Fig. 6), the model performs similarly in forced and coupled modes. The positive SW-CRF found in the eastern margins of the tropical oceans may thus be mainly associated with the misrepresentation of the strato-cumulus clouds (Lauer et al. 2010). This bias is found in most of state-of-the-art models at such a horizontal and vertical resolution. Note that in CNRM-CM5.1, there are positive SW-CRF errors over land in northern mid-latitudes. The raw SW-CRF field is negative everywhere so this equates to a reduction in the magnitude of the shortwave cloud forcing consistent with a decrease in cloud cover (not shown) and precipitation (Fig. 4) over these regions. These biases are the largest in boreal summer (not shown). As already explained in the previous section, such seasonal biases are intensified through soil moisture positive feedbacks. SW-CRF biases over northern mid-latitude are partly compensated by underestimated LW-CRF (which are positive). By symmetry, the model goes from positively biased LW-CRF in CNRM-CM3 to negatively biased in CNRM-CM5.1 leading in fine to a less biased global CRF in the new model.
(Top) annual mean solar cloud radiative forcing differences (W m−2) for (left) CNRM-CM3 simulation averaged over 1970–1999 minus CERES data, (right) CNRM-CM5.1 simulation minus CERES data. (mid) as on top for annual mean long wave cloud radiative forcing. (bottom) as on top for annual mean total radiative forcing
Overall, the primary change in CRF is explained by a mean change due to the modification of the partitioning between long-wave and short-wave radiation. Beyond CNRM-CM5.1, there is a clear need to adjust the cloud scheme and probably the convection scheme according to these changes. CRF biases should be kept in mind when analysing the model sensitivity to increased GHG concentrations and the differences between CNRM-CM3 and CNRM-CM5.1 in this respect.
4.4 Ocean climate
4.4.1 Ocean surface
SST mean biases have already been discussed in Sect. 4.2; Fig. 8 shows the interannual SST standard deviation (STD) for both model versions and its estimation from the HadSST1 dataset. Averaged globally, SST STD is largely over-estimated in CNRM-CM3. Values in the ENSO band are two times higher than observed. Biases in STD are considerably reduced in CNRM-CM5.1 in the tropical Pacific. The westward extension of the large STD values in the western Pacific has also been diminished. On the contrary the coastal STD extension from Galapagos Archipelago to the South American coast is now clearly underestimated inhibiting T-Mode ENSO variability initiated in the eastern Pacific (Trenberth and Stepaniak 2001). Maximum STD are found along the Kuroshio and Gulf Stream as well as along the sea-ice edges especially in the Greenland Sea. The latter is associated with strong sea-ice variability. The former are too intense and too zonal especially in the Atlantic, where the Gulf Stream flows zonally from the eastern North American coastline to the Western European coastline (along which the North Atlantic Current flows northward to the Nordic Seas).
To validate Sea Surface Salinity (SSS), we use the EN3 dataset (Ingleby and Huddleston 2007) that includes observed subsurface ocean temperature and salinity profiles (with data quality information), interpolated on a regular grid through objective analysis on a monthly basis from 1950 onwards. SSS errors in CNRM-CM5.1 are very different from CNRM-CM3 (Fig. 9). CNRM-CM5.1 is much fresher partly due to a significant drift in the model tri-dimensional salinity due to coupling flaws. Underestimated SSS are found everywhere but in the tropical North Atlantic and off Central America coast as well as in the Arctic basin. CNRM-CM3 is too salty in the North Pacific, especially in the eastern side of the basin due to anomalous atmospheric circulations that yield too strong evaporation. Indian and Atlantic oceans except in the Labrador Sea are too fresh in CNRM-CM3. CNRM-CM5.1 shows positive SSS biases in the Bay of Bengal and in the Arabian Sea associated with a deficit of precipitation/runoff in the monsoon regions. Over the North Atlantic, the main biases are found off Newfoundland with too fresh SSS by more than 4psu. This “blue spot” is common to many models at such an horizontal and vertical ocean component resolution that does not explicitly resolve transports by eddies (Griffies et al. 2009).
Annual Mean Surface salinity differences in psu (left) between the CNRM-CM3 century simulation (1960–1999) and the EN3 data (Ingleby and Huddleston 2007) averaged over the period 1960–1999, (right) same for CNRM-CM5.1
Latent heat fluxes over oceans are still overestimated in CNRM-CM5.1 (Fig. 10). The water cycle in ARPEGE is known to be particularly strong whatever version is considered. This global overestimation may thus be attributed to the atmospheric model. However, at second order, the overestimation found in the sub-tropics is partly due to overestimated trade winds. Additionally, the largest biases found in the eastern tropical basins are associated with an excess of radiation in line with the absence of low clouds and the weak cloud radiative forcing of clouds (Fig. 7) in this region. Reduced latent heat release is found along the Gulf Stream due to very cold SST biases.
Annual mean latent heat flux in W m−2 (contour) of the CNRM-CM3 simulation (1970–1999) and its difference (shading) to the oaflux data (1970–1999) on left (Yu and Weller 2007). Same for CNRM-CM5.1 on right
The simulated mixed layer depth (MLD) is compared to the reconstructed observed climatology of de Boyer Montégut et al. (2004). Note that the model diagnostic computed from turbulent mixing is not exactly equivalent to the one in the observations based on a temperature criterion. Note also that the comparison between the two model versions is not completely fair since diagnostics are not strictly equivalent. In CNRM-CM3.1, the diagnostic is based on monthly mean averaged MLD whereas in CNRM-CM5.1, the diagnostic is the monthly average of daily maximum MLD. With such a difference, MLDs are expected to be shallower for CNRM-CM3 which is opposite to what is observed in the Northern Hemisphere. This allows to conclude that mixed layer were generally too deep in CNRM-CM3, especially in the Northern Atlantic. Additionally, Fig. 11 suggests that MLD are much better represented in CNRM-CM5.1. In particular, the location of maxima is quite realistic both in the southern oceans and in the Northern Atlantic. Similarly the shallow mixed layers in the tropics are also better captured in CNRM-CM5.1, even if persistent biases are still present in the western part of both Pacific and Atlantic oceans.
Composite of mixed layer depth for March in the Northern Hemisphere and September in the Southern Hemisphere. (top) monthly mean mixed layer depth for CNRM-CM3, (middle) monthly averaged daily maximum mixed layer depth for CNRM-CM5.1, both are averaged over the period 1970–1999 of the HIST simulation; (bottom) climatology of de Boyer Montégut et al. (2004) based on the temperature criterion. For both models, the mixed layer depth is defined by the mixing scheme
4.4.2 The Atlantic Meridional Overturning Circulation (AMOC)
Figure 12 shows the mean vertical profile of the Atlantic meridional stream function for CNRM-CM3, CNRM-CM5.1, NEMO-FOR and NEMO-VAR averaged over 1960–2000 together with the mean observational estimate from moored array instruments through the RAPID section at 26.5°N (Cunningham et al. 2007) averaged over 2004–2009. NEMO-FOR and NEMO-VAR stand respectively, for a stand-alone ocean experiment forced by the so-called DFS4 dataset (Brodeau et al. 2009) and for an ocean reanalysis produced by ECMWF within the COMBINE project (Balsameda et al. 2010, http://www.combine-project.eu/Technical-Reports.1668.0.html) using the same version for NEMO as in CNRM-CM5.1. MOC observational estimates from RAPID reach a maximum value of around 19 Sv at 1,000 m depth approximately. CNRM-CM3 (CNRM-CM5.1) simulates a stronger (weaker) MOC at 22 Sv (13–14 Sv) located at deeper (lower) levels (1,600 m, 800 m). It is interesting to highlight here that the MOC absolute value in CNRM-CM5.1 is similar in NEMO-FOR and NEMO-VAR. This suggests that this NEMO configuration (1° resolution, mixing scheme parameters) may set the MOC absolute value at first order; the depth for the maximum may be more dependent on the forcing.
Figure 13 shows that the AMOC in CNRM-CM5.1 is shallower and much weaker than in CNRM-CM3 over the whole Atlantic Ocean. In CNRM-CM3, the cold SST and positive SSS biases at high latitudes in the North Atlantic led to overestimated North Atlantic Deep Water (NADW) formation, consistent with the over-estimated mixed layer depth shown in the former section, which is not the case in CNRM-CM5.1 where the largest SST and SSS biases at the surface are associated with the “blue spot” described above (and located away from the convective regions). At the sub-surface, maximum temperature biases in CNRM-CM5.1 are found at ~600 meter depth from 30°S to 30°N and are associated to positive salinity biases. Those are linked to Antarctic Intermediate water (AAIW) masses whose properties in CNRM-CM5.1 are significantly different from observations in line with the overly warm SST bias in the Austral Ocean where AAIW forms (Fig. 2).
4.4.3 The meridional heat transports
Figure 14 shows the latitudinal total heat transport for the global and Atlantic-only ocean for the two model versions together with NEMO-FOR, NEMO-VAR and an independent estimate from satellite and reanalysis products (Fasullo and Trenberth 2008, hereafter FT08). At global scale, the total northward heat transport is overestimated (underestimated) in CNRM-CM3 (CNRM-CM5.1) in the Northern Hemisphere compared to FT08. When contrasted to NEMO-FOR and NEMO-VAR, both versions simulate a northward heat transport that is slightly weaker than FT08. The southward heat transport in the Southern Hemisphere is underestimated in both models within the tropical band compared to FT08 or NEMO stand-alone products. Between 30°S and 60°S, the southward transport is close to zero or even reversed except in CNRM-CM3 but recall that observation quality is poor in this region. The sign reversal is shared between ocean stand-alone and CNRM-CM5.1 experiments suggesting that the NEMO version (resolution, parameterization etc.) sets this property. In the Atlantic, CNRM-CM5.1 and NEMO-FOR are very close and about 35–40% weaker than in CNRM-CM3; this is consistent with the slackened MOC in the latest version of the model. Values are within the observational envelope given in Trenberth and Caron (2001).
Northward total heat transport (PW, 1PW = 1015 W) for the global ocean (top) and the Atlantic ocean (bottom) for CNRM-CM3 (red dashed line) averaged over 1970–1999 and CNRM-CM5.1 (red solid line), NEMO-FOR (green line) and the NEMO-VAR (blue line). The NCEP-derived estimate by Fasullo and Trenberth (2008) is also indicated for global ocean heat transport (black line)
4.4.4 Mean transports trough critical sections
Table 4 indicates the mass transport trough some critical sections for CNRM-CM5.1, NEMO-FOR and NEMO-VAR together with observational estimates found in literature similarly to Shaffrey et al. (2009). For Bering, Denmark Straits and Iceland-Scotland passage, CNRM-CM5.1 is in very well accordance with observational estimates as well as the NEMO forced products.
The Fram Strait transport is clearly underestimated in CNRM-CM5.1 as well as in NEMO-FOR and NEMO-VAR to a lesser extent though. The transport trough the Florida Strait in CNRM-CM5.1 is also lower than its observational estimate as in NEMO stand-alone experiments. The underestimation of these transports is thus probably a NEMO property due to the poor representation of the ocean dynamics in the western Atlantic basin in such a coarse resolution model.
The Indonesian Through Flow (ITF) is slightly stronger in CNRM-CM5.1 than in the observational estimates but appears to be more realistic than in NEMO-FOR and NEMO-VAR. This overestimation is a common feature of coarse resolution ocean models that cannot take into account the complex topography over the Indonesian archipelago.
Finally, the mass transport trough the Drake Passage gives an indirect evaluation of the Antarctic Circumpolar Current (ACC) strength. CNRM-CM5.1 significantly underestimates this transport by about 40 Sv compared to the observational estimates. On the contrary, it is slightly overestimated in NEMO-FOR and NEMO-VAR but lies within the uncertainty range of observations in this region. Reasons for the underestimation of the Drake Passage transport in CNRM-CM5.1 are multiple and complex. It is linked to slackened surface fluxes. In particular, wind stresses are clearly underestimated all over the austral ocean due to the equatorward latitudinal shift and the slackening of the extratropical storms in the atmosphere (Fig. 3). This inhibits the vertical mixing and favours a warm bias in SSTs leading to a positive coupled feedback (Fig. 2).
Figure 15 shows the mean barotropic stream function (BSF) computed for CNRM-CM5.1. The shape and position of the main currents and gyres are well represented in the model, except for the Gulf Stream and Kuroshio currents that are too zonal, as already mentioned. Mean values of the BSF over the critical regions are in accordance with observational estimates. Subpolar gyre maximum values are around 30 Sv and even stronger over the Labrador Sea (33 Sv). These values are in agreement with estimates given by Clarke (1984) for 34 Sv over the Southern Greenland. The simulated strength of the Florida current is consistent with estimates of about 30 Sv provided by Schott et al. (1988). The Kuroshio BSF values for CNRM-CM5.1 range from 40 to 60 Sv (max 57 Sv). Estimates derived from altimeter products give approximately 42 Sv on average over the south of Japan (Imawaki et al. 2001). The maximum value of the BSF trough the Drake Passage is 92 Sv, confirming the underestimation of the ACC.
4.5 Sea ice
4.5.1 Arctic sea ice
The Northern Hemisphere geographical distribution of sea ice is generally well simulated in CNRM-CM5.1, particularly in winter (Fig. 16). The simulated ice edge is improved in all regions compared to CNRM-CM3, with the exception of the Greenland Sea where the Odden ice tongue feature is still not reproduced due to the relatively low horizontal resolution of the ocean-sea ice model. The simulated lack of sea ice in Davis Strait and Labrador Sea due to the anomalous transport of warm Gulf Stream waters to this region is less pronounced than in CNRM-CM3. In the Barents Sea, the simulated ice edge is now very close to observations. This is due to a more realistic simulation of the northward ocean heat transport north of 60°N into the Nordic Seas in CNRM-CM5.1. The simulated mean seasonal cycle of north hemisphere sea ice extent is compared to observations in Fig. 17. The latter are SSMR data until June 1987, then SSM/I data until 1999 (Fetterer et al. 2002) and are provided by NSIDC (Boulder, Colorado, USA). This comparison suggests that the simulated total north hemisphere sea ice extent (Caspian Sea excluded for a comparison with NSIDC data) is overestimated by 1.7 × 106 km2 in CNRM-CM5.1 during the winter. However, this bias estimation is rather uncertain, due to significant uncertainties in the observations themselves. About half of this bias is due to an overestimation of sea ice concentration in the Sea of Okhotsk and east of the Kuril Islands. The apparent better simulated annual cycle in CNRM-CM3 is due to errors compensation. On the one hand, the total surface of the Arctic Ocean and peripheral seas north of 60°N in CNRM-CM3 (15.12 × 106 km2) is nearly 2 × 106 km2 smaller than the same surface estimated from ETOPO5 (Table 5) because the Baltic Sea was not included in CNRM-CM3 and the Canadian Archipelago was considered as land. Table 5 also shows that all the ocean surfaces are much closer to ETOPO5 in CNRM-CM5.1 than in CNRM-CM3. This smaller than observed ocean grid surface causes an artificial negative bias in the modelled sea ice extent of about 1.5 × 106 km2 during the winter in CNRM-CM3. This negative bias is broadly compensated by a large overestimate of the sea ice extent in the North Pacific. The total Arctic sea ice extent is underestimated from August to November in CNRM-CM5.1 due to a significant underestimation of sea ice off Alaska and over the eastern part of the Siberian basin (Fig. 16). PIOMAS (Pan-Arctic Ice-Ocean Modeling and Assimilation System) provides reliable estimates of Arctic sea ice thickness over 1979–2011, which can be reasonably seen as a proxy for reality (Schweiger et al. 2011). In the Central Arctic, the simulated mean sea ice thickness in CNRM-CM5.1 is 1.8 m and 0.9 m for March and September respectively, over 1979–1998. A comparison of the simulated sea ice thickness field with PIOMAS (Fig. 15) suggests that these values are probably about 1 m too low. Specifically, the thickness of sea ice is underestimated year-round by up to 2 m North of Greenland, and this bias is close to zero near the Siberian coast. However, the dynamics of sea ice is generally well simulated (Salas y Mélia and Chevallier 2012), suggesting that the simulated structure of winds is improved in the Arctic compared to CNRM-CM3. In particular, the transpolar drift and the Beaufort gyre circulation patterns are realistic even if ice velocities are too high north of Alaska, probably due to the underestimated ice thickness in this region acting as a positive feedback. A direct consequence of the thinner sea ice simulated in CNRM-CM5.1 in most of the Arctic is that the annual mean ice flux at Fram Strait, at 1,293 km3 year−1, is 42% too low compared to observational estimated by Kwok et al. (2004) on the 1991–1998 period.
Sea ice thickness averaged over 1979–1998 for CNRM-CM3 (left) and for CNRM-CM5.1 (middle). PIOMAS data are plotted to the right for the Arctic. The first and second rows respectively represent Arctic March and September ice thickness. The third and fourth rows respectively represent Antarctic March and September ice thickness. The mean 1979–1998 ice edge (thick black line) is defined as the 15% sea ice fraction contour computed from the HadISST data (Rayner et al. 2003)
Mean seasonal cycles of Arctic (left) and Antarctic (right) sea ice extents (106 km2) for 1979–1998. Sea ice extent is defined here as the area enclosed in the 15% sea ice concentration contour. Dashed red CNRM-CM3, solid red CNRM-CM5.1, solid black satellite observations provided by NSIDC (Boulder, Colorado, USA)
4.5.2 Antarctic sea ice
The simulated mean annual cycle of Antarctic sea ice is not improved in CNRM-CM5.1 compared to CNRM-CM3 (Fig. 17). Sea ice still nearly disappears during the austral summer favouring an unrealistic warming of the upper ocean layers (Fig. 2) due to the absorption of incoming solar shortwave energy. Acting as a positive feedback at fall, this warm bias of the upper ocean hampers the formation of sea ice. The persistence of warm surface temperatures cannot be invoked to explain austral winter biases. Figure 16 shows that the simulated Antarctic sea ice extent is underestimated by 1.6 × 106 km2 in September and Fig. 16 highlights that the simulated ice edge is too close to the Antarctic continent in most of the Indian Ocean sector due to bias in atmospheric circulation. Note though that the modelled September sea ice is generally thicker in CNRM-CM5.1 than in CNRM-CM3 (0.57 m and 0.37 m respectively), which is more realistic. The maximum sea ice thickness in CNRM-CM5.1 is about 2 m and is located along the eastern coast of the Antarctic Peninsula, in agreement with data compiled by the ASPeCt group (Worby et al. 2008). However, ASPeCt also reports relatively thick ice (2 m) in the eastern Ross Sea, close to the coast, which is not reproduced in CNRM-CM5.1.
5 Conclusions
This paper provides a description of a new global climate model referred to as CNRM-CM5.1 developed jointly by CNRM-GAME and Cerfacs. A basic evaluation based on a long control integration where external forcings are kept constant and on a twentieth century simulation where they evolve following observational estimates is presented. Within the CMIP5 framework, additional historical, scenario and decadal simulations done with this model version will be made available to the scientific community for model intercomparison studies. The present study should be thus considered as a support material to help scientists interpreting their results in CMIP5 multi-model analyses. The main qualities and shortcomings of CNRM-CM5.1 are presented in terms of preindustrial equilibrium and present-day climatology, and results are compared to those of the previous CMIP3 model version referred to as CNRM-CM3.
Equilibria of the model have been considerably improved in order to ensure that the model could be used for millennium time-scale integrations. In terms of global energy, the SST model drift that is equal to +0.01°C per century is very weak. Regionally, ocean water masses still have some significant biases that are due to the model performances but also to intrinsic characteristics of the physics and dynamics imposed by the spatial and vertical resolutions. The main bias is found in global volumetric salinity that drifts linearly by 0.011 psu/century. We assessed though that this drift does not strongly alter ocean dynamics such as the MOC.
As for present-day mean climate, a clear reduction of biases in terms of surface mean temperature, sea level pressure among others is found in CNRM-CM5.1 versus CNRM-CM3. The atmospheric large-scale circulation has been improved in many regions. Major errors in seasonal precipitation and cloud radiative forcings are however still present such as the double-ITCZ, the critical underestimation of low clouds on the eastern side of the tropical ocean basins, or the lack of cloudiness over the Northern Hemisphere continents. Beyond CMIP5, this suggests the need to revise the convective and cloud parameterisations in CNRM-CM. In terms of ocean mean climate, biases are clearly reduced. The large-scale ocean circulation is reasonably simulated. The MOC amplitude is only slightly underestimated compared to observational estimates. The representation of sea ice is also more realistic over the Arctic while over the Antarctic it is still critically underestimated during the austral summer.
Improvements of the mean present-day climate are not a guarantee that climate sensitivity is now better represented in the model. Efforts have been devoted to the latter to better simulate the effect of aerosols: the indirect effect of sulphate aerosols has been included and stratospheric aerosols properties associated to volcanoes eruptions have been revised. As a perspective, Fig. 18 shows the historical evolution of the annual mean of the global combined land and marine surface temperature anomalies compared to HadCRUT3 (Brohan et al. 2006; Rayner et al. 2006). It is found that the sensitivity of CNRM-CM5.1 to the combination of observed natural and anthropogenic forcings over the twentieth century is far more realistic than in CNRM-CM3. Further analyses are necessary to understand the model underestimation of the observed cooling in the early 1900’s and in the 1950–1960’s. More investigations are especially needed to validate the sensitivity to individual forcings. To address this question, the comparison with the other CMIP5 models will be crucial.
(Black) global annual mean combined land and marine surface temperature anomalies from the reference period 1961–1990 given by the HadCRUT3 data (Brohan et al. 2006, Rayner et al. 2006) in K, (dashed red) CMIP3 and (solid red) CMIP5 simulated temperature for the first member of the ensemble of twentieth century simulations. The red shaded area indicates the range of values simulated by the ensemble of 10 CMIP5 simulations done with CNRM-CM5.1. The thin gray line pictures the ensemble mean. Model data are interpolated on the HadCRUT3 grid and only grid points where hadCRUT3 data are available are taken into account to calculate the global means
Finally, note that this paper is not aimed at providing a comprehensive evaluation of CNRM-CM5.1, but just a broad picture of its global performance over recent decades. Forthcoming studies will illustrate more specific aspects of CNRM-CM5.1. Additional information on the model and on the CMIP5 experiments performed with it can be found at http://www.cnrm.meteo.fr/cmip5/. This model version is also intended to be a solid basis for the inclusion of further developments, that will involve the improvement of the existing components (atmospheric physics, surface cold processes, surface and sub-surface hydrology) as well as the inclusion of new components that are being developed such as land and ocean biochemistry, atmospheric chemistry and interactive aerosols and ice-sheets.
References
Adler RF, Huffman GF, Chang A, Ferraro R, Xie P, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin P, Nelkin E (2003) The version 2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J Hydrometeorol 4:1147–1167
Alkama R, Decharme B, Douville E, Becker M, Cazenave A, Sheffield J, Voldoire A, Tyteca S, Lemoigne P (2010) Global evaluation of the ISBA-TRIP continental hydrological system. Part 1: a twofold constraint using GRACE terrestrial water storage estimates and in situ River discharges. J Hydrometeorol 11:583–600
Amman CM, Joos F, Schimel DS, Otto-Bliesner BL, Tomas RA (2007) Solar influence on climate during the past millemnium: results from transient simulations with the NCAR climate system model. Proc Natl Acad Sci 104:3713–3718
Antonov JI, Locarnini RA, Boyer TP, Mishonov AV, Garcia HE (2006) World Ocean Atlas 2005, volume 2: salinity. S. Levitus, Ed. NOAA Atlas NESDIS 62, US Government Printing Office, Washington, DC
Arakawa A, Lamb VR (1981) A potential enstrophy and energy conserving scheme for the shallow water equations. Mon Weather Rev 109:18–36
Arzel O, Fichefet T, Goosse H (2006) Sea ice evolution over the 20th and 21st centuries as simulated by current AOGCMs. Ocean Model 12:401–415
Axell LB (2002) Wind-driven internal waves and Langmuir circulations in a numerical ocean model of the southern Baltic Sea. J Geophys Res 107:3204. doi:10.1029/2001JC000922
Balsameda M, Mogensen K, Molteni F, Weaver AT (2010) The NEMOVAR-COMBINE ocean reanalysis, COMBINE technical report no 1, (http://www.combine-project.eu/Technical-Reports.1668.0.html)
Baringer MO, Larsen JC (2001) Sixteen years of Florida current transport at 27°N. Geophys Res Lett 28:3179–3182
Barnier B, Madec G, Penduff T, Molines J-M, Treguier A-M, Le Sommer J, Beckmann A, Biastoch A, Böning C, Dengg J, Derval C, Durand E, Gulev S, Remy E, Talandier C, Theetten S, Maltrud M, McClean J, De Cuevas B (2006) Impact of partial steps and momentum advection schemes in a global ocean circulation model at eddy-permitting resolution. Ocean Dyn 56:543–567
Beckmann A, Döscher R (1997) A method for improved representation of dense water spreading over topography in geopotential-coordinate models. J Phys Oceanogr 27:581–591
Belamari S (2005) Report on uncertainty estimates of an optimal bulk formulation for surface turbulent fluxes. MERSEA IP deliverable, D.4.1.2, 29
Bellucci A, Gualdi S, Navarra A (2010) The double-ITCZ syndrome in coupled general circulation models: the role of large-scale vertical circulation regimes. J Clim 23(5):1127–1145. doi:10.1175/2009JCLI3002.1
Best MJ, Beljaars A, Polcher J, Viterbo P (2004) A proposed structure for coupling tiled surfaces with the planetary boundary layer. J Hydrometeorol 5:1271–1278
Blanke B, Delecluse P (1993) Variability of the tropical Atlantic Ocean simulated by a general circulation model with two different mixed-layer physics. J Phys Oceanogr 23:1363–1388
Boone A, Calvet J-C, Noilhan J (1999) Inclusion of a third soil layer in a land-surface scheme using the force—restore method. J Appl Meteorol 38:1611–1630
Boone A, Masson V, Meyers T, Noilhan J (2000) The influence of the inclusion of soil freezing on simulation by a soil-atmosphere transfer scheme. J Appl Meteorol 9:1544–1569
Bougeault P (1981) Modeling the trade-wind cumulus boundary-layer. Part I: testing the ensemble cloud relations against numerical data. J Atmos Sci 38:2414–2428
Bougeault P (1982) Cloud ensemble relations based on the gamma probability distribution for the higher-order models of the planetary boundary layer. J Atmos Sci 39:2691–2700
Bougeault P (1985) A simple parameterization of the large-scale effects of cumulus convection. Mon Weather Rev 113:2108–2121
Brodeau L, Barnier B, Treguier AM, Penduff T, Gulev S (2009) An ERA40-based atmospheric forcing for global ocean circulation models. Ocean Mod 31:88–104. doi:10.1016/j.ocemod.2009.10.005
Brohan P, Kennedy JJ, Harris I, Tett SFB, Jones PD (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. J Geophys Res 111:D12106. doi:10.1029/2005JD006548
Burchard H (2002) Energy-conserving discretisation of turbulent shear and buoyancy production. Ocean Mod 4:347–361
Caballero R (2008) Hadley cell bias in climate models linked to extratropical eddy stress. Geophys Res Lett 35:L18709. doi:10.1029/2008GL035084
Calvet J-C et al (1999) MUREX: a land-surface field experiment to study the annual cycle of the energy and water budgets. Ann Geophysicae 17:838–854
Cariolle D, Teyssèdre H (2007) A revised linear ozone photochemistry parameterization for use in transport and general circulation models: multi-annual simulations. Atmos Chem Phys 7:2183–2196
Cattiaux J, Douville H, Ribes A, Chauvin F, Planté C (2012) Towards a better understanding of changes in wintertime cold extremes over Europe: a pilot study with CNRM & IPSL atmospheric models (this issue)
Chapman WL, Walsh JE (2007) Simulations of arctic temperature and pressure by global coupled models. J Clim 20(4):609–632
Church JA, White NJ (2006) A 20th century acceleration in global sea-level rise. Geophys Res Lett 33:L01602. doi:10.1029/2005GL024826
Clarke RA (1984) Transport through the Cape Farewell-Flemish Cap section. Rapp Pv Reun Cons Int Explor Met 185:120–130
Cox GFN, Weeks WF (1988) Numerical simulations of the profile properties of undeformed first-year sea ice during the growth season. J Geophys Res 93(C10):12449–12460. doi:10.1029/JC093iC10p12449
Cravatte S, Madec G, Izumo T, Menkes C, Bozec A (2007) Progress in the 3-D circulation of the eastern equatorial Pacific in a climate ocean model. Ocean Mod 17(1):28–48
Cunningham SA, Alderson SG, King BA, Brandon MA (2003) Transport and variability of the antarctic circumpolar current in the Drake Passage. J Geophys Res 108:8084. doi:10.1029/2001JC001147
Cunningham SA, Kanzow TO, Rayner D, Baringer MO, Johns WE, Marotzke J, Longworth HR, Grant EM, Hirschi JJ-M, Beal LM, Meinen CS, Bryden HL (2007) Temporal variability of the Atlantic Meridional Overturning Circulation at 26.5°N. Science 317:935–938
Curry JA (2001) INTRODUCTION to special section: FIRE Arctic clouds experiment. J Geophys Res 106:14985–14987
de Boyer Montégut C, Madec G, Fischer AS, Lazar A, Iudicone D (2004) Mixed layer depth over the global ocean: an examination of profile data and a profile-based climatology. J Geophys Res 109:C12003. doi:10.1029/2004JC002378
de Jong MF, Drijfhout SS, Hazeleger W, van Aken HM, Severijns CA (2009) Simulations of hydrographic properties in the northwestern North Atlantic Ocean in Coupled Climate Models. J Clim 22(7):1767–1786. doi:10.1175/2008JCLI2448.1
de Szoeke SP, Xie S-P (2008) The tropical eastern Pacific seasonal cycle: assessment of errors and mechanisms in IPCC AR4 coupled ocean-atmosphere general circulation models. J Clim 21(11):2573–2590
Deardoff JW (1977) A parameterization of ground-surface moisture content for use in atmospheric prediction models. J Appl Meteorol 16:1182–1185
Decharme B, Douville H (2006) Introduction of a sub-grid hydrology in the ISBA land surface model. Clim Dyn 26:65–78
Decharme B, Douville H (2007) Global validation of the ISBA sub-grid hydrology. Clim Dyn 29:21–37
Decharme B, Douville H, Boone A, Habets F, Noilhan J (2006) Impact of an exponential profile of saturated hydraulic conductivity within the ISBA LSM: simulations over the Rhine basin. J Hydrometeorol 7:61–80
Decharme B, Alkama R, Douville E, Becker M, Cazenave A (2010) Global evaluation of the ISBA-TRIP continental hydrologic system. Part 2: uncertainties in river routing simulation related to flow velocity and groundwater storage. J Hydrometeorol 11:601–617
Decharme B, Boone A, Delire C, Noilhan J (2011a) Local evaluation of the ISBA soil multilayer diffusion scheme using four pedotransfert functions. J Geophy Res (under review)
Decharme B, Alkama R, Papa F, Faroux S, Douville H, Prigent C (2011b) Global off-line evaluation of the ISBA-TRIP flood model. Clim Dyn. doi:10.1007/s00382-011-1054-9 (online)
Déqué M, Dreveton C, Braun A, Cariolle D (1994) The ARPEGE-IFS atmosphere model: a contribution to the French community climate modelling. Clim Dyn 10:249–266
Douville H, Royer J-F, Mahfouf J-F (1995) A new snow parameterization for the Météo-France climate model. Part 1: validation in stand-alone experiments. Clim Dyn 12:21–35
Emile-Geay J, Madec G (2009) Geothermal heating, diapycnal mixing and the abyssal circulation. Ocean Sci 5:281–325. doi:10.5194/os-5-203-2009
Fahrbach E, Meincke J, Østerhus S, Rohardt G, Schauer U, Tverberg V, Verduin J (2001) Direct measurements of heat and mass transports through the Fram Strait. Polar Res 20:217–224
FAO/IIASA/ISRIC/ISSCAS/JRC (2009) Harmonized world soil database (version 1.1). FAO, Rome, Italy and IIASA, Laxenburg, Austria (http://www.iiasa.ac.at/research/LUC/External-World-Soil6database/HTML/)
Fasullo JT, Trenberth KE (2008) The annual cycle of the energy budget. Part II: Meridional structures and poleward transports. J Clim 21:2313–2325
Fetterer F, Knowles K, Meier W, Savoie M (2002) Sea Ice Index. National Snow and Ice Data Center. Digital media, Boulder, CO (updated 2007)
Flato GM, Brown RD (1996) Variability and climate sensitivity of landfast Arctic sea ice. J Geophys Res 101(C1):25767–25777. doi:10.1029/96JC02431
Fouquart Y, Bonnel B (1980) Computations of solar heating of the earth’s atmosphere: a new parametrization. Beitr Phys Atmos 53:35–62
Franco B, Fettweis X, Erpicum M, Nicolay S (2011) Present and future climates of the Greenland ice sheet according to the IPCC AR4 models. Clim Dyn 36:1897–1918. doi:10.1007/s00382-010-0779-1
Galperin B, Kantha LH, Hassid S, Rosati A (1988) A quasi-equilibrium turbulent energy for geophysical flows. J Atmos Sci 45:55–62
Gent PR, McWilliams JC (1990) Isopycnal mixing in ocean circulation models. J Phys Oceanogr 20:150–155
Geoffroy O, Saint-Martin D, Voldoire A, Salas y Mélia D (2011) Climate sensitivity and radiative feedbacks in the CNRM-CM5.1 climate model. Clim Dyn (submitted)
Gordon AL (2001) Interocean exchange. In: Siedler G, Church J, Gould J (eds) Ocean circulation and climate. Academic Press, pp 303–314
Griffies SM et al (2009) Coordinated ocean-ice experiments (COREs). Ocean Mod 26:1–46. doi:10.1016/j.ocemod.2008.08.007
Guémas V, Salas-Mélia D (2008) Simulation of the Atlantic Meridional Overturning Circulation in an Atmosphere-Ocean Global Coupled Model. Part I: a mechanism governing the variability of ocean convection in a preindustrial experiment. Clim Dyn 31:29–48. doi:10.1007/s00382-007-0336-8
Habets F, Noilhan J, Golaz C, Goutorbe JP, Lacarrère P, Leblois E, Ledoux E, Martin E, Ottlé C, Vidal-madjar D (1999) The ISBA surface scheme in a macroscale hydrological model applied to the HAPEX-MOBILHY area. Part I: model and database. J Hydrol 217:75–96
Hansen B, Osterhus S (2000) North Atlantic-Nordic Seas exchanges. Prog Oceanogr 45:109–208
Hewitt HT, Copsey D, Culverwell ID, Harris CM, Hill RSR, Keen AB, McLaren AJ, Hunke EC (2011) Design and implementation of the infrastructure of HadGEM3: the next-generation Met Office climate modelling system. Geosci Model Dev 4:223–253. doi:10.5194/gmd-4-223-2011
Hortal M, Simmons AJ (1991) Use of reduced Gaussian grids in spectral models. Mon Weather Rev 119:1057–1074
Hunke EC, Dukowicz JK (1997) An elastic-viscous-plastic model for sea ice dynamics. J Phys Oceanogr 27:1849–1867
Hunke EC, Lipscomb WH (2002) CICE: the Los Alamos sea ice model, documentation and software user’s manual. T-3 fluid dynamics group, Los Alamos national laboratory, technical report LACC-98-16 v.3
Imawaki S, Uchida H, Ichikawa H, Fukasawa M, Umatani S, the ASUKA Group (2001) Satellite altimeter monitoring the Kuroshio transport south of Japan. Geophys Res Lett 28:17–20
Ingleby B, Huddleston M (2007) Quality control of ocean temperature and salinity profiles—historical and real-time data. J Mar Syst 65:158–175. doi:10.1016/j.jmarsys.2005.11.019
Intergovernmental Panel on Climate Change (2007) Climate change 2007: the physical science basis. In: Solomon S et al. (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Jones PW (1999) Conservative remapping: first- and second-order conservative remapping. Mon Weather Rev 127:2204–2210
Jones PW (2001) A user’s guide for SCRIP: a spherical coordinate remapping and interpolation package. http://climate.lanl.gov/Software/SCRIP/SCRIPusers.pdf
Kamala K, Peings Y, Terray P, Douville H (2012) ENSO-Indian monsoon teleconnection in the CNRM and IPSL historical simulations (this issue)
Kessler E (1969) On distribution and continuity of water substance in atmospheric circulations. Meteorol Monogr 10(32):88
Koch-Larrouy A, Madec G, Bouruet-Aubertot P, Gerkema T, Bessières L, Molcard R (2007) On the transformation of Pacific Water into Indonesian throughflow water by internal tidal mixing. Geophys Res Lett 34:L04604. doi:10.1029/2006GL028405
Koch-Larrouy A, Lengaigne M, Terray P, Madec G, Masson M (2010) Tidal mixing in the Indonesian Seas and its effect on the tropical climate system. Clim Dyn 34(6):891–904. doi:10.1007/s00382-009-0642-4
Kwok R, Cunningham GF, Pang SS (2004) Fram Strait sea ice outflow. J Geophys Res 109:C01009. doi:10.1029/2003JC001785
Lauer A, Hamilton K, Wang Y, Philipps VTJ, Bennartz R (2010) The impact of global warming on marine boundary layer clouds over the eastern Pacific—a regional model study. J Clim 23:5844–5863. doi:10.1175/2010JCLI3666.1
Le Sommer J, Penduff T, Theetten S, Madec G, Barnier B (2009) How momentum advection schemes affect current-topography interactions at eddy permitting resolution. Ocean Mod 29(1):1–14. doi:10.1016/j.ocemod.2008.11.007
Lenderink G, Holtslag M (2004) An updated length-scale formulation for turbulent mixing in clear and cloudy boundary layers. Q J R Meteorol Soc 130:3405–3427
Lengaigne M, Menkes C, Aumont O, Gorgues T, Bopp L, André J-M, Madec G (2007) Bio-physical feedbacks on the tropical Pacific climate in a Coupled General Circulation Model. Clim Dyn 28:503–516
Lévy M, Estubier A, Madec G (2001) Choice of an advection scheme for biogeochemical models. Geophys Res Lett 28(19):3725–3728
Li J-LF, Waliser D, Woods C, Teixeira J, Bacmeister J, Chern J, Shen B-W, Tompkins A, Tao W-K, Köhler M (2008) Comparisons of satellites liquid water estimates to ECMWF and GMAO analyses, 20th century IPCC AR4 climate simulations, and GCM simulations. Geophys Res Lett 35:L19710. doi:10.1029/2008GL035427
Lin JL (2007) The double-ITCZ problem in IPCC AR4 coupled GCMs: ocean-atmosphere feedback analysis. J Clim 20(18):4497–4525
Liu J, Zhang Z, Hu Y, Chen L, Dai Y, Ren X (2008) Assessment of surface air temperature over the Arctic Ocean in reanalysis and IPCC AR4 model simulations with IABP/POLES observations. J Geophys Res 113:D10105. doi:10.1029/2007JD009380
Locarnini RA, Mishonov AV, Antonov JI, Boyer TP, Garcia HE (2006) World Ocean Atlas 2005, volume 1: temperature. S. Levitus, Ed. NOAA Atlas NESDIS 61, U.S. Government Printing Office, Washington, DC
Louis JF (1979) A parametric model of vertical eddy fluxes in the atmosphere. Bound Layer Meteorol 17:187–202
Lucarini V, Ragone F (2011) Energetics of PCMDI/CMIP3 climate models: energy budget and meridional enthalpy transport. Rev Geophys 49:RG1001. doi:10.1029/2009RG000323
Macrander A, Send U, Valdimarsson H, Jonsson S, Käse RH (2005) Interannual changes in the overflow from the Nordic Seas into the Atlantic Ocean through Denmark Strait. Geophys Res Lett 32. doi:10.1029/2004GL021463
Madec G (2008): NEMO ocean engine. Note du Pole de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No 27 ISSN No 1288–1619
Madec G, Imbard M (1996) A global ocean mesh to overcome the North Pole singularity. Clim Dyn 12:381–388
Madec G, Delecluse P, Imbard M, Lévy C (1998) OPA 8.1 Ocean general circulation model reference manual. Note du Pôle de modélisation, Institut Pierre-Simon Laplace, no 11, 91 pp
Maisonnave E, Terray L (2008) Runoff: couplage conservatif par anomalie, technical report TR/CMGC/08/71, CERFACS, Toulouse, France. http://www.cerfacs.fr/globc/publication/technicalreport/2008/TR_runoffs.pdf
Marsaleix P, Auclair F, Floor JW, Herrmann MJ, Estournel C, Pairaud I, Ulses C (2008) Energy conservation issues in sigma-coordinate free-surface ocean models. Ocean Mod 20(1):61–89. doi:10.1016/j.ocemod.2007.07.005
Masson V, Champeaux J-L, Chauvin C, Meriguet C, Lacaze R (2003) A global database of land surface parameters at 1 km resolution for use in meteorological and climate models. J Clim 16:1261–1282
Mellor GL (1977) The gaussian cloud model relations. J Atmos Sci 34:356–358
Mellor G, Blumberg A (2004) Wave breaking and ocean surface layer thermal response. J Phys Oceanogr 34(3):693–698. doi:10.1175/2517.1
Mellor GL, Yamada T (1974) A hierarchy of turbulence closure models for planetary boundary layers. J Atmos Sci 31:1791–1806
Mellor GL, Yamada T (1982) Development of a tubulence closure model for geophysical fluid problems. Rev Geophys Space Phys 20(4):851–875
Merryfield WJ, Holloway G, Gargett AE (1999) A global ocean model with double-diffusive mixing. J Phys Oceanogr 29(6):1124–1142
Mitchell TD, Jones PD (2005) An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int J Clim 25:693–712. doi:10.1002/joc.1181
Mlawer EJ, Taubman SJ, Brown PD, Iacono MJ, Clough SA (1997) Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J Geophys Res 102:16663–16682
Noilhan J, Mahfouf J-F (1996) The ISBA land surface parameterisation scheme. Global Planet Change 13:145–159
Noilhan J, Planton S (1989) A simple parameterization of land surface processes for meteorological models. Mon Weather Rev 117:536–549
Oki T, Sud YC (1998) Design of total runoff integrating pathways (TRIP). A global river channel network. Earth Interact 2:1–36
Ono N (1967) Specific heat and heat of fusion of sea ice. In: Oura H (ed) Physics of snow and ice, vol 1. Institute of Low Temperature Science, Hokkaido, pp 599–610
Penduff T, Le Sommer J, Barnier B, Treguier A-M, Molines J-M, Madec G (2007) Influence of numerical schemes on current-topography interactions in 1/4° global ocean simulations. Ocean Sci 3(4):491–528
Penduff T, Juza M, Brodeau L, Smith GC, Barnier B, Molines J-M, Treguier A-M, Madec G (2010) Impact of global ocean model resolution on sea-level variability with emphasis on interannual time scales. Ocean Sci 6(1):269–284
Polcher J, McAvaney B, Viterbo P, Gaertner M-A, Hahmann A, Mahfouf J-F, Noilhan J, Phillips T, Pitman A, Schlosser CA, Schulz J-P, Timbal B, Verseghy D, Xue Y (1998) A proposal for a general interface between land-surface schemes and general circulation models. Global Planet Change 19:261–276
Pringle DJ, Eicken H, Trodahl HJ, Backstrom LGE (2007) Thermal conductivity of landfast Antarctic and Arctic sea ice. J Geophys Res 112:C04017. doi:10.1029/2006JC003641
Quaas J, Boucher O (2005) Constraining the first aerosol indirect radiative forcing in the LMDZ GCM using POLDER and MODIS satellite data. Geophys Res Lett 32:L17814. doi:10.1029/2005GL023850
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14). doi:10.1029/2002JD002670
Rayner NA, Brohan P, Parker DE, Folland CK, Kennedy JJ, Vanicek M, Ansell T, Tett SFB (2006) Improved analyses of changes and uncertainties in marine temperature measured in situ since the mid-nineteenth century: the HadSST2 dataset. J Clim 19:446–469
Ricard JL, Royer JF (1993) A statistical cloud scheme for use in an AGCM. Ann Geophys 11:1095–1115
Rossow WB, Walker AW, Beuschel DE, Roiter MD (1996) International satellite cloud climatology project (ISCCP) documentation of new cloud datasets. WMO/TD-No. 737, World Meteorological Organization, 115 pp
Roullet G, Madec G (2000) Salt conservation, free surface and varying volume: a new formulation for ocean GCMs. J Geophys Res 105:23927–23942
Russell JL, Stouffer RJ, Dixon KW (2006) Intercomparison of the Southern Ocean circulations in IPCC coupled model control simulations. J Clim 19:4560–4575
Salas y Mélia D (2002) A global coupled sea ice-ocean model. Ocean Model 4:137–172
Salas y Mélia D, Chevallier M (2012) The impact of the inclusion of new sea ice processes on the simulation of sea ice by CNRM-CM5 global coupled model. Clim Dyn (submitted)
Schmidt GA, Bitz CM, Mikolajewicz U, Tremblay L-B (2004) Ice-ocean boundary conditions for coupled models. Ocean Model 7:59–74. doi:10.1016/S1463-5003(03)00030-1
Schott FA, Lee TN, Zantopp R (1988) Variability of Structure and Transport of the Florida Current in the Period Range of Days to Seasonal. J Phys Oceanogr 9:1209–1230
Schulz M (2007) Constraining model estimates of the aerosol radiative forcing. Habilitation thesis, Université Pierre et Marie Curie
Schweiger A, Lindsay R, Zhang J, Steele M, Stern H (2011) Uncertainty in modeled arctic sea ice volume. J Geophys Res 116:C00D06. doi:10.1029/2011JC007084
Shaffrey LC, Stevens I, Norton WA, Roberts MJ, Vidale PL, Harle JD, Jrrar A, Steven DP, Woodage MJ, Demory ME, Donners J, Clark DB, Clayton A, Cole JW, Wilson SS, Connolley WM, Davies TM, Iwi AM, Johns TC, King JC, New AL, Slingo JM, Slingo A, Steenman-Clark L, Martin GM (2009) UK HiGEM: the New UK high-resolution global environment model—model description and basic evaluation. J Clim 22:1861–1896. doi:10.1175/2008JCLI2508.1
Simmons HL, Jayne SR, St. Laurent LC, Weaver AJ (2004) Tidally driven mixing in a numerical model of the ocean general circulation. Ocean Mod 6(3–4):245–263. doi:10.1016/S1463-5003(03)00011-8
Smith R (1990) A scheme for predicting layer clouds and their water content in a general circulation model. Q J R Meteorol Soc 116:435–460
SPARC CCMVal (2010) SPARC CCMVal Report on the Evaluation of chemistry-climate models. In: Eyring V, Shepherd TG, Waugh DW (eds) SPARC report no. 5, WCRP132, WMO/TD-No. 1526, http://www.atmosp.physics.utoronto.ca/SPARC
Szopa S, Cozic A, Shulz M, Balkanski Y, Hauglustaine D (2012) Aerosol and ozone changes as forcing for climate evolution between 1850 and 2100 (this issue)
Tanaka HL, Ishizaki N, Nohara D (2005) Intercomparison of the intensities and trends of Hadley, walker and monsoon circulations in the global warming projections. SOLA 1:77–80. doi:10.2151/sola.2005-021
Taylor KE (2001) Summarizing multiple aspects of model performance in single diagram. J Geophys Res 106(D7):7183–7192
Taylor KE, Stouffer RJ, Meehl G (2009) A summary of the CMIP5 experiment design. Available at http://cmip-pcmdi.llnl.gov/cmip5//
Tegen I, Hollrig P, Chin M, Fung I, Jacob D, Penner J (1997) Contribution of different aerosol species to the global aerosol extinction optical thickness: estimates from model results. J Geophys Res 102:23895–23915. doi:10.1029/97JD01864
Thorndike AS, Rothrock DS, Maykut GA, Colony R (1975) The thickness distribution of sea ice. J Geophys Res 80:4501–4513
Trenberth KE, Caron JM (2001) Estimates of meridional atmosphere and ocean heat transports. J Clim 14:3433–3443
Trenberth KE, Stepaniak DP (2001) Indices of El Niño evolution. J Clim 14:1697–1701
Trenberth KE, Fasullo JT, Kiehl J (2009) Earth global energy budget. Bull Am Meteorol Soc 90:311–323
Uppala SM et al (2006) The ERA-40 re-analysis. Q J R Meteorol Soc 131:2961–3012
Valcke S (2006) OASIS3 user guide (prism_2-5). Technical report TR/CMGC/06/73, CERFACS, Toulouse, France, 60 pp
Vancoppenolle M, Fichefet T, Goosse H, Bouillon S, Madec G, Morales Maqueda MA (2009) Simulating the mass balance and salinity of Arctic and Antarctic sea ice. 1. Model description and validation. Ocean Model 27:33–53. doi:10.1016/j.ocemod.2008.10.005
Waliser D, Seo K-W, Schubert S, Njoku E (2007) Global water cycle agreement in the climate models assessed in the IPCC AR4. Geophys Res Lett 34:L16705. doi:10.1029/2007GL030675
Walsh JE, Chapman WL, Romanovsky V, Christensen JH, Stendel M (2008) Global climate model performance over Alaska and Greenland. J Clim 21(23):6156–6174
Weill A, Eymard L, Caniaux G, Hauser D, Planton S, Dupuis H, Brut A, Guerin C, Nacass P, Butet A, Cloché S, Pedreros R, Durand P, Bourras D, Giordani H, Lachaud G, Bouhours G (2003) Toward a better determination of turbulent air-sea fluxes from several experiments. J Clim 16:600–618
Wielicki BA, Priestley K, Minnis P, Loeb N, Kratz D, Charlock T, Doelling D, Young D (2006) CERES radiation budget accuracy overview. 12th Conference on atmospheric radiation. Madison, Wisconsin
Woodgate RA, Aagaard K, Weingartner T (2005) Monthly temperature, salinity and transport variability of the bering strait through flow. Geophys Res Lett 32:56. doi:10.1029/2004GL021880
Worby AP, Geiger CA, Paget MJ, Van Woert ML, Ackley SF, DeLiberty TL (2008) The thickness distribution of Antarctic sea ice. J Geophys Res 113:C05S92. doi:10.1029/2007JC004254
Yamada T, Mellor GL (1975) A simulation of the Wangara atmospheric boundary layer data. J Atmos Sci 32:2309–2329
Yu L, Weller RA (2007) Objectively analyzed air-sea heat fluxes (OAFlux) for the global oceans. Bull Am Meteorol Soc 88:527–539
Acknowledgments
This work was funded by the European Commission’s 7th Framework Programme, under Grant Agreement number 226520, COMBINE project. This work was also supported by Météo-France, CNRS and Cerfacs. Supercomputing time was provided by Meteo-France/DSI supercomputing center. We gratefully acknowledge this long-term support. Figures have been done using the NCL and CDAT graphic packages.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is a contribution to the special issue on the IPSL and CNRM global climate and Earth System Models, both developed in France and contributing to the 5th coupled model intercomparison project.
Appendix: Coupling fields
Appendix: Coupling fields
-
1.
From ARPEGE atmospheric component to SURFEX surface component:
-
atmospheric forcing:
-
1.1
air temperature at forcing level
-
1.2
specific humidity at forcing level
-
1.3
wind components at forcing level
-
1.4
pressure at forcing level
-
1.5
surface pressure
-
1.6
dry air density at forcing level
-
1.7
height of model interlayers
-
1.8
orography of atmospheric model
-
1.9
cosine of zenithal angle at t
-
1.10
cosine of zenithal angle at t + 1
-
1.11
liquid precipitation surface flux
-
1.12
snow precipitation surface flux
-
1.1
-
radiative forcing:
-
1.13
solar spectral bands
-
1.14
surface downward longwave radiation
-
1.15
surface downward diffuse solar radiation for each spectral band
-
1.16
surface downward direct solar radiation for each spectral band
-
1.13
-
-
2.
From SURFEX surface component to ARPEGE atmospheric component:
-
surface fluxes:
-
2.1
surface fluxes of horizontal momentum in x and y directions
-
2.2
sensible heat flux at surface level
-
2.3
surface latent heat flux
-
2.4
surface flux of water vapor
-
2.1
-
radiative properties:
-
2.5
direct albedo for each spectral band
-
2.6
diffuse albedo for each spectral band
-
2.7
surface emissivity
-
2.8
surface radiative temperature
-
2.5
-
diagnostics variables (usefull for the cloud scheme):
-
2.9
surface humidity
-
2.10
roughness length for momentum
-
2.9
-
-
3.
From NEMO ocean component to ARPEGE atmospheric component:
-
3.1
Sea and ice surface weighted temperature
-
3.2
Sea ice extent
-
3.3
Surface ice albedo
-
3.4
Surface zonal current
-
3.5
Surface meridional current
-
3.1
-
4.
From ARPEGE atmospheric component to NEMO ocean component:
-
4.1
Zonal wind stress
-
4.2
Meridional wind stress
-
4.3
Wind stress module
-
4.4
10 meter wind module
-
4.5
Solid precipitation
-
4.6
Liquid precipitation
-
4.7
Evaporation flux
-
4.8
Sublimation over ice
-
4.9
Total non solar heat flux
-
4.10
Total solar heat flux
-
4.11
Antarctic pseudo-calving
-
4.12
Greenland pseudo calving
-
4.1
-
5.
From ARPEGE atmospheric component to TRIP runoff component
-
5.1
Land cell reservoir overflow
-
5.1
-
6.
From TRIP runoff component to NEMO ocean component
-
6.1
Runoff at discharge coastal points
-
6.1
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Voldoire, A., Sanchez-Gomez, E., Salas y Mélia, D. et al. The CNRM-CM5.1 global climate model: description and basic evaluation. Clim Dyn 40, 2091–2121 (2013). https://doi.org/10.1007/s00382-011-1259-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-011-1259-y