1 Introduction

Interfacial transport phenomena between a porous medium and an overlying fluid layer widely exist in industrial applications and environmental processes. The transition layer, a thin layer between the free fluid and the core of the medium with a constant Darcy velocity, is recognized by a drastic decrease of the velocity magnitudes within a depth, immediately below the interface demonstrated in Fig. 1.

Fig. 1
figure 1

Velocity profile near the interface of a fluid and a porous layer made of multi-sized spheres

Full size image

The dashed line in Fig. 1 indicates the velocity profile passing through the transition zone with the upper and lower limits u int and u D as the interfacial velocity and the Darcy velocity, respectively. Note that u D is an averaged quantity, that prevails in the core of the porous domain beginning at a depth below the transition zone. The thickness of the transition layer, also known as Brinkman layer (δ) and associated interfacial conditions had differently been estimated in theoretical studies (examples are given by Kaviany 1995; Ochoa-Tapia et al. 1995; Goyeau et al. 2003; Valdes-Parada et al. 2007).

In a Hele-Shaw cell, Gupte and Advani (1997) conducted velocity measurements at the interface between a fluid layer and the adjacent fibrous medium using laser Doppler velocimetry, and concluded that the transition layer zone was in the order of channel depth. Recently, Goharzadeh et al. (2005) (hereafter referred to as GKJ), combined refractive index matching (RIM) method with particle image velocimetry (PIV) to visualize and measure the velocity field in the interfacial zone between a fluid and a porous layer made of mono-sized glass beads. Unlike some theoretical estimations of the transition layer thickness, they have shown that δ was much larger than \(\sqrt{k},\) and rather in the order of the grain diameter d leading to the relation

$$ \left(\frac{\delta}{d}\right)_{\text{mono}\hbox{-}\text{sized\;beads}}\,\equiv\,O(1). $$
(1)

A more recent experimental investigation is performed by Agelinchaab et al. (2006), who also used the RIM and PIV to measure the velocity through a model porous medium adjacent to an open flow in a two-dimensional channel. Their model consisted of circular cylindrical rods installed vertically on the bottom wall of the channel in regular square arrays. They concluded that \(\delta/\sqrt{k}\) ratio was in the order of 3.75–12.61.

In many natural situations and technical applications, however, one encounters a porous medium given as a mixture of multi-sized particles. Hence, the question of interest is what would be the Brinkman layer thickness if the mono-sized porous medium is replaced by a multi-sized one.

2 Experimental setup

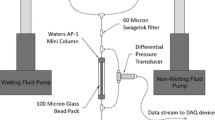
To address this question, a set-up similar to that of GKJ has been used, in which the porous layer was made of mixtures of multi-sized spherical glass beads (see Fig. 2).

Fig. 2
figure 2

Schematics of the experimental setup. A refractive-index matched oil was recirculating through and above a layer of porous medium made of multi-sized glass beads. The single-image measurements were focused in the central region of the channel, whereas the multiple images were obtained by precise moving of CCD-laser on a mobile mechanical device to cover a horizontal length of 20 < x < 30 cm

Full size image

As shown in Fig. 2, a refractive-index matched fluid is recirculating in a Plexiglas channel, filled partially by a saturated bed of multi-sized glass beads. To illuminate the region of interest, a 40 mW, 658 nm CW diode laser was mounted above the channel and operated in pulse mode. A SensiCam PCO camera (1,024 ×  1,280 pixel resolution) was installed perpendicular to the plane of the laser sheet to record the particle motion in the field of view. A lens with a focusing length of f = 50 mm was employed and connected to a 20 mm extension tube between the camera and the lens, allowing to capture a field of view of 22 × 22 mm2. All optical settings, time scales for PIV measurements, and the details of the refractive index matching was similar to those employed and reported in GKJ.

Various porous multi-sized combinations were made by mixing different numbers of glass beads with diameters of 2.5 mm (GB1), 4.6 mm (GB2) and 6.5 mm (GB3). The random arrangement of a multi-sized layer is shown in Fig. 3. The glass beads filled an identical volume of approximately V = 680 cm3 in all samples examined.

Fig. 3
figure 3

Mixture of three different sizes of glass beads with diameters 2.5, 4.6 and 6.5 mm

Full size image

Different mixture fractions were considered in terms of various number distributions of each diameter. In order to investigate the effect of number distribution on the transition layer thickness, four different fractions were chosen, and termed as SGB1, SGB2, SGB3, and EGB123. In the sample SGB1, the number density of the GB1 is superior to other glass beads. Likewise, in samples SGB2 and SGB3, the number density of GB2 and GB3 are superior to other diameters, respectively. Exception to this is sample EGB123, in which the number density of all glass bead diameters are identical. The number densities (empty bars) as well as the mass densities (black bars) for all mixture samples are illustrated in Fig. 4. In the case of SGB1 (equal mass fractions of all diameters), a high number density of 2.5 mm glass beads (GB1), corresponding to almost 83% of the total glass bead numbers was produced. The cases SGB2 and SGB3 have been selected such that each peak exactly equals the same for SGB1, leading to a symmetric change, enabling a better comparison. As far as the number density is concerned, SGB1 and SGB3 provide two extreme cases being on either side of SGB2 with a quasi-normal distribution. The procedure for exploring a possible relation between the transition layer thickness and the medium permeability or the characteristic diameter of a multi-sized porous medium is as follows: first, a characteristic diameter will be defined for multi-sized mixtures. Next, the permeability of each sample is obtained experimentally. Following this, non-invasive velocity measurements will be used to capture the thickness of the transition layer. Finally, the transition layer thickness is examined as a function of the permeability and the characteristic diameter of each mixture.

Fig. 4
figure 4

Four different number and mass distributions used in experiments. Sample (a) is a superior number density of GB1, named as SGB1. Likewise, samples (b) and (c) are termed as SGB2 and SGB3 representing superior number densities of GB2 and GB3, respectively. For comparison, sample (d) consists of equal number densities of all three glass bead diameters GB1, GB2, GB3, and is termed as EGB123

Full size image

2.1 Characteristic diameter in mixtures

A measure for defining a characteristic diameter in mixtures is provided by the moment M j (MacDonald et al. 1991), given as

$$ M_j=\sum_{i} n_i d_i^j $$
(2)

where n i is the number of glass beads in sample i with diameter d i . With known x i as the weight fraction of each size, the total mass, and glass bead densities, the moments for a multi-sized samples can be written (MacDonald et al. 1991) by the ratio of moments M 2 and M 1 given by

$$ \frac{M_2}{M_1}=\frac{\sum_{i} d_i^2n_i} {\sum_{i} d_in_i} =\frac{\sum_{i} \frac{x_i} {d_i}} {\sum_{i} \frac{x_i} {d_i^2}}\,{\hat{=}}\, d_{21}, $$
(3)

with M 1 and M 2 denoting the first and second moments of the multi-sized system, respectively.

2.2 Permeability measurements

The bulk permeability measurements for all mixture samples in the present study have been performed in an experimental device similar to that described by MacDonald et al. 1991. Compared to other measurement techniques for permeability, the one suggested by MacDonald et al. 1991 is free of artifacts. The reason is that error sources imposed by valves, tubing, and filters are corrected using a reference system with two different packing lengths L 1 and L 2. By doing so, one obtains a relation for permeability given by

$$ k=\frac{L_2-L_1}{A}\frac{\mu}{\rho g \Updelta h} \frac{Q_1Q_2} {\left(Q_1-Q_2\right)}, $$
(4)

in which ρ is the fluid density, g is the acceleration due to gravity, A is the cross section open to fluid flow, μ is the dynamic viscosity, Δh is the difference between the two fluid levels, while Q 1 and Q 2 are two volumetric flow rates. Details of the technique can be seen in the work of MacDonald et al. 1991.

3 Results

The permeability of each sample has been measured by the setup described in the previous section. The corresponding characteristic diameters of samples (d 21) have been obtained and plotted versus their permeabilities in Fig. 5 (symbols).

Fig. 5
figure 5

Permeability of all mono/multi-sized samples in terms of moments ratio. Symbols are explained in Sect. 2 and Fig. 4

Full size image

The solid line therein is a plot of the curve

$$ k=\frac{1}{180}\frac{\epsilon^3}{\left(1-\epsilon\right)^2} \left(d_{21}\right)^2, $$
(5)

which was given by MacDonald et al. 1991 by extending the Blake-Kozeny’s relation (Kaviany 1995) for mono-sized particles to a mixture. Although Hamilton (1997) proposed the relation

$$ k=\left(\frac{1} {12}\right)\left(\frac{3\left(1-\epsilon\right)^{5/3}-3\left(1- \epsilon\right)^{1/3}- 2\left(1-\epsilon\right)^2+2} {\left(1-\epsilon\right)\left[2\left(1- \epsilon\right)^{5/3}+3\right]}\right) \left(\frac{\sum_{i} \frac{x_i}{d_i}} {\sum_{i} \frac{x_i} {d_i^3}}\right) $$
(6)

He mentioned that relations (5) and (6) are similar for porosities close to 0.4, which is exactly the case in the mixture samples studied here.

As shown in Fig. 5, the bulk permeability increases from fine to course mixtures. The permeability of equal number distribution, EGB123, is closer to permeability of mono-sized medium system, GB2, and superior medium bead-size, SGB2.

To obtain the velocity profile and the transition layer thickness, PIV measurements were performed for all mono-sized as well as multi-sized samples. The randomly-packed porous sample occupied the total volume of 34 × 4 × 5 cm3 from a rectangular channel of dimensions x ch = 50 cm, y ch = 10 cm, z ch = 5 cm. In all experiments, the height of the porous and fluid layers were kept constant and equal to H p = H f = 4 cm, respectively. The Reynolds number was defined by

$$ Re_{\rm f}=\frac{u_{\hbox {max}}H_{\hbox {f}}}{\nu}, $$
(7)

and was set equal to 21 in all experiments. In Eq. 7, u max is the maximum flow velocity at the fluid surface in the x direction, and ν is the kinematic viscosity of the fluid. The results of the velocity measurements for mono-sized beads (GB1, GB2 and GB3) as well as the multi-sized mixtures (SGB1, SGB2, and SGB3) are shown in Fig. 6a and b in the dimensional and non-dimensional plane, respectively. To non-dimensionalize depth and the velocities, we have used δ and u int of each sample, respectively. As can be seen, velocity profiles within the transition layer decay similarly for mono as well as multi-sized samples. The numerical values of the velocity data have been listed in Table 1 for future comparative studies.

Fig. 6
figure 6

Velocity profiles in the transition layer zone for mono and multi-sized systems with error bars, representatively, included for the sample SGB1 (a), and the same in non-dimensional representation (b)

Full size image
Table 1 Numerical values of the measured velocities below the interface as a function of depth
Full size table

To determine the lower bound of δ, the transition layer thickness criterion (1% deviation from the constant Darcy velocity, u D) leading to the relation u = 1.01u D at y = −δ (Neale and Nader 1974) has been used. The upper bound of δ is decided by the position of the uppermost solid matrix as suggested by Beavers and Joseph (1967).

As shown in Fig. 6a, in all mono-sized samples, the velocities and transition layer thicknesses increase with the diameter of the sample, and increase from GB1 to GB3. It is interesting to note that the velocity profiles for the mixture samples migrate toward the velocity profile of the finer mono-sized beads (with the lowest limit for that of GB1), resulting in smaller transition layer thicknesses than those for mono-sized samples.

We would like to recall that in the case of SGB1, fine-diameter beads build 83% of the total beads number used in the mixture. Hence, from the perspective of the fluid particles approaching the interface from top, fine spheres are experienced sooner than other sizes of beads. In addition, the existence of fine beads in this mixture reduces the surface roughness. Consequently, the flow strength would break down immediately by the resistance of finer beads, and the velocity profile will be forced drastically to fit to the Darcy velocity in a thinner transition layer. This explanation, which is coherent with the intuition for SGB1, does apply to the case SGB3, although here the GB3 number density is dominant. The reason is the 70% probability of residing a finer bead (GB1 or GB2) in the uppermost layer of the interface of the SGB3 sample, which can be calculated easily. Hence, we observe from all the experiments that the existence of finer beads in the interface of a mixed sample plays an important role in deciding the thickness of the transition layer (see Fig. 6a).

Considering the data presented in Fig. 6b, one can correlate the velocity profile inside the transition layer with an exponential decay of the type

$$ u-u_{\rm D}=\left(u_{\text int}-u_{\rm D}\right)e^{\lambda y/\delta}, $$
(8)

satisfying the boundary conditions at the interface (u = u int at y = 0) and the bottom (u = u D at y→−∞). Relation (8) has been computed for three different values of λ with u D, u int and δ as input, and plotted in Fig. 7a for all samples. The results therein suggest that the best prediction of the velocity decay is obtained for a λ value between 5 and 7 inside the lower and between 3 and 5 inside the upper portion of δ.

Fig. 7
figure 7

Velocity decay prediction in the transition layer zone: (a) effect of decay coefficient λ for both mono and multi-sized systems (logarithmic), (b) non logarithmic representation and comparison with experimental data

Full size image

The physical interpretation of λ can be derived when comparing it with the slip condition of Beavers and Joseph (1967) at a fluid–porous interface, given by

$$ u_{\rm int}-u_{\rm D}=\frac{\sqrt{k}}{\alpha}\frac{{\rm d}u}{{\rm d}y}|_{y^{0^+}} \quad \hbox{at}\quad y=0, $$
(9)

where, u is the velocity within the fluid-filled layer, and α is a dimensionless constant which characterizes the structure of the porous medium. As in the case of mono-sized beads (Goharzadeh et al. 2005), also for multi-sized beads taken in the present study (data in fluid layer not shown), the interfacial velocity gradient displayed a continuous behavior across the interface. It is also possible that a very weak jump in the velocity gradient becomes visible once a finer-resolution visualization is performed. With the present arrangement, however, this possible slight discontinuity falls within the uncertainty range of the measured data. Therefore, for a detailed quantification of a possible weak jump, a new experimental study is required. Hence, departing from a continuous interfacial velocity profile and equating \({\rm d}u/{\rm d}y|_{0^-}\) (taken from (8)) with \({\rm d}u/{\rm d}y|_{0^+}\) (taken from (9)), a relation for the parameter dependencies among λ, α, δ and k may be obtained by

$$ \lambda=\alpha\frac{\delta}{\sqrt{k}}. $$
(10)

However, as can be seen in both panels of Fig. 7, a single λ cannot mimic the velocity profiles within the entire transition layer. It seems that for the velocity values near the top boundary (y = 0), λ = 3 is most appropriate, while λ = 7 provides a good fit to the velocity profiles in the lower portion of the transition zone. Hence, it can be expected that there exists a depth-dependent fitting parameter, which provides a better alternative than a single constant one, and can be given as

$$ u-u_{\rm D}=\left(u_{\rm int}-u_{\rm D}\right)e^{\gamma y/\delta}, $$
(11)

with

$$ \gamma(y)=\lambda +\eta \frac{y}{\delta}, $$
(12)

in which λ satisfies the same correlation of (10). The parameters λ and η can now be obtained by inserting the conditions γ (y/δ = 0) = 3 and γ (y/δ = −1) = 7, leading to

$$ \gamma(y)=3- 4\frac{y}{\delta}. $$
(13)

The result of the new, depth-dependent γ is shown in Fig. 8, which mimics the velocity profiles better than it is done by a constant λ.

Fig. 8
figure 8

Velocity decay prediction based on Eq. 11 and comparison with experimental data

Full size image

Similar to λ, it is possible to provide a physical interpretation for γ. By rewriting the right hand side of Eq. 12 as λ(1 + η/λ · y/δ), and replacing the first λ by its value from Eq. (10), we obtain

$$ \gamma = \frac{\alpha \delta}{\sqrt{k}} \left(1+\frac{\eta}{\lambda} \frac{y}{\delta}\right). $$
(14)

Furthermore, the transition layer thickness for each sample has been plotted as a function of k 1/2 and d 21 in Fig. 9a and b, respectively. The comparison clearly reveals that for multi-sized samples, δ is in the order of d 21, and one order of magnitude larger than k 1/2. Hence, it can be suggested that for a porous sample of multi-sized beads, relation (1) can be replaced by

$$ \left( {\frac{\delta }{{d_{{21}} }}} \right)_{{{\text{multi}\hbox{-}\text{sized}}}} \equiv O(1) $$
(15)
Fig. 9
figure 9

Transition layer thickness (a) versus the root of permeability (linear fit with R 2 = 0.8), and (b) versus the characteristic diameter d 21 (linear fit with R 2 = 0.85). The comparison shows clearly that δ scales with d 21 rather than k 1/2

Full size image

Note that d 21 reduces to the diameter d in a mono-sized porous sample, making relation (15) equivalent to relation (1) for mono-sized beads. An additional interesting issue is the ratio of the transition layer thickness to the square root of the permeability. The experimentally acquired data set suggests

$$ \frac{\delta}{\sqrt{k}} \equiv 29.3, $$
(16)

which is comparable to the value \(\delta/\sqrt{k}=O(30)\) mentioned by Ochoa-Tapia and Whitaker (1995) or to the same order of magnitude resulting from Eq. 5 of Macdonald et al. 1991 with \(\epsilon\) = 0.4.

Finally, we estimated the slip coefficient α appearing in Eq. (9) from the experimental data. Upon insertion of \(\sqrt{k}\) from the permeability measurements, and du/dy as well as u int − u D from our velocity measurements, a slip parameter of α = 0.1 was obtained. This value matches with that for a porous sample made of Aloxite, given by Beavers and Joseph (1967).

4 Conclusions

Combining the refractive index-matching (RIM) technique with the particle image velocimetry (PIV), velocity profiles near the interface between a fluid layer and a porous layer made of randomly packed multi-sized beads were measured. Based on the velocity measurements, the transition layer thickness could be obtained. It was found that for the case of unidirectional flow over a layer of spherical beads of mixed diameters, the transition layer thickness δ is in the order of a characteristic diameter of the mixture, represented by the second to first moments ratio d 21. Furthermore, the velocity decay through the transition layer thickness was modeled with an exponential function. The coefficient in the exponential term was taken to be depth-dependent, and was found to be equal to \(\gamma=3-4\frac{y}{\delta}.\) In addition, by fitting a linear curve to all experimental data, it was concluded that \(\delta/\sqrt{k}=29.3\) for the multi-sized glass bead samples. Finally, using the experimental data, the slip parameter α was estimated to be equal to 0.1. Both values obtained for multi-sized porous samples were found to be consistent with those reported in the literature previously.