Abstract
Previous literature on statistical properties of interbank networks has reported various power-laws, particularly for the degree distribution (i.e., the distribution of credit links between institutions). In this paper, we revisit data for the Italian interbank network based on overnight loans recorded on the e-MID trading platform during the period 1999–2010 using both daily and quarterly aggregates. In contrast to previous reports, we find no evidence in favor of a power-law characterizing the degree distribution. Rather, the data are best described by negative Binomial distributions. For quarterly data, Weibull, Gamma, and Exponential distributions tend to provide comparable fits. We find similar results when investigating the distribution of the number of transactions, even though in this case, the tails of the quarterly variables are much fatter. The absence of power-law behavior casts doubts on previous claims that these interbank data fall into the category of scale-free networks.













Similar content being viewed by others
Notes
See Albert et al. (2000).
This is not to say these papers do not yield very useful phenomenological information about the pertinent network structures. The point here is rather that there seems to exist a convention in the network literature to produce a power-law graph without a deeper statistical analysis of this issue and also often in spite of a relatively small sample of observations that additionally impedes such a strong inference on the underlying distribution.
Since we cannot easily observe the state of a hypothesized network of interbank links at a given point in time, some data aggregation is necessary. Usually, for time-aggregated data, a link is assumed to exist between two banks, if there has been a trade at any time during the aggregation period.
This is of course only true when taking banks as consolidated entities.
Directed means that \(d_{i,j}\ne d_{j,i}\) in general. Sparse means that at any point in time, the number of links is only a small fraction of the \(N(N-1)\) possible links. Valued means that interbank claims are reported in monetary values as opposed to 1 or 0 for the presence or absence of a claim, respectively.
The vast majority of trades (roughly 95 %) is conducted in Euro.
See also the e-MID website http://www.e-mid.it/.
Note that the mean in- and out-degree are identical by definition.
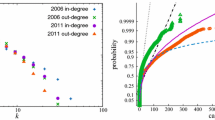
Interestingly, after standardizing the degrees, we find structural breaks in all three time series close to quarter 39, i.e., around the GFC.
Note that the first subsample roughly coincides with the dataset used by De Masi et al. (2006).
In Appendix 4, we present a similar analysis for the distribution of transaction volumes of individual institutions.
This is important, since we cannot replicate the large number of zero values that we observe in the empirical data based on these distributions. Ignoring zeros reduces the number of quarterly observations to 1,742, 3,271, and 788 for the in-variables, and 1450, 2733, and 663 for the out-variables, respectively. For the daily data, this leaves 70,584, 133,280, and 28,093 for the in-variables, and 39,619, 83,723, and 17,961 for the out-variables, respectively. The number of observations for the total degree and ntrans variables remains unaffected, since only active banks are in the sample.
There exist a number of alternative approaches in statistical extreme value theory for determining the optimal tail size. The approaches by Danielsson et al. (2001) and Drees and Kaufmann (1998) yielded results very similar to those reported in the text. We also checked certain fixed thresholds for identifying the tail region. The results remain qualitatively the same as long as the chosen upper quantile is reasonably large.
In principle, we could also use likelihood-based criteria, e.g., AIC or BIC. However, Clauset et al. (2009) provide some evidence that the KS statistic is preferable as it is more robust to statistical fluctuations.
De Masi et al. (2006) report power-law exponents between 2 and 3 for total degree, in-degree, and out-degree for daily data of our period 1 of the e-MID overnight record. Soramäki et al. (2007) also report values in this range for daily interbank payments within the U.S. Fedwire system. Boss et al. (2004) fit two power-laws to the more central and the extremal region of the in-degree distribution of monthly Austrian interbank liabilities with the extremal region exhibiting slopes of 1.73 for in-degrees and 2.01 for out-degree. This visual illustration could, however, be as well interpreted as indicating an overall exponential shape. Bech and Atalay (2010) study daily federal fund credits in the U.S. Their study constitutes a rare example of a comparative fit of a number of candidate distributions. While the overall shape of the distribution does not quite show a straight linear shape in a log–log plot, they report that the power-law gave the best fit among the candidates for out-degrees while the negative Binomial did best fit the in-degree distribution.
We have set 7 as the upper bound of the power-law parameter in our numerical ML implementation. For larger values, the evaluation of the zeta function appearing in the discrete Pareto law, cf. Appendix 2, is not accurate enough to obtain reliable estimates. The fact that the estimated values hit the upper bound quite frequently indicates that the estimated values may become even larger when increasing the upper bound.
We also generated synthetic power-law distributed random draws and estimated their scaling parameters based on the algorithm for the selection of the tail region detailed above (not reported). For the small sample sizes of the typical daily data, the tail parameter of these synthetic data is highly volatile as well, even though the very large values observed for the actual data are very rare. As usual, however, increasing the number of observations (say more than 500), typically yields estimates very close to the true parameters.
This result is driven by the higher noise level in the tail data due to a smaller number of observations compared to the complete distributions.
The stability under aggregation of power-laws characterizing the tails of iid random variables is one of the basic tenets of the statistical theory of extremes, cf. Reiss and Thomas (2007). In this sense, summing up daily power-law networks should preserve the tail index for different frequencies.
Clauset et al. (2007) show that this is necessary for datasets from the social sciences, where the maximum value is usually only a few orders of magnitude larger than the minimum, i.e., the tail is heavy but rather short. In such cases, the estimated exponents can be biased severely when using the continuous approximation.
Using a quadratic approximation of the log-likelihood at its maximum, Clauset et al. (2009) also derive an approximate closed-form solution for the estimate of \(\alpha \simeq 1 + n / \left( \sum \nolimits _{i=1}^{n} \ln \left[ \frac{x_i}{x_m - .5} \right] \right) \). This can be seen as an adjusted Hill-estimator, see Hill (1975). While we always report the exact ML estimator, we checked that the approximation is typically not too bad.
Clauset et al. (2009) also derive an (approximate) estimator for the standard error based on discrete data, which is, however, much harder to evaluate as it involves derivatives of the generalized zeta function.
Note that the maximum daily (quarterly) transaction volumes were 3.75 bn (113.46 bn) Euros for in-tvol, 4.96 bn (111.93 bn) Euros for out-tvol, and 5.32 bn (146.06 bn) Euros for total tvol, respectively. For such huge numbers, the estimation procedure, in the numerical optimization for the power-law parameters, tends to take a very long computation time. Therefore, the results in this section should be treated with care, since the rescaling might affect our statistical analysis.
References
Albert R, Jeong H, Barabasi A-L (2000) Error and attack tolerance of complex networks. Nature 406:378–482
Alderson DL, Li L (2007) Diversity of graphs with highly variable connectivity. Phys Rev E 75:046102
Anderson CW (1970) Extreme value theory for a class of discrete distributions with applications to some stochastic processes. J Appl Prob 7(1):99–113
Avnir D, Biham O, Lidar D, Malcai O (1998) Is the geometry of nature fractal? Science 279(5347):39–40
Axtell RL (2001) Zipf distribution of U.S. firm sizes. Science 293(5536):1818–1820
Beaupain R, Durré A (2012) Nonlinear liquidity adjustments in the Euro area overnight money market. Working paper series 1500, European Central Bank
Bech M, Atalay E (2010) The topology of the federal funds market. Phys A 389(22):5223–5246
Boss M, Elsinger H, Summer M, Thurner S (2004) Network topology of the interbank market. Quant Finance 4(6):677–684
Caldarelli G (2007) Scale-free networks. Oxford University Press, Oxford
Castaldi C, Dosi G (2009) The patterns of output growth of firms and countries: scale invariances and scale specificities. Empir Econ 37(3):475–495
Clauset A, Young M, Gleditsch KS (2007) On the frequency of severe terrorist events. J Confl Resolut 51(1):58–87
Clauset A, Rohilla Shalizi C, Newman MEJ (2009) Power-law distributions in empirical data. SIAM Rev 51:661–703
Cont R, Santos EB, Moussa A (2013) Network structure and systemic risk in banking systems. In: Fouque J, Langsam J (eds) Handbook of systemic risk. Cambridge University Press, Cambridge
Danielsson J, de Haan L, Peng L, de Vries C (2001) Using a bootstrap method to choose the sample fraction in tail index estimation. J Multivar Anal 76(2):226–248
De Masi G, Iori G, Caldarelli G (2006) Fitness model for the Italian interbank money market. Phys Rev E 74(6):66112
De Masi G, Gallegati M (2012) Bank-firms topology in Italy. Empir Econ 43(2):851–866
Drees H, Kaufmann E (1998) Selecting the optimal sample fraction in univariate extreme value estimation. Stoch Processes Appl 75(2):149–172
Erdös P, Renyi A (1959) On random graphs. Publ Math 6:290–297
European Central Bank (2007) Euro money market study 2006. Final report, ECB
Fagiolo G, Napoletano M, Roventini A (2008) Are output growth-rate distributions fat-tailed? Some evidence from OECD countries. J Appl Econ 23(5):639–669
Fagiolo G, Reyes J, Schiavo S (2010) The evolution of the world trade web: a weighted-network analysis. J Evolut Econ 20(4):479–514
Finger K, Fricke D, Lux T (2013) Network analysis of the e-MID overnight money market: the informational value of different aggregation levels for intrinsic dynamic processes. Comput Manag Sci 10(2–3):187–211
Fricke D, Lux T (2014) Core-periphery structure in the overnight money market: evidence from the e-MID trading platform. Comput Econ. doi:10.1007/s10614-014-9427-x
Gabaix X (1999) Zipf’s law for cities: an explanation. Q J Econ 114(3):739–767
Gai P, Haldane A, Kapadia S (2011) Complexity, concentration and contagion. J Monet Econ 58(5):453–470
Haldane AG, May RM (2011) Systemic risk in banking ecosystems. Nature 469(7330):351–355
Hill BM (1975) A simple general approach to inference about the tail of a distribution. Ann Stat 3(5):1163–1174
Ioannides YM, Loury LD (2004) Job information networks, neighborhood effects, and inequality. J Econ Lit 42(4):1056–1093
Krämer W, Runde R (1996) Stochastic properties of German stock returns. Empir Econ 21(2):281–306
Leadbetter M (1983) Extremes and local dependence in stationary sequences. Zeitschrift fuer Wahrscheinlichkeitstheorie und Verwandte Gebiete 65:291–306
Lux T (2000) On moment condition failure in German stock returns: an application of recent advances in extreme value statistics. Empir Econ 25(4):641–652
Mandelbrot B (1963) The variation of certain speculative prices. J Bus 36:394
Nier E, Yang J, Yorulmazer T, Alentorn A (2007) Network models and financial stability. J Econ Dyn Control 31(6):2033–2060
Reiss R-D, Thomas M (2007) Statistical analysis of extreme values: with applications to insurance, finance, hydrology and other fields, 3rd edn. Birkhäuser Verlag, Switzerland
Roukny T, Bersini H, Pirotte H, Caldarelli G, Battiston S (2013) Default cascades in complex networks: topology and systemic risk. Sci Rep 3(2759):1–8
Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, White DR (2009) Economic networks: the new challenges. Science 325(5939):422–425
Silverberg G, Verspagen B (2007) The size distribution of innovations revisited: an application of extreme value statistics to citation and value measures of patent significance. J Econom 139(2):318–339
Soramäki K, Bech ML, Arnold J, Glass RJ, Beyeler W (2007) The topology of interbank payment flows. Phys A 379:317–333
Stumpf MPH, Ingram PJ (2005) Probability models for degree distributions of protein interaction networks. Europhys Lett 71(1):152–158
Stumpf MPH, Ingram PJ, Nouvel I, Wiuf C (2005) Statistical model selection applied to biological network data. Proc Comput Syst Biol 3:65–73
Stumpf MPH, Wiuf C, May RM (2005) Subnets of scale-free networks are not scale-free: sampling properties of networks. Proc Natl Acad Sci USA 102(12):4221–4224
Stumpf MPH, Porter MA (2012) Critical truths about power laws. Science 335(6069):665–666
Upper C, Worms A (2004) Estimating bilateral exposures in the German interbank market: is there a danger of contagion? Cross-border bank contagion in Europe. Eur Econ Rev 48(4):827–849
Author information
Authors and Affiliations
Corresponding authors
Additional information
The article is part of a research initiative launched by the Leibniz Community. We are grateful for helpful comments by Aaron Clauset and Michael Stumpf as well as those of two anonymous reviewers. Thomas Lux also gratefully acknowledges financial support of this research from the European Union Seventh Framework Programme under Grant Agreement No. 619255 while Daniel Fricke gratefully acknowledges FP-7 support under Grant Agreement CRISIS-ICT-2011-288501.
Appendices
Appendix 1: Truncated distributions and maximum likelihood
The distribution fitting approach described in the main text involves fitting a set of candidate distributions with possibly differing support. For example, some distributions have support at zero, while others do not. Similarly, when focusing on the tail observations, we have to get rid of the probability mass below the cutoff point in order to accurately calculate the statistics. Therefore, we describe the use of truncated distributions and ML fitting in this Appendix in more detail.
1.1 Normalization
When working with truncated variables, we need to make sure to use the correct pdfs and cdfs, since the ML estimation and the evaluation of the fit (KS statistic) depend on them. In order to illustrate this issue, let variable \(x\) have the pdf \(p(x)\) with support \([0,\infty ]\). As usual, the cdf is defined as
Now, suppose the data are (left-)truncated at some value \(x_m\), i.e., the variable \(\tilde{x}\) follows the same distribution as \(x\), but the pdf has limited support \([x_m,\infty ]\) with minimum value \(x_m >0 \). For our purposes, it is therefore useful to define the quantity
or more compactly
We can properly construct the pdf of \(\tilde{x}\), say \(\tilde{p}\), as
where the denominator distributes the probability mass of \(p(x)\) among the support of \(\tilde{x}\).
For the calculation of the KS statistics, we also need the adjusted cdf. For the supported values of \(\tilde{x}\) it takes the form
or
which can be easily evaluated.
1.2 Maximum likelihood for truncated variables
Using the previous definitions, we can show that the ML estimator for left-truncated variables does not coincide with the standard estimator. The standard ML estimator, i.e., using a sample of \(n\) observations of \(x\) and denoting by \(\theta \) the vector of parameters, can be written as
or in logs
Using the definitions from above, we can show that the ML estimator for left-truncated variables differs from the one in Eq. (13). Using Eq. (9), we can write the likelihood as
where \(x\) ignores those observations smaller than \(x_m\) and the total number of observations is \(\tilde{n}\) instead of \(n\). Taking logarithms we obtain
which can be written as
The second part of this equation looks familiar, as it corresponds to Eq. (13) for the \(\tilde{n}\) observations with values \(\ge x_m\). However, the normalization term on the left does not vanish (as it depends on the parameter vector) and affects the location of the ML estimator. Therefore, we need to find the \(\theta \) that maximizes Eq. (16). The standard ML estimator would not be efficient.
Appendix 2: Discrete power-laws and parameter estimation
This presentation is mostly based on Clauset et al. (2009).
1.1 Discrete power-laws
A power-law distributed variable \(x\) obeys the pdf
where \(\alpha >0\) is the tail exponent with ‘typical’ interesting values in the range between 1 and 3. In many cases, however, the power-law only applies for some (upper) tail region, defined by the minimum value \(x_m\). While it is common to approximate discrete power-laws by the (simpler) continuous version, for our (integer-valued) data, we employ the more accurate discrete version in the paper.Footnote 23
In the discrete case, the cdf of the power-law can be written as
where
is the generalized or Hurwitz zeta function.
1.2 Estimation of \(\alpha \) and \(x_m\)
For a given lower bound \(x_m\), the ML estimator of \(\alpha \) can be found by direct numerical maximization of the log-likelihood function
where \(n\) is the number of observations.Footnote 24 For simplicity, we approximate the standard error of the estimated \(\hat{\alpha }\) (for \(\hat{\alpha }>1\)) using the closed-form solution based on continuous data.Footnote 25 Neglecting higher-order terms, this can be calculated as
However, the equations assume that \(x_m\) is known in order to obtain an accurate estimate of \(\alpha \).Footnote 26 When the data span only a few orders of magnitude, as usual in many social or complex systems, an underpopulated tail would come along with little statistical power. Therefore, we employ the numerical method proposed by Clauset et al. (2007) for selecting the \(x_m\) that yields the best power-law model for the data. To be precise, for each \(x_m\) over some reasonable range, we first estimate the scaling parameter using Eq. (20) and calculate the corresponding KS statistic between the fitted data and the theoretical distribution with the estimated parameters. The reported \(x_m\) and \(\alpha \) are those that minimize the KS statistic, i.e., minimize the distance between the observed and fitted probability distribution. According to Clauset et al. (2007, 2009), minimizing the KS statistic is generally superior to other distance measures, e.g., likelihood-based measures such as AIC or BIC.
Appendix 3: Goodness-of-fit test for the estimated distributions
Since the distribution of the KS statistics is unknown for the comparison between an empirical subsample and a hypothetical distribution with estimated parameters, we carry out a Monte Carlo approach. We sample synthetic datasets from the estimated distribution, compute the distribution of KS statistics, and compare the results to the observed value for the original dataset. If the KS statistic of the empirical dataset is beyond the \(\alpha \) percent quantile of the Monte Carlo distribution of KS values, we reject the pertinent distribution at the \(1-\alpha \) level of significance. In our results, we indicate significant fits at the 5 % confidence level using asterisks. We should stress that we carry out this (very time-consuming) GOF experiment only for the distribution with the minimum KS statistic for each sample and variable, respectively. This can be justified by the fact that, even though other candidate distributions may not be rejected as well, they are clearly inferior to the optimal distribution in terms of the KS statistic.
Appendix 4: Distributional properties of transaction volumes
Here, we report the results using another important measure for interbank networks, namely the transaction volumes (tvol). We use the same distribution fitting approach as before, differentiating between in-tvol, out-tvol, and their sum (total tvol), respectively. Figures 14 and 15 show the ccdfs for the quarterly and daily variables on a log–log scale. We should stress that the minimum trade size on the e-MID market is 50,000 Euros. In order to run our estimation procedure in a reasonable amount of time, we rescale the tvol variables by a factor of \(10^{-6}\) such that a transaction size of 50,000 is represented by a value of .05.Footnote 27 We then round the tvol variable toward the nearest integer (otherwise the discrete candidate distributions could not be accurately evaluated), again ignoring zero values. In this way, we restrict our samples to relatively large transaction volumes with at least 500,000 Euros, represented by positive integer values. Note that, besides the upward bias of the data and the fact that the data now span several orders of magnitude, it is again hard to visually detect linear decay over several orders of magnitude in the ccdfs. We should also stress that we did not perform the GOF exercise for the tvol variables, since it is too time-consuming in this case.
1.1 Daily data
Tables 9, 10, and 11 show the results for the daily data. The complete distributions are now usually fitted best by Log-normal distributions, whereas the fit of the power-law is very poor in general. The power-law parameters are again very small, with typical values around 1.22, cf. Table 10 (top, complete). For the tail observations, the best fit again is always provided by Log-normal distributions, cf. Table 11. Interestingly, the tail exponents of the daily data are within the typical range of meaningful power-laws, cf. Table 10 (top, tail), but the power-law is still not the best description of the data. In the end, for the transaction volumes, we find no evidence in favor of power-laws.
1.2 Quarterly data
Tables 12 and 13 show the results for the quarterly data. The complete in-, out-, and total degree distributions are now fit best by Weibull, negative Binomial, and Log-normal distributions, respectively. In many cases, these distributions yield comparable KS statistics, but the clear advantage of the Log-normal distribution for the daily data does not carry over to the quarterly level in all cases. Similar to the daily estimates, the power-law parameters are within the usual range of empirical power-laws. As before, however, the tails are best described by Log-normal distributions. Therefore, while the tails of the tvol variables are somewhat fatter compared to the degree and ntrans variables, the power-law remains a poor description of the data.
Rights and permissions
About this article
Cite this article
Fricke, D., Lux, T. On the distribution of links in the interbank network: evidence from the e-MID overnight money market. Empir Econ 49, 1463–1495 (2015). https://doi.org/10.1007/s00181-015-0919-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-015-0919-x