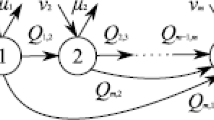Abstract
Using a modified one-dimensional model for the spread of an SIS disease on a network, we show that the behaviour of complex network simulations can be replicated with a simpler model. This model is then used to design optimal controls for use on the network, which would otherwise be unfeasible to obtain, resulting in information about how best to combine a population-level random intervention with one that is more targeted. This technique is used to minimise intervention costs over a short time interval with a target prevalence, and also to minimise prevalence with a specified budget. When applied to chlamydia, we find results consistent with previous work; that is maximising targeted control (contact tracing) is important to using resources effectively, while high-intensity bursts of population control (screening) are more effective than maintaining a high level of coverage.








Similar content being viewed by others
References
Althaus, C. L., Heijne, J. C. M., Roellin, A., & Low, N. (2010). Transmission dynamics of Chlamydia trachomatis affect the impact of screening programmes. Epidemics, 2(3), 123–131. doi:10.1016/j.epidem.2010.04.002.
Althaus, C. L., Turner, K. M. E., Schmid, B. V., Heijne, J. C., Kretzschmar, M., & Low, N. (2012). Transmission of Chlamydia trachomatis through sexual partnerships: a comparison between three individual-based models and empirical data. J. R. Soc. Interface, 9(66), 136–146. doi:10.1098/rsif.2011.0131.
Anderson, R. M., & May, R. M. (1991). Infectious diseases of humans: dynamics and control. London: Oxford University Press.
Armbruster, B., & Brandeau, M. L. (2007a). Contact tracing to control infectious disease: when enough is enough. Health Care Manage. Sci., 10(4), 341–355. doi:10.1007/s10729-007-9027-6.
Armbruster, B., & Brandeau, M. L. (2007b). Optimal mix of screening and contact tracing for endemic diseases. Math. Biosci., 209, 386–402. doi:10.1016/j.mbs.2007.02.007.
Armbruster, B., & Brandeau, M. L. (2010). Cost-effective control of chronic viral diseases: finding the optimal level of screening and contact tracing. Math. Biosci., 224, 35–42. doi:10.1016/j.mbs.2009.12.006.
Ball, F., & Neal, P. (2008). Network epidemic models with two levels of mixing. Math. Biosci., 212, 69–87. doi:10.1016/j.mbs.2008.01.001.
Banks, H. T., Kwon, H.-D., Toivanen, J. A., & Tran, H. T. (2006). A state-dependent Riccati equation-based estimator approach for HIV feedback control. Optim. Control Appl. Methods, 27(2), 93–121.
Barabasi, A.-L., Albert, R., & Jeong, H. (1999). Mean-field theory for scale-free random networks. Physica A, 272(1–2), 173–187.
Bauch, C. T. (2002). A versatile ODE approximation to a network model for the spread of sexually transmitted diseases. J. Math. Biol., 45(5), 375–395. doi:10.1007/s002850200153.
Brown, V. (2010). Modelling healthcare provision for an infectious disease using optimal control. PhD thesis, University of Bath, University of Bath, Bath.
Clarke, J., White, K. A. J., & Turner, K. (2012). Exploring short-term responses to changes in the control strategy for Chlamydia trachomatis. Comput. Math. Methods Med., 2012, 803097. doi:10.1155/2012/803097.
Conn, A. R., Gould, N., Sartenaer, A., & Toint, P. L. (1996). Convergence properties of an augmented Lagrangian algorithm for optimization with a combination of general equality and linear constraints. SIAM J. Optim., 6(3), 674–703.
Dadebo, S. A., & McAuley, K. B. (1995). Dynamic optimization of constrained chemical engineering problems using dynamic programming. Comput. Chem. Eng., 19(5), 513–525. doi:10.1016/0098-1354(94)00086-4.
de Vries, R., van Bergen, J. E. A. M., de Jong-van den Berg, L. T. W., & Postma, M. J. (2006). Systematic screening for Chlamydia trachomatis: estimating cost-effectiveness using dynamic modeling and Dutch data. Value Health, 9(1), 1–11. doi:10.1111/j.1524-4733.2006.00075.x.
Dorey, M. (2008). Modelling the spread of disease on networks. Ph.D. thesis, University of Bath.
Eames, K. T. D., & Keeling, M. J. (2002). Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl. Acad. Sci. USA, 99(20), 13330–13335. doi:10.1073/pnas.202244299.
Eames, K. T. D., & Keeling, M. J. (2003). Contact tracing and disease control. Proc. R. Soc. B, 270(1533), 2565–2571. doi:10.1098/rspb.2003.2554.
Eames, K. T. D., & Keeling, M. J. (2004). Monogamous networks and the spread of sexually transmitted diseases. Math. Biosci., 189(2), 115–130. doi:10.1016/j.mbs.2004.02.003.
Gersovitz, M., & Hammer, J. S. (2004). The economical control of infectious diseases. Econ J, 114, 1–27. doi:10.1046/j.0013-0133.2003.0174.x.
Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem., 81(25), 2340–2361. doi:10.1021/j100540a008.
Härkegård, O., & Glad, S. T. (2005). Resolving actuator redundancy–optimal control vs. control allocation. Automatica, 41(1), 137–144. doi:10.1016/j.automatica.2004.09.007.
Hethcote, H. W., & Yorke, J. A. (1984). Lecture notes in biomathematics: Vol. 66. Gonorrhea transmission dynamics and control. doi:10.1002/bimj.4710280308.
Hrovat, D. (1997). Survey of advanced suspension developments and related optimal control applications. Automatica, 33(10), 1781–1817. doi:10.1016/S0005-1098(97)00101-5.
Keeling, M. J., & Eames, K. T. D. (2005). Networks and epidemic models. J. R. Soc. Interface, 2(4), 295–307. doi:10.1098/rsif.2005.0051.
Keeling, M. J., & Rohani, P. (2008). Modeling infectious diseases in humans and animals. Princeton: Princeton University Press.
Kolda, T. G., Lewis, R. M., & Torczon, V. (2006). A generating set direct search augmented Lagrangian algorithm for optimization with a combination of general and linear constraints. Tech. rep., Sandia National Laboratories, sAND2006-5315 (August 2006).
Korobeinikov, A. (2007). Global properties of infectious disease models with nonlinear incidence. Bull. Math. Biol., 69, 1871–1886. doi:10.1007/s11538-007-9196-y.
Korobeinikov, A., & Maini, P. K. (2005). Non-linear incidence and stability of infectious disease models. Math. Med. Biol., 22, 113–128. doi:10.1093/imammb/dqi001.
Kretzschmar, M., Welte, R., van den Hoek, A., & Maarten, J. P. (2001). Comparative model-based analysis of screening programs for chlamydia trachomatis infections. Am. J. Epidemiol., 153(1), 90–101. doi:10.1093/aje/153.1.90.
Kretzschmar, M., Turner, K. M. E., Barton, P. M., Edmunds, W. J., & Low, N. (2009). Predicting the population impact of chlamydia screening programmes: comparative mathematical modelling study. Sex. Transm. Infect., 85(5), 359–366. doi:10.1136/sti.2009.036251.
Kretzschmar, M., Satterwhite, C., Leichliter, J., & Berman, S. (2012). Effects of screening and partner notification on chlamydia positivity in the United States: a modeling study. Sex. Transm. Dis., 39(5), 325–331. doi:10.1097/OLQ.0b013e31824e52c2.
Lenhart, S., & Tridane, A. (2012). The Society for Mathematical Biology annual meeting and conference, Society for Mathematical Biology. Agent-based models of biological systems: approximation and control.
Lenhart, S., & Workman, J. T. (2007). Mathematical and computational biology series. Optimal control applied to biological models. London: Chapman and Hall/CRC.
Lewis, R. M., & Torczon, V. (2002). A globally convergent augmented Lagrangian pattern search algorithm for optimization with general constraints and simple bounds. SIAM J. Optim., 12(4), 1075–1089. doi:10.1137/S1052623498339727.
Liljeros, F., Edling, C. R., Amaral, L. A. N., Stanley, H. E., & Aberg, Y. (2001). The web of human sexual contacts. Nature, 411, 907–908. doi:10.1038/35082140.
Liu, W., Levin, S. A., & Iwasa, Y. (1986). Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol., 23(2), 187–204. doi:10.1007/BF00276956.
Liu, W., Hethcote, H. W., & Levin, S. A. (1987). Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol., 25(4), 359–380. doi:10.1007/BF00277162.
Luus, R. (1992). On the application of iterative dynamic programming to singular optimal control problems. IEEE Trans. Autom. Control, 37(11), 1802–1806.
Mercer, C. H., Aicken, C. R. H., Brook, G., Estcourt, C. S., & Cassell, J. A. (2011). Estimating the likely public health impact of partner notification for a clinical service: an evidence-based algorithm. Am. J. Publ. Health, 101(11), 2117–2123. doi:10.2105/AJPH.2011.300211.
Molloy, M., & Reed, B. (1995). A critical point for random graphs with a given degree sequence. Random Struct. Algorithms, 6(2–3), 161–180. doi:10.1002/rsa.3240060204.
National Chlamydia Screening Programme (2009). The bigger picture. The National Chlamydia Screening Programme 2008/09 annual report, Tech. rep., Health Protection Agency (November 2009).
National Chlamydia Screening Steering Group (2004). First steps. Annual report of the National Chlamydia Screening Programme in England, 2003/04, Tech. rep., Department of Health (November 2004).
Pastor-Satorras, R., & Vespignani, A. (2001). Epidemic spreading in scale-free networks. Phys. Rev. Lett., 86(14), 3200–3203. doi:10.1103/PhysRevLett.86.3200.
Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V., & Mishchenko, E. F. (1962). The mathematical theory of optimal processes. New York: Wiley.
Rand, D. A. (1999). Advanced ecological theory: principles and applications (pp. 100–142). Oxford: Blackwell Science.
Robins, G., Pattison, P., & Woolcock, J. (2004). Missing data in networks: exponential random graph (p*) models for networks with non-respondents. Soc. Netw., 26(3), 257–283. doi:10.1016/j.socnet.2004.05.001.
Roy, M., & Pascual, M. (2006). On representing network heterogeneities in the incidence rate of simple epidemic models. Ecol. Complex., 3(1), 80–90. doi:10.1016/j.ecocom.2005.09.001.
Tholudur, A., & Ramirez, W. F. (1997). Obtaining smoother singular arc policies using a modified iterative dynamic programming algorithm. Int. J. Control, 68(5), 1115–1128. doi:10.1080/002071797223235.
Turner, K., Adams, E., Grant, A., Macleod, J., Bell, G., Clarke, J., & Horner, P. (2011). Costs and cost effectiveness of different strategies for chlamydia screening and partner notification: an economic and mathematical modelling study. BMJ, 342, c7250. doi:10.1136/bmj.c7250.
Volz, E. (2008). Sir dynamics in random networks with heterogeneous connectivity. J. Math. Biol., 56, 293–310.
Wächter, A., & Biegler, L. T. (2006). On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program., 106(1), 25–57. doi:10.1007/s10107-004-0559-y.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440–442. doi:10.1038/30918.
Watts, C., Zimmerman, C., Foss, A. M., Hossain, M., Cox, A., & Vickerman, P. (2010). Remodelling core group theory: the role of sustaining populations in HIV transmission. Sex. Transm. Infect. doi:10.1136/sti.2010.044602.
Zaric, G. S., & Brandeau, M. L. (2001). Optimal investment in a portfolio of HIV prevention programs. Med. Decis. Mak., 21(5), 391–408.
Acknowledgements
We thank two anonymous reviewers for their useful comments which helped improve this manuscript. Katy Turner’s funding source is NIHR PDF-2009-02-55, and James Clarke’s is a URS from the University of Bath.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Calibration of Network Using β
A method for finding β which gives the desired prevalence p target is given below. We choose α so that it is an appropriate scale for the other parameters in the simulation.
-
1.
Generate a graph matrix with the desired distribution and randomly infect 5 % of the population.
-
2.
Simulate disease spread for 3,000 days with an initial guess for β.
-
3.
Begin adjusting β according to the following:

Each successive β i is calculated 140 days after the previous, with β 0 the initial guess.
-
4.
Continue simulation for a further 32,000 days.
-
5.
Repeat steps 1–4 100 times, then use β values from final five years to give point prediction for β.
This should give a value of β which will give an average steady state prevalence, p target.
Appendix B: Annual Screening Coverage
In the results from optimisation, values for \(\hat{\gamma_{i}}\) are presented as the screening coverage that would be achieved if one screened at rate \(\hat{\gamma_{i}}\) for a whole year. In order to calculate the probability of screening an individual over the time interval [0,T] with piecewise constant screening rate \(\hat{\gamma}\), we label the time before an individual is screened as X and use that the probability density function for X is given by \(f(t; \hat{\gamma}) = \hat{\gamma} e^{-\hat{\gamma} t}\):

Appendix C: Dynamic Partner Positivities
In Sect. 3, Fig. 3 shows the probability that a partner of either a susceptible or infected individual is infected for a range steady state prevalence values, and also results from the dynamic equivalent. It is possible that these probabilities could change when the system is not at steady state. To investigate this, we sampled partner infection probabilities for different values of prevalence as the power-law system climbed from a low prevalence of around 5 % to a high prevalence of around 35 %. For each simulation, the network system was left to reach equilibrium with a low value of β (β L =0.0009), then β was increased to β H =0.0040. As the network passed through the prevalence values of interest, the partnership probabilities were calculated.
Figure 3 shows results from this method, and we see that the behaviour is similar to the steady state situation with respect to power-law behaviour of the partner positivities. A comparison of predicted parameter values is shown in Table 3, and we see that the tracing function f(I) is largely unaffected by using dynamic simulations. The infection function g(I) has slightly different values for k g and q g , but these values give a line of best fit that falls with the confidence bounds for the steady state case. One would expect g(I) to be the most affected by the changing prevalence, since as prevalence increases infection spreads to new areas of the network, and hence the probability of a susceptible being connected to infected individuals will be slightly different. Tracing is much more of a local process, and the area around infected individuals will look largely similar to the steady state case, because individuals in the area will already have been exposed to the possibility of infection.
Appendix D: Results from when k=30
Figure 9 shows optimised controls, prevalence, and incidence for when k=30. As in Sects. 3.4.1 and 3.4.3, we minimise intervention costs subject to p T =0.05, and I(T) is minimised subject to a budget of B=15.
Optimal screening coverage and tracing efficiency (a) and (d) when k=30 for power-law network parameter values, along with corresponding prevalence (b) and (e) and incidence (c) and (f). Figure (g) shows costs resulting from the ODE and simulations. Results are shown when we aim to minimise J in Eq. (6) with p T =0.05 (a)–(c), and also when we have a budget of B=15 with I(T) being minimised (d)–(f). Output from the network simulations is averaged over 100 runs. (Color figure online)
Increasing k to 30 improves optimisation results in model (3), but this does not translate to an improvement when those controls are used in network simulations. This is because rapid switching of the controls does not translate well into the stochastic setting, and if an intervention is at a high level for a short time it is more likely to be subject to stochastic effects.
Appendix E: Results from Poisson Network
We also applied our method to a network with a Poisson distribution, with results shown below. The Poisson is labelled as a ‘random’ type network because it is generated by randomly joining nodes together until the correct number of edges is reached (which depends on the mean degree τ) (Keeling and Eames 2005). The figures are arranged as follows:
-
Figure 10 shows distributions of the whole population, people testing positive through screening, and people being infected.
Fig. 10 -
Partner positivity, and hence k f , q f , k g , and q g is estimated using the data shown in Fig. 11.
Fig. 11 Probability that the partner of an S or I individual is infected at a range of values for steady state prevalence. The infection rate β is varied in order to achieve a range of values for steady state prevalence. Figure (b) on the right shows a log–log plot of (a), along with results from a linear least-squares regression. The blue line provides estimates for k g and q g , while the red line provides estimates for k f and q f . (Color figure online)
-
Validation of model (3), as in Sect. 3.3.3 is shown in Fig. 12.
Fig. 12 Comparisons between model (3) and network simulations in terms of prevalence (a), incidence (b) and number of people detected over one year at baseline (c). Output from the network simulations is averaged over 100 runs. (Color figure online)
-
Figures 13, 14, and 15 show optimisation results with k=4 and k=12. Optimisation is done based on minimising intervention costs subject to p t =0.05 (Fig. 13), minimising I(T) subject to a budget of B=15 (Fig. 14), and both of these types of minimisation when ψ max=0.5 (Fig. 15).
Fig. 13 Optimal screening coverage and tracing efficiency (a) and (d) for random network parameter values, along with corresponding prevalence (b) and (e) and incidence (c) and (f), for k=4 (a)–(c) and k=12 (d)–(f). Figure (g) shows resulting costs from the ODE and simulations. The aim is to minimise J in Eq. (6) with p T =0.05. Output from the network simulations is averaged over 100 runs. (Color figure online)
Fig. 14 Optimal screening coverage and tracing efficiency (a) and (d) for random network parameter values, along with corresponding prevalence (b) and (e) and incidence (c) and (f), for k=4 (a)–(c) and k=12 (d)–(f). Figure (g) shows resulting costs from the ODE and simulations. Controls are optimised for a budget of B=15, minimising I(T). Output from the network simulations are averaged over 100 runs. (Color figure online)
Fig. 15 Optimal screening coverage and tracing efficiency (a) and (d) with ψ max=0.5 for random network parameter values, along with corresponding prevalence (b) and (e) and incidence (c) and (f). Figure (g) shows resulting costs from the ODE and simulations. Controls are chosen to minimise (6) with unlimited budget (a)–(c) or I(T) with a budget of B=15 (d)–(f). Output from the network simulations is averaged over 100 runs. (Color figure online)
Rights and permissions
About this article
Cite this article
Clarke, J., White, K.A.J. & Turner, K. Approximating Optimal Controls for Networks when There Are Combinations of Population-Level and Targeted Measures Available: Chlamydia Infection as a Case-Study. Bull Math Biol 75, 1747–1777 (2013). https://doi.org/10.1007/s11538-013-9867-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-013-9867-9