1 Introduction

Data streams are becoming increasingly important in several domains including financial data analysis [68], sensor network monitoring [74], moving object trajectories [15, 38], web click-stream analysis [42, 48, 59], and network traffic analysis [37]. Many applications require time-series data streams to be continuously monitored in real time, and the processing and mining of data streams are attracting increasing interest. In addition to providing SQL-like support for data stream management systems (DSMS), it is crucial to detect hidden patterns that may exist in data streams, and subsequence matching is one of the key techniques for achieving this goal.

Much of the previous work on subsequence matching over data streams has focused on finding subsequences similar to a query sequence [16, 58, 72]. In this setting, one is a fixed sequence and the other is an evolving sequence. This approach works well if we have already determined the patterns we want to find. However, we consider coevolving sequences and focus on the problem of identifying common local patterns between them. That is, our goal is to automatically detect all common local patterns over data streams without a query sequence. The problem we want to solve is as follows.

Given two data streams, determine common local patterns and their periodicities taking account of time scaling.

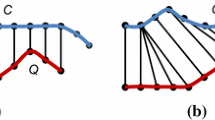
This problem is defined in detail in Sect. 3, and in Fig. 1, we present a visual intuition. The two data sets in Fig. 1a show humidity readings from two different sensors. The sensors send the readings approximately every minute. These sequences are roughly similar, but a part of the sequences is different. Intuitively, the problem is to identify the partial similarity of the sequences through data stream processing. In this example, we discover two common patterns marked with vertical lines: Subseq. #1 and #2. The matches between the two patterns are shown in Fig. 1b. The lines represent the matches between the elements of \(X\) and \(Y\) and correspond to a diagonal if the two subsequences match perfectly. We identify their similarities and matching points, that is, the starting and end positions of each sequence, in a streaming fashion, and report each match as early as possible.

Fig. 1
figure 1

Illustration of problem. Two humidity sequences have two common local patterns. Our proposed method identifies their positions and similarities in a streaming fashion

Full size image

This problem motivates us to develop the following important techniques: (1) trend detection, which is the ability to detect the most frequently occurring patterns in data streams, (2) clustering, which is the ability to find sequences that look similar and to group them, and (3) outlier detection, which is the ability to discover anomalous patterns by comparing common patterns. These exciting techniques could also provide interpretations of clusters and anomalies by annotating them in an online fashion.

In addition to the above techniques, we also consider the following interesting applications.

  • Web analysis: Web access patterns are very dynamic because of both the dynamics of web site content and structure, and the changes in the users’ interests. A continuous monitoring of web access will reveal interesting usage patterns or profiles and provide users with more suitable, customized services in real time. Webmasters may cluster users into groups based on their common characteristics for user behavioral analysis. Web site designers can use typical browsing patterns to personalize the user’s experience on the website. These groups and patterns essentially correspond to groups of common local patterns.

  • Motion capture: The recognition of human motion has been attracting intense interest in relation to computer animation, sports, and medical care. Motion data sequences are sampled many times per second and are data streams of high dimensionality. Humans never repeat exactly the same action patterns, and the actions tend to differ in terms of their duration. This appears as variability in the speed of human motion. For example, an actor may walk quickly or slowly. Such variability can manifest itself as time scaling, namely a stretching or shrinking of time-series data. Our approach aids trend detection, which can be used to identify particular movement styles for game creators, and outlier detection, which can be used by coaches to analyze athletes’ performance by identifying time-varying common motions (i.e., common local patterns).

  • Sensor network: In sensor networks, sensors send their readings frequently. Each sensor produces a stream of data, and those streams need to be monitored and combined to detect interesting changes in the environment. It is likely that users are interested in one or more sensors within a particular spatial region. These interests are expressed as trends and similar patterns, that is, common local patterns.

What similarity measures are suitable for detecting common local patterns? There are a large number of similarity measures for time-series analysis [22]. Unlike the traditional setting, data streams arrive continuously. Subsequence matching should focus on asynchronous data because streams frequently have different sampling rates. The mechanism should be robust against noise and provide scaling of the time axis. We use dynamic time warping (DTW) [9, 54] to solve this problem. DTW is a robust and widely used measure in several domains [32, 34, 45]. It is also suitable for subsequence matching since it provides time scaling (such as the stretching or shrinking of a portion of a sequence along the time axis) [4, 35, 61, 71, 75].

What are the significant challenges in terms of detecting common local patterns over data streams? Typically, DTW is applied to limited situations in an offline manner. To identify common local patterns with DTW, we have to divide data streams into all possible subsequences and compute the similarities between them because we have no advance knowledge about the patterns we are seeking. Since data streams arrive online at high bit rates and are potentially unbounded in size, the computation time and memory space increase greatly. Ideally, we need a solution that can return correct results without any omissions, even at high speeds.

Recently, the work in [65, 66] addressed the problem of finding common local patterns in data streams. Problem def0.000.-inition and its solution using DTW are introduced in [66], but the work does not provide any theoretical guarantees with respect to answer accuracy and its output overlapping results. In [65], we modified the problem definition and devised two ideas, a scoring function (Sect. 4.2.1) and a position matrix (Sect. 4.2.2). In this paper, while we share the same goals, we present a new streaming algorithm (Sect. 4.2.3), which incorporates these ideas and at the same time provides strict guarantees for our results (Sect. 4.3). By introducing a global constraint for DTW, which is suitable for stream settings, our algorithm improves the time and space requirements. Moreover, we propose enhanced solutions for different environments (Sects. 5 6) and make our algorithm more robust.

Our contributions in this paper are as follows.

  • We present CrossMatch, which can efficiently detect common local patterns in data streams. CrossMatch is a one-pass algorithm, which is strictly based on DTW and guarantees correct results.

  • In our theoretical analysis, we prove that CrossMatch does not sacrifice accuracy and detects the optimal subsequences. Moreover, we discuss the complexity in terms of computation time and memory space and show that CrossMatch significantly reduces the required amounts of these resources and achieves constant time (per update) and space.

  • For more effectiveness, we propose a sampling approach that introduces an approximation for CrossMatch. Our solution works properly for sampled sequences and achieves a significant reduction in resources.

  • As regards the accuracy and complexity for detecting common local patterns, we empirically show its usefulness on several real and synthetic data sets.

  • We address a more challenging problem of finding common local patterns in multiple data streams and show that CrossMatch can be effectively applied to this problem.

The remainder of this paper is organized as follows. Section 2 discusses related work, and Sect. 3 provides the problem definition. In Sect. 4, we describe the ideas behind CrossMatch and its algorithm, and in Sect. 5, we introduce a sampling approach for CrossMatch. Section 6 presents an enhanced algorithm for multiple streams. Section 7 reviews our experimental results, which clearly demonstrate the effectiveness of CrossMatch. Section 8 provides our conclusion.

2 Related work

Related work falls broadly into three categories: time-series similarity search, stream management, and stream mining. We review each category.

Time-series analysis and similarity search.Time-series analysis has been studied for many years. Most of the proposed methods focus on similarity queries with a query sequence. There are several distance measures for similarity queries on time-series data, for example, euclidean distance [25], DTW [9, 54], distance based on the longest common subsequence (LCSS) [67], edit distance with real penalty (EDP) [14], and edit distance on real sequence (EDR) [15]. These distance measures are selected depending on the difference of the matching strategy in application domains.

To efficiently perform the similarity search efficiently, data sequences are transformed to lower dimensional points with a dimensionality reduction technique. Agrawal et al. [2] and Faloutsos et al. [25] have utilized discrete fourier transformation (DFT) and have inserted each point into an R-tree [8]. Other reduction techniques include discrete wavelet transform (DWT) [53], singular value decomposition (SVD) [33], piecewise aggregate approximation (PAA) [70], and adaptive piecewise constant approximation (APCA) [36]. Cao et al. [10] have proposed a data reduction technique for spatio-temporal data.

Sequence matching has attracted a lot of research interest, and very successful methods have been developed for time-series data [4, 35, 61]. MDMWP [31] is a fast ranked subsequence matching solution. Ranked subsequence matching finds the top-k similar subsequences to a query sequence from data sequences. It introduces two tight lower bounds and prunes unnecessary subsequence access requests at the index level. EBSM [5] is a method for approximate subsequence matching under DTW. The key idea is to convert subsequence matching to vector matching. For the conversion, EBSM uses precomputed alignments between database sequences and query sequences. Rakthanmanon et al. [55] have focused on one trillion length time-series and several different many tens of billions time-series data and have proposed a method for searching exactly under DTW. By introducing the four optimizations based on the early stop of the computation and lower bounds, they have shown that their method is much faster than the recent search method for DTW. The above methods focus mainly on stored sequences.

As regards subsequence matching based on DTW in data streams, Zhou et al. [72] presented an efficient batch filtering method. They observe a special property of data streams, which is that successive subsequences in a stream often overlap to some extent, and improve the performance by utilizing such overlapping information as filters for lower and upper bounds. Sakurai et al. [58] presented SPRING, which efficiently monitors multiple numerical streams. They introduce two new ideas; star-padding and subsequence time warping matrix. These methods can accurately detect similar subsequences in a constant time without fixing the window size. On the other hand, Chen et al. [16] proposed an original distance function that supports shifting and scaling in both the time and amplitude dimensions and used it as a similarity measure for the efficient and continuous detection of patterns in a streaming time sequence. The above methods are powerful for dealing with problems where fixed length query sequences are given. However, they scale poorly and so are ineffective with respect to our target problem.

Regarding the detection of common local patterns over data streams, the most relevant work is Toyoda et al. [66], which proposed an algorithm for finding similar subsequences. From an algorithmic perspective, a highly relevant work is Toyoda and Sakurai [65], which presents an algorithm based on DTW. However, the algorithm in [66] does not guarantee the correctness of results and outputs subsequences with redundant information. Both algorithms are linear with regard to time and space. This paper not only overcomes the issues of accuracy and complexity, but is also more efficient in detecting common local patterns.

In the field of bioinformatics, search techniques for biological sequences have been studied and the Smith–Waterman algorithm is used to find local similarities [63]. The studies in this area focus on symbol sequences, whereas our problem focuses on numerical sequences. Our method differs in that it computes the DTW distance precisely and guarantees the detection of subsequences with the minimum distance.

Continuous queries and data stream management Broadly related work includes DSMSs. Their common goal is to provide a general-purpose infrastructure for the efficient management of data streams. Sample systems include Aurora [1], Stream [44], Telegraph [12], Gigascope [19], and OSCAR [13]. Algorithmic work includes query processing [41], scheduling [6, 11], and load shedding [20, 64]. As regards continuous queries, Arasu et al. [3] studied the memory requirements of continuous queries over relational data streams. SOLE [43] is a scalable algorithm for continuous spatio-temporal queries in data streams. To address multiple streams and queries, it provides a framework with caching of uncertainty regions and a shared operator on a shared buffer.

Approximation and adaptivity are also key features for DSMSs, such as sampling [7], sketches [17, 23, 27], statistics [21, 28], and wavelets [30]. The main goal of these methods is to estimate a global aggregate (e.g., sum, count, average) over a fixed window on the recent data.

The emphasis in the above works is to support traditional SQL queries on streams. None of them try to find patterns.

Stream mining. Many other previous studies have attempted pattern discovery in a streaming scenario. Mueen et al. [46] presented the first online motif discovery algorithm to accurately monitor and maintain motifs, which represent repeated subsequences in time-series, in real time. AWSOM [50] is one of the first streaming algorithms for forecasting, and it is used to discover arbitrary periodicities in a time sequence. Zhu et al. [73] focused on monitoring multiple streams in real time and proposed StatStream, which computes pairwise correlations among all streams. The SPIRIT method [51] is used to address the problem of capturing correlations and finding hidden variables corresponding to trends in collections of coevolving data streams. BRAID [60] detects lag correlations between data streams by using geometric probing and smoothing to approximate the exact correlation. Papadimitriou et al. [52] proposed an algorithm for discovering optimal local patterns, which concisely describe the main trends in data streams. DynaMMo [40] summarizes and compresses multiple sequences and finds latent variables among them.

On the other hand, there are effective methods that address massive time-series streams as applications for data center management. Reeves et al. [56] addressed the problem of the space-efficient archiving of time-series streams and the fast processing of several statistical and data mining queries regarding that archived data. They focused on the problem that traditional database systems have addressed space-efficient archiving and query processing separately, and proposed Cypress, which preprocesses and decomposes each data stream into a small number of substreams, and answers common queries directly from a set of them rather than reconstructing the original stream. Mueen et al. [47] considered the problem of computing all-pair correlations in a warehouse containing a large number of time-series. A high I/O and CPU overhead make the fast computation of correlations a challenging issue. They proposed a caching algorithm to optimize overall I/O cost and two approximation algorithms to reduce CPU costs.

These techniques focus on trend detection, correlation, motif discovery, and prediction and so are not solutions for our goal, which is to find common local patterns based on DTW.

In our experiment on CrossMatch, we used scatter plots to show its outputs, which were the optimal subsequence pairs. Recurrence plot [24] and dot plot [69] have been proposed for visual sequence analysis and mining of time-series data; they focus on the visualization of the similar parts of sequences on a scatter plot. Our objective is to identify which of the subsequences of \(X\) and \(Y\) are similar by applying the DTW approach in an online manner, and so differs from their objective and approach.

3 Problem definition

In this section, we introduce DTW [9, 54] and then define the problem that forms our objective. The main symbols used in this paper are shown in Table 1.

Table 1 Definitions of main symbols
Full size table

3.1 Preliminaries

Dynamic time warping is a transformation that allows sequences to be stretched along the time axis to minimize the distance between them (see Fig. 2). The DTW distance of two sequences is the sum of the tick-to-tick distances after the two sequences have been optimally warped to match each other. To align two sequences, we construct a ‘time warping matrix’. The warping path is a set of grid cells in the time warping matrix, which represents the alignment between the sequences. Consider two sequences, \(X=(x_1, x_2,\ldots , x_n)\) of length \(n\) and \(Y=(y_1, y_2,\ldots , y_m)\) of length \(m\). Their DTW distance \(D(X,Y)\) is defined as

$$\begin{aligned}&D(X,Y) = d(n, m)\nonumber \\&d(i, j) = ||x_i - y_j||+ \min \left\{ \begin{array}{l} d(i, j-1) \\ d(i-1, j) \\ d(i-1, j-1) \end{array}\right.\\&d(0,0) = 0, \quad d(i,0) = d(0,j)= \infty \nonumber \\&(i = 1,\ldots , n; j = 1,\ldots , m).\nonumber \end{aligned}$$
(1)

Note that \(||x_i - y_j|| = (x_i - y_j)^2\) is the distance between two numerical values in cell \((i, j)\) of the time warping matrix. Note that other choices (say, absolute difference \(||x_i - y_j|| = |x_i - y_j|\)) can also be used; our algorithm is completely independent of the choice made. To avoid degenerated matching, where a relatively small section of one sequence maps onto a relatively large section of another, the warping path is limited by global constraints. The warping scope \(w\) is the area that the warping path is allowed to visit in the time warping matrix. The Sakoe–Chiba band [57] is a well-known global constraint that restricts the warping path to the range of \(|i - j |\le w\).

Fig. 2
figure 2

Illustration of DTW. The left figure indicates the alignment of measurements. The right figure indicates the optimal warping path in a warping scope

Full size image

DTW requires \(O(nm)\) time since the time warping matrix consists of \(nm\) cells. Note that the space complexity is \(O(m)\) (or \(O(n)\)) since the algorithm needs only two columns (i.e., the current and previous columns) of the time warping matrix to compute the DTW distance. By using the warping scope, the time complexity is reduced to \(O(nw+mw)\). The space complexity is \(O(w)\) because we need only \(2w\) cells.

3.2 Cross-similarity

Data stream \(X\) is a discrete, semi-infinite sequence of numbers \(x_1\), \(x_2\), \(\ldots \), \(x_n\), \(\ldots \), where \(x_n\) is the most recent value. Note that \(n\) increases with every new time-tick. Let \(X[i_s:i_e]\) be the subsequence of \(X\) that starts from time-tick \(i_s\) and ends at \(i_e\), and let \(Y[j_s:j_e]\) be the subsequence of \(Y\) that starts from time-tick \(j_s\) and ends at \(j_e\). The lengths of \(X[i_s:i_e]\) and \(Y[j_s:j_e]\) are \(l_x=i_e-i_s+1\) and \(l_y=j_e-j_s+1\), respectively. Our goal is to find the common local patterns of sequences by data stream processing based on DTW. That is, we want to detect subsequence pairs that satisfy

$$\begin{aligned} D(X[i_s:i_e], Y[j_s:j_e]) \le \varepsilon L(l_x, l_y), \end{aligned}$$
(2)

where \(D(X[i_s:i_e], Y[j_s:j_e])\) is the DTW distance between \(X[i_s:i_e]\) and \(Y[j_s:j_e]\), \(\varepsilon \) is a distance threshold, and \(L\) is a function that sets the length of the subsequence. In this paper, the algorithm uses \(L(l_x, l_y) = (l_x+l_y)/2\), which is the average length of the two subsequences, but the user can employ any other choice (e.g., \(L(l_x, l_y) = \text{ max}(l_x, l_y)\) or \(L(l_x, l_y)=\text{ min}(l_x, l_y)\)). The DTW distance increases as the subsequence length increases since it is the sum of the distances between elements. Therefore, the distance threshold should be proportional to the subsequence length. Accordingly, we set it at \(\varepsilon L(l_x, l_y)\).

Equation (2) allows us to detect subsequence pairs without regard to the subsequence length. In practice, however, we might detect shorter and meaningless matching pairs due to the influence of noise. We introduce the concept of subsequence match length to enable us to discard such meaningless pairs and to detect the optimal pairs that satisfy ‘real’ user requirements. We formally define the ‘cross-similarity’ between \(X\) and \(Y\), which indicates common local patterns.

Definition 1

(Cross-similarity [65]) Given two sequences \(X\) and \(Y\), a distance threshold \(\varepsilon \), and a threshold of subsequence length \(l_{\min }\), \(X[i_s:i_e]\) and \(Y[j_s:j_e]\) have the property of cross-similarity if this sequence pair satisfies the following condition.

$$\begin{aligned} D(X[i_s:i_e], Y[j_s:j_e]) \le \varepsilon (L(l_x, l_y)-l_{\min }). \end{aligned}$$
(3)

The minimum length \(l_{\min }\) of subsequence matches should be given by the users. The subsequences that satisfy this equation are guaranteed to have lengths exceeding \(l_{\min }\). We also agree that the user should select the length function \(L\) as well as \(l_{\min }\) to obtain desirable results.

We should also mention the following point: Whenever a subsequence pair matches, there will be several other matches that strongly overlap the ‘local minimum’ best match. Specifically, an overlap is simply the relation that two subsequence pairs have a common alignment, which is defined as follows:

Definition 2

(Overlap) Given two warping paths for subsequence pairs of \(X\) and \(Y\), their overlap is defined as the condition where the paths share at least one element.

Overlaps provide the user with redundant information and would slow down the algorithm since all useless ‘solutions’ are tracked and reported. Our solution is to detect the local best subsequences from the set of overlapping subsequences. Thus, our goal is to find the best match of cross-similarity.

Problem 1

Given two sequences \(X\) and \(Y\), thresholds \(\varepsilon \), and \(l_{\min }\) report all subsequence pairs, \(X[i_s:i_e]\) and \(Y[j_s:j_e]\), that satisfy the following conditions.

  1. 1.

    \(X[i_s:i_e]\) and \(Y[j_s:j_e]\) have the property of cross-similarity.

  2. 2.

    \(D(X[i_s:i_e], Y[j_s:j_e])-\varepsilon (L(l_x, l_y)-l_{\min })\) is the minimum value among the set of overlapping subsequence pairs that satisfies the first condition.

Hereafter, we use ‘qualifying’ subsequence pairs to refer to pairs that satisfy the first condition, and we use ‘optimal’ subsequence pairs to refer to pairs that satisfy both conditions.

Typically, new elements in data streams, that is, those that have occurred recently, are usually more significant than those in the distant past [18]. To limit the cell in the matrix and focus on recent elements, we utilize a concept of global constraint for DTW, namely the Sacoe–Chiba band [57]. More specifically, for each sequence \(X\) and \(Y\), we compute the cells from the recent element (e.g., \(x_n\) or \(y_m\)) to an element of the warping scope \(w\) ago. If \(m = n\), the warping scope is exactly equal to the Sakoe–Chiba band.

4 Proposed method

In this section, we describe a straightforward solution to find the best match of cross-similarity in data streams and also present our one-pass algorithm, CrossMatch.

4.1 Naive solution

The most straightforward solution to this problem is to consider all possible subsequences of \(X[i_s:i_e] \ (1 \le i_s < i_e \le n)\) and all possible subsequences of \( Y[j_s:j_e] \ (1 \!\le \! j_s \!<\! j_e \!\le \! m)\) in the warping scope and apply the standard DTW dynamic programming algorithm. We call this method Naive.

Let \(d_{i, j}(p, q)\) be the distance of cell \((p, q)\) in the time warping matrix that starts from \(i\) on the \(x\)-axis and \(j\) on the \(y\)-axis, and let \(w\) be the width of the warping scope. The distance of the subsequence matching between \(X\) and \(Y\) can be obtained as follows.

$$\begin{aligned} \begin{aligned}&D(X[i_s:i_e],Y[j_s:j_e])= d_{i_s, j_s}(l_x, l_y)\\&d_{i, j}(p, q) \!=\! ||x_{i+p-1} \!-\! y_{j+q-1}|| \!+\! \min \! \left\{ \begin{array}{l} d_{i,j}(p, q\!-\!1) \\ d_{i,j}(p\!-\!1, q)\\ d_{i,j}(p\!-\!1, q\!-\!1) \end{array}\right.\\&d_{i,j}(0,0) = 0, \quad d_{i,j}(p,0) = d_{i,j}(0,q) = \infty \\&(i = 1,\ldots , n; \ p = 1,\ldots , n\!-\!i\!+\!1;\\&j = 1,\ldots , m; \ q = 1,\ldots , m\!-\!j\!+\!1;\\&n-w \le i+p \le n; \ m-w \le j+q \le m;) \end{aligned} \end{aligned}$$
(4)

The naive solution creates a new matrix at every new time-tick and updates the distance arrays of incoming \(x_i\) at time-tick \(i\) and that of incoming \(y_j\) at time-tick \(j\) in each existing time warping matrix. It then determines the subsequence pair for which \(D(X[i_s\!:\!i_e], Y[j_s\!:\!j_e])\!-\!\varepsilon (L(l_x, l_y)\!-\!l_{\min })\) is the minimum value among the set of overlapping subsequence pairs.

Figure 3 shows an example of a naive solution to the problem of subsequence matching. Let \(w\) be the width of the warping scope (the gray cell in the figure). The naive solution updates \(O(w)\) distance values per time-tick on each matrix when an element of the sequence arrives. The naive solution requires \(O(nw^2 \!+\! mw^2)\) time (per update) and space because it has to handle a total of \(O(nw + mw)\) matrices to compute the DTW distance. In practice, it is not feasible to compute the distance in a streaming setting.

Fig. 3
figure 3

Illustration of subsequence matching using the naive solution. The naive solution maintains matrices starting from every time-tick

Full size image

4.2 CrossMatch

As mentioned in the previous section, the naive solution creates too many matrices because it computes the distance values between all possible subsequences. The distance threshold is proportional to the subsequence length (cf. Definition 1). The naive solution attempts to find the subsequence pairs semipermanently in each matrix. If we prune dissimilar subsequence pairs and reduce the number of matrices, the distance computations become much more efficient. Our method is motivated by this idea.

Our method, CrossMatch, computes the similarity score that corresponds to the DTW distance and identifies dissimilar subsequences. We find ‘good’ matches in a single matrix efficiently by pruning the subsequences (see Fig. 4). Our method, which realizes these concepts, consists of three ideas: a new scoring function, a position matrix, and a streaming algorithm that uses them.

Fig. 4
figure 4

Illustration of CrossMatch. The black cells indicate the warping paths of the optimal subsequence pairs and the gray cells indicate the warping scope

Full size image

4.2.1 Scoring function

To identify the dissimilar subsequences early, we propose computing the DTW distance indirectly by using a scoring function. The scoring function has the following two characteristics: (a) it provides a non-negative cumulative score, and (b) its operation is reversible with respect to the DTW distance.

The scoring function is essentially based on the dynamic programming approach. Whereas the DTW computes the minimum cumulative distance, our function computes the maximum cumulative score corresponding to the DTW distance with a score matrix. The score is determined by accumulating the difference between the threshold and the distance between the elements in the score matrix. Thus, we can recognize a dissimilar subsequence pair since the score has a negative value if the subsequence pair does not satisfy the first condition of Problem 1.

The scoring function selects the cell with the maximum cumulative score from the neighboring cells, and if the score is negative, the function initializes the score to zero and then restarts the computation from the cell. This operation allows us to discard unqualifying, non-optimal subsequence pairs.

Definition 3

(Score matrix [65]) Given two sequences, \(X = (x_1, \ldots , x_i, \ldots , x_n)\) and \(Y = (y_1, \ldots , y_j, \ldots , y_m)\), and the width of the warping scope \(w\), score \(V(X[i_s:i_e], Y[j_s:j_e])\) of \(X[i_s:i_e]\) and \(Y[j_s:j_e]\) is defined as:

$$\begin{aligned} \begin{aligned}&V(X[i_s:i_e], Y[j_s:j_e]) = v(i_e, j_e) \\&v(i, j)= \max \left\{ \begin{array}{l} 0\\ \varepsilon b_v - ||x_i - y_j|| + v(i, j-1)\\ \varepsilon b_h - ||x_i - y_j|| + v(i-1, j)\\ \varepsilon b_d - ||x_i - y_j|| + v(i-1, j-1) \end{array}\right.\\&v(0,0) = v(i,0) = v(0,j)=0\\&(i = 1,\ldots , n;\ j = 1,\ldots , m;\\&\ n-w \le i \le n;\ m-w \le j \le m;). \end{aligned} \end{aligned}$$
(5)

The scoring function operation is reversible with respect to the DTW distance. That is, the score of the qualifying subsequence pair with a positive value is easily transformed into the DTW distance. Symbols \(b_v\), \(b_h\), and \(b_d\) in Eq. (5) indicate a weight function for each direction, which makes transformation between the score and the DTW distance possible. These values are determined as a function of the subsequence length. For example, for \(L(l_x, l_y) = (l_x+l_y)/2\), the current \(L\) value increases by \(1/2\) if the score of a vertical or horizontal cell is chosen, and it increases by \(1\) if the score of a diagonal cell is chosen. Thus, we obtain \(b_v = b_h = 1/2\) and \(b_d =1\), respectively, for these directions.Footnote 1 The scoring function is designed so that the sum of the weights on the warping path (i.e., \(b_v, \ b_h, \ \text{ and} \, b_d\)) is equal to subsequence length \(L\). Therefore, it guarantees reversibility between the DTW distance and the score and finds the qualifying subsequence pairs without any omissions. The DTW distance of a subsequence pair is computed from the score and the subsequence length as follows:

$$\begin{aligned} D(\!X[i_s\!:\!i_e],\!Y[j_s\!:\!j_e])&= \varepsilon L(l_x,\!l_y\!)\!-\!V(\!X[i_s\!:\!i_e], \!Y[j_s\!:\!j_e]) \nonumber \\&s.t.\,V(X[i_s\!:\!i_e]),\!Y[j_s\!:\!j_e]) \!>\! 0.\qquad \end{aligned}$$
(6)

Equation (6) holds for the time warping and the score matrices, which have the same starting position \((i_s, j_s)\). The details are provided in Sect. 4.3.

Example 1

Assume that we have two sequences of \(X=(5, 12, 6, 10, 3, 18)\), \(Y=(11, 9, 4, 2, 9, 13)\), and \(\varepsilon = 14\), \(l_{\min } = 2\), and \(w = 3\). Figure 5a shows the score matrix. The dark cell, which has the highest score, shows the optimal subsequence pair and indicates that the score is \(\varepsilon b_d \!-\! ||x_5\!-\!y_4|| \!+\! v(4,3)=49\) and the end position is \((i_e, j_e)\!=\!(5, 4)\). The light cells show qualifying subsequence pairs. The cells that contain zero identify dissimilar subsequence pairs.

Fig. 5
figure 5

Example of cross-similarity detection. The light cells signify cross-similarity, and the dark cell in each matrix shows the best match

Full size image

4.2.2 Position matrix

The scoring function tells us (a) where the subsequence match ends and (b) what the resulting score is. However, we lose the information about the starting position of the subsequence. This is the motivation behind our second idea, a position matrix: We store the starting position to keep track of the qualifying subsequence pair in a streaming fashion.

Definition 4

(Position matrix [65]) The position matrix stores the starting position of each subsequence pair. The starting position \(s(i, j)\) corresponding to score \(v(i, j)\) is computed as follows:

$$\begin{aligned} s(i, j) \!=\! \left\{ \begin{array}{l} \!s(i, j\!-\!1)\quad {(v(i, j\!-\!1) \ne 0 \ \wedge \ v(i, j)}\\ \qquad \qquad \qquad \qquad {=\, \varepsilon b_v \!-\! ||x_i-y_j|| + v(i, j-1))}\\ \!s(i\!-\!1, j)\quad {(v(i\!-\!1, j) \ne 0 \ \wedge \ v(i, j)}\\ \qquad \qquad \qquad \qquad {=\, \varepsilon b_h \!-\! ||x_i-y_j|| + v(i-1, j))}\\ \!s(i\!-\!1, j\!-\!1) {(v(i\!-\!1, j\!-\!1) \ne 0 \ \wedge \ v(i, j)}\\ \qquad \qquad \qquad \qquad {=\, \varepsilon b_d \!-\! ||x_i\!-\!y_j||\!+\! v(i\!-\!1, j\!-\!1))}\\ \!(i, j) \qquad \quad {(otherwise)}. \end{array}\right. \end{aligned}$$
(7)

The starting position is described as a coordinate value; \(s(i_e, j_e)\) indicates the starting position \((i_s, j_s)\) of the subsequence pair \(X[i_s:i_e]\) and \(Y[j_s:j_e]\). We update the starting position in the position matrix as well as the score in the score matrix. We can identify the optimal subsequence that gives the maximum score during stream processing since exactly the same warping path is maintained in the score and position matrices. Moreover, the starting position of the shared cell is maintained through the subsequent alignments because we repeat the operation, which maintains the starting position of the selected previous cell. Thus, we know the overlapping subsequence pairs from the fact that the starting positions match.

Example 2

Figure 5b shows the position matrix corresponding to the score matrix in Fig. 5a. In cell \((5,4)\), the starting position \((2,1)\) is maintained because the scoring function selects the score of cell \((4,3)\) in the score matrix. By combining both matrices, we can identify the position of the optimal subsequence pair \(X[2:5]\) and \(Y[1:4]\). On the other hand, there are many overlapping subsequence pairs that have the same starting position \((2,1)\). Of these, we select the subsequence pair with the highest score as the optimal pair because we can determine the overlapping subsequence pairs from the position matrix.

Next, we show how subsequence pairs are pruned. The pruned subsequence pairs fall into one of the following two categories: (1) subsequence pairs that are absolutely not reflected in two matrices (i.e., the score and the position matrices) and (2) subsequence pairs that are pruned during the computation process. In any case, our method is designed so that we can evaluate the cross-similarity between sequences from the score value, and guarantees that the pruned subsequence pairs are not optimal by using the fact that the overlapping subsequence pairs in cell \((i,j)\) have the same warping paths in the subsequent alignments (we will provide detailed proofs in Sect. 4.3).

Example 3

An example of case (1) corresponds to the subsequence pairs starting at \((3,2)\) in Fig. 5. In cell \((3,2)\), our method has to select one pair from neighboring cells since all neighboring cells include positive scores, and it prunes the subsequence pairs that have the starting position \((3,2)\). An example of case (2) corresponds to the subsequence pairs starting at \((1,3)\). In cell \((4,5)\), our method chooses the subsequence pair starting at \((2,1)\) because the pair has the maximum value. That is, the subsequence pair that has the starting position \((1,3)\) is pruned although the score indicates a positive value.

4.2.3 Streaming algorithm

We now have all the pieces needed to answer the question: how do we find the optimal subsequence pairs? Every time \(x_n\) is received at time-tick \(n\), our algorithm, CrossMatch, incrementally updates the score \(C^{\prime }_v \!=\! v(n,j)\) and starting position \(C^{\prime }_s \!=\! s(n,j)\) and retains the end position \(C^{\prime }_e \!=\! (n,j)\). We use candidate array \(\mathcal S\) to find the optimal subsequence pair and store the best pair \(C\) (i.e., score \(C_v\), starting position \(C_s\), and end position \(C_e\)) in a set of overlapping subsequence pairs. CrossMatch reports the optimal subsequence pair after confirming that it cannot be replaced by the upcoming subsequence pairs (i.e., there are no overlapping subsequence pairs). The upcoming candidate subsequence pairs do not overlap the captured optimal subsequence pair if the starting positions in the position matrix satisfy the following condition.

$$\begin{aligned} (\forall _i, s(i, m) \ne C_s) \ \wedge \ (\forall _j, s(n, j) \ne C_s). \end{aligned}$$

CrossMatch reports the similarity of the subsequence pair as the DTW distance. The DTW distance is obtained from the score and the subsequence length, as shown in Eq. (6).

The above procedure provides the foundation of our efficient detection of similar pairs. Algorithm 1 shows the details. We keep only two columns (i.e., the current and previous columns) for each \(X\) and \(Y\) in the two matrices. In this algorithm, we focus on computing the scores and the starting positions when we receive \(x_n\) at time-tick \(n\). Note that the scores and the starting positions of incoming \(y_m\) at time-tick \(m\) are also computed similarly by this algorithm.

figure a1

CrossMatch requires three parameters, \(l_\mathrm{min}\), \(w\), and \(\varepsilon \). The subsequence length \(l_\mathrm{min}\) and the parameter \(\varepsilon \) are set based on the pattern the user wants to search. It is desirable to set the values according to the applications. The warping scope \(w\) determines the computation range in each matrix. At the same time, it asks the user how far back into the past the algorithm needs to go. If the user wants to search for subsequence pairs during the present time-tick and a time-tick in the relatively distant past, it is better to set a large \(w\). In our experiments, we simply use reasonable values for every data set, and we show that this way of setting parameters is sufficient for CrossMatch to verify the detection of the optimal subsequence pairs.

Example 4

Again, assume two sequences of \(X=(5, 12, 6, 10, 3, 18)\), \(Y=(11, 9, 4, 2, 9, 13)\), and \(\varepsilon = 14\), \(l_\mathrm{min} = 2\), and \(w = 3\) in Fig. 5. To simplify the example of our algorithm with no loss of generality, we assume that \(x_i\) and \(y_j\) arrive in alternately. At each time-tick, the algorithm updates the scores and the starting positions. At \(i=4\), we update the cells from \((4, 1)\) to \((4, 3)\) and identify a candidate subsequence, \(X[2:4]\) and \(Y[1:3]\), starting at \((2, 1)\), whose score \(v(4,3)=36\) is greater than \(\varepsilon l_\mathrm{min}\). At \(j=4\), we update the cells from \((1, 4)\) to \((4, 4)\). Although no subsequences satisfying the condition are detected, we do not report the subsequence of \(X[2:4]\) and \(Y[1:3]\) since it is possible that this pair could be replaced by upcoming subsequences. We then capture the optimal subsequence pair of \(X[2:5]\) and \(Y[1:4]\) at \(i=5\). We finally report the subsequence as the optimal subsequence at \(j=6\) since we can confirm that none of the upcoming subsequences can be optimal. Figure 6 shows time warping matrix starting at \((2,1)\) in the naive solution, which includes the optimal subsequence pair in Fig. 5. In the score and the position matrices, the subsequence pairs that have the starting position \((2,1)\) correspond to the pairs on the time warping matrix in Fig. 6. From Eq. (6), we have \(\varepsilon L(4,4)\!-\!V(X[2\!:\!5],Y[1\!:\!4]) = 14 \cdot 4 \!-\! 49 = 7 = D(X[2\!:\!5],Y[1\!:\!4])\).

Fig. 6
figure 6

Time warping matrix starting at (2,1) in the naive solution

Full size image

In this paper, we focus on finding only the optimal subsequence pairs. We provide one alternative with regard to the output of similar subsequence pairs. In a stream setting, it is desirable to report similar subsequence pairs as soon as possible. To report the similar subsequence pairs without delay, we firstly report the foremost subsequence pair, that is, the first pair satisfying the threshold among the set of overlapping pairs, and thereafter update the pair with the optimal subsequence pair. For example, Fig. 7 shows the foremost subsequence pairs for the Humidity data set in Fig. 1. We show the detailed comparison of their positions in Table 2. Note that \((i_s, j_s)\) is the starting position and \((i_e, j_e)\) is the end position. Unlike Fig. 1, it is obvious to shorten the reporting time. Thus, we can provide a solution that is more suitable for a streaming scenario.

Fig. 7
figure 7

Discovery of foremost subsequence pairs using Humidity. The subsequence pairs in the middle of alignments are detected, unlike the optimal subsequence pairs in Fig. 1

Full size image
Table 2 Comparison with positions of optimal and foremost subsequence pairs
Full size table

4.3 Theoretical analysis

We introduce a brief theoretical analysis that confirms the accuracy and complexity of CrossMatch.

4.3.1 Accuracy

Lemma 1

Given two sequences \(X\) and \(Y\), Problem 1 is equivalent to the following conditions.

  1. 1.

    \(V(X[i_s\!:\!i_e],Y[j_s\!:\!j_e]) \ge \varepsilon l_\mathrm{min}\)

  2. 2.

    \(V(X[i_s\!:\!i_e],Y[j_s\!:\!j_e])- \varepsilon l_\mathrm{min}\) is the maximum value in each group of subsequence pairs that the warping path crosses.

Proof

See Appendix 1. \(\square \)

Lemma 2

CrossMatch guarantees the output of the optimal subsequence pairs.

Proof

See Appendix 2. \(\square \)

4.3.2 Complexity

Let \(X\) and \(Y\) be evolving sequences of lengths \(n\) and \(m\), respectively.

Lemma 3

The naive solution requires \(O(nw^2 + mw^2)\) time (per update) and space to discover cross-similarity.

Proof

See Appendix 3. \(\square \)

Lemma 4

CrossMatch requires \(O(w)\) (i.e., constant) time (per update) and space to discover cross-similarity.

Proof

See Appendix 4. \(\square \)

5 Sampling approach

As mentioned above, CrossMatch detects cross-similarity in constant time and space. The next question is what we can do in the highly likely case that the users need more efficient solutions given that, in practice, they require high accuracy, not a theoretical guarantee. This is our motivation for introducing an approximation for CrossMatch.

What approximate techniques are suitable for CrossMatch? An efficient idea involves the data reduction in a sequence. Optimal alignments of DTW correspond to matching the elements in time. To find optimal subsequence pairs by approximation, we choose to keep the sequence, which is transformed by data reduction operated in the time domain. As an extended version of CrossMatch, we propose compressing the matrices using a sampling approach. As we show later, this decision significantly improves both space cost and response time, with negligible effect on the mining results.

As the first step, we consider the following theorem.

Theorem 1

(Sampling theorem) If a continuous function contains no frequencies higher than \(f_{high}\), it is completely determined by its value at a series of points less than \(1/2f_{high}\) apart.

Poorf

See [39]. \(\square \)

In the theorem, the minimum sampling frequency, \(f_{Nq} = 2f_{high}\), is called the Nyquist frequency. We utilize this theorem for sampling the sequences. That is, we use coarse sequences yielded by sampling based on the theorem and detect the cross-similarity. Since the original sequence is sampled once for each \(f_{Nq}\) value, that is, \(T=1/f_{Nq}\), we greatly reduce in the size of the matrix.

5.1 Scoring function

How do we compute the score between sampled sequences? Intuitively, the key idea is that when we select one of the neighboring cells for score computation, we interpolate the distance values that were dropped by sampling. In the score computation between sampled sequences, there are \(T\!-\!1\) hidden cells that represent the missing values between the current cell (i.e., the cell that we should compute now) and its neighboring cells. We approximate the distance values, which should be provided by the hidden cells, by using the distance value in the current cell. Since the sampled sequences are obtained based on the sampling theorem, this is a suitable approximation.

Let \(X\) and \(Y\) be two sequences of lengths \(n\) and \(m\) with sampling periods \(T_x\) and \(T_y\), respectively. Also, let \(\mathcal{X }\) = \((\mathrm{x}_{1},\ldots , \mathrm{x}_{i},\ldots , \mathrm{x}_{\lfloor n/T_x \rfloor })\) and \(\mathcal{Y}\) = \((\mathrm{y}_{1},\ldots , \mathrm{y}_{j},\ldots , \mathrm{y}_{\lfloor m/T_y \rfloor })\) be sampled sequences of \(X\) and \(Y\), respectively. We obtain the scores of the subsequences of \(\mathcal{X}\) and \(\mathcal{Y}\) as follows.

$$\begin{aligned}&V(\mathcal{X}[i_s:i_e], \mathcal{Y}[j_s:j_e]) = v(i_e, j_e)\nonumber \\&v(i, j) \!= \!\text{ max} \left\{ \begin{array}{l} 0\\ \varepsilon b_v \!- \!T_y\! \cdot \!||\mathrm{x}_{i} \!-\! \mathrm{y}_{j}|| \!+\! v(i, j\!-\!1)\\ \varepsilon b_h \!-\! T_x\! \cdot \!||\mathrm{x}_{i} \!-\! \mathrm{y}_{j}|| \!+ \!v(i\!-\!1, j)\\ \varepsilon b_d \!-\! \text{ max}(T_x, T_y)\! \cdot \!||{\!\mathrm x}_{i} \!-\! {\!\mathrm y}_{\!j}||\! +\! v(\!i\!-\!1, \!j\!-\!1) \end{array}\right.\nonumber \\&v(0,0)\! =\! v(i,0) \!=\! v(0,j)\!=\!0\nonumber \\&(i\! = \!1,\ldots , \lfloor n/T_x \rfloor ;\ j \!=\! 1,\ldots ,\lfloor m/T_y \rfloor ;\nonumber \\&\lfloor (n \!-\! w)/T_x \rfloor \!\le \! i \!\le \! \lfloor n/Tx \!\rfloor ; \ \lfloor \!(m \!-\! w)/T_y \!\rfloor \! \!\le \! j \!\le \! \lfloor \! m/Ty\!\rfloor ;)\nonumber \\ \end{aligned}$$
(8)

We interpolate \(T_y\) values if we select the score of the vertical cell. Similarly, we interpolate \(T_x\) values in the horizontal direction and max(\(T_x\), \(T_y\)) values in the diagonal direction. Furthermore, we modify the weight function for the sampling approach. For \(L(l_x, l_y) \!=\! (l_x\!+\!l_y)/2\), the current \(L\) value increases by \(T_y/2\) if the score of a vertical cell is chosen, by \(T_x/2\) if the score of a horizontal cell is chosen, and by \((T_x+T_y)/2\) if the score of a diagonal cell is chosen. Thus, we obtain \(b_v \!=\! T_y/2\), \(b_h\! = \!T_x/2\), and \(b_d \!= \!(T_x+T_y)/2\) for these directions.

5.2 Position matrix

The position matrix for the sampling approach is similar to Eq. (7). We keep the starting position of the previous cell if any of the three neighboring cells is selected. In other cases, we appropriately set the starting position in concert with the sampling periods \(T_x\) and \(T_y\). More specifically, the starting position \(s(i,j)\) is computed as follows.

$$\begin{aligned}&s(i, j) =\nonumber \\&\left\{ \begin{array}{ll} (i \cdot T_x, j \cdot T_y)\qquad \qquad \quad {(v(i,j) \le 0)} \\ s(i, j\!-\!1) \qquad \qquad {(v(i, j\!-\!1) \ne 0 \ \wedge \ v(i, j)}\\ \qquad \qquad \qquad \qquad \qquad \quad {= \varepsilon b_v - T_y\! \cdot \!||\mathrm{x}_{i} \!-\! \mathrm{y}_{j}|| + v(i, j\!-\!1)}\\ s(i\!-\!1, j) \qquad \qquad {(v(i\!-\!1, j) \ne 0 \ \wedge \ v(i, j)}\\ \qquad \qquad \qquad \qquad \qquad \quad {= \varepsilon b_h - T_x\! \cdot \!||\mathrm{x}_{i} \!-\! \mathrm{y}_{j}|| + v(i\!-\!1, j)}\\ s(i\!-\!1, j\!-\!1) \qquad {(v(i\!-\!1, j\!-\!1) \ne 0 \, \wedge \, v(i, j) = \varepsilon b_d}\\ \qquad \qquad \qquad \qquad \qquad \quad {- \text{ max}(T_x, T_y)\! \cdot \!||\mathrm{x}_{i} \!-\! \mathrm{y}_{j}|| + v(i\!-\!1, j\!-\!1)}\\ ((i\!-\!1) \cdot T_x \!+\! 1, (j\!-\!1) \cdot T_y \!+\! 1) \qquad \quad {(otherwise)}. \end{array}\right.\nonumber \\ \end{aligned}$$
(9)

5.3 Streaming algorithm

Algorithm 2 shows a detailed description of our sampling approach. The algorithm reflects the information about the skipped elements in the next computation and approximately computes the score and the position of the subsequence pair. The basic procedure is the same as that of the original version of CrossMatch (i.e., Algorithm 1); however, we can greatly reduce the space requirement and the computation cost by the sampling, which faithfully reconstructs the original sequence.

Lemma 5

Let \(T\) be the sampling period. With the sampling approach, CrossMatch requires \(O(w/T)\) time (per update) and space.

Proof

See Appendix 5. \(\square \)

5.4 Adaptive sampling approach

We discussed how to compute the score assuming that the fixed sampling period of each sequence is given. Next, we focus our attention on handling the variation in the sampling period. Assuming that we cannot know the elements of a data stream in advance, the power rate between high and low frequencies might vary over time. This means that the frequency range varies locally in the time domain. We want to incorporate this frequency range variation into CrossMatch. Thus, CrossMatch updates the sampling period in stream processing. We call this method the adaptive sampling approach as opposed to the sampling approach.

figure a2

Let \(\mathcal{X } \!=\! (\mathrm{x}_{1},\ldots , \mathrm{x}_{i},\ldots , \mathrm{x}_{n^{\prime }})\), be the sampled sequences of \(X\), and \(\mathcal{T }_{x} \!=\! (t_{\mathrm{x}_{1}},\ldots , t_{\mathrm{x}_{i}}, \ldots , t_{\mathrm{x}_{n^{\prime }}})\) be the sampling period of \(\mathcal{X }\) in each time-tick. In the adaptive sampling approach, the number of hidden cells varies according to the sampling period in each time-tick. We compute the appropriate sampling period in each cell and approximate the distance values of the hidden cells accordingly. On the other hand, we determine the weights of each direction dynamically since the current \(L\) value is determined by the sampling period in each time-tick. For \(L\!=\!(l_x\!+\!l_y)/2\), the weight of the horizontal direction in cell \((i,j)\) is \(b_h=t_{\mathrm{x}_{i}}/2\) and the others are similarly set by the sampling periods. In the adaptive sampling approach, we constantly use the sampling period, which reflects the sequence of recent time-ticks. Thus, this approach would be more powerful when the sequence consists of high and low frequencies.

Incremental algorithms have been proposed for computing the frequency in the stream sense (e.g., [29, 49]). CrossMatch can utilize any and all of these solutions to compute the frequency efficiently. However, this research topic is beyond the scope of this paper.

Two sampling approaches do not guarantee their error-bound theoretically because the alignment of DTW depends on the data sequence and changes if the data sequence is sampled with a different sampling period. However, we show that their errors are very small in Sect. 7.3.

6 Discovery of group-similarity

So far, we have assumed the problem of cross-similarity between two data streams. For more generality, we would like to make CrossMatch more flexible. We now tackle a more challenging problem: How do we efficiently identify common local patterns among multiple data streams? A useful feature of CrossMatch is that it can be effectively extended to this case.

Given multiple data streams (more than two sequences), we want to find ‘group-similarity,’ which means the cross-similarity among them. The work in [62] has addressed the problem of similarity group-by that supports grouping based on tuples in a database. On the other hand, group-similarity provides grouping based on similar patterns. For example, in sensor networks, measurement values arriving from many different sensors have to be examined dynamically. CrossMatch makes it possible to reduce a large number of streams to just a handful of common patterns that compactly describe the key features. More importantly, the time and space requirements are constant per update.

We formally define group-similarity below. To simplify our presentation, we focus on three sequences \(X\), \(Y\), and \(Z\). We first present the DTW distance for the three sequences.

Consider three sequences, \(X = (x_1, x_2,\ldots , x_{n_1})\), \(Y = (y_1, y_2,\ldots , y_{n_2})\), and \(Z = (z_1, z_2,\ldots , z_{n_3})\). Their DTW distance \(D(X, Y, Z)\) is defined asFootnote 2

$$\begin{aligned} D(X,Y,Z)&= d(n_1, n_2, n_3)\nonumber \\ d(i, j, k)&= ||x_i - y_j|| + ||y_j - z_k|| + ||z_k - x_i||\nonumber \\&\qquad + \min \left\{ \begin{array}{l} d(i, j-1, k) \\ d(i-1, j, k) \\ d(i-1, j-1, k)\\ d(i, j, k-1)\\ d(i-1, j, k-1)\\ d(i, j-1, k-1)\\ d(i-1, j-1, k-1). \end{array}\right.\nonumber \\ \end{aligned}$$
(10)

The time warping matrix for the three sequences consists of \(n_1*n_2*n_3\) cells.Footnote 3 In cell \((i, j, k)\), we choose one cell, which has the minimum distance, from the seven neighboring cells and add the value to the distance value between three elements (\(x_i\), \(y_j\), and \(z_k\)). The DTW distance is obtained by accumulating these distances.

Definition 5

(Group-similarity) Given three sequences \(X\), \(Y\), \(Z\), and thresholds \(\varepsilon \) and \(l_{\min }\), the subsequences \(X[i_s:i_e]\), \(Y[j_s:j_e]\), and \(Z[k_s:k_e]\) have the property of group-similarity if they satisfy the following condition.

$$\begin{aligned} D(X[i_s:i_e], Y[j_s:j_e], Z[k_s:k_e]) \le \varepsilon (L(\!l_x,\! l_y,\! l_z) \!-\! l_{\min }).\nonumber \\ \end{aligned}$$
(11)

We compute the DTW distance among three sequences and detect the subsequences whose lengths are greater than \(l_{\min }\). As with cross-similarity, we face the overlap problem. The number of overlapping subsequences increases significantly with the number of sequences. We detect the best match of group-similarity as follows.

Problem 2

Given three sequences \(X\), \(Y\), and \(Z\), and thresholds \(\varepsilon \) and \(l_{\min }\), we want to find subsequences \(X[i_s : i_e]\), \(Y[j_s : j_e]\), and \(Z[k_s :\!k_e]\) that satisfy the following conditions.

  1. 1.

    \(X[i_s\!:\!i_e]\), \(Y[j_s\!:\!j_e]\), and \(Z[k_s\!:\!k_e]\) have the property of group-similarity.

  2. 2.

    \(D(X[i_s\!:\!i_e], Y[j_s\!:\!j_e], Z[k_s\!:\!k_e]) \!-\! \varepsilon (L(l_x, l_y, l_z)\!-\!l_{\min })\) is the minimum value from a set of overlapping subsequences that satisfies the first condition.

Let \(d_{i, j, k}(p, q, r)\) be the distance in cell \((p, q, r)\) in the time warping matrix for three sequences that starts from \(i\) on the \(x\)-axis, \(j\) on the \(y\)-axis, and \(k\) on the \(z\)-axis. The distance between the subsequences of \(X\), \(Y\), and \(Z\) can be obtained as follows. Footnote 4

$$\begin{aligned}&D(X[i_s:i_e],Y[j_s:j_e], Z[k_s:k_e]) = d_{i_s, j_s, k_s}(l_x, l_y, l_z)\nonumber \\&d_{i, j, k}(p, q, r) \!=\! ||x_{i+p-1} \!-\! y_{j+q-1}|| + ||y_{j+q-1} \!-\! z_{k+r-1}||\nonumber \\&\qquad \qquad \qquad \qquad + ||z_{k+r-1} \!-\! x_{i+p-1}|| + d_{\min } \end{aligned}$$
(12)

Note that \(d_{\min }\) is the minimum distance between the seven neighboring cells.

Lemma 6

The naive solution requires \(O(n_1w^3\!+\!n_2w^3\!+\!n_3w^3)\) time (per update) and space to discover the group-similarity for three sequences.

Proof

See Appendix 6. \(\square \)

How do we detect group-similarity with CrossMatch? We need only two matrices for computation (i.e., the score and position matrices). Each matrix has only two planes (i.e., previous and current planes) for each sequence \(X\), \(Y\), and \(Z\). For each incoming data point, we calculate \(O(w^2)\) score values and update \(O(w^2)\) starting positions. Specifically, given three sequences \(X\), \(Y\), and \(Z\) and warping scope \(w\), the score \(V(X[i_s\!:!i_e], Y[j_s\!:\!j_e], Z[k_s\!:\!k_e])\) of \(X[i_s\!:\!i_e]\), \(Y[j_s\!:\!j_e]\) and \(Z[k_s\!:\!k_e]\) is computed as follows.Footnote 5

$$\begin{aligned}&V(X[i_s:i_e], Y[j_s:j_e], Z[k_s:k_e]) = v(i_e, j_e, k_e)\nonumber \\&v(i, j, k) = \max (0, v_{best}) \end{aligned}$$
(13)

For cell \((i, j, k)\), we choose one of the seven neighboring cells and determine the score if the score \(v_{best}\) is not a negative value. For example, if the score of a diagonal cell \((i\!-\!1, j\!-\!1, k\!-\!1)\) is chosen, we have

$$\begin{aligned} v_{best}&= \varepsilon b_d - d_{cell} + v(i\!-\!1, j\!-\!1, k\!-\!1) \\ d_{cell}&= ||x_i - y_j|| + ||y_j - z_k|| + ||z_k - x_i|| \end{aligned}$$

where \(d_{cell}\) is the distance between the cells of the three sequences. While computing the score values, we update the starting position in the position matrix. If we choose one of the seven neighboring cells, we keep the same starting position. If not, we choose the current cell \((i, j, k)\) as the starting position. Thus, we can deal with the score computation and the updating of the starting position very effectively.

Lemma 7

Given three sequences \(X\), \(Y\), and \(Z\), Problem 2 is equivalent to the following conditions.

  1. 1.

    \(V(X[i_s\!:\!i_e],Y[j_s\!:\!j_e], Z[k_s\!:\!k_e]) \ge \varepsilon l_{\min }\)

  2. 2.

    \(V(X[i_s\!:\!i_e],Y[j_s\!:\!j_e], Z[k_s\!:\!k_e])- \varepsilon l_{\min }\) is the maximum value in each group of subsequences that the warping path crosses.

Proof

See Appendix 7. \(\square \)

From Lemma 7, Eq. (11) holds for any reported subsequences. As with Lemma 2, it is obvious that CrossMatch reports the optimal subsequences from the set of overlapping subsequences. Thus, CrossMatch guarantees the correctness of the result for group-similarity.

Lemma 8

CrossMatch requires \(O(w^2)\) time (per update) and \(O(w^2)\) space to discover the group-similarity for three sequences.

Proof

See Appendix 8. \(\square \)

Although the complexity of group-similarity is still quadratic with respect to the number of sequences, CrossMatch is much faster in practice than the naive solution and enables the examination of very large collections of sequences.

7 Experimental evaluation

We performed experiments to evaluate the effectiveness of CrossMatch. Our experiments were conducted on a 2.4 GHz Intel Core 2 machine with 4 GB of memory, running Linux. The experiments were designed to answer the following questions.

  1. 1.

    How well does CrossMatch provide the optimal subsequences without redundant information?

  2. 2.

    How successful is CrossMatch in capturing cross-similarity?

  3. 3.

    How effective is the sampling approach in capturing cross-similarity?

  4. 4.

    How well does CrossMatch scale with the sequence length in terms of computation time and memory space?

  5. 5.

    How well does CrossMatch work in high-dimensional data streams?

  6. 6.

    How well does CrossMatch identify group-similarity?

We used real and synthetic data sets for the experiments. These data sets (except high-dimensional sequences) are available for downloading from the web page.Footnote 6 The details of each data set are provided in the following subsections.

7.1 Filtering redundant information

We compared CrossMatch with the previous algorithm [66] to investigate its effectiveness in filtering redundant information.Footnote 7 We used a synthetic data set, Sines, which consists of discontinuous sine waves with white noise (see Fig. 8a), and for our previous algorithm and CrossMatch we set \(l_\mathrm{min}\) at 15 % of the sequence length, \(\varepsilon \) at \(1.0\times 10^{-2}\), and \(w\) at 50 % of the sequence length.

Figure 8b plots the sequence length versus the number of detected subsequence pairs for the two algorithms. In the previous algorithm, increases in sequence length trigger a large increase in the number of detected subsequence pairs. CrossMatch, on the other hand, detects fewer subsequence pairs than the previous algorithm.

Figure 8c shows how CrossMatch captures subsequence pairs. For visualization purposes, we find the optimal warping path by backtracking the selected cells from the end position and plot the cells from \((i_e, j_e)\) to \((i_s, j_s)\) for the subsequence pair \(X[i_s: i_e]\) and \(Y[j_s: j_e]\). Unlike the previous algorithm, CrossMatch provides only the optimal subsequence pairs in a streaming fashion. Therefore, by eliminating the overlapping subsequence pairs, the periodicity of cross-similarity is revealed and users can obtain ‘real’ results without receiving redundant information.

Fig. 8
figure 8

Effect of filtering redundant information. CrossMatch correctly outputs the best match of cross-similarity without redundant information

Full size image

7.2 Detecting cross-similarity between two sequences

We present case studies of real and synthetic data sets to demonstrate the effectiveness of our approach in discovering optimal subsequence pairs. We set \(l_\mathrm{min}\) at 500 for RandomSines and at 1,000 for Spikes in each synthetic data set. We set \(l_\mathrm{min}\) at 15 % of the sequence length for real data sets (i.e., Humid, Automobile traffic, Web, Sunspots, and Temperature). The warping scope \(w\) was set at 50 % of the sequence length for all data sets. The details of each data set and the settings for the experiments are given in Table 3. In Fig. 10, the left and center figures represent the data sets, and the right figures represent the optimal warping paths of cross-similarity detected from these data sets.

Table 3 Details of data sets and parameter settings
Full size table

7.2.1 RandomSines

We used a synthetic data set, RandomSines, which consists of discontinuous sine waves with white noise (see Fig. 9a). This data set includes different-length intervals between the sine waves, which were generated using a random walk function. We varied the period of each sine wave and the intervals between these sine waves in the sequence.

As shown in the right figure of Fig. 9a, CrossMatch perfectly identifies all the sine waves and their time-varying periodicities. In this figure, the difference in the period of each sine wave appears as a difference in the slope.

7.2.2 Spikes

This is the synthetic data set shown in Fig. 9b, which consists of large and small spikes. The data for different-length intervals between spikes were generated using a random walk function. The period of each spike is also different. As seen in the right figure of Fig. 9b, we confirm that CrossMatch detects both large and small spikes. The difference in the period of each spike appears as a difference in plot length; wide spikes indicate long plot lengths, and narrow spikes indicate short plot lengths.

Fig. 9
figure 9

Discovery of cross-similarity using Random Sines and Spikes. The left and center figures represent data sequences, and the right figures represent the optimal warping paths of cross-similarity

Full size image

7.2.3 Humidity

Figure 1 shows the detected subsequence pairs for the humidity data set. CrossMatch captures common patterns except for the dissimilar sections. Our method is designed to find the similar subsequence pairs. However, by applying it to sequences that are roughly similar, it can utilize the discovery of dissimilar sections.

7.2.4 Automobile traffic

Figure 10a shows time-series data of automobile traffic, which has a daily period. Each day contains other distinct patterns for the morning and afternoon rush hours. Hourly traffic is a bursty data, and we can regard it as white noise.

CrossMatch is successful in accurately detecting the daily period without being deceived by the high-frequency hourly traffic. Consecutive lines and their regular intervals indicate periodicity. Moreover, the intervals between the consecutive lines correspond to the daily period, and we can confirm that the characteristics of the data are revealed by the cross-similarity thus detected.

7.2.5 Web

Figure 10b shows access counts for mail and blog sites obtained every 10 seconds. We observe the daily periodicity of sequences, which increases from morning to night and reaches a peak.

The right figure in Fig. 10b confirms that CrossMatch identified the periodicity. The figure shows winding lines, unlike Automobile. This indicates that CrossMatch aligned the elements of sequences that were stretched along the time axis. Cross-similarity is detected by the time-scaling property of CrossMatch.

7.2.6 Sunspots

Figure 10c is sunspots data set recorded on a daily basis. This is a well-known data set whose time-varying periodicity is related to sun activity. The average number of visible sunspots increases when the sun is active and decreases when the sun is inactive. This change occurs with a regular period of about 11 years.

CrossMatch distinguishes the increase and decrease in the average number and captures similar periods.

7.2.7 Temperature

We use the temperature measurements (\(^\circ \text{ C}\)) from the Critter data set, which are obtained with small sensors (see Fig. 10d). The sensors give one reading approximately every minute. This data set has many missing values and the lengths of the two sequences are different. These sequences consist of similar changes with a temperature fluctuation of \(18\)–\(32^{\circ }\text{ C}\).

Fig. 10
figure 10

Discovery of cross-similarity using Automobile traffic, Web, Sunspots, and Temperature

Full size image

Despite the missing measurement values and the difference in the period, CrossMatch successfully detected the pattern.

7.3 Effect of sampling approach

In this section, we show the results we obtained with the sampling and adaptive sampling approaches. We used four real data sets for the experiment. To determine the sampling period for each data set in the sampling approach, we computed a power spectrum from the normalized sequences. Real data sets often include high frequencies with very low energy. The Nyquist frequencies for such data sets could be extremely high. Since the frequency limit is widely understood in various fields (e.g., audio processing and network analysis), in settings regarding Nyquist frequency, we disregard the high-frequency components, whose power is very small. We set the power value threshold at \(5.0\times 10^{-4}\) in this experiment. The main energy of Traffic #1 is distributed in the \(0 \! \le \! f \! \le \!1478\) frequency range and the Nyquist frequency is \(f_{N_q} = 2596/n\). Similarly, the main energy of Traffic #2 is distributed in the \(0 \! \le \! f \! \le \! 1438\) frequency range and the Nyquist frequency is \(f_{N_q} = 2876/m\). Thus, the sampling periods are \(T_x = 5\) and \(T_y = 6\).Footnote 8 With the adaptive sampling approach, the sampling rate varies depending on the frequency range.

Figure 11 presents the cross-similarity with the sampling approach. We omit the results we obtained with the adaptive sampling approach because they are almost the same as those of the sampling approach. The optimal subsequence pairs as well as those estimated in Fig. 10 provide an accurate assessment of the similarity between sequences. The original and sampling approaches offer very similar cross-similarity and are equally useful.

Fig. 11
figure 11

Discovery of cross-similarity with the sampling approach. The sampling approach correctly identifies the patterns as effectively as the original approach

Full size image

Next, we show the correctness of the results obtained with the two sampling approaches. We used the diarization error rate (DER) [26] to evaluate the accuracy. DER is a primary metric for speech recognition and presents the ratio of incorrect speech time against the total amount of exact speech time. In our evaluation, DER is represented by the ratio of the mismatch length to the exact subsequence length and is defined as follows.

$$\begin{aligned} DER_x&= \frac{|i_s - i^{\prime }_s| + |i_e - i^{\prime }_e|}{i_e - i_s+1} \\ DER_y&= \frac{|j_s - j^{\prime }_s| + |j_e - j^{\prime }_e|}{j_e - j_s+1} \end{aligned}$$

Note that \((i_s, j_s)\) is the exact starting position for the original CrossMatch  and \((i^{\prime }_s, j^{\prime }_s)\) is the approximate starting position for the two sampling approaches. The end positions are also the same. We calculate the DER for every detected subsequence pair and show their average values.

Table 4 gives the DER results. Although there are variabilities in each data set, the two sampling approaches closely identify the positions of optimal subsequence pairs. In particular, the DERs of the two approaches are different for Temperature. As compared with other data sets, which consist of high frequency, Temperature contains both of high and low frequencies. Therefore, it is considered that the algorithm approximates the score in response to the variation of the sampling period. As we expected, the adaptive sampling approach has an advantage as regards data sets that consist of high and low frequencies.

Table 4 Diarization error rate in two sampling approaches
Full size table

7.4 Performance

We compared two CrossMatch approaches (i.e., the original and sampling approachesFootnote 9) with the naive solution and an existing method, SPRING, in terms of computation time and memory space. SPRING detects high-similarity subsequences that are similar to a fixed length query sequence under the DTW distance [58]. SPRING is not intended to be used for finding cross-similarity, but we can apply this method to evaluate the efficiency and to verify the complexity of CrossMatch. SPRING requires \(O(n+m)\) matrices; thus, an algorithm with SPRING for finding cross-similarity requires \(O(nw+mw)\) time (per update) and space. We used Temperature for this experiment.

Figure 12 shows the experimental results with regard to computation time. This is the average processing time per time-tick for each sequence length. As we expected, CrossMatch identifies the optimal subsequence pairs much faster than the naive and SPRING implementations. The trend shown in this figure agrees with our theoretical discussion in Sect. 4.3.2. In particular, the sampling approach significantly reduces the computation time.

Fig. 12
figure 12

Wall clock time per time-tick as a function of sequence length. CrossMatch provides significantly better performance

Full size image

Figure 13 compares Naive, SPRING, and the two CrossMatch approaches in terms of memory space. The \(x\)-axis represents data stream length. The space requirement of CrossMatch is clearly lower than those of the Naive and SPRING implementations, and the sampling approach can greatly reduce the space requirement. The results also agree with our theoretical discussion in Sect. 4.3.2.

Fig. 13
figure 13

Memory space consumption as a function of sequence length. CrossMatch detects cross-similarity with a constant memory space

Full size image

7.5 Extension to high-dimensional data streams

We applied CrossMatch to high-dimensional data streams. One interesting problem is how to apply CrossMatch to motion capture data (see tables in Fig. 14). Mocap is a real data set created by recording motion information from a human actor while the actor performed different actions (e.g., walking, running, and kicking). Special markers are placed on the actor’s joints (e.g., knees and elbows), and their \(x\)-, \(y\)- and \(z\)-velocities are recorded at about 120 Hz.

Fig. 14
figure 14

Discovery of cross-similarity in Mocap. CrossMatch successfully detects the same motions (i.e., walking and jumping upward) in multidimensional sequences

Full size image

\(X\) and \(Y\) are multidimensional time sequences, and our goal is to find matching subsequences between \(X\) and \(Y\). Intuitively, if \(X\) and \(Y\) include the same motions, we want to find these motions.

We used sequences obtained from the CMU motion cap database.Footnote 10 We selected the data for limbs from the original data and used them as 8-dimensional data. Each motion is listed in the tables in Fig. 14. The data set has two motions in common (i.e., walking and jumping upward), and the length of each motion is different. We set \(l_{\min }\) at 240, which corresponds to about two seconds, \(\varepsilon \) at 10, and \(w\) at 50% of the sequence length.

The result shown in Fig. 14 reveals that CrossMatch can accurately capture the two motions. We can confirm that the walking motion yields high cross-similarity. There are many shifted sequences, because walking is a repetitive behavior in which the limbs move back and forth. CrossMatch works for high-dimensional data sets and detects the repetitive motion as cross-similarity.

7.6 Detecting group-similarity

We performed an experiment to discover group-similarity. We used the Sensor data set for this experiment (see Fig. 15). Sensor consists of three streams that represent temperature readings from sensors within several buildings. Each sensor provides a reading every 4 min. Overall, the data set fluctuates greatly at different time-ticks but the three sensors exhibit a similar fluctuation pattern.

We show the experimental result in the right figure of Fig. 15. The optimal warping path is plotted as a line in 3D space. CrossMatch discovers the fluctuation pattern in spite of the difference in the periodicity. In multiple sequences, providing a concise summary of key trends is a significant challenge. CrossMatch summarizes the three sequences into a manageable synoptic pattern and captures the characteristics shared by the sequences.

Fig. 15
figure 15

Discovery of cross-similarity in Sensor. CrossMatch captures a fluctuation pattern correctly

Full size image

8 Conclusions

We described the problem of finding common local patterns based on DTW over data streams and presented a practical solution. CrossMatch is a one-pass algorithm based on DTW, which detects local common patterns in constant time (per update) and space without sacrificing accuracy. A theoretical analysis and experiments demonstrated that CrossMatch works as expected. Furthermore, we have provided an enhancement, a sampling approach, to greatly compress the size of the matrices. We showed that the sampling approach further improves the efficiency of CrossMatch in terms of time and space requirements. CrossMatch has the following characteristics.

  • In contrast to the naive solution, CrossMatch greatly improves performance and can be processed at a high speed.

  • CrossMatch requires constant space (per update) to detect cross-similarity or group-similarity, and it consumes only a small quantity of resources.

  • Despite the high-speed processing, CrossMatch guarantees correct results.

  • CrossMatch works efficiently for high-dimensional data streams.

As a result, our detailed study provides many insights into the applicability and use of CrossMatch. In particular, CrossMatch proved crucial in producing significantly more concise and informative patterns, without any prior knowledge about the data.