Optimization of multiplane μPIV for wall shear stress and wall topography characterization

Abstract

Multiplane μPIV can be utilized to determine the wall shear stress and wall topology from the measured flow over a structured surface. A theoretical model was developed to predict the measurement error for the surface topography and shear stress, based on a theoretical analysis of the precision in PIV measurements. The main parameters that affect the accuracy of the measurement are identified. The effect of different parameter settings is studied by means of Monte Carlo simulations, and the results are compared with an experimental test case. The results are used to determine the recommended parameter settings for this measurement approach.

1 Introduction

The measurement of the motion of fluid near a surface can be used, under certain conditions, to determine the surface topography and the wall shear stress distribution over the surface. When the no-slip boundary condition is valid and there is no flow separation, the position of the wall corresponds to the point where the velocity vanishes. For Newtonian fluids, the wall shear stress is given by:

$$ \tau_{\text{w}} = \mu \left. {{\frac{{\partial u_{\text{n}} }}{\partial n}}} \right|_{z = h(x,y)} $$

(1)

where μ is the dynamic viscosity of the fluid, and ∂u _n/∂n is the gradient in the direction of the wall normal n of the velocity component parallel to the wall, which is located at a position h(x, y).

This approach may be desirable or even necessary in applications where a direct measurement of topography or wall shear stress is problematic or not possible at all. This includes, for example, applications in microfluidics and in biological flows, where techniques such as scanning electron microscopy (SEM), atomic force microscopy (AFM), or force sensing probes cannot be applied due to the construction of the microchannels or the fragility of the biological samples. Optical methods, like interferometry, that rely on reflective surfaces are difficult to apply in the case of biological materials.

On the other hand, the measurement of the velocity field in these cases can be relatively simple using whole-field velocimetry techniques such as micro-particle-image velocimetry (μPIV) (Santiago et al. 1998). Stone et al. (2002) demonstrated that it is possible to determine the shape of the wall of a microfluidic device with a resolution approaching tens of nanometers using μPIV measurements of the fluid motion near a surface. Poelma et al. (2008) used μPIV to determine the local wall shear stress in vivo in a repeatable manner. From the flow measurements, the wall shear stress was derived either directly from the magnitude of the gradients or from fits of an analytical expression to the measured velocity profiles. The application of μPIV to in vivo experiments presents practical problems due to the peculiarity of the object of investigation, i.e., a living organism. However, under particular conditions, e.g., when it is possible to have appropriate optical access and to introduce seeding particles, the measurement accuracy that can be achieved is comparable to analogous in vitro experiments (Vennemann et al. 2007; Poelma et al. 2009).

In this paper, we focus on the particular case when the topography and the wall shear stress distribution are derived from μPIV measurements taken in multiple planes parallel to the surface. For this purpose, two-dimensional velocity fields in N planes parallel to a surface are measured, starting from a plane close to the surface and moving toward the center of the channel (Fig. 1). In this way, we have for each (x,y) coordinate of the surface the corresponding velocity profile measured in N points. A second-order polynomial fit (Stone et al. 2002) is used to capture the shape of the measured velocity profile. The respective wall position corresponds to the root of the second-order polynomial (i.e., where the velocity vanishes), and the respective wall shear stress is extracted from the calculation of the velocity gradient in that point. In this case, the wall-normal velocity gradient in Eq. 1 is approximated to the velocity gradient along the z-direction ∂u/∂z. This approximation holds for surfaces with small wall inclination, and the following analysis will be restricted to this case. When the wall inclination is large, the out-of-plane velocity component has to be taken into account, e.g., by using a (multiplane) stereoscopic-μPIV system (Lindken et al. 2006).

Fig. 1

Determination of topography and shear stress distribution over a surface

The multiplane μPIV approach described here has already been used by several authors for in vitro cell adhesion studies (Lindken et al. 2009). Voorhees et al. (2007) used a similar procedure to show the importance of flow-induced pressure on the shape and alignment of endothelial cells. Recently, Rossi et al. (2009) used this approach to study the biochemical and biomechanical responses of endothelial cells cultured in microfluidic chips. A typical result obtained using this method is shown in Fig. 2, where the surface topography of a group of human endothelial cells in a microchannel was reconstructed from μPIV velocity measurements.

Fig. 2

a Fluorescent image of a group of human endothelial cells cultured in a microfluidic flow chamber. b Topography of the cellular layer surface reconstructed from μPIV velocity measurements. The aspect ratio of the z-axis with respect to the x- and y-axis is set to 5:1

Another possible application is the characterization of structures and surfaces in microfluidic devices. This approach was used by Joseph and Tabeling (2005) for the direct measurement of the apparent slip length in microchannels, and by Joseph et al. (2006) for the experimental characterization of liquid flow slippage over superhydrophobic surfaces made of carbon nanotube ‘forests’, incorporated in microchannels.

The topography and wall shear stress distribution are indirectly determined from the velocity measurement. The accuracy of the final result depends on a substantial number of interdependent parameters. In this paper, a model of the measurement method is described, and we use a Monte Carlo approach to optimize the performance of the system. The model is based on the theoretical analysis of the measurement precision in PIV developed by Keane and Adrian (1990, 1992) and Westerweel (2000, 2008). This paper intends to provide general guidelines for using this method or a similar approach.

The paper is structured as follows. First, the theoretical analysis is explained for the estimation of the error in the μPIV measurements (Sect. 2). This is used to perform a parametric optimization of the measurement method: first, the relevant parameters that affect the final result are identified, and subsequently, a Monte Carlo approach is used to analyze the effect of different parameter settings (Sect. 3). The conclusions of this study are discussed in the final section (Sect. 4).

2 Errors in μPIV for near-wall measurements

2.1 Theoretical analysis

μPIV is a technique derived from PIV (Adrian 1991; Westerweel 1997) that is used for the measurement of fluid velocity fields at microscopic scales (Santiago et al. 1998). The velocity fields are obtained by measuring the displacement of small tracer particles that follow the fluid motion. Two sequential digital images (or image pair) of the particles in the flow, separated by a known time interval Δt, are taken using a laser illumination source and an epi-fluorescent microscope. The image pairs are divided into small interrogation windows (IW), and a cross-correlation is performed in each IW between the first and the second image. The position of the correlation peak maximum gives the most likely in-plane displacement ΔX of the particles in the IW. The velocity u is given by:

$$ u = \Updelta X/M\Updelta t $$

(2)

where M is the image magnification and Δt the exposure time delay. Adrian (1988) and Westerweel (2000) demonstrated that the random error amplitude σ_ΔX in the measured displacement is approximately proportional to the diameter d _D of the displacement-correlation peak:

$$ \sigma_{{\Updelta {X}}} \approx c_{\tau } {\frac{{d_{\text{D}} }}{\sqrt 2 }} $$

(3)

where c _τ is a constant related to the experimental parameters (Westerweel 2000). For a uniform displacement of the tracer particles in the interrogation domain, the diameter of the correlation peak is $d_{\text{D}} \cong \sqrt 2 d_{{{\uptau}}}$, where d _τ is the mean particle-image diameter. (This expression is exact when the particle images have a Gaussian shape). The value of c _τ is typically around 0.05–0.1 (Adrian 1991; Boillot and Prasad 1996; Westerweel 2000).

As mentioned in the Sect. 1, we consider in this paper measurement planes parallel to a surface. This results in strong velocity gradients in the out-of-plane direction (i.e., normal to the measurement plane). Recently, it was shown that in the presence of velocity gradients, d _D is given by (Westerweel 2008):

$$ d_{\text{D}} \cong \sqrt {2d_{{{\uptau}}}^{ 2} + {\frac{4}{3}}a^{ 2} } \quad{\text{with}}\quad a \equiv M\left| {{{\Updelta}}u} \right|{{\Updelta}}t $$

(4)

where d _τ is the particle-image diameter, and Δu represents the local variation of the velocity field in the IW, i.e.:

$$ \left| {\Updelta u} \right|\sim \left| {\partial u/\partial z} \right| \cdot L $$

(5)

where L is a typical dimension of the interrogation volume, in this case (i.e., where the velocity gradient is in the out-of-plane direction) the thickness of the measurement volume. In μPIV, this thickness is typically defined in terms of the depth of correlation δ _corr. Meinhart et al. (2000a) define the δ _corr as twice the distance from the object plane to the nearest plane, in which a particle becomes sufficiently defocused so that it no longer contributes significantly to the measurement of the displacement. Olsen and Adrian (2000) derived the following expression for δ _corr :

$$ \delta_{\text{corr}} \cong 2\left[ {{\frac{(1 - \sqrt \varepsilon )}{\sqrt \varepsilon }}\left( {f^{{{\text{\# 2}}}} d_{\text{p}}^{ 2} + {\frac{{5.95(M + 1)^{2} \lambda^{2} f^{{{\text{\# 4}}}} }}{{M^{2} }}}} \right)} \right]^{ 1 / 2} $$

(6)

where d _p is the particle diameter, λ the light wavelength, M the image magnification, and ε the relative threshold below which the defocused particle images no longer contribute significantly to the displacement-correlation peak. Normally the value of ε is set to 0.01. f ^# is the f-number of the lens.

When the index of refraction of the working fluid is different from that of the immersion fluid of the lens, the actual value of the depth of correlation has to be modified. A correction factor k can be determined theoretically from Snell’s law and geometrical optics (Bown et al. 2006; Meinhart and Wereley 2003):

$$ k = \left( {{\frac{{n_{\text{w}}^{ 2} - {\text{NA}}^{2} }}{{n_{ 0}^{ 2} - {\text{NA}}^{2} }}}} \right)^{1/2} $$

(7)

where n ₀ is the refractive index of the immersion medium of the objective lens, n _w the refractive index of the working fluid, and NA = 1/(2f ^#) the numerical aperture of the objective lens. It also has to be noted that in presence of strong in-plane velocity gradients, the value of the depth of correlation may need to be adapted (Olsen 2009). In the following analysis, we neglect this latest effect, and consider measurements that are dominated by out-of-plane gradients of the velocity.

Now, assume that the observed flow is that of Poiseuille flow between two infinite parallel plates. This is generally valid for microchannels with rectangular cross-section and high aspect ratio that are typically used in cell adhesion experiments as well as in many microfluidic applications. Under this assumption, we have an analytical expression for the velocity u (and consequently the gradient ∂u/∂z) as a function of the distance z from the wall:

$$ u(z) = {\frac{{4V_{ 0} }}{{L_{ 0}^{ 2} }}}z\left( {L_{ 0} - z} \right) $$

(8)

where V ₀ is the maximum velocity at the center of the channel and L ₀ the channel height.

Provided that the particles accurately follow the flow and that errors due to the Brownian motion or shear-induced migration can be neglected (Wereley and Meinhart 2005), we can use Eqs. 2–4 and 8 to derive an analytical expression for the relative random error in the estimation of the particle-image displacement:

$$ {\frac{{\sigma_{{\Updelta {\text{X}}}} }}{\Updelta X}} \cong c_{{{\uptau}}} \cdot {\frac{{d_{{{\uptau}}} }}{\Updelta X}} \cdot \sqrt {1 + {\frac{2}{3}}F^{2} (z){\frac{{\delta_{\text{corr}}^{ 2} }}{{L_{ 0}^{ 2} }}}\,{\frac{{\Updelta X^{2} }}{{d_{{{\uptau}}}^{ 2} }}}} \,\,{\text{with}}\,\,F(z) = {\frac{{L_{ 0} {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}}}{u}} = {\frac{{1 - {{2z} \mathord{\left/ {\vphantom {{2z} {L_{ 0} }}} \right. \kern-\nulldelimiterspace} {L_{ 0} }}}}{{{z \mathord{\left/ {\vphantom {z {L_{ 0} - {{z^{ 2} } \mathord{\left/ {\vphantom {{z^{ 2} } {L_{ 0}^{ 2} }}} \right. \kern-\nulldelimiterspace} {L_{ 0}^{ 2} }}}}} \right. \kern-\nulldelimiterspace} {L_{ 0} - {{z^{ 2} } \mathord{\left/ {\vphantom {{z^{ 2} } {L_{ 0}^{ 2} }}} \right. \kern-\nulldelimiterspace} {L_{ 0}^{ 2} }}}}}}} $$

(9)

Equation 9 shows that the relative error is a function of the distance z from the wall and that it depends on three dimensionless terms, i.e.: ΔX/d _τ and δ_corr/L ₀, which are determined by the experimental parameters, and F(z), which depends on the flow velocity field. The mean displacement ΔX is determined by the exposure time delay Δt for the μPIV measurement.

2.2 Comparison with experimental results

μPIV measurements over a flat surface in a microchannel were performed to validate the expression in Eq. 9. A microchannel with a rectangular 0.127 × 2.5 mm² cross-section was used, in which a steady flow was applied of 0.8 ml/min. The wall shear stress and topography measurements were taken over a glass coverslip with a nominal roughness of less than 1 nm.

For the μPIV measurements, an inverted microscope (Axiovert 200, Zeiss) was used with an objective lens (LD Achroplan) with an image magnification of M = 63, a numerical aperture of NA = 0.75, and working distance of WD = 1.57 mm. This configuration yields a depth of field of 1.2 μm (Inoué and Spring 1997) and a depth of correlation of 4.5 μm, which has to be multiplied by the factor k defined in Eq. 7. Since the immersion fluid of the lens is air (n ₀ = 1), and the working fluid is water (n _w = 1.33), the factor k is equal to 1.66. The objective lens was mounted on a piezo-electric positioning device (MIPOS500SG, Piezosystem Jena GmbH) with a precision of 8 nm.

A high-performance double-frame camera with a 1,376 × 1,040 pixel-cooled CCD sensor (Imager Intense, LaVision) was used, with a pixel size of 6.45 × 6.45 μm² and a 12-bit dynamic range. The light source is a frequency-doubled, dual-cavity pulsed Nd:YAG laser (SoloPIV III, New Wave Research) with a wavelength of λ = 532 nm. Red fluorescent PEG-coated polymer microspheres with a diameter of 560 nm (Microparticles GmbH) were used as tracer particles. The fluorescent dye has a maximum absorption at a wavelength of 560 nm and a maximum emission at a wavelength of 584 nm. A LaVision FlowMaster system running DaVis 7.0 was used for the data acquisition and PIV evaluation. The vector fields were obtained by means of a multi-pass cross-correlation algorithm with a final interrogation windows size of 128 × 128 pixels, with 50% overlap between adjacent interrogations, yielding a final grid of 21 × 16 vectors. No image preprocessing was applied. Vector postprocessing was used to reject possible outliers. Measurement planes were taken at different heights according to the configuration settings, as it will be later explained in the results section. The exposure time delay Δt was set to have a mean pixel displacement in each measurement plane of 12 pixels. The experimental settings are summarized in Table 1.

Table 1 Experimental settings

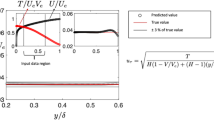
A total of 2,000 valid velocity vectors in each measurement plane were taken, which corresponds to 2,000 independent measurements. The random error in the velocity measurement as a function of the distance of the measurement plane from the wall is shown in Fig. 3. The analytical expression in Eq. 9 was used to fit a curve through the experimental data using the constant c _τ as a fitting parameter. We thus found a value of c _τ  = 0.095.

Fig. 3

Random error amplitude σ _ΔX in the measured displacement as a function of the distance z from the channel wall, relative to the channel height L ₀. Comparison between experimental data and the analytical solution from Eq. 9 with c _τ = 0.095

3 Parametric optimization

3.1 Relevant parameters in the optimization

The topography and wall shear stress distribution are derived from the measurement of the velocity flow field over the surface performed by μPIV as described previously. The measurement error in the measured particle-image displacement (viz., velocity) is considered to be the main contribution to the total error. Most of the parameter settings affecting the precision of μPIV measurements are constrained by the experimental setup, such as the f-number (expressed in terms of the numerical aperture NA for microscope lens), the image magnification of the optical system, and the diameter and concentration of the tracer particles. The correct choice of these parameters has been described extensively in the literature (Keane and Adrian 1992; Westerweel 1997; Raffel et al. 1998) and will not be further described in this work. Once the experimental parameters are fixed, as we have shown in the previous section, the error in the velocity measurement can be considered as a function of the exposure time delay Δt and the distance z of the measurement planes from the wall. For each measurement plane, we can select a separate exposure time delay, i.e., Δt = Δt(z). In this paper, we consider two different strategies for setting the Δt, which will be further evaluated in the Monte Carlo simulation:

• (a) Δt is chosen as to keep the mean particle-image displacement ΔX constant in each plane;

• (b) Δt is chosen as to keep the displacement error σ_ΔX constant, i.e., a = constant; c.f. Eq. 4

Figure 4a shows the trend of the relative error as a function of z when these two different strategies are adopted. Keeping σ_ΔX constant, i.e., a = constant, leads to larger errors in the planes closest to the wall, but the error decreases faster for increasing distance from the wall. A strong limitation for this second strategy is given by the large displacement required to maintain a constant σ_ΔX as the distance from the wall is increased, as shown in Fig. 4b. In fact, the particle-image displacement should not exceed about one-quarter of the size of the IW to avoid significant loss-of-correlation (Keane and Adrian 1992), although it is possible to compensate for large in-plane displacements by adopting window-offset interrogation.

Fig. 4

The effect of choosing an exposure time delay to either maintain a constant particle-image displacement or a constant velocity variation a in all planes. a Relative error versus distance from the wall; b Displacement versus distance from the wall

With regard to the positioning of the measurement planes, we identified the following parameters that contribute to the precision of the final result represented in Fig. 5:

Fig. 5

Multiplane measurement configuration: Δz is the spacing between planes, δ _corr the depth of correlation, and L the height of the measurement volume

• the number N of measurement planes;

• the spacing Δz between subsequent planes;

• the total height L of the measurement volume.

The number N of measurement planes corresponds to the number of measurement points in each velocity profile. A parabolic curve fitting requires a minimum number of three data points (viz., planes). Increasing the number of data points improves the quality of the curve fit, but it also increases the quantity of the stored data and the total computational effort. The distance between planes Δz defines how dense the measured velocity components are determined in each vertical velocity profile. A small distance Δz between planes improves the spatial resolution of the measured velocity profile. On the other hand, owing to the relatively large thickness of the measurement planes (defined by the correlation depth δ _corr), a significant overlap occurs for Δz ≪ δ _corr. This implies that adding more planes means that only statistically correlated data are included in the curve fitting, which does not further improve the quality of the curve fit. The height L of the overall measurement volume is the distance between the wall and the top boundary of the upper measurement plane. Evidently, N, Δz, and L are interdependent of each other, and we can deduce one of them from the other two using the relation:

$$ L = \delta_{\text{corr}}^{{}} + (N - 1)\Updelta z $$

(10)

We set the distance of the first plane, which is the closest to the wall, to a fixed position at half the thickness of the measurement plane (i.e., correlation depth); see Fig. 5. Closer to the wall the measurement volume penetrates into the wall, and a bias occurs on the velocity measurement that will affect the estimation of the wall position and wall shear stress.

We do not take into account possible errors in the positioning of the plane, assuming that most of the traversing systems used to move the objective lens are accurate enough to neglect this source of error.

In conclusion, we can reduce the optimization to the following three main parameters:

• (1) the exposure time delay Δt;

• (2) the height L of the measurement volume;

• (3) the number N of measurement planes.

3.2 Monte Carlo simulations

We used a Monte Carlo method (Morgan 1984) to study how the three parameters defined in the previous paragraph influence the accuracy of the final result. Equation 8 is used to generate a velocity profile according to predefined settings of L and N. A random variation is applied to each velocity vector using the corresponding standard deviation obtained from Eq. 9 for a chosen Δt. From the generated velocity profile, the position of the wall h and the wall shear stress τ are extrapolated. The iteration of this procedure gives the mean values and the standard deviations of h and τ that can be achieved with the chosen parameter settings. We also evaluated the correlation of the estimates for h and τ.

Two different recording strategies for setting the Δt were adopted:

• Simulation 1 with Δt chosen in such a manner to keep the displacement ΔX constant in all planes and

• Simulation 2 with Δt chosen to keep the variation a of the displacement in the interrogation volume constant in all measurement planes (i.e., this implies a constant error amplitude σ_ΔX in all planes; see Eq. 4).

We used non-dimensional quantities defined as follows:

$$ \begin{array}{*{20}c} {l = L_{0} \tilde{l}} & {(l = {\text{ML}}_{0} \tilde{l})} & {u = V_{0} \tilde{u}} & {t = {\frac{{L_{0} }}{{V{}_{0}}}}\tilde{t}} & {\tau = \tau_{0} \tilde{\tau }} \\ \end{array} $$

(11)

where l represents length or distance (e.g., the height L of the measurement volume or the position of the wall h), L ₀ the channel height, V ₀ the maximum velocity, and τ₀ the nominal wall shear stress. The results are discussed below.

3.2.1 Simulation 1

In Fig. 6, the mean value and standard deviation of h and τ, respectively, are plotted as a function of the mean particle-image displacement (here presented in terms of ΔX/IW) evaluated for three different values of L and with a constant number of N = 8 measurement planes. The simulations show that low values of ΔX lead to an overestimation of h and τ. The standard deviations of h and τ also increase as ΔX is decreased. In general, apart from the case for L = 0.15, where the height of the measurement volume is probably too small, particle-image displacements larger than about 0.12 the IW size (corresponding to a displacement of 15 pixel) no longer contribute to a significant improvement of the measurement result.

Fig. 6

Mean value and standard deviation of h and τ as a function of the constant mean particle-image displacement ΔX/IW in all measurement planes for three values of the height L of the measurement volume. In all cases, the number of measurement planes is constant: N = 8. The size of IW in the simulations was 128 pixel

It can be noticed that h for large displacements and large L converges to a value less than zero, while one may expect h to converge to zero. Although we presently do not have an explanation for this effect, it is rather small, since the deviation from zero is one order of magnitude smaller than the random error.

In Fig. 7, the results are shown for a simulation in which L is varied. In this case, the particle-image displacement was kept constant to a value of 0.09 times the IW size (corresponding to 12 pixel for our measurements), and the simulation was performed for three different values of the number N of measurement planes. As can also be observed in Fig. 6, small values of L lead to an overestimation of h and τ. The simulation results show that the height of the measurement volume should be about 30% of the channel height (or other characteristic length scale that describes the velocity profile) to avoid significant bias errors. Large values of L are also favorable to decrease the random error amplitude in the estimation of the wall shear stress τ. In particular, the random error amplitude shows a rapid increase with L when the height of the measurement volume becomes less than 0.2 times the channel height. On the contrary, a weak dependence on L is observed for the random error amplitude of h, which remains nearly constant.

Fig. 7

Mean value and standard deviation of h and τ, respectively, as a function of the height L of the measurement volume for three values of N. In all cases, the mean particle-images displacement is constant with ΔX/IW = 0.09 (corresponding to 12 pixel units for IW = 128 pixel)

Finally, the effect of the variation of the number N of measurement planes is reported in Fig. 8. In this case, the particle-image displacement was kept constant at 0.09 times the IW size (corresponding to a displacement of 12 pixel in our measurements), and the simulation was performed for three different values of L. The simulation shows that a larger number of planes can slightly improve the accuracy of the final result, but this parameter appears to play a minor role in comparison with the variation of the other parameters. It should be noted that varying the number N of measurement planes for a constant value of L means that the distance Δz between the measurement planes also varies, as shown in Eq. 10. Thus, the graphs in Fig. 8 also show that a variation in the separation between planes does not significantly affect the accuracy of the final result.

Fig. 8

Mean value and standard deviation of h and τ, respectively, as a function of number N of planes for three values of the height L of the measurement volume. In all cases, the mean particle-image displacement is constant in all measurement planes: ΔX/IW = 0.09 (corresponding to 12 pixel units for IW = 128 pixel)

3.2.2 Simulation 2

In Fig. 9, the mean value and standard deviation of h and τ, respectively, are plotted as a function of the variation a = M|Δu|Δt of the particle-image displacement within the interrogation volume (here a is normalized with the particle-image diameter d _τ). The simulations show that a small value of a increases the error in the estimation of h and τ. However, with a larger than 1–1.5 times d _τ, the standard deviation of h and of τ does not show any further significant decrease. The increase of a is anyhow limited by the corresponding large particle-image displacement required in the planes most distant from the wall (where the velocity gradient becomes very small), as discussed before. Taking this into consideration, a value of a/d _τ ≈ 1 can be considered as a suitable compromise between reducing the estimation errors and limiting the particle-image displacements within reasonable bounds.

Fig. 9

Mean value and standard deviation of h and τ, respectively, as a function of the variation a = M|Δu|Δt of the particle-image displacement within the interrogation volume relative to the particle-image diameter d _τ for three values of the height L of the measurement volume. In all cases, the number N of measurement planes is equal to N = 8

Analogous results are obtained for the parameters L and N in the case of Simulation 1. A minimum value of L > 0.25–0.30 times the channel height is required to maintain control on the magnitude of the error in the estimation of h and τ and to avoid any significant bias errors; see Fig. 10. Figure 11 shows that increasing the number of planes does not significantly improve the quality of the measurements.

Fig. 10

Mean value and standard deviation of h and τ, respectively, as a function of the height L of the measurement volume for three values of the number N of measurement planes. In all cases, the variation a of the displacement in the interrogation volume is constant: a/d _r = 1

Fig. 11

Mean value and standard deviation of h and τ, respectively, as a function of the number N of measurement planes for three values of the height L of the measurement volume. In all cases, the variation a of the displacement in the interrogation volume is constant: a/d _r = 1

Given the simulation results in Figs. 6–11, it can be concluded that:

• (1) A minimum height of the measurement volume is required to keep the bias error and the random error for the estimates of h and τ within acceptable limits. For the channel flow configuration we chose, this is around 0.25–0.3 times the channel height;

• (2) Increasing the number of measurement planes does not significantly improve the quality of the estimates for h and τ;

• (3) The two strategies investigated to set the exposure time delay Δt in each plane give similar results. When the exposure time delay Δt is set to have constant variation a of the particle-image displacement in all measurement planes, a value of a/d _τ ≈ 1–1.5 is advised. Although the two strategies show similar results, the second one is limited by the larger particle-image displacements obtained in the planes most distant from the channel wall as the value of a is increased.

3.3 Comparison with experimental results

To validate the results of our Monte Carlo simulations, measurement data obtained in the experiment presented in Sect. 2.2 are used to determine the mean value and standard deviation of the estimates for h and τ with different settings for the height L of the measurement volume and the number N of measurement planes. Since we take measurements in a channel with smooth and parallel walls, we expect that the actual values for h and τ are constant at all (x, y) locations.

The results obtained from the experimental data are shown in Fig. 12 together with the corresponding results from the Monte Carlo simulations. In this case, the distance from the wall of the first measurement plane was extrapolated from the experimental data and corresponds to 1.5 μm. The experimental results show a good agreement with the performance predicted from the Monte Carlo simulations.

Fig. 12

Mean value and standard deviation of h and τ, respectively, as a function of the height L of the measurement volume for two values of the number N of measurement planes. Comparison of experimental results versus results from Monte Carlo simulations for the case of maintaining a constant mean particle-image displacement in all measurement planes

The measured values of the surface height h and wall shear stress τ are positively correlated, i.e., an experimental error that leads to an increase in h leads to an increase in the estimated wall shear stress τ, and vice versa. In Fig. 13a, the correlation plot of the measured values for h and τ in the flow measurements over a flat channel wall is presented. The plot represents a measurement with L = 0.3 times the channel height and N = 8 measurement planes. With this configuration, we were able to measure the channel wall position h with a 95% confidence interval of ±1.4 μm and a wall shear stress τ of 2 Pa with a 95% confidence interval of ±0.5 Pa. It is observed that the errors in the determination of h and τ are correlated with a correlation coefficient of 0.57. The estimates of h and τ for the same configuration obtained from the Monte Carlo simulation are plotted in Fig. 13b. The comparison of the two graphs confirms that the simulation results provide a decent prediction of the accuracy for the actual experimental data. The correlation between surface height h and wall shear stress τ is considered to be weak (with a correlation coefficient of about 0.6), but not negligible.

Fig. 13

Correlation plots of the measured values for h and τ in experimental data (a) and Monte Carlo simulation (b). The plots correspond to the case in which L = 0.3 times the channel height and N = 8 measurement planes

Finally, we show in Fig. 14a the correlation plots of h and τ for the measurement of the endothelial cell layer presented in Fig. 2 in comparison with a measurement taken with the same configuration over a flat wall (Fig. 14b). It is noted that in this case, the μPIV measurements were taken using correlation averaging (Meinhart et al. 2000b; Wereley and Meinhart 2005) over 200 image pairs. This leads to smaller errors in the velocity measurement and in the estimate of the confidence intervals for h and τ equal to ±0.3 μm and ±0.1 Pa, respectively. From the two graphs in Fig. 14, it is clearly visible that, in the presence of a structured surface, the variation in wall shear stress is mainly correlated to the variation in height of the cellular layer. The slightly different trends that can be observed in Fig. 14a are due to the fact that the graph includes the measurement over a group of five distinct cells with different elevations and shapes.

Fig. 14

Correlation plots of h and τ for the measurement over an endothelial cell layer (a) presented in Fig. 2 and (b) a measurement taken with the same configuration over a flat wall

4 Summary and conclusions

In this paper, we present how to optimize a measurement approach that uses μPIV measurements to determine the topography and wall shear stress distribution over a surface. Such measurements are relevant in studies of the response of endothelial cells to flow shear stress and in the assessment of structured surfaces in microfluidic devices. The topography and wall shear stress are determined from the velocity of the flow over the surface, measured in several planes parallel to the surface. Three relevant parameters for the accuracy of final result have been identified: the height L of the measurement volume, the number N of measurement planes, and the exposure time delay Δt (for each measurement plane) in the μPIV measurements. How the choice of these parameters modifies the final result was investigated by means of a Monte Carlo method. The theoretical result for the random error amplitude in the μPIV measurement as a result of velocity gradients in the interrogation volume (in particular in the out-of-plane direction) has been used to predict the random error amplitude in the velocity measurements in each measurement plane.

In general, the results show that a minimal height L of the measurement volume is required to maintain bias errors and random errors in the estimates for the surface height h and wall shear stress τ within acceptable limits, while the number N of measurement planes does not play a significant role in the accuracy of the final results. The minimum height needed depends on the experimental configuration (i.e., the magnification and numerical aperture of the objective microscope lens, and the characteristics of the PIV evaluation). This minimum height should be about 0.3 times the channel height (or other characteristic length of the velocity profile in other flow geometries) as studied in this work. With regard to the effect of the exposure time delay Δt for each measurement plane, two strategies were investigated: Δt set to keep the mean particle-image displacement constant and Δt set to keep the variation a of the particle-image displacement constant. In the first case, simulations show that a large value of ΔX is desirable (i.e., typically ΔX/d _τ > 1). In the second case, a large value of a is desirable as well, in this case larger than 1–1.5 times the particle-image diameter, although it has to be taken into account that large values of a may also produce very large particle-image displacements in the planes most distant from the wall. Results obtained in an actual experimental configuration confirm the findings of the Monte Carlo simulations.