Coherent manipulation of trapped Rb atoms by overlapping frequency-chirped laser pulses: theory and experiment

Abstract

We present results of experimental and theoretical studies of coherent momentum transfer to rubidium atoms in a magneto-optical trap by pairs of counter-propagating frequency-modulated (chirped) laser pulses. The counter-propagating pulse pairs partially overlap each other leading to multiphoton interaction processes. We show experimentally that the mechanical momentum transferred to atoms in this scheme of interaction is larger than in the case of non-overlapping pulse pairs acting separately on the atoms. Results of numerical simulations that take into account all relevant hyperfine energy states of Rb along with the influence of relaxation and re-pumping processes are in good agreement with obtained experimental results.

Graphical abstract

1 Introduction

Coherent manipulation of atomic (molecular) ensembles without heating them is a central problem to be solved in all experimental studies and applications where conservation of the atomic phase is a crucial issue. It is the case, for example in atomic interferometry (see, e.g., [1,2,3,4,5], as well as review papers [6, 7] with references therein), in the transportation of atomic ensembles between different steps of laser-cooling systems, (for example during the creation of Bose–Einstein condensates), [8, 9] and many other fields of science and technology.

A powerful scheme of coherent manipulation of the mechanical states of atoms is stimulated Raman adiabatic passage (STIRAP) whose important advantage is that the atomic population transfer between ground states in $\varLambda$-structured atoms takes place without considerable excitation of the atom. The coherence of the interaction is thus preserved [10] and the scheme is useful in state-of-the-art manipulation schemes [11, 12]. The population transfer is achieved using two partially overlapping laser pulses (pump and Stokes) in a counter-intuitive sequence. They provide adiabatic following of a dark superposition of the ground states that contains no intermediate excited state probability amplitude [6, 7]. Since the transfer of the atomic populations takes place through a two-photon (Raman) absorption-emission process, mechanical momentum equal to $\hbar \left( \overrightarrow{k_{p}}-\overrightarrow{k_{s}}\right)$ will be transferred to the atom, where $\overrightarrow{k_{p}}$ and $\overrightarrow{k_{s}}$ are wave vectors of the pump and Stokes waves. Consequently, the atom will receive a mechanical momentum equal to $\hbar \left( k_{p}+k_{s}\right)$ when the STIRAP pulses are counter-propagating. While the preservation of the atomic coherence is an important inherent property of STIRAP, the overall value of the transferred mechanical momentum to atomic beams is limited due to the Doppler shift induced by the variation of the atomic velocity during the momentum transfer [6, 7]. There are also other schemes of the coherent manipulation based on the recoil technique in a standing wave geometry, (see [8, 13,14,15,16,17]). In these schemes, a large frequency detuning should be applied to suppress excitation of atoms and preserve the atomic coherence. The large frequency detuning, however, may significantly decrease the interaction efficiency.

Strong cooling/accelerating forces can also be induced by counter-propagating frequency-modulated continuous beams as in the case of the sawtooth-wave adiabatic passage (SWAP) technique [18]. The frequency of the radiation is modulated in a sawtooth pattern over the transition frequency where the slow upward ramp fulfills the adiabatic conditions but the fast downward ramp is diabatic. Efficient cooling of a precooled atomic ensemble has been demonstrated using a dipole-forbidden transition of strontium [19]. The same method can also be applied for the preparation of a magneto-optical trap [20]. This method is especially useful for inducing strong stimulated forces on atomic or molecular species with a narrow linewidth or lacking a cycling transition.

Another important scheme for the efficient transfer of mechanical momentum from light to atomic ensembles is based on stimulated excitation and de-excitation of atoms by counter-propagating laser pulse pairs [21]. The scheme may be easily described on a two-level model atom. If a laser pulse excites the atom, the latter acquires mechanical momentum equal to that of the absorbed laser photon $\hbar \overrightarrow{k_{L}}$ ($\overrightarrow{k_{L}}$ being the wave vector of the laser pulse). A subsequent laser pulse similar to the first one but propagating in the opposite direction will de-excite the atom to its ground state resulting in the atom receiving a recoil momentum equal to $\hbar \overrightarrow{k_{L}}$. Overall, the atom will receive a mechanical momentum equal to $2\hbar \overrightarrow{k_{L}}$ after interacting with the pair of counter-propagating laser pulses. The method requires that each pulse transfers the atomic population with close to a hundred percent probability. This can be achieved by using $\pi$-pulses or frequency-chirped (FC) laser pulses that transfer population in the adiabatic passage (AP) regime [21,22,23]. Of course, the duration of the pulses and the time interval between them have to be much shorter than the relaxation time of the atomic system to avoid the spontaneous decay of the excited state and to preserve the coherence. Adiabatic passage can be used effectively to implement the method for more complicated, multilevel atomic [6, 7, 24, 25] or molecular [26] systems as well. It is worth noting that the cycle of excitation and de-excitation resulting in the transfer of $2\hbar k_{L}$ momentum can be repeated at a high rate, so the overall force on the atoms or molecules can greatly exceed the light pressure force mediated by excitation spontaneous-emission cycles [26,27,28,29,30].

It has been suggested in theoretical works that the momentum transfer to a two-level atom by a pair of counter-propagating laser pulses may be significantly increased if the pulses are not acting separately but partially overlap each other when interacting with the atom [31, 32]. In Ref. [31], counter-propagating, partially overlapping pulses with constant (non-equal) frequencies detuned from the atomic resonance were considered. A similar scheme of counter-propagating (retro-reflected) pulses but with linearly chirped carrier frequencies was considered in Ref. [32]. In both cases, a possibility of the coherent transfer of $2n\hbar k_L$ momentum (with $n>1$ being an integer) to the atoms by a single pulse pair was shown theoretically. This effect may be explained in terms of adiabatic quasi-energies in momentum space. The atom can be adiabatically transferred from its initial momentum state to a final state characterized by a momentum value of $2n\hbar k_L$ with a probability value depending on the peak intensity of the pulses and the delay between them. A nonlinear multiphoton interaction of the atom with the overlapping counter-propagating laser pulse pair takes place: the atom with some probability may virtually absorb n photons from one laser pulse and emit n photons into the counter-propagating pulse gaining a momentum equal to $2n\hbar k_L$. The original scheme of non-overlapping, counter-propagating pulses can be thought of as the $n=1$ ‘small overlap limiting case’ of the multiphoton process.

While the theory of this multiphoton process is well developed and the underlying physics understood, an experimental confirmation of this effect has not yet been provided. It is evident however that implementation of such an efficient scheme of mechanical manipulation of atoms (molecules) may significantly improve the techniques utilized in atomic interferometry and other fields of science where efficient transportation of atomic or molecular ensembles is needed without disturbing the coherence of the systems. This technique may also find applications in atomic (molecular) lithography, as well as for the capture of atoms or small particles in an optical trap [33].

In this paper, we present a theoretical and experimental analysis of the momentum transfer to an ensemble of Rb atoms initially collected in a magneto-optical trap (MOT) in the field of counter-propagating and partially overlapping laser pulses with frequency chirp. Numerical simulations are performed using a theory that takes into account the full structure of the hyperfine energy levels of the $\mathrm {D}_2$ line of the $^{85}\mathrm {Rb}$ atoms (see Fig. 1), spontaneous relaxation processes and optical pumping of the atomic population. The laser pulse parameters are taken in the simulations as close as possible to the ones used in the experiment and theoretical predictions are compared with experimental results.

Fig. 1

Structure of the hyperfine levels of the $^{85}\mathrm {Rb}\;\mathrm {D}_{2}$ transition. The spacings are not shown to scale between the manifolds

2 Experiment

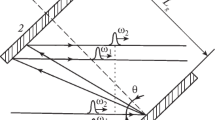
The multiphoton adiabatic acceleration experiments were carried out on $^{85}\mathrm {Rb}$ atoms initially collected in a magneto-optical trap of the conventional arrangement [34,35,36,37,38] (see Fig. 2). The vapor of rubidium atoms was produced using an alkali metal dispenser (SAES Getters). The trapping optical force was generated by an external cavity diode laser (ECDL; type EOSI-2001) tuned 10 MHz below the $5\mathrm {S}_{1/2}\,F=3 - 5\mathrm {P}_{3/2}\,F'=4$ hyperfine transition. Re-pumping ($F=2 \rightarrow F'=3$) was provided by a laser diode (Sanyo DL-7140), and both lasers were frequency stabilized to the respective transitions by saturated absorption technique. The retro-reflected beam of a frequency-chirped diode laser system was directed at the atomic cloud at a small angle with respect to one of the horizontal MOT laser beams. The beam was focused to produce a spot diameter of about 0.7 mm at the MOT, overlapping the atomic cloud. The waist of the focused laser beam was actually placed on the reflecting mirror in order to achieve the same spot size in the forward and backward propagating beams. The laser beam after passing the MOT cloud was deflected by a wedge and then reflected back by a mirror, providing the backward propagating laser beam. The forward and backward propagating beams crossed each other at the MOT cloud at a small angle so that back-reflection of the beam into the laser could be avoided. The distance of the mirror from the MOT cloud was about 45 cm so the delay time between the forward and backward propagating pulses was about 3 ns.

Fig. 2

Schematic upper view of the experimental arrangement. M and QW represent ‘mirror’ and ‘quarter wave plate,’ respectively. Some technical details (e.g., the vertical MOT and re-pumping laser beams, the anti-Helmholtz coils and the deflection of the chirped laser beam by a wedge) are omitted for simplicity

Frequency-chirped laser pulses with duration in the nanosecond range were generated by slicing pulses from the continuous wave (CW) radiation of the current-modulated diode laser using electro-optical modulators. The appropriate frequency modulation was adjusted by the parameters of the sinusoidal modulation of the driving current of the laser diode (Sanyo DL-7140) operating at 780 nm wavelength. A modulation frequency of 16.7 MHz was chosen so that the delay time between the consecutive pulse pairs (60 ns) was longer than the decay time of the excited Rb atoms (26.2 ns), but at the same time, the repetition rate was high enough to ensure an efficient interaction. The chosen value of the repetition rate was a compromise between conflicting requirements and not ideal for this kind of experiment, it was the result of an optimization procedure to observe maximum acceleration of the atomic cloud.

The pulses were cut out from the CW radiation by integrated lithium-niobate amplitude modulators of Mach–Zehnder interferometer setup. In order to reach high enough intensity contrast of the pulses, two modulators were used in series. It is known that certain kinds of (viz. Z-cut) electro-optical intensity modulators can introduce residual chirp [39, 40], which is proportional to the time derivative of the control voltage, i.e., it is most pronounced at the steep sloping edges of the pulses. One of our modulators (Eospace AZ-0K5-10-PFU-PFU-780) has this property, while the other one (Photline NIR-MX800-LN-10), being X-cut, is free of chirp. These modulators were controlled with two different pulse generators by opening the chirp-free modulator for a shorter period, thereby blocking the potentially chirped light from the Z-cut modulator during the steep sloping edges of the pulses. As a result, we could not observe any frequency chirp introduced by the pair of modulators by interference measurements on the output laser pulses.

The pulses were then amplified by diode laser amplifiers (Toptica BoosTA) to a peak intensity of up to about 100 W/cm$^2$ necessary to reach the adiabatic interaction regime. Pulse trains consisting of about 5000 pulses were chopped by a mechanical shutter made from an electric relay.

The frequency evolution of the modulated laser radiation was monitored during the experiments by measuring its interference with the frequency stabilized beam of the ECDL operating the MOT [41]. This beat signal was detected by a fast photodiode (New Focus 1591NF; 4.5 GHz bandwidth) and recorded by a digital oscilloscope (Tektronix DPO7354; 3.5 GHz bandwidth). The interference signals registered together with the pulse shapes and timings were evaluated by curve fitting procedures for each shot and so the parameters of the frequency sweep during each pulse train were calculated. Therefore, the frequency dependence of the phenomena could be investigated with a fairly high resolution. The frequency evolution during the pulses, obtained from the evaluation process, is illustrated in Fig. 3 for a particular set of modulation parameters.

Fig. 3

Frequency evolution during the laser pulse, obtained from the evaluation process for a particular set of modulation parameters. The dashed (blue) line represents the sinusoidal frequency evolution, calculated by the fitting procedure. Zero frequency denotes the resonance frequency of the rubidium transition $5\mathrm {S}_{1/2}\,F=3 - 5\mathrm {P}_{3/2}\,F'=4$. The pulse shape [solid (red) line] is fitted to the measured signal assuming rise and fall sections described by ${\textit{Erf}}$-functions; the actual pulse duration (FWHM) is 7.74 ns in this case. The frequency range swept by the laser is $+145.7$ MHz $\rightarrow$ $-349.5$ MHz during this pulse

Fig. 4

Pictures of the atomic cloud taken with the intensified CCD camera (average of 20 shots); a original MOT, b accelerated from 1 direction and c accelerated by the overlapping counter-propagating pulse pairs

The acceleration of the atomic cloud was recorded by image intensified CCD cameras which were triggered with an appropriate delay (about 160 $\upmu$s) with respect to the start of the pulse train. The exposure length of the CCD camera was set to about 100–140 $\upmu$s, that is, an integrated image of the acceleration of the MOT cloud was taken during a few thousand pulse pairs. In Fig. 4, typical images of the atomic cloud can be seen without and with acceleration by the chirped pulse sequences. Since unfortunately our image intensifier could not be operated in gated mode, the exposure time was determined by the CCD camera, resulting in blurred images of the moving atomic cloud during the exposures, thereby limiting the resolution of the measurements. The re-pumping laser radiation of the MOT system was continuously switched on in order to repump atoms from the lower ground hyperfine level to the upper one. However, the main laser beams constituting the MOT effect were shut off about 150 ${\upmu }$s prior to the start of the chirped laser pulse train, so that no restoring force of the MOT on the atoms could interfere with the acceleration due to the adiabatic transfer processes.

The obtained CCD image data were evaluated by assuming a uniform acceleration of a cloud of atoms with a Gaussian distribution in space. The finite integration time during the acceleration was taken into account by numerical integration of the accelerating Gaussian distribution. The intensity distribution of the integrated image of the Gaussian atomic cloud accelerating in the x direction can be described as:

$$\begin{aligned} I(x,y) = A \int ^{t_2}_{t_1} \exp \left( {{({x-x_0+a t^2/2})^2 \over {2 \sigma _x ^2}} + {({y-y_0})^2 \over {2 \sigma _y ^2}} }\right) \mathrm{d}t \end{aligned}$$

(1)

where $x_0$ and $y_0$ denote the initial position of the center of the MOT cloud, $\sigma _x$ and $\sigma _y$ are the Gaussian widths of the atomic distribution, and a is the acceleration. It was assumed that the widths of the cloud distribution in coordinate space do not change during the acceleration process, which is consistent with the assumption of the adiabatic acceleration without heating the atomic ensemble. The model function obtained in this way was used in a least squares curve fitting procedure in order to get the parameters of the mechanical momentum transfer, in particular, the value of the acceleration which determines the force acting on the atoms by the chirped laser pulses.

The purpose of the experiments was to study the effect of the multiphoton adiabatic momentum transfer as a function of the frequency sweep parameters, and to optimize these for maximum efficiency. Therefore, the acceleration of the MOT cloud was measured with different chirp speeds and pulse duration values, with varying offset of the frequency sweep. The frequency offset was controlled by varying the DC component of the drive current of the laser diode, that is, the region of the frequency modulation was shifted with respect to the atomic transition. At each setting of the interaction parameters, the images of the displaced MOT cloud were taken twice: with the forward propagating pulse train only, and with both the forward and backward propagating pulse sequences, in order to compare the mechanical effect of the single-side illumination with that of the overlapping retro-reflected pulse pairs. The picture of the initial position and spatial distribution of the MOT cloud without the modulated laser pulse train was also taken for reference. After evaluating the images of the displaced MOT clouds, the obtained acceleration values were displayed versus the frequency offset of the chirp.

The results of one measurement sequence can be seen in Fig. 5. The acceleration of the MOT cloud versus the detuning of the pulse central frequency from the atomic resonance (denoted by $\varDelta$) are shown for the single-side and two-sided illumination and the ratio of these two quantities is also depicted. Acceleration is measured in units of $\hbar k_L/T_{\mathrm{cycle}}$, i.e., in momentum change per laser pulse cycle, normalized by the photon momentum. The maximum pulse intensity was about $100\,{\mathrm {W/cm}}^{2}$ corresponding to the Rabi-frequency times pulse duration product $\varOmega _{\mathrm {R}}\times \tau =2\pi \times 8$. The pulse duration was about 7.7 ns, and the chirp rate about $-60$ MHz/ns. The maximum acceleration achieved by the counter-propagating pulses is $3.09\hbar k_L/T_{\mathrm{cycle}}$, near the symmetric frequency run with respect to the atomic resonance during the pulse. The maximum acceleration achieved by single-sided illumination is also at the same detuning value and is $1.36\hbar k_L/T_{\mathrm{cycle}}$, the ratio of the two quantities has a maximum of 2.3. The fact that the maximum momentum transfer for counter-propagating, overlapping pulses is over $3\hbar k_L$ per cycle indicates that multiphoton processes do take place during the interaction. The value does not equal $2n\hbar k_L$ however, so it cannot clearly be associated with an adiabatic process in itself. The maximum value for single-sided illumination is also higher than the single $\hbar k_L$ per cycle that can be attributed to single-photon absorption from a pulse followed by spontaneous emission. This is due to the pulse duration (7.7 ns) not being negligibly short compared to the spontaneous lifetime (26 ns). However, the fact that counter-propagating pulses are more than twice as effective is a firm indication that multiphoton processes are at work.

It should be noted that the fitting calculations were also attempted by including the possible broadening of the atomic cloud. However, inconsistent results scattering around zero and showing no reasonable value for this parameter were obtained. Probably the effect was too small to be resolved due to the long camera exposure time and thereby limited resolution of our measurement.

In the following, theoretical considerations and computer simulations are presented and compared to the experimental results shown here.

Fig. 5

Results of the multiphoton adiabatic acceleration experiment sequence performed with 7.7 ns pulse duration and $100\,{\mathrm {W/cm}}^{2}$ peak intensity of the chirped laser pulses. The acceleration of the MOT cloud (in units of $\hbar k_L/T_{\mathrm{cycle}}$) versus the detuning of the pulse central frequency from the atomic resonance is depicted for the single-side and two-sided illumination. The ratio of these two quantities is also drawn

3 The concept of computer simulations

As the experimental results in themselves do not demonstrate clearly the occurrence of multiphoton adiabatic passage processes, a detailed theoretical model of the experimental situation was derived and simulated on computer. There are several factors in the experiment that may make observation of these processes difficult. First, Rb has a complicated hyperfine structure, the lasers crossing the resonance frequency with some transitions, but not others. Second, we measure only the cumulative effect of a prolonged interaction of the atomic ensemble with the sequence of laser pulse pairs for a time much longer than the spontaneous lifetime. Third, because spontaneous decay may transfer the atomic state to the $F=2$ ground state that is out of the interaction range of the chirped pulses, a re-pumping beam is active during the experiment to prevent the accumulation of atoms in this non-interacting ground state, further complicating the situation.

3.1 Theoretical description

For the theoretical description of the experimental scenario we use the master equation for the interaction of the atoms with the laser fields which can be written in the compact operator form [42]:

$$\begin{aligned} \partial _t\hat{\rho }=-\frac{i}{\hbar }[\hat{H},\hat{\rho }] +\varGamma \frac{2J_e+1}{2J_g+1}\sum _q\mathscr { D } [ \hat{\sigma }_q ] \hat{\rho } , \end{aligned}$$

(2)

where $\hat{\rho }$ is the density operator, $\hat{H}=\hat{H}_{A}+\hat{H}_{AF}$, $\hat{H}_A$ is the atomic Hamiltonian, $\hat{H}_{AF}$ is the interaction Hamiltonian and $\varGamma$ is the spontaneous decay rate. The Lindblad superoperator $\mathscr {D}[c]$ for an operator c is defined as

$$\begin{aligned} \mathscr {D}[{c}]\hat{\rho }={c}\hat{\rho } {c}^{+} -\frac{1}{2}({c}^{+}{c}\hat{\rho }+\hat{\rho } {c}^{+}{c}) \end{aligned}$$

(3)

and $\hat{\sigma }_q$, are the atomic lowering operators for $\sigma ^+$, $\pi$ and $\sigma ^-$ polarizations

$$\begin{aligned} \hat{\sigma }_q=\sum _{F,m;F',m'}D_{F,m;F',m'}|F,m\rangle \langle F',m'| \end{aligned}$$

(4)

($m'=m-q$). The $|F,m\rangle$ and $|F',m'\rangle$ represent the ground and excited state hyperfine levels, respectively, and the coefficients $D_{F,m;F',m'}$ for $^{85}{\mathrm {Rb}}$ are tabulated in [43]. The atomic Hamiltonian operator with this notation is:

$$\begin{aligned} H_{A}=\sum _{F,m}\hbar \delta _{F}\left| F,m\right\rangle \left\langle F,m\right| +\sum _{F',m'}\hbar \delta _{F'}\left| F',m'\right\rangle \left\langle F',m'\right| . \end{aligned}$$

(5)

Here, $\hbar \delta _{F}$ and $\hbar \delta _{F'}$ represent the energy shifts relative to the ground and excited state line center and are defined using $\sum _{F}\delta _{F}\left( 2F+1\right) =0$, $\delta _{3}-\delta _{2}=2\pi *3035.7$ MHz for the ground and $\sum _{F'}\delta _{F'}\left( 2F'+1\right) =0$, $\delta _{4}-\delta _{3}=2\pi *120.6$ MHz, $\delta _{3}-\delta _{2}=2\pi *63.4$ MHz and $\delta _{2}-\delta _{1}=2\pi *39.4$ MHz for the excited states.

We describe the interaction with the classical laser field E in the dipole approximation, using the rotating wave approximation. The interaction Hamiltonian then assumes the following form:

$$\begin{aligned} H_{AF}=\frac{\hbar }{2}\sum _{F,m,F',m'}\left( \varOmega _{F,m,F',m'}\left| F',m'\right\rangle \left\langle F,m\right| +h.c.\right) \end{aligned}$$

(6)

Here, $\varOmega _{F,m,F',m'}$ is the Rabi frequency for the $\left| F,m\right\rangle \rightarrow \left| F',m'\right\rangle$ transition composed as $\varOmega _{F,m,F',m'}\!=\!D_{F,m,F',m'}\varOmega _{m-m'}$, where $\varOmega _{q}=-\frac{2}{\hbar }\left\langle J\right\| \hat{d}\left\| J'\right\rangle E_{q}$ with $\left\langle J\right\| \hat{d}\left\| J'\right\rangle$ being the reduced matrix element and $E_{q}$ is the positive frequency part of the q component of the field in a spherical basis. This formalism is capable of describing the time evolution of the atomic system under the action of any number of laser fields with decoherence due to spontaneous emission included. Additional coherence decay mechanisms (e.g., due to collisions) are negligible in our case.

The first part of the field used in our simulation is the pair of Gaussian pulses propagating along the z direction with linear polarization:

$$\begin{aligned} \varOmega ^{\pm }(t)=\frac{A^{\pm }}{2} \exp \left( {-\frac{(t-t_d^{\pm })^{2}}{2\tau ^{2}}}+{i\varphi ^\pm (t)}\right) . \end{aligned}$$

(7)

Here, $\varOmega ^{\pm }$ are the complex, slowly varying envelope functions for the field. The upper (lower) indices are for the pulse propagating in the positive (negative) z directions, $\tau$ is the pulse duration parameter, $t_d^+=0$, $t_d^-=\tau _d$ is the delay of the second pulse. The phases are taken to represent pulses with linear frequency chirping:

$$\begin{aligned} \varphi ^\pm =-\varDelta (t-t_d^\pm )-\frac{\beta }{2}(t-t_d^\pm )^2-\varphi _{0}^\pm \end{aligned}$$

(8)

where $\varDelta$ and $\beta$ are the detuning from the atomic resonance and chirp speed, respectively (the same for both pulses). One of the initial phases was assumed $\varphi _0^+=0$, while the other accounts for atoms that (due to a slightly different location along the z-axis) interact with the counter-propagating pulses having a different relative phase. In addition to the counter-propagating pulse pair, the CW radiation responsible for re-pumping from the $F=2$ ground state sublevel is also added as this field is not switched off during the interaction.

Once the time evolution of the atomic state has been calculated, the mechanical effect of the pulse pair on the atom was calculated via the quasi-classical force as in [25]

$$\begin{aligned} \hat{F}&=-\nabla \hat{H}_{AF} \nonumber \\&=-\frac{\hbar }{2}\sum _{\begin{array}{c} {F,m}\\ {F',m'} \end{array}}\left\{ |F,m\rangle \langle F',m'|\left( ik\varOmega _{F,m,F',m'}^{-*} - ik\varOmega _{F,m,F',m'}^{+*}\right) \right. \nonumber \\&\quad +\left. |F,m\rangle \langle F',m'|\left( ik\varOmega _{F,m,F',m'}^{+}-ik\varOmega _{F,m,F',m'}^{-} \right) \right\} , \end{aligned}$$

(9)

(The spatial derivatives of the slowly varying envelopes $\varOmega ^\pm (t)$ were neglected). The expectation value of the momentum transfer to the atom is thus given by

$$\begin{aligned} \langle \varDelta p\rangle =\int {\mathrm Tr}[\hat{\rho }\hat{F}]\mathrm{d}t. \end{aligned}$$

(10)

which still depends on the relative phase parameter $\varphi _0^-$. To calculate experimentally observed quantities, one must perform a scan in the range $\varphi _0^-\in [0,2\pi ]$ and average the results to take into account that atoms at slightly different locations experience a different relative phase between the two counter-propagating fields. Therefore, calculating the average $\overline{\langle \varDelta p\rangle }$ with respect to the $\varphi _0^-$ scan as well as the standard deviation $\sigma _{\varDelta p}$ gave us the overall acceleration of the atomic ensemble as well as the possible heating of the atomic cloud.

3.2 Signatures of multiphoton adiabatic passage

With certain pulse length, intensity, frequency chirp and time delay parameters, the counter-propagating laser pulse pair may drive multiphoton adiabatic passage, which shows up in the simulation as $\overline{\langle \varDelta p\rangle } = 2n\hbar k$ and $\sigma _{\varDelta p}=0$ simultaneously for an atomic ensemble initially in the ground state. This happens not only for two-level atoms, but also for the complicated level-scheme of $^{85}{\mathrm {Rb}}$. However, in this case they were found to occur only when the pulse bandwidth is considerably wider than that used in this experiment [25]. Furthermore, under the current experimental conditions, the interaction of a single pulse pair with an ensemble in the ground state cannot be observed, only the effect of a prolonged interaction with a duration much longer than the spontaneous lifetime. This is not necessarily a major problem because if the delay time between the two pulses of the counter-propagating pair is much smaller than the time between the pairs, the momentum transferred to the ensemble as well as the heating will be close to the ideal $\overline{\langle \varDelta p\rangle } = 2n\hbar k$ and $\sigma _{\varDelta p}=0$ values [44, 45]. Thus, the signature of multiphoton adiabatic passage happening can still show up as a ‘plateau’ in the curve of $\overline{\langle \varDelta p\rangle }$, coupled with a minimum in $\sigma _{\varDelta p}$ as pulse parameters are varied slightly.

4 Results of the simulations

4.1 The effect of a single pulse pair

To investigate whether we may observe the signatures of multiphoton adiabatic passage processes under the current experimental circumstances, we performed several numerical simulations to determine the behavior of the atoms during the interaction. First, we computed the interaction of an atomic ensemble with a single pulse pair using pulse parameters identical to those in the experiment (peak intensity $I_{\mathrm{peak}}=100\,{\mathrm {W/cm}}^{2}$, pulse duration $\tau =7.7\,{\mathrm {ns}}$ (intensity FWHM), chirp speed $\beta =-62\,{\mathrm {MHz/ns}}$ and the detuning $\triangle =-40\,{\mathrm {MHz}}$). We examined the average momentum transferred to the ensemble $\overline{\langle \varDelta p\rangle }$ as well as the heating of the ensemble $\sigma _{\varDelta p}$ as a function of the delay between the pulses $\tau _d$. The atoms were assumed to be in the $F=3$ ground state initially for this calculation. Figure 6 shows the results, clearly displaying peaks of increasing momentum transfer with the simultaneous drop in standard deviation in the vicinity of the peaks just as expected from previous theoretical calculations [25, 32]. The value of momentum transfer is closest to ideal in the case of the peak around 8.5 ns delay, where the maximum momentum transfer is 3.34 $\hbar k$, quite close to the ideal $4\hbar k$ level and the heating is also the lowest. The process is not perfect however, mostly due to the fact that the overall duration of the process (7.7 ns pulses with 8–9 ns delay) is the same order of magnitude as the lifetime of the excited state. The higher peaks which should correspond to $6\hbar k$, $8\hbar k$, etc. are even further from ideal, (the transferred momentum is much less) not only because of spontaneous emission, but also because the intensity is insufficient for perfect adiabatic passage.

Fig. 6

Momentum transferred by a single pulse pair to the atomic ensemble $\overline{\langle \varDelta p\rangle }$ and ensemble heating $\sigma _{\varDelta p}$ as a function of delay between pulses $\tau _d$

It is interesting to observe that the $2\hbar k$ plateau (non-overlapping pulse case) seems not to work at all even though it is this process that would require the smallest intensity. One reason for this is of course that with pulse durations over 7 ns and a delay exceeding 12 ns, spontaneous emission has a serious effect. Another important reason for this peculiarity is associated with the excited state hyperfine structure of $^{85}{\mathrm {Rb}}$ and the fact that the pulse duration and the full bandwidth are such that the pulse overlaps resonance with several excited state hyperfine sublevels sequentially. The first pulse, being chirped from blue to red becomes resonant with the $F=3\rightarrow F'=4$ hyperfine transition first and thus transfers the atomic population to $F'=4$. By the time it becomes resonant with the $F=3\rightarrow F'=3$ and $F=3\rightarrow F'=2$ transitions, the ground state is already empty. The second pulse, becoming resonant with the $F=3\rightarrow F'=4$ transition returns the atomic population to the $F=3$ ground state only temporarily. It subsequently becomes resonant with the $F=3\rightarrow F'=3$ and $F=3\rightarrow F'=2$ transitions and the atoms are excited again (in fact they are distributed between the two excited states $F'=3$ and $F'=2$). The momentum eventually transferred by the two pulses is not $2\hbar k$. Figure 7 shows the corresponding changes of the atomic state populations during the laser pulses. In order to illustrate the series of population transfers during the pulse sequence clearly, these populations were calculated without taking spontaneous emission into account.

Fig. 7

Populations of the hyperfine levels during the interaction with a pair of identical, non-overlapping, chirped laser pulses. The atom is transferred to the excited state $F'=4$ by the first pulse, but transferred eventually to a superposition of the $F'=2$, $F'=3$ hyperfine states by the second pulse. Spontaneous emission was ignored in this calculation. The dotted line shows the time dependence of the laser pulse amplitude

It is thus quite significant that in the overlapping pulse case the population transfer (and momentum transfer) works quite well for the $4\hbar k$ plateau despite the hyperfine-level structure. As an interesting test, we repeated the non-overlapping pulse calculation with the chirp of the second pulse reversed, i.e., going from red to blue. The $2\hbar k$ momentum transfer and the return of the atoms to the $F=3$ ground state is achieved in this case because the second pulse becomes resonant with the $F=3\rightarrow F'=3$ and $F=3\rightarrow F'=2$ transitions when the ground state is still empty. Naturally, such a reversal cannot be achieved in the experiment with the pulses simply being retro-reflected from a mirror. Furthermore, such an approach is not convenient because multiphoton adiabatic passage cannot be induced with two pulses of opposite chirp direction.

Finally, Fig. 8 shows the momentum transfer by a pair of overlapping pulses and by a single pulse (no retro-reflected, counter-propagating pulse) as a function of the central detuning with a delay $\tau _d=3$ ns, the same as used in the experiment. It can be seen that the momentum transferred by a single pulse in the adiabatic interaction regime is around $1 \hbar k$, the value slightly exceeding it is due to the duration of the pulse being not much smaller than the spontaneous lifetime. At the same time, overlapping pulses deliver much more momentum per pulse pair. However, the experimental delay of $\tau _d=3$ ns is not at a momentum transfer peak as can be seen in Fig. 6, which also shows that there is a considerable heating at this delay as well.

Fig. 8

Momentum transfer by a pair of overlapping laser pulses (solid line) and by a single pulse (dashed line) to an atomic ensemble, as a function of the central detuning of the chirped pulse. The laser pulse parameters are the same as for the calculations shown in Fig. 6, the delay is $\tau _d=3$ ns. The atoms are in the $F=3$ ground state initially

4.2 The effect of a sequence of pulse pairs

Clearly, the effect of a single pulse pair cannot be observed in the experiment because the sequence of laser pulses was gated to allow about 5000 pulse pairs to interact with the atomic cloud. Therefore, what we can observe is only the cumulative effect of the 5000 laser pulse pairs, the effect of a single pair has to be inferred from this observation. However, to calculate the interaction with 5000 pulse pairs for comparison of theory and experiment is not feasible for lack of sufficient computing power.

It has been shown that for two-level atoms the atomic populations reach a stationary state (or, more precisely a limit cycle) under the effect of the periodic driving of repeated laser pulse pairs [44, 45], provided the interaction lasts much longer than the excited state lifetime. The time dependence of the atomic populations will be exactly the same during each laser pulse cycle. The overall momentum gain delivered by a pulse pair, as well as the overall diffusion in momentum space (heating) will thus also converge to a constant, ‘stationary state’ value. We are dealing with a much more complicated level scheme in this case, but it is not unreasonable to expect a similar behavior, i.e., convergence to a stationary state for the momentum delivered per pulse pair. If so, it is meaningful to compare the stationary state momentum transfer to the average momentum transfer of the 5000 pulse pairs of the experiment.

Further complications arise in the present case because a re-pumping field is necessary which provides optical pumping from the $F=2$ ground state and the fact that the gating of the pulses yields gradually increasing pulse amplitudes for the first 500–600 pulse pairs. Another property of the experiment was that while the laser beams of the MOT were turned off to prevent trapping forces to interfere with acceleration provided by the pulses, the magnetic fields were still present. This means that hyperfine levels split and resonance frequencies are shifted due to the Zeeman effect as the atoms move out of the trap center. Finally, as the atomic cloud accelerates, the central frequency of the laser pulses propagating in opposite directions Doppler shifts in an opposite sense, complicating the interaction even more. Unfortunately, it is not possible to take into account all of these effects in the simulation exactly.

To calculate the long-term effect of the counter-propagating pulses on the atomic ensemble, we calculated the interaction of 30 laser pulse pairs with the atoms and computed the evolution of the momentum gain, as well as the heating effect on the ensemble from cycle to cycle. We repeated the calculations with the two pulses of a pair Doppler shifted in opposite sense by the same amount using several values of Doppler shift. This helps us evaluate the effect of frequency shifts introduced by the atoms accelerating during the interaction. The re-pumping field was on during all these calculations, preventing the buildup of atomic population in the off-resonance ground state just as it was during the experiment. We observed that most of the time, $\overline{\langle \varDelta p\rangle }$ did converge to a stationary value as expected, but in some cases, the momentum change per pulse itself converged to a limit cycle behavior with a period of a few pulse pair cycles. Depending on the value of the detuning and the Doppler shift, we observed periods of 2, 5 and 10 pulse pairs. (The calculation was continued for longer than 30 pulse pairs in these cases to observe the convergence of the calculation to these limit cycles.) When the cumulative effect of a large number of laser pulse pairs is considered, we must average the momentum gain over these limit cycles in addition to averaging for the relative phase $\varphi ^-$. This is the true long-time average for the momentum transfer and heating (momentum space diffusion) which can be considered for comparison with the experimental data.

5 Comparison with experimental data and discussion

To obtain theoretical values that can be compared with the measured values, we calculated the long-time average of the momentum transfer and ensemble heating for parameters corresponding to the experiment: $I_{\mathrm{peak}}=100\,{\mathrm {W/cm}}^{2}$, $\tau =7.7\,{\mathrm {ns}}$, $\beta =-62\,{\mathrm {MHz/ns}}$, $\tau _d=3\,\mathrm{\mathrm {ns}}$ and for the power in the re-pumping beam, $P_{p}=7.5\,{\mathrm {mW/cm}}^{2}$. The detuning was scanned between $-1$ GHz to $+0.55$ GHz to obtain data comparable with the observations. To check the sensitivity of the results with respect to the acceleration of the atoms, we repeated the calculation for several values of Doppler detuning. The Doppler values were selected to correspond to reasonable values after an interaction with a few hundred pulse pairs, as seen by comparing with the single recoil-event Doppler detuning value $D_{vr}=7.7194\,{\mathrm {kHz}}$ [42].

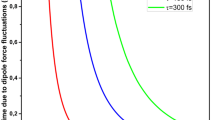
The stationary state of the average momentum transferred to the atoms by a pair of counter-propagating laser pulses can be seen in Fig. 9 for several values of the Doppler detuning. The experimental value is also plotted on each of the figures for reference. It is immediately visible, that for some values of the Doppler detuning, the transferred momentum curve follows quite well the experimental data, for others it is well above or below it. There is also a slight shift along the detuning for the curves which agree most with the experiment.

Fig. 9

Long-time average of the momentum transferred to the atomic ensemble (solid blue line) and the heating of the ensemble (dashed red line) as a function of the detuning for several values of the Doppler detuning. The experimental value for the momentum transfer per cycle is drawn on each subfigure with a dotted green line for reference

Obviously, none of the plotted curves can be directly compared to the experimental data on its own. During the prolonged interaction with the laser pulses, the atoms will be accelerated and the Doppler detuning changes as the atomic velocity increases, so the momentum transfer per pulse pair also changes in time as shown in Fig. 9. The experimentally measured curve is therefore some average over the displayed theoretical curves. Indeed, calculating $\overline{\langle \varDelta p\rangle }$ for a single detuning, but a detailed set of Doppler values we may observe, that the atoms experience a series of transitions across momentum transfer maxima and minima as they are accelerated (see Fig. 10). The curves resemble the momentum transfer and heating curves plotted as a function of $\tau _d$ of Fig. 6 and are in fact very closely related. Because the chirp is close to linear near the pulse maximum, a slight frequency shift means that the forward propagating pulse will become resonant with the atomic transitions a bit sooner, while the backward propagating pulse a bit later. Thus, Doppler shifting the forward and backward propagating pulses in an opposite sense effectively increases the delay parameter between the pulses.

Fig. 10

Momentum transferred to the ensemble by a pair of overlapping pulses and the heating of the ensemble for $\varDelta =0$ GHz as a function of the Doppler detuning. a The effect of the first pulse pair and b the long-time average after reaching the stationary state. $\tau _d =3$ ns, other pulse parameters are the same as for the previous figures

It can also be seen by comparing the subfigures of Fig. 9, that the trend that when $\overline{\langle \varDelta p\rangle }$ is large, the heating tends to be smaller is true for any value of $\varDelta$, not only $\varDelta =0$. This, together with the fact that the long-time average of the momentum transfer is $\overline{\langle \varDelta p\rangle }> 2\hbar k_L$, clearly indicates that multiphoton adiabatic processes, though imperfectly realized, occur during the long-term evolution of the atomic translational states. Because of the prolonged interaction, several multiphoton order processes are probably active during the acceleration one after the other. The coherent acceleration due to a single multiphoton plateau is limited in time by the changing effective delay between the pulses due to a changing Doppler shift and the atomic ensemble experiences heating during the transition between processes with various multiphoton orders. This certainly sets a limit on the applicability of the method.

Finally, we note that in our experiment, the average force that the atoms experience will be dependent slowly on time also because when the atoms leave the trap center, an increasing magnetic field shifts the resonance frequencies by an increasing amount. This additional complexity was not taken into account in the calculations.

6 Summary and conclusion

To summarize, we have studied the interaction of counter-propagating, frequency-chirped laser pulses that overlap each other with a cloud of Rb atoms initially captured in a magneto-optical trap. We measured the average acceleration of the atomic cloud due to prolonged interaction with a large number of laser pulse pairs. We performed numerical simulations of the interaction that included the complex multilevel structure of the $D_2$ line of rubidium, spontaneous relaxation processes and the various laser fields active during the interaction. The overall momentum transferred to the atomic ensemble cannot be calculated exactly in this fairly complex experimental situation, so a precise quantitative comparison between experimental data and simulation results is not possible. Nevertheless, the good qualitative correspondence between the two suggests that the simulations can be used to interpret the interaction and the observed acceleration of the atomic cloud.

Theory and experiment suggest that the atomic cloud is accelerated due to multiphoton adiabatic transitions induced by the overlapping pulses. The fact that the overall average momentum transfer per pulse pair is greater in the experiment than $2\hbar k$ is firm evidence for this. We showed that the acceleration process can persist for times much greater than the spontaneous lifetime. At the same time, it is clear that the combined effects of long-time interaction with spontaneous emission, population loss to and re-pumping process from the $F=2$ hyperfine-level, spatially dependent magnetic field and time-dependent Doppler detuning all work together to break down a clean adiabatic process in our case.

Nevertheless, we proved that multiphoton adiabatic passage induced by counter-propagating, overlapping frequency-chirped pulses is an effective tool for the acceleration of an atomic ensemble. The overlapping pulse case is better than the sequence of counter-propagating, non-overlapping pulses for several reasons. First, the interaction time is much shorter for a single pair (much less time for spontaneous emission), so the coherence of the interaction is maintained more easily. Second, the momentum transferred by a single pulse pair is $2n\hbar k$, some integer multiple of the $2\hbar k$ momentum transferred by the adiabatic interaction with a pair of non-overlapping pulses. The order of the process depends on the interaction parameters (pulse duration, pulse delay, chirp speed, pulse peak intensity). Third, multiphoton adiabatic transitions generated by overlapping pulses are more robust when the bandwidth of the pulses is wide enough to encompass multiple excited state hyperfine sublevels, but not wide enough such that the transform limited bandwidth is higher than sublevel separation. In this setting, separated pulses transfer atoms to the wrong final state if the direction of the chirp for pulses is the same. Overlapping pulses are not only several times more effective in this case, but they are the only possible tool that can be used. Finally, we also showed that the increasing Doppler detuning of the pulse frequencies when the atoms accelerate effectively changes the delay parameter between the pulses of an overlapping pair. This limits the time for which a single multiphoton order interaction can be effective. For prolonged interaction, several different multiphoton orders may be traversed with transition periods between them where the atomic ensemble is heated.