First observation of rotational bands in the nucleus $^{231}$U

Abstract

This work reports the first rotational bands observed in the neutron-deficient nucleus $^{231}$U. Excited states were populated in the $^{232}$Th($\alpha$,5n) reaction at a beam energy of 52 MeV. Coincident decay $\gamma$-rays were measured with the high-purity germanium detectors of the afrodite spectrometer array, in conjunction with a recoil detector to discriminate against the fission background. The bands are interpreted as the ground-state band $\nu [633]5/2^{+}$, yrast band $\nu [752]5/2^{-}$, and an excited band $\nu [631]3/2^{+}$. Configuration assignments are supported by Cranked Shell Model and B(M1)/B(E2) calculations. The excitation energy of the $\nu [752]5/2^{-}$ bandhead is suggested to be 113.0 keV.

1 Introduction

Uranium-233 is currently the lightest odd uranium (Z=92) isotope known to support rotational bands [1]. Our present knowledge of the next lightest odd uranium isotope, $^{231}$U$_{139}$, is limited to six excited states studied in $^{231}$Np $\beta$-decay and $^{235}$Pu $\alpha$-decay, and its ground-state configuration is not firmly established [2]. In this work we report the first rotational bands observed in $^{231}$U.

The light actinides are of interest because they are predicted to exhibit axial reflection-asymmetric [3] and tetrahedral [4] shapes. We performed a series of three experiments involving $^{232}$Th($\alpha$,xn) reactions as part of a campaign to search for these phenomena in the $A \simeq 230$ mass region. The experiments employed beams of 42, 52 and 61 MeV to produce an extended data set. The results of the 42- and 61-MeV data have been published [5]. The present work is based mainly on the 52-MeV data, which confirms the existence of several new rotational bands, some of which had also been observed in the 61-MeV data. We identify the new bands as belonging to $^{231}$U.

Fig. 1

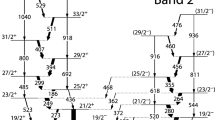
New rotational bands in $^{231}$U. States observed in our data appear as bold horizontal lines, and tentative levels as dashed lines, with the lowest levels extrapolated. The arrow widths reflect the $\gamma$-ray intensities. Tentative spin-parity values and tentative transitions appear in parentheses. Crossover $\Delta I=1$ transitions which were not observed, but inferred from intensity balances, are enclosed in square brackets. The excitation energy of Band 3 is chosen to be consistent with CSM predictions. The $\gamma$-rays energies are in keV

Fig. 2

The figure shows relevant parts of the yrast bands of the neighbouring nuclei $^{230}$U, $^{232}$U and $^{233}$U [5, 18, 19]. States observed in our 52-MeV data appear as bold horizontal lines, while previously known levels which are absent from the data are shown as narrow lines

The experimental details are described in Sect. 2. The evidence for placing the bands in $^{231}$U, Cranked Shell Model (CSM) calculations supporting the configuration assignments, and the level scheme are discussed in Sect. 3, followed by a brief discussion and summary in Sects. 4 and 5.

2 Experiment

Excited states in $^{231}_{92}$U were populated via the $^{232}$Th($\alpha$,5n)$^{231}$U reaction at a beam energy of 52 MeV. The $^{232}_{90}$Th target foil, of thickness 127(5) $\mu$g/cm$^{2}$, was supported by a 20 $\mu$g/cm$^{2}$ carbon layer facing the on-coming beam. The thin target allowed recoiling residual nuclei to escape and interact with a recoil detector located 145 mm downstream. The K=200 iThemba LABS Separated Sector Cyclotron provided the pulsed beam, with beam bursts 307 ns apart. The dominant residual nuclei were $^{230}$U ($\sim 5\%$), $^{231}$U ($\sim 28\%$), $^{232}$U ($\sim 34\%$), $^{234}$U ($\sim 11\%$), and $^{229,231,233}$Pa ($\sim 21\%$), where the figures in parentheses denote approximate percentages of the total production yield, excluding fission. Trace amounts of $^{233}$U ($< 2\%$) were also present in the data.

Coincident $\gamma$-rays were measured with the afrodite spectrometer array comprising nine suppressed Clovers and three unsuppressed leps detectors. A significant difficulty in the spectroscopy of light actinide nuclei is the intense competiton from fission. The array was therefore operated in coincidence with the recoil detector, described in [5], in order to discriminate between $\gamma$-rays emitted by residual nuclei and those emitted by the fission background. The recoil detector allows one to measure the time-of-flight of nuclei from the target to the detector. When reactions ensue following a beam pulse, the recoiling nuclei evaporate neutrons and undergo multiple scattering within the target, emerging in a roughly cone-shaped burst. The reaction products then encounter a mylar foil in the recoil detector, from which they eject electrons. These are accelerated and then guided by a weak magnetic field in a semi-circular arc onto a micro-channel plate (MCP) immediately above the foil, producing the MCP signal, with the time measured relative to the pulsed beam. It is thus possible to select $\gamma$-rays associated with the slower-moving residual nuclei (as opposed to the faster fission fragments and scattered beam) during the off-line analysis by setting a time gate on the data. The electronics are configured to accept recoils during a 200 ns time window encompassing the expected time-of-flight.

The master event trigger demanded a coincidence between the recoil detector and any one of the Clovers. We found that the $\gamma$-recoil trigger condition suppressed the event rate, compared with the raw $\gamma$-$\gamma$ event rate, by $\sim 99\%$. During the offline data analysis the data were sorted into a two-dimensional MCP-energy vs. time-of-flight spectrum. This intermediate energy-time matrix was then used to select coincident $\gamma$-rays associated with the residual nuclei by imposing a suitable 2-dimensional gate, and the events selected in this way were placed in a symmetric $\gamma$-$\gamma$ matrix, containing $\sim 10^{7}$ events, for subsequent analysis using Radware [6].

3 Results

The three new structures which we will associate with $^{231}$U, Bands 1, 2 and 3, are shown in Fig. 1. The bands were constructed according to $\gamma$-$\gamma$ coincidence relationships and intensities. In addition, the low-spin parts of previously known yrast bands in the neighbouring uranium isotopes $^{230}$U, $^{232}$U and $^{233}$U, which are useful for comparison, are shown in Fig. 2.

In this section we present experimental evidence for placing the new bands in $^{231}$U, followed by a discussion of the CSM calculations which are used as a guide for the construction of the level scheme. The electromagnetic properties of the proposed configuration assignments of the bands are analysed to reproduce the observed spectra.

3.1 Identification of new bands with $^{231}$U

All rotational bands in our data could be positively identified with proctactinium or uranium, based on coincidences between the in-band transitions and the distinct protactinium or uranium x-rays. Protactinium isotopes $^{229}$Pa and $^{233}$Pa were among the reaction products, and are not discussed in this work. The uranium isotopes $^{230}$U, $^{231}$U and $^{232}$U were the dominant reaction products in the 52-MeV data.

Fig. 3

Coincidence spectrum for Band 1, gated on the 113-keV transition near the bottom of the band. The 98.4 and 94.7-keV uranium K$\alpha$ X-rays are clearly visible. The gating transition is labelled with an asterisk

Fig. 4

These spectra contrast the different $\gamma$-ray intensity patterns in the $^{231}$U and $^{232}$U yrast bands. Asterisks denote energy gates. Note the 98.4 and 94.7-keV uranium X-rays. a Coincidence spectrum gated on the 304-keV transition in $^{231}$U. The simulated spectrum is shown in red, see Sect. 3.3 for details. b Spectrum gated on the analogous 306-keV transition in $^{232}$U

Fig. 5

Spectra for Band 2, showing the 98.4 and 94.7-keV uranium X-rays. The energy gates are labelled with asterisks. a Summed coincidence spectra gated on 178, 226, 270 and 311 keV. b Summed coincidence spectra gated on the 202, 249 and 292 keV. Known contaminants from the $^{229}$Pa yrast band are labelled c

Fig. 6

Spectra for Band 3, showing the 98.4 and 94.7-keV uranium X-rays. The energy gates are labelled with asterisks. Each spectrum has a prominent contaminant peak from protactinium, labelled c. a Coincidence spectrum gated on the 210-keV transition of the observed decay sequence. b Summed coincidence spectra gated at 188, 231, 271 and 308 keV suggest a tentative signature partner in Band 3. See text for details

Spectra supporting the existence of the new bands are shown in Figs. 3, 4, 5 and 6. The bands can all be assigned to uranium based on the prominent display of uranium x-rays at 94.7 and 98.4 keV in the spectra. Band 1 is the most strongly populated. Two $\gamma$-ray sequences of this band are revealed by the gate on the 113-keV transition in Fig. 3. The stronger sequence has transition energies similar to the ground-state band of $^{232}$U, but is distinct from $^{232}$U, as shown in Fig. 4, where a gate on the 304-keV transition of Band 1 is compared with the gate on the 306-keV transition of $^{232}$U. The spectra revealing the transition sequences of Bands 2 and 3 were formed by summing multiple gates on the bands, and are shown in Figs. 5 and 6.

Fig. 7

Theoretical uranium production cross sections exceeding 1 mb, as a function of beam energy, calculated using the code pace4. The fission cross section is predicted to be $\sim 2$ b

To assign these new bands to $^{231}$U, we constructed experimental relative excitation functions using the extended 42–52-61-MeV data set. In fusion-evaporation reactions, the 4n, 5n and 6n reaction-channel cross sections follow a specific pattern that depends on the beam energy. As an example, the pace4 [7] calculations for the 4n, 5n and 6n exit channels for the $\alpha$+$^{232}$Th reaction are shown in Fig. 7.

The yield of band i in isotope 23n of uranium is given by

$$\begin{aligned} {N}_{^{23n}{U}_{i}}(E) = {b}_{i}{\sigma }_{^{23n}{U}}(E){Q(E)}{\varepsilon }(E)x(E) \end{aligned}$$

(1)

where $\sigma _{^{23n}{U}}$ is the reaction cross-section and ${b}_{i}$ represents the branch into band i. Since the integrated charge Q(E), target thicknesses x(E) and recoil detector efficiencies ${\varepsilon }(E)$ were not measured accurately across the data set, we eliminated the uncertain quantities by forming the ratio

$$\begin{aligned} \frac{{N}_{^{23n}{U}_{i}}(E)}{{N}_{^{231}{U}_{A}}(E)} = \frac{{b}_{i}{\sigma }_{^{23n}{U}}(E)}{{b}_{A}{\sigma }_{^{231}{U}}(E)} \end{aligned}$$

(2)

which is the yield of individual bands relative to Band 1. By definition this quantity is unity for Band 1, and should be approximately constant for other bands assigned to $^{231}$U, while according to the PACE calculations it should be a falling function of energy for $^{232}$U, and a rising function for $^{230}$U. Although there were insufficient statistics to form this ratio for Bands 2 and 3 at 42 MeV, this pattern is otherwise observed in the ratios plotted in Fig. 8, and imply that Bands 1, 2 and 3 can be assigned to $^{231}$U.

We note here that the observation of $^{232}$U in our data at 52 MeV is not predicted by the calculations and implies significant yield from alternative reaction mechanisms at the higher energies. Hogan et al. [8] highlight the importance in $\alpha$-particle reactions on fissile targets of $\alpha$-particle fragmentation and interactions with single nucleons.

3.2 The $^{231}$U level scheme

Although there were insufficient statistics to determine the multipolarity of the $\gamma$-rays through directional correlations of oriented states (DCO) or $\gamma$-ray polarization measurements, the energy patterns are generally consistent with in-band stretched E2 transitions of a rotational nature. Most of the $\gamma$-ray transitions in uranium nuclei suffer strong competition from conversion electrons, particularly for M1 transitions and the lower-energy E2 transitions near the bottom of the bands. Consequently, many E2 and M1 transitions are expected to be unobserved, precluding the measurement of absolute excitation energies.

Therefore to construct the level scheme, and make tentative spin assignments, we are guided by the Woods-Saxon model calculations of Bengtsson et al. [9]. Their predictions for $^{232}$U place three Nilsson orbitals close to the Fermi surface, arising from the spherical shell model $j_{15/2}$, and (mixed) $i_{11/2}$ and $g_{9/2}$ orbitals. These are the Nilsson orbitals labelled as $[752]5/2^{-}$, $[633]5/2^{+}$ and $[631]3/2^{+}$.

Furthermore, to understand the evolution of bands based on these orbitals with increasing rotational frequency, we performed Cranked Shell Model (CSM) [10] calculations for $^{231}$U, using the Woods-Saxon CSM [11] with deformation parameters $\beta _{2}$=0.208 and $\beta _{4}$=0.096 as used for $^{232}$U by [9]. A value of 0.7 MeV, derived from odd-even mass differences, and scaled down by 0.85 to mimic pairing blocking, was used for the pairing gap, $\Delta$. The theoretical quasineutron Routhians are shown in Fig. 9. The labelling convention for the Routhians is summarized in Table 1, along with the predicted alignments. The negative-parity $j_{15/2}$ $[752]5/2^{-}$ Routhians (E and F) lie closest to the Fermi surface and are predicted to be yrast, with the the favoured branch (E) having an alignment of 3.1 $\hbar$. A signature splitting of around 60 keV is expected between the partners at $\hbar \omega = 150$ keV.

The next two bands (associated with the A, B and C, D Routhians, respectively) are the positive parity bands based on the (mixed) $[633]5/2^{+}$ and $[631]3/2^{+}$ Nilsson orbitals. Both Woods-Saxon and Nilsson model calculations of Bengtsson et al. [9] place the $\Omega = 5/2$ orbital as the lower of the two. They are predicted to have small signature splitting, less than 10 keV in magnitude at $\hbar \omega = 150$ keV, and both should have less alignment, of around 1.5 $\hbar$.

With this information we turn to the observed bands to construct the level scheme. The yrast band, Band 1, must be identified with the $j_{15/2}$ configurations E and F. Table 2 lists the transition energies, normalized relative intensities, and tentative spin-parity assignments for the bands. In the 113-keV gate (Fig. 3) we observed two lines (157.1 and 122.4 keV) connecting the signature partners of Band 1. These $\Delta I\,=\,1$ crossover transitions, together with the 252.5 and 217.8-keV in-band transitions, form a unique closed summation loop which fixes the energy of the unfavoured signature relative to the yrast band, and implies a signature splitting of $\simeq 50$ keV, in good agreement with the predicted splitting of 60 keV of the $j_{15/2}$ band. The tentative choice of spins for Band 1, shown on the level scheme, brings the aligned angular momenta of Band 1 in reasonable agreement with the CSM prediction. In Fig. 10a the aligned angular momenta of the bands in $^{231}$U, with our tentative spins, are compared to that of the experimental ground-state band of $^{232}$U shown in Fig. 2. The favoured signature of Band 1 has 3.5 $\hbar$ relative to $^{232}$U, compared to a calculated 3.1 $\hbar$, see Table 1.

Fig. 8

Measured yields of bands in uranium isotopes relative to the yield of Band 1, as defined in Eq. 2, as a function of beam energy, in units of MeV

Fig. 9

CSM-predicted quasineutron Routhians for $^{231}$U, see the text for details, and Table 1 for the labelling convention. Solid lines denote $(\pi ,\alpha ) = (+,+1/2)$, dotted $(+,-1/2)$, dot-dash $(-,+1/2)$ and dash $(-,-1/2)$

Fig. 10

a Measured alignments for bands in $^{231}$U. The $^{232}$U yrast band serves as a reference, shown as a solid line. b Measured Routhians for the bands in $^{231}$U. The excitation energy of Band 3 was chosen to be consistent with CSM predictions. In both panels, open symbols denote the $\alpha = +1/2$ signature and closed symbols $\alpha = -1/2$. The Harris parameters are $J_{0}=62$ $\hbar ^{2}$MeV$^{-1}$ and $J_{1}=523$ $\hbar ^{4}$MeV$^{-3}$

These spin assignments imply that we have not observed the head of Band 1. The levels fed by the 153 and 171-keV transitions have $I^{\pi }$ of $(13/2^-)$ and $(15/2^-)$, respectively, and not 5/2$^-$ and 7/2$^{-}$, as implied by our $[752]5/2^{-}$ assignment.

Considering the observed $\gamma$-ray energies and the proposed tentative spins, we extrapolated the bands to lower spins, see the dashed-line levels in Fig. 1. Stretched E2 transitions of $\sim 104$ and $\sim 58$ keV are expected at the bottom the positive signature sequence, and $\sim 124$ and $\sim 77$ keV at the bottom the negative signature partner. However we did not observe such transitions, or any with similar energies. We note that the low-spin portion of the $[752]5/2^{-}$ band in the isotone $^{229}$Th deviates from the expected $I(I+1)$ pattern due to Coriolis mixing. The low-spin portion of this band is compressed, with a stretched E2 transition of only 27 keV feeding the bandhead [12]. Whether Band 1 exhibits similar compression is an open question. In any case, near the bandhead, low-energy magnetic transitions and associated conversion electrons should dominate.

The 113-keV $\gamma$-ray is in coincidence with both signature partners, as shown in Fig. 3, and is thus on the decay pathway of both partners. However, the intensity of the 113-keV transition is a noteworthy exception to the E2 pattern. In Fig. 4, it appears much stronger in the gate on the 304-keV transition of Band 1, than the 109-keV (E2) transition, visible in the gate on the 306-keV transition of the yrast band of $^{232}$U. This strongly suggests that the 113-keV transition has E1 character (with total internal conversion electron coefficient [14], $\alpha _T = 0.09$) rather than E2 character ($\alpha _T = 7.6$) or M1 character ($\alpha _T = 3.3$). To establish an experimental conversion coefficient from the data, with a quantitative analysis of intensity balances, requires knowledge of any dipole transitions linking the signature partners. This is explored further in section 3.3; here we tentatively assume the 113-keV transition is an out-of-band transition, such as the $5/2^- \rightarrow 5/2^+$ decay from the $[752]5/2^{-}$ bandhead to the head of the $[633]5/2^{+}$ band, as the latter band is predicted to be the lower of the $\Omega = 3/2^+$ and $5/2^+$ bands in the CSM calculations (Fig. 9). This would imply that the $[633]5/2^{+}$ band is the ground-state band. Alternatively the 113-keV $\gamma$-ray may be a $7/2^- \rightarrow 5/2^+$ transition. We note that the depopulation of the $[752]5/2^{-}$ band in the N=139 isotone $^{229}$Th is much more complex [12].

As Band 2 is populated more strongly than Band 3, it should lie lower in energy, and it is thus tentatively assigned to the $[633]5/2^{+}$ configuration. According to the CSM calculations shown in Fig. 9, the $[633]5/2^{+}$ band should have very little signature splitting. Unfortunately, the partners of Band 2 could not be linked by any $\gamma$-ray transitions, so there is no direct measure of their splitting. However, there is indirect evidence that this is indeed the case. In an odd-nucleus, in bands with good angular momentum projection $\Omega$, the $\Delta I = 2$, E2 $\gamma$-ray transition energies can be written as

$$\begin{aligned} E_{{\gamma }_{E2}}(I) = A \left[ (4I-2)+2a(-1)^{I+\frac{1}{2}}{\delta }_{\Omega ,1/2} \right] \end{aligned}$$

(3)

where a is the decoupling parameter, which gives rise to signature splitting both in the pure band, where $\Omega =1/2$, and in bands where the Coriolis interaction mixes in substantial components of the $\Omega =1/2$ orbital [13]. The average of the transition energies from states of higher and lower spin is

$$\begin{aligned}{} & {} 1/2 \left[ E_{{\gamma }_{E2}}(I-1) + E_{{\gamma }_{E2}}(I+1) \right] \nonumber \\{} & {} \quad = A\left[ (4I-2)-2a(-1)^{I+\frac{1}{2}}{\delta }_{\Omega ,1/2} \right] \end{aligned}$$

(4)

from which it follows that only in bands with little splitting, where the a-term is negligible, can Eq. 3 be equated to Eqn. 4, to give $E_{{\gamma }_{E2}}(I) = 1/2\left[ E_{{\gamma }_{E2}}(I-1) + E_{{\gamma }_{E2}}(I+1)\right]$. This condition is fulfilled by the partners of Band 2, with the appropriate choice of relative spins, and implies small signature splitting, as shown in Figs. 1 and 10b.

As with Band 1, the spins have been chosen to give an alignment consistent with the CSM calculation, with $\simeq 2 \hbar$ more alignment than the $^{232}$U reference. With these spin assignments, several of the transitions have very similar energies to their analogues in the $[633]5/2^{+}$ ground-state band of the nearest odd neighbour $^{233}$U, see Fig. 2. For example the 202.4-keV transition which depopulates the $(19/2^{-})$ level of Band 2 may be compared with the 203-keV transition which depopulates the $(19/2^{-})$ level of $^{233}$U. The spin assignments imply the existence to unobserved transitions near the head of the band as shown in Fig. 1. A low-spin extrapolation of the band sequences suggests that $\sim 130$-keV and $\sim 83$-keV $\gamma$-rays may depopulate the $(13/2^{+})$ and $(9/2^{+})$ levels, respectively, and $\sim 104$ keV the $(11/2^{+})$ level. However, we did not observe stretched E2 decays with these or similar energies. The excitation energy of the $\alpha =-1/2$ sequence is tentative, and was chosen to be consistent with zero signature splitting at low spins.

Table 1 Labels of the theoretical, quasineutron Routhians for $^{231}$U closest to the Fermi level. The predicted alignments are also given

Table 2 Measured $\gamma$-ray energies ($E_{\gamma }$) and $\gamma$-ray intensities ($T_{\gamma }$) normalized relative to the 217.8-keV transition in Band 1, which is assigned a value of 100. Tentative $\Delta I=1$ crossover transitions which were inferred from intensity balances, but not observed, are presented in square brackets. For such transitions, $T_{\gamma }$ was deduced from the calculated B(M1)/B(E2) ratios described in the text. The spin-parity ($I^{\pi }$) values are tentative and therefore appear in parentheses. Uncertainties in $\gamma$-ray energies are $\sim 0.2$ keV

Table 3 Intrinsic g-factors used for different quasiparticle orbitals, taken from reference [9], and the quantity $\left( g_{K} - g_{R} \right) ^{2} K^{2}$. The collective g-factor is $g_{R} = 0.26$. See the text for details

Table 4 Theoretical B(M1)/B(E2) and extracted branching ratios, $\lambda$, for the $[752]5/2^{-}$ band. It was assumed that $\delta =0$, and $Q_{0}=9.4$ eb [15]. The right hand column contains the ratio R, defined in Eq. 5. R is the ratio of the E2 $\gamma$-ray intensity depopulating a level to the intensity “lost” to competition by the $\Delta I$=1 crossover transition and electron conversion, and it decreases down the band. See text for details

Table 5 Nilsson configurations of the three lowest one-quasineutron states in the odd nuclei adjacent to $^{231}$U$_{139}$, followed by the excitation energy in parentheses, in units of keV. The excitation energy of the $\nu [752]5/2^{-}$ state in $^{231}$U is tentative. The other data are from [17]

In Table 3, we list values of $\left( g_{K} - g_{R} \right) ^{2} K^2$. The $[633]5/2^{+}$ assignment to Band 1 can be ruled out due to its very low value of $\left( g_{K} - g_{R} \right) ^{2} K^2 = 0.01$, which is two orders of magnitude lower than that of the $[752]5/2^{-}$ band. Crossover dipole transitions were not observed in Bands 1 and 2, but this is not surprising considering the smaller values of $\left( g_{K} - g_{R} \right) ^{2} K^2$ expected for the $[633]5/2^{+}$ and $[631]3/2^{+}$ bands, and the lower statistics.

This leaves the band populated the weakest, Band 3, as likely to be the band built on the $[631]3/2^{+}$ orbital. Initially, only the $\alpha = -1/2$ sequence was found, but the CSM predicts that the $[631]3/2^{+}$ band comprises a pair of signature partners with little splitting. A search was therefore made for the partner by gating on the intermediate energies of the observed transitions. The resulting spectrum, formed by summing gates on the 188, 231, 271 and 308-keV lines, and shown in Fig. 6, is of poor quality, but reveals a tentative signature partner. Band 3 could not be linked to the other structures.

3.3 Electromagnetic properties of the bands

A subtle effect is visible in Fig. 4. The gate on the 304-keV transition of the favoured signature of Band 1, in Fig. 4a, shows a decrease in intensity of successive transitions down the band. The 218-keV peak is smaller than the 262-keV peak and the 171-keV peak is barely above the background. This cannot be explained solely as an effect of detector efficiency and increasing internal conversion with decreasing $\gamma$-ray energy, as a similar gate on the 306-keV transition of $^{232}$U (Fig. 4b) does not show a corresponding drastic drop in counts - the 218-keV peak, for example, is higher than the 265-keV peak, and the 166-keV peak is well above the background. While dipole transitions connecting the favoured signature of Band 1 to the unfavoured signature could in principle cause this loss of intensity, none were observed. These are, however, expected to be highly converted, implying that the $\gamma$-ray intensity could be lost to electrons.

In order to explore this possibility and quantify changes in the E2 $\gamma$-ray strength with decreasing spins, we calculated the ratio

$$\begin{aligned} R=\frac{T_{\gamma ,2}}{(T_{\gamma ,1} + T_{e,1} + T_{e,2} )} \end{aligned}$$

(5)

where $T_{\gamma ,2}$ is the E2 in-band $\gamma$-ray transition rate, $T_{\gamma ,1}$ is the M1 crossover $\gamma$-ray transition rate, and $T_{e,1}$ and $T_{e,2}$ are the respective conversion electron rates for M1 and E2 transitions, formed using the BRICC conversion coefficients [14], $T_{L} = T_{\gamma ,L} (1+\alpha _{T_L})$, where $T_{L}$ is the total transition intensity of multipolarity L. This ratio compares the in-band $\gamma$-ray strength to the total intensity that leaves the band due to decay-out and also conversion, i.e. it is a metric for the attrition of the in-band $\gamma$-ray intensity.

The rotational model was used to calculate the M1 and E2 reduced transition probabilities. For in-band E2 transitions we have

$$\begin{aligned} B(E2) = \frac{5}{16 \pi } Q_{0}^{2} \langle I_{i} K 2 0 | I_{f} K \rangle ^{2}, \end{aligned}$$

where we have used a quadrupole moment of $Q_{0}=9.4$ eb, taken to be the average of $^{230}$U and $^{232}$U [15]. The B(M1) values between between signature partners were calculated using

$$\begin{aligned} B(M1) = \frac{3K^{2}}{4 \pi } \left( g_{K} - g_{R} \right) ^{2} \langle I_{i} K 1 0 | I_{f} K \rangle ^{2}, \end{aligned}$$

(6)

where the parameters $g_{K}$ and $g_{R}$ are the gyromagnetic ratios for the intrinsic state and the collective motion of the core, respectively. It is evident from Eqn. 6 that the expected M1 strength depends strongly on the quantity $\left( g_{K} - g_{R} \right) ^{2} K^2$ (the Clebsch-Gordan coefficients in Eqn. 6 are weak functions of I and K). The $g_{K}$ values used in our calculations, and listed in Table 3, are those calculated by Bengtsson et al. [9] using the Woods-Saxon wave functions. Ward et al. obtained an experimental value $\left( g_{K} - g_{R}\right) = \pm 0.38$ for the $j_{15/2}$ $[743]7/2^{-}$ band of $^{235}$U [16]. Since Band 1 is also associated with the $j_{15/2}$ subshell, we used this result to obtain a value of $g_{R}=0.26$ for this band.

The results in the form of B(M1)/B(E2) values, $\gamma$-ray branching ratios, $\lambda$ and the ratio R are listed Table 4. The B(M1)/B(E2) values are in line with the experimental values of Ward et al. for the $j_{15/2}$ $[743]7/2^{-}$ band, which typically lie around 0.08 ${\mu }_{N}/$eb$^{2}$, when allowance is made for the reduction of K from 7/2 to K=5/2 in the present case. One sees that the branching ratios $\lambda$ decrease down the band, so that magnetic $\Delta I$=1 crossover transitions become increasingly competitive at low spins. When conversion electron rates are included, to form the ratio R, the E2 $\gamma$-ray branch attenuates further. The calculated transition rates allow us to reconstruct the spectrum formed by gating on the 304-keV transition in Band 1. It is shown in red, overlaying the experimental spectrum in Fig. 4a. The simulation, which takes account of the detector lineshape and efficiency, has only one free parameter - the intensity passing through 304-keV transition. This was manually adjusted to reproduce the experimental spectrum. The loss of E2 intensity is well accounted for, as is the strength of the 113-keV line which is assumed to have E1 multipolarity in the simulation. The $\Delta I$=1 crossover transitions between the signature partners of Band 1, enclosed in square brackets in Fig. 1, are not predicted to rise above the background.

4 Discussion

At the time of writing, the ground-state configuration of $^{231}$U had not been firmly established, although $[752]5/2^{-}$ was considered most likely based on $\beta$-decay studies [2] (and references therein). In the present work, however, we have presented evidence that the $[752]5/2^{-}$ band is yrast at medium spin values, and that it decays to a state with the opposite parity via the 113-keV E1 transition, and we consider it likely that this connects to the $[633]5/2^{+}$ band, which is yrast at extremely low spin. We therefore tentatively suggest that the $[633]5/2^{+}$ bandhead is the $^{231}$U ground state, in which case the ground-state spin-parity is $5/2^{+}$. The lowest configurations and energies of the ground states and first excited states in $^{231}$U and adjacent nuclei can be compared in Table 5. We note that if the 113-keV transition is the $5/2^- \rightarrow 5/2^+$ decay, the energy difference between the $[633]5/2^{+}$ and $[752]5/2^{-}$ bands in $^{231}$U is similar to the energy difference in $^{229}$Th.

In the $N \sim 140$ region, both the $1j_{15/2}$ and $2g_{9/2}$ orbitals are located close to the Fermi surface. Such orbitals (with $\Delta N=1$ and $\Delta \ell =\Delta j=3$) are known to be associated with strong octupole correlations. Octupole deformation may therefore be present in the $^{231}$U ground state. One experimental fingerprint (in odd nuclei) is a pair of alternating-parity bands connected by enhanced E1 transitions. For example, $^{229}_{88}$Ra$_{141}$, exhibits strong octupole correlations, and the $[752]5/2^{-}$ and $[633]5/2^{+}$ orbitals are parity partners [17]. As the octupole collectivity weakens along the $N=141$ isotonic chain $^{229}$Ra$-^{231}$Th$-^{233}$U, the $[752]5/2^{-}$ excitation energy increases. $^{229}$Ra is considered to lie within the transitional region to static octupole deformation, whereas $^{233}$U does not [17]. We note that the energy of this state appears to be substantially lower in $^{231}$U than $^{233}$U, based on the present work (see Table 5), suggesting that $^{231}$U may be a more favourable candidate. Nevertheless, the evolution of low-lying configurations for the $N=139$ isotones is poorly known, and the degree of octupole collectivity in $^{231}$U remains an open question. Our data did not reveal evidence of parity partners.

5 Summary

We have reported the first rotational bands in the nucleus $^{231}$U. Our results are based on an extended data set involving $(\alpha$,xn) reactions at beam energies of 42, 52 and 61 MeV, with an emphasis on the 52-MeV data. Three bands are identified with $^{231}$U based on coincident X-rays and experimental excitation functions. Configuration assignments are supported by CSM and B(M1)/B(E2) calculations. The strongest band, Band 1, is yrast and associated with the $\nu [752]5/2^{-}$ Nilsson orbital. The signature partners of this band could be connected via linking transitions. The second strongest, Band 2, is identified as the ground-state band, and is associated with the $\nu [633]5/2^{+}$ orbital while Band 3 is associated with the $\nu [631]3/2^{+}$ configuration. The weaker bands could not be linked to the other structures. The $^{231}$U ground state, previously suggested to be $5/2^{-}$, is suggested to be $5/2^{+}$. The excitation energy of the $\nu [752]5/2^{-}$ band is tentatively suggested to be at least 113.0 keV, based on a strong E1 out-of-band decay, presumably to the ground state.

An interesting question to consider in future experimental work is whether the $^{231}$U ground state exhibits static octupole deformation, as is the case for the isotone $^{229}$Th. However, there were no experimental signatures of reflection asymmetric shapes in our data.