Superallowed beta-decay between isobaric analog states up to ${{\textbf {A}}}=\textbf{99}$

Abstract

Isospin symmetry is used to fit the precisely known $Q_{EC}$-values of lighter $T_Z=0,-1$ and $T_Z=-1/2$ $\beta$-emitters and to extrapolate them up to $Z=50$. For the $\hbox {T}=1$ emitters the half-lives of the pure $0^+\rightarrow 0^+$ Fermi decays are calculated and compared with experimentally known values, even for the heaviest cases where the experimental uncertainties are still rather large. For the $\hbox {T} = 1/2$ emitters only the Fermi component of the transitions can be predicted, but with the experimental half-lives the ratio of Gamow–Teller to Fermi strength can be determined.

1 Introduction

The liquid drop mass formula [1] is very successful but comes to its limits because of the structure of nuclear states. To get to higher precision we have to use nuclear structure models, in general. However, if we are interested in mass differences of nuclei with the “same” nuclear structure, the liquid drop model should still work well. Mass differences are needed for $\beta$-decay Q-values. And nuclei with the “same” structure are members of an isospin multiplet where just one or several protons are replaced by neutrons in the same configuration. Isospin multiplets are well studied for $\hbox {T}=1$, $0^+\rightarrow 0^+$ $\beta$-transitions [2]. Because these are pure Fermi-transitions they are used to test the conserved vector current (CVC) hypothesis and to deduce the first element $V_{ud}$ of the Cabibbo–Kobayashi–Maskawa (CKM) quark mixing matrix. Experimentally, Q-values and partial half-lives are precisely known up to $A\approx 70$. But these $0^+\rightarrow 0^+$ $\beta$ transitions exist up to $A=98$ (e.g. [3]). Therefore, it is my aim to extrapolate electron capture Q-values ($Q_{ EC}$) and half-lives of $\hbox {T}=1$ triplets up to $A=98$. The situation is similar for $\hbox {T}=1/2$ doublets which are also well studied [4]. Here, parent and daughter nuclei, naturally, cannot have spin $\hbox {I}=0$ and also a Gamow-Teller transition is allowed. Nevertheless, we can extrapolate the $Q_{EC}$-values and calculate the partial half-lives for the Fermi-transition up to $\hbox {A}=99$.

Table 1 Experimental and calculated Q$_{EC}$-values for superallowed decays of $\hbox {T}=1$, $\hbox {T}_Z=0,-1$, I$^\pi$=0$^+$ parent nuclei, or the corresponding mass difference if the $\hbox {T}=1$, 0$^+$ is not the ground state of the T$_Z=0$ member of the isospin triplett. Errors are only given if $\Delta Q > 1$ keV. The values for log(f) are taken from the National Nuclear Data Center [5] for the calculated Q-values. With an uncorrected value of $ft=3030+Z$ (see Sect. 3) the half-life is calculated for a superallowed decay. Experimental half-lives (uncorrected for branching) are only given, if the branch is $>99\%$. Errors are given, if $\Delta T_{1/2}/T_{1/2} > 1\%$. The deviation is calculated as $1-T_{1/2}^{calc}/T_{1/2}^{exp}$

2 Q-values

Using the liquid drop mass formula [1] with the binding energy of a nucleus $^AZ$ e.g. written in the form [12]

$$\begin{aligned} BE(^AZ)= & {} a_{v}A-a_s A^{2/3}-a_cZ(Z-1)/A^{1/3}\\{} & {} -a_a(N-Z)^2 /A- \delta a_p/A^{1/2} \end{aligned}$$

one gets for the mass difference between two neighboring isobaric nuclei or the Q-value for electron capture decay:

$$\begin{aligned}{} & {} \Delta M(^AZ;^AZ-1)=Q_{EC}=a_c(2Z_p-2)/A^{1/3}\\{} & {} \quad - 4a_a(N_p-Z_p+1)/A+ 2\delta a_p/A^{1/2}+m_H-m_n \end{aligned}$$

with the constants for Coulomb-energy $a_c$, asymmetry energy $a_a$, pairing energy $a_p$ and $\delta =+1; 0; -1$ for $\hbox {Z,N}=\hbox {odd,odd}; \hbox { A}=odd; Z, N =$ even,even, respectively. $Z_p$ and $N_p$ are proton and neutron number of the parent nucleus. If nuclei are homogeniously charged spheres the Coulomb energy constant should be $a_c=6/5e^2/(4\pi \epsilon _0r_0)$, i.e. inversely proportional to the radius parameter $r_0$.

Fig. 1

Additional binding energy of the $T_Z=0$ member of $T=1$ triplets compared to the $T_Z=\pm 1$ members as a function of the mass number A

Fig. 2

Residua of the fit to the $T=1\ Q_{EC}$-values as a function of the nuclear charge of the parent nucleus $Z_p$

For the $Q_{EC}$ values between members of the $A=4n+2$ and $T=1$ triplets we have to take into account all terms and also that there is a discontinuity for $\hbox {N}=Z$ nuclei, i.e. at $T_Z=0$, which was postulated already by Wigner in 1937 [13]. The mass of the $T_Z=0$ (odd,odd) member is modified by $\Delta M(T_Z=0)=-4a_a/A+a_p/\sqrt{A}-E_W$ where $E_W$ is the Wigner energy. In order to extract the Coulomb term $a_c$ the sum of the Q-values for the $T_Z=-1$ parent and the $T_Z=0$ parent for a given mass number A was fitted as a linear function of the sum of $(Z_{1p}+Z_{2p}-2)/A^{1/3}=(A-1)/A^{1/3}$. Data (see Table 1) were used [2, 6] for $10\le A\le 66$. The result of that fit is that the $T=1$, $T_Z=0$ state is on average stronger bound by 67 keV than the average of the $T=1$, $T_Z=\pm 1$ isospin partners. That means that the Wigner energy more than compensates the pairing term minus the asymmetry term of the T$_Z=\pm 1$ member of the isospin triplet. The individual values for this additional binding are shown in Fig. 1 and I use this constant value independent of A. The result is $Q_{EC}=2a_c(Z_p-1)/A^{1/3}+b\pm c$ with $a_c=699.0$ keV, $b=-1385$ keV and $c= 67$ keV. For the last term the positive (negative) sign is for $T=1, T_Z=-1 \ (T_Z=0)$ parent nuclei. The differences between experimental and fit values are shown in Fig. 2 and their rms deviation amounts to 70 keV. The value of $a_c$ corresponds to a radius parameter for spherical nuclei of $r_0=1.236 fm$. One can recognize discontinuities at $Z_p=8$ and $Z_p=20$, the magic numbers, but not at $Z_p=28$. Apparently, a real theory would have to account for shell effects. It is also obvious that there is a problem at $\hbox {A}=70$ or $Z_p=35,36$. It appears like the experimental mass of $^{70}$Br is too large by some 400 keV. Hardy and Towner [2] already rejected this result [8]. A similar discrepancy has been recognized by Morales et al. [14] in calculating the ft-value for the superallowed decay of $^{70}$Br using the Q-value of AME2020 [6, 8]. (For $^{70}$Br the precise, most recent value [8] deviates by $3.1\sigma$ from the older value of Davids [15] and by $7.6\sigma$ from that of Karny et al. [16]. Note added in proof: a recent evaluation of Coulomb energy differences (Phys. Rev. C 108:034301) comes to a similar conclusion, namely that $^{70}$Br is by 508(22) keV more bound than the adopted value from [16])

Fig. 3

Residua of the fit to the $T=1/2\ Q_{EC}$-values as a function of the charge number of the parent nucleus $Z_p$

For parent nuclei with $Z=N+1$ or $T_Z=-1/2$ the asymmetry and pairing term vanish in $Q_{EC}$. When the well known $Q_{EC}$ values for $T_Z=-1/2$ parent nuclei (see Table 2) are fitted one recognizes a similar staggering between alternate values which was already described by Jaenecke [17, 18]. It can be interpreted as a difference in pairing energy of protons and neutrons. Therefore I fitted the $\hbox {A}=4\hbox {n}+1$ and $\hbox {A}=\hbox {4n}+3$ series separately, as was done already by MacCormick and Audi [19]. The result with a common $a_c$ for $Q_{EC}=2a_c(Z_p-1)/A^{1/3}+b\pm c$ using the Q-values for $7\le A\le 69$ is $a_c=700.45~keV$, $b=-631.0~keV$ and $c=72.9~keV$. Here, the positive (negative) sign of the last term is for $\hbox {A}=4\hbox {n}+3$ ($\hbox {A}=4\hbox {n}+1$) nuclei. This means that the neutron pairing is stronger than the proton pairing. The rms deviation of the thus calculated values from the input values for $7 \le A \le 75$ is 85 keV, and the individual deviations are shown in Fig. 3. Again, discontinuities at the magic numbers 8 and 20 are visible. The calculated Q$_{EC}$-values and those from experiment [6, 11] are given in Table 2.

Table 2 Calculated and experimental Q$_{EC}$-values for the $\hbox {T}=1/2$ mirror decays. The experimental values for $A\le 59$ are from [6], those for $61\le A\le 75$ are weighted averages from [6, 7], and those for $A\ge 91$ are from [11]. The values for the statistical rate function f for $A\le 59$ have been taken from Severijns et al. [4] who used experimental Q-values, and were calculated for $A\ge 61$ from the calculated Q-values. With an uncorrected value of $ft=2*(3030+Z)$ (see Sect. 3) the partial half-life is calculated for the Fermi decay component. The experimental half-lives are those given by [4]. However for $A\ge 63$ they are not corrected for the branches feeding other states than the mirror state. A “p” means that the ground state decays via proton emission. The values for $A\ge 91$ are again from [11]. The last column gives the ratio of Gamow-Teller to Fermi strength (see text)

3 Half-lives

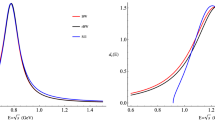
The $0^+\rightarrow 0^+$ transitions of the $T_Z=0$ or $T_Z=-1$ parent nuclei are all pure Fermi transitions and their strength is a constant, when the appropriate radiative, charge dependent and isospin symmetry breaking corrections are applied [2]: ${\mathcal {F}}t=3072.24 \pm 1.85 s$. Here I want to give extrapolations up to $Z=50$ and am neglecting the corrections. Instead, for the slowly increasing ft-values $ft=(3030+Z)s$ (compare Fig. 3a of Ref. [2]) is used. I assume this to be correct within $1\%$. To calculate the half-lives I took the values of log(f) from the National Nuclear Data Center’s internet application [5] using the calculated $Q_{EC}$-values in the case of $\hbox {T}=1$ transitions (see Table 1). The experimental uncertainties for $A\ge 74$ are in the order of 10% and I assume that the calculated half-lives give a better estimate. It turns out that Q-values calculated from measured half-lives are more precise than the measured Q-values. This is shown in Fig. 4 for the heaviest $T_Z=0$ $\beta$-emitters with $39\le Z_p \le 49$. The red circles give the values calculated with the Coulomb energies. The blue triangles are calculated from the half-lives with the ft-values mentioned, the errors are those due to the experimental half-lives. And the squares are the directly measured Q-values from the $\beta$-endpoints for the three heaviest $T_Z=0$ emitters [11].

Because the Fermi strength $B(F)=1$ for $T=1/2$ transitions and $B(F)=2$ for $T=1$ transitions the partial half-life is calculated for the Fermi decay component of $T=1/2$ transitions with an uncorrected value of $ft=2*(3030+Z) s$, double that of $T=1$ transitions. The values for the statistical rate function f have been used from experimental Q-values [4] for $A\le 69$ and for $A\ge 71$ from the calculated Q-values, because then the error bars become $\approx 1 \%$ and larger. The experimental half-lives are those given by [4] and for $A\ge 91$ from [11]. The last column gives the Gamow-Teller to Fermi ratio for the transition

$$\begin{aligned} \rho ^2=T_{1/2}^{Fermi}/T_{1/2}^{exp}-1=(g_A/g_V)^2*B(GT)/B(F) \end{aligned}$$

where $T_{1/2}^{Fermi}=T_{1/2}^{calc}$, and $B(F)=1$ for $T=1/2$ [3, 4]. One has to bear in mind that in nuclear $\beta$-transitions the ratio $g_A/g_V$ is usually assumed to be quenched compared to the value from the $\beta$-decay of the free neutron $g_A/g_V=-1.2754(13)$ [20]. Typically, in shell model calculations $\mid g_A/g_V\mid \approx 1$ is used, thus accounting for correlations or the truncation of the model space. So, the values of $\rho ^2$ could be compared with theoretical values (e.g. V.I. Isakov [21]).

Fig. 4

$Q_{EC}$-values for the heaviest $T_Z=0; 0^+\rightarrow 0^+ \beta$-emitters. The red circles give the values calculated with the Coulomb energies. The blue triangles are calculated from the half-lives with the ft-values mentioned, the errors are those due to the experimental half-lives. And the black squares are the directly measured Q-values from the $\beta$-endpoints for the three heaviest $T_Z=0$ emitters

Summarizing, one can conclude that it is possible to extrapolate $\beta$-decay Q-values between $T=1, T_Z=0,\pm 1$ and $T=1/2, T_Z=\pm 1/2$ isospin partners from the well measured cases with $Z_P\le 30$ up to $Z_P\le 50$. I expect that the uncertainty may increase from about $1\%$ (rms deviation) for the fitted cases to about $2\%$ for the cases with $Z_P\le 50$, i.e. less than 300 keV. Because Fermi $\beta$-decay is so well understood, the half-lives of the heaviest $T=1, 0^+\rightarrow 0^+ \beta$-emitters and the partial half-life for the Fermi component of the $\hbox {T}=1/2$ emitters can be well predicted. Since the $Q_{EC}$-value enters the statistical rate function f with about the 5th to 7th power, I expect an uncertainty of about $15\%$ for the predicted half-lives.