Effect of Nonreciprocal Forces on the Stability of Dust Clusters

Abstract

Results are presented from studies of the stability of the plane dust clusters in the form of a regular polygon with the number of particles from two to five. It is assumed that the particles are placed in the plasma consisting of Maxwellian electrons and a directed flow of cold ions. It is shown that, in such clusters, the oscillatory instabilities can develop along with the aperiodic instabilities. The ranges of plasma parameters are determined, within which the oscillatory instability of the five-particle cluster becomes saturated at the weakly nonlinear stage. As a result, the cluster forms a time crystal, which can be a chiral crystal.

1 INTRODUCTION

In the physics of dusty plasma [1–3], the ensembles of a small number of macroparticles levitating in the near-electrode layer of the gas-discharge plasma are called the clusters [4]. The equilibrium levitation height is determined by the balance between the gravity and electrostatic repulsion of charged particles from the lower electrode. In the horizontal direction, the particle confinement is ensured by the special electrode profiling. Thus, each individual particle is localized in the asymmetric potential well characterized by the oscillation frequencies ${{\Omega }_{0}}$ (in the vertical direction) and ${{\Omega }_{1}}$ (in the horizontal direction).

The distinctive feature of particle interactions is the fact that due to the presence of the directed ion flow in the near-electrode region, the electrostatic potential in the vicinity of the charged particle turns out to be an asymmetric function of coordinates $U(\rho ,z) \ne U(\rho , - z)$ (the z axis is directed vertically). As a result, the interparticle interaction turns out to be nonreciprocal, i.e. the third Newton law is violated. This, in particular, results in the occurrence of correlation between the displacements of individual particles in the vertical and horizontal directions.

Theoretical studies of the dynamics and stability of the plane plasma clusters (for example, [5–9]) were performed under the assumption that the potential of particle interaction is the Coulomb or some other model potential that does not take into account the effect of nonreciprocal forces. This article is the continuation of a series of studies [10–14], in which the dynamics of the two-dimensional ensembles of particles was investigated using the interaction potential calculated numerically. The approach being developed makes it possible to fully take into account the nonreciprocity of interparticle forces.

The dynamics of clusters in the form of a regular polygon, consisting of a small number ($N = 2{-} 5$) of particles, is considered. As is known, in the quasi-two-dimensional plasma crystals, the nonreciprocity of interparticle forces leads to the development of the instability of coupled waves [3]. The nonlinear theory of this instability [14] shows that a time crystal is formed in a certain range of plasma parameters, i.e., in the ground state, the dust particles oscillate near the equilibrium positions. Such instability, which, in this article, is called the oscillatory instability, can also develop in the case of finite clusters.

The article is organized as follows. In Section 2, the model used is briefly described. Next (in Section 3), the linearized equations of motion for the N-particle cluster are reduced to the block-diagonal form. In Section 4, the eigenfrequencies of different clusters are investigated, and the ranges of parameters are determined, within which one or another type of instability develops. Finally, in Section 5, the nonlinear theory is developed for the oscillatory instability of a five-particle-cluster which is of the most interest.

2 MODEL

An ensemble is considered consisting of N particles located in the external potential well ${{U}_{{{\text{ext}}}}}({\mathbf{r}}) =$ $\Omega _{1}^{2}({{x}^{2}} + {{y}^{2}}){\text{/}}2 + \Omega _{0}^{2}{{z}^{2}}{\text{/}}2$. It is believed that the particles have the same constant charges Q and are placed in the plasma consisting of the Maxwellian electrons and the directed flow of cold ions. The corresponding interaction potential has the following form:

$$U({\mathbf{r}}) = \frac{{4\pi {{Q}^{2}}}}{{{{{(2\pi )}}^{3}}}}\int {d{\mathbf{k}}} \frac{{\exp(i{\mathbf{kr}})}}{{{{{\mathbf{k}}}^{2}}\epsilon ( - {\mathbf{ku}},{\mathbf{k}})}},$$

(1)

where ${\mathbf{u}} = (0, - u)$ is the flow velocity. In this case, the dielectric constant of plasma is equal to $\epsilon (\omega ,{\mathbf{k}}) =$ $1 - \omega _{{pi}}^{2}{\text{/}}(\omega (\omega + i\nu )) + 1{\text{/}}({{k}^{2}}\lambda _{{De}}^{2})$, where ${{\omega }_{{pi}}}$ is the ion plasma frequency, ${{\lambda }_{{De}}}$ is the electron Debye radius, and $\nu \to 0$ is the infinitely small collision frequency. The interaction is isotropic in the plane $xy$, i.e., potential (1) has the following form: $U({\mathbf{r}}) = U(\rho ,z)$ ($\rho = \sqrt {{{x}^{2}} + {{y}^{2}}}$). The presence of the directed ion flow results in the fact that $U(\rho , - z) \ne U(\rho ,z)$, i.e., the interparticle forces are nonreciprocal.

We use the dimensionless variables with the length scale $\lambda = u{\text{/}}{{\omega }_{{pi}}}$; the interparticle forces are normalized to ${{Q}^{2}}{\text{/}}{{\lambda }^{2}}$, and the time scale for particles with the mass ${{M}_{0}}$ is $M_{0}^{{1/2}}{{\lambda }^{{3/2}}}{\text{/|}}Q{\text{|}}$. When we use these variables, potential (1) is a function of the distance and also of the only one parameter characterizing the plasma, which is proportional to the Mach number of the ion flow, $M = ({{n}_{e}}{\text{/}}{{n}_{i}})u\sqrt {{{m}_{i}}{\text{/}}{{T}_{e}}}$, where ${{n}_{{e,i}}}$ are the equilibrium densities of electrons and ions, and ${{m}_{i}}$ is the ion mass. The derivatives of the potential are calculated using the numerical methods described in [13].

In equilibrium, the particles are located at the vertices of a regular polygon

$$\begin{gathered} x_{j}^{{(0)}} = R\cos(2\pi j{\text{/}}N), \\ y_{j}^{{(0)}} = R\sin(2\pi j{\text{/}}N), \\ z_{j}^{{(0)}} = {{z}_{0}}\quad (j = 0, \ldots ,N - 1). \\ \end{gathered} $$

(2)

The general equations of motion are as follows:

$${{{\mathbf{\ddot {r}}}}_{j}} = - \nabla {{U}_{{{\text{ext}}}}}({{{\mathbf{r}}}_{j}}) - \sum\limits_{k = 0,k \ne j}^{N - 1} \nabla U({{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{k}}),$$

(3)

where ${{{\mathbf{r}}}_{j}} = ({{x}_{j}},{{y}_{j}},{{z}_{j}})$. Expanding the equations of motion in powers of the small deviations ${{{\mathbf{r}}}_{j}} \to {\mathbf{r}}_{j}^{{(0)}} + {{{\mathbf{r}}}_{j}}$, in the zero-order approximation, we obtain the following equilibrium conditions:

$$\begin{gathered} R\Omega _{1}^{2} + \sum\limits_{j = 1}^{N - 1} \,\sin(j\pi {\text{/}}N)u_{j}^{{1,0}} = 0, \\ {{z}_{0}}\Omega _{0}^{2} + \sum\limits_{j = 1}^{N - 1} \,u_{j}^{{0,1}} = 0, \\ \end{gathered} $$

(4)

where we used the following notations for the derivatives of the interaction potential:

$$u_{j}^{{a,b}} = \mathop {\left. {\frac{{{{\partial }^{{a + b}}}U(\rho ,z)}}{{\partial {{\rho }^{a}}\partial {{z}^{b}}}}} \right|}\nolimits_{\rho = {{d}_{j}},z = 0} $$

(5)

and ${{d}_{j}} = 2R\sin(j\pi {\text{/}}N)$ is the distance from the particle with number j to the particle with number 0.

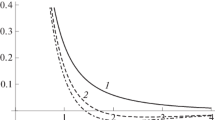
In further consideration, the trap frequencies ${{\Omega }_{{0,1}}}$ and the Mach number M are considered as the external control parameters. The equilibrium cluster radius is calculated using the first of Eqs. (4); it depends on ${{\Omega }_{1}}$ и M. Several examples of how the parameter R depends on M at the fixed frequency ${{\Omega }_{1}}$ are shown in Fig. 1. We note that at $M < 1$ potential (1) turns out to be the attractive potential at considerably large distances [11]. The shape of the potential well bottom in the coordinates (R, M) is shown in Fig. 1 (curve 1). In this case, there may be no external confinement in the transverse direction, and the cluster radius reaches its maximum value at ${{\Omega }_{1}} = 0$. At $M > 1$, the cluster radius indefinitely increases with decreasing frequency ${{\Omega }_{1}}$.

Fig. 1.

Solution ${{u}^{{1,0}}}(r,M) = 0$ as a function of M (1); cluster radii as functions of the Mach number (2–5). Curve number corresponds to the number of particles in the cluster; ${{\Omega }_{1}} = 0.1$.

3 LINEARIZED EQUATIONS OF MOTION

In the first order of expansion of the general equations of motion (3) in powers of the small deviations from equilibrium, we obtain the following equations:

$${{{\mathbf{\ddot {r}}}}_{j}} = \sum\limits_{k = 0}^{N - 1} \,{{{\mathbf{F}}}_{{jk}}} \cdot {{{\mathbf{r}}}_{k}}.$$

In all, there can be $3N$ oscillations with frequencies determined by the eigenvalues of the force matrix $- {{{\mathbf{F}}}_{{jk}}}$. The analysis of the linearized equations of motion can be greatly simplified, if we perform the decomposition into irreducible representations of the symmetry group of the cluster ${{C}_{N}}$ [5]. For the horizontal and vertical displacements, this decomposition looks differently:

$$\begin{gathered} {{x}_{j}} + i{{y}_{j}} = \sum\limits_{l = 0}^{N - 1} \,({{\rho }_{l}} + i{{\phi }_{l}}){{e}^{{i\alpha j(l + 1)}}}, \\ {{z}_{j}} = \sum\limits_{l = 0}^{N - 1} \,{{\zeta }_{l}}{{e}^{{i\alpha jl}}}, \\ \end{gathered} $$

(6)

where $\alpha = 2\pi {\text{/}}N$. Using the formula of finite geometric progression, it is easy to obtain the following inverse transformations:

$$\begin{gathered} {{\rho }_{l}} + i{{\phi }_{l}} = \frac{1}{N}\sum\limits_{j = 0}^{N - 1} \,({{x}_{j}} + i{{y}_{j}}){{e}^{{ - i\alpha j(l + 1)}}}, \\ {{\zeta }_{l}} = \frac{1}{N}\sum\limits_{j = 0}^{N - 1} \,{{z}_{j}}{{e}^{{ - i\alpha jl}}}. \\ \end{gathered} $$

(7)

At $l = 0$ the perturbation with ${{\rho }_{0}} \ne 0$ corresponds to the homogeneous cluster expansion or compression in the xy plane, and the perturbation with ${{\phi }_{0}} \ne 0$ results in the cluster rotation around the z-axis. Since the displacements ${{{\mathbf{r}}}_{j}}$ are real, the transformed parameters ${{{\mathbf{\tilde {r}}}}_{l}} = ({{\rho }_{l}},{{\phi }_{l}},{{\zeta }_{l}})$ meet the obvious correlations ${{{\mathbf{\tilde {r}}}}_{{N - l}}} = {\mathbf{\tilde {r}}}_{l}^{*}$ and ${{{\mathbf{\tilde {r}}}}_{{l + N}}} = {{{\mathbf{\tilde {r}}}}_{l}}$.

After using transformations (6) and (7), the linearized equations of motion (3) can be rewritten in the block-diagonal form:

$${{{\mathbf{\ddot {\tilde {r}}}}}_{l}} = {{{\mathbf{F}}}_{l}} \cdot {{{\mathbf{\tilde {r}}}}_{l}}\quad (l = 0,\; \ldots ,\;N - 1),$$

where the ${{{\mathbf{F}}}_{l}}$ matrix has the following form:

$${{{\mathbf{F}}}_{l}} = \left( {\begin{array}{*{20}{c}} {F_{l}^{{\rho \rho }} - \Omega _{1}^{2}}&{ - iF_{l}^{{\rho \phi }}}&{F_{l}^{{\rho \zeta }}} \\ {iF_{l}^{{\rho \phi }}}&{F_{l}^{{\phi \phi }} - \Omega _{1}^{2}}&{ - iF_{l}^{{\phi \zeta }}} \\ {F_{l}^{{\zeta \rho }}}&{ - iF_{l}^{{\phi \zeta }}}&{F_{l}^{{\zeta \zeta }} - \Omega _{0}^{2}} \end{array}} \right).$$

(8)

The matrix elements included here can be writted as the finite real sums:

$$\begin{gathered} F_{l}^{{\rho \rho }} = - \sum\limits_{j = 1}^{N - 1} \,\left[ {\frac{{u_{j}^{{(1,0)}}}}{R}\frac{{{{\cos}^{2}}(\alpha j{\text{/}}2){{\sin}^{2}}(\alpha jl{\text{/}}2)}}{{\sin(\alpha j{\text{/}}2)}}} \right. \\ \left. {\, + \mathop {2u_{j}^{{(2,0)}}{{\sin}^{2}}(\alpha j{\text{/}}2){{\cos}^{2}}(\alpha jl{\text{/}}2)}\limits_{} } \right], \\ \end{gathered} $$

$$\begin{gathered} F_{l}^{{\rho \phi }} = \frac{1}{2}\sum\limits_{j = 1}^{N - 1} \,\left[ {\frac{{u_{j}^{{(1,0)}}}}{R}\cos(\alpha j{\text{/}}2)\sin(\alpha jl)} \right. \\ \left. {\, + \mathop {u_{j}^{{(2,0)}}\sin(\alpha j)\sin(\alpha jl)}\limits_{} } \right], \\ \end{gathered} $$

$$\begin{gathered} F_{l}^{{\rho \zeta }} = - 2\sum\limits_{j = 1}^{N - 1} \,u_{j}^{{(1,1)}}\sin(\alpha j{\text{/}}2){{\sin}^{2}}(\alpha jl{\text{/}}2), \\ F_{l}^{{\phi \phi }} = - \sum\limits_{j = 1}^{N - 1} \,\left[ {\frac{{u_{j}^{{(1,0)}}}}{R}\sin(\alpha j{\text{/}}2){{\cos}^{2}}(\alpha jl{\text{/}}2)} \right. \\ \end{gathered} $$

(9)

$$\begin{gathered} \left. {\, + \mathop {2u_{j}^{{(2,0)}}{{\cos}^{2}}(\alpha j{\text{/}}2){{\sin}^{2}}(\alpha jl{\text{/}}2)}\limits_{} } \right], \\ F_{l}^{{\phi \zeta }} = \sum\limits_{j = 1}^{N - 1} \,u_{j}^{{(1,1)}}\cos(\alpha j{\text{/}}2)\sin(\alpha jl), \\ \end{gathered} $$

$$\begin{gathered} F_{l}^{{\zeta \rho }} = - 2\sum\limits_{j = 1}^{N - 1} \,u_{j}^{{(1,1)}}\sin(\alpha j{\text{/}}2){{\cos}^{2}}(\alpha jl{\text{/}}2), \\ F_{l}^{{\zeta \zeta }} = - 2\sum\limits_{j = 1}^{N - 1} \,u_{j}^{{(0,2)}}{{\sin}^{2}}(\alpha jl{\text{/}}2). \\ \end{gathered} $$

In the general case, matrix (8) does not have any symmetry properties. However, in the absence of nonreciprocal forces, the derivatives are equal to zero, $u_{j}^{{(1,1)}} = 0$, $F_{l}^{{\rho \phi }} = F_{l}^{{\zeta \rho }} = F_{l}^{{\phi \zeta }} = 0$, and the matrix ${{{\mathbf{F}}}_{l}}$ becomes the Hermitian one. In this case, the equations for the displacements along the z-axis and in the xy plane can be uncoupled and studied independently.

The use of transformations (6) and (7) makes it possible to considerably simplify the problem of searching for the oscillation frequencies and analyzing the stability of dust clusters. All $3N$ oscillations are divided into the groups of three oscillations; each group is characterized by the number l, which corresponds to the wave vector in the infinite systems. We denote the eigenvalues of the matrix $- {{{\mathbf{F}}}_{l}}$ (8) as $\omega {\kern 1pt} {\kern 1pt} {{(N,l,\alpha )}^{2}}$ ($\alpha = 1,\;2,\;3$). These frequencies are the roots of the cubic polynomial $P_{l}^{N}({{\omega }^{2}}) = \det({{\omega }^{2}}{\mathbf{I}} + {{{\mathbf{F}}}_{l}}) = 0$ (I is the unity matrix), and, as can be seen from the structure of matrix (9), the polynomial coefficients are real.

It follows from explicit expressions (9) that ${{{\mathbf{F}}}_{{N - l}}} = {\mathbf{F}}_{l}^{*}$, so the relation $\omega {\kern 1pt} {{(N,l,\alpha )}^{2}} = \omega {\kern 1pt} {{(N,N - l,\alpha )}^{2}}$ is satisfied, i.e., all oscillations with $0 < l < N{\text{/}}2$ are doubly degenerate. This degeneracy occurs due to the fact that some waves propagating in different directions of the ring structure should have the same frequencies. The oscillations with $l = 0$ and $l = N{\text{/}}2$ (for even numbers N) are not degenerate. For this reason, for each cluster consisting of $N$ particles, it is necessary to study the eigenvalues of the matrix ${{{\mathbf{F}}}_{l}}$ for $l = 0,\; \ldots ,\;[N{\text{/}}2]$. For each oscillation mode, the displacements of particles in the cluster are determined by the eigenvectors of the matrix ${{{\mathbf{F}}}_{l}}$ and can be calculated using relations (6).

Two different scenarios are possible for the loss of stability when the external parameters change. First, one of the roots of the characteristic polynomial can change its sign, which corresponds to the development of the aperiodic instability. Second, two real roots $P_{l}^{N}({{\omega }^{2}})$ can merge and form a pair of the complex conjugate roots. In this case, we deal with the oscillatory instability similar to the instability of coupled waves developing in the infinite plasma crystal.

4 EIGENFREQUENCIES

First of all, we notice some general properties of matrix (8). At $l = 0$, the eigenfrequencies can be obtained explicitly for an arbitrary number N. First, there is the neutrally stable mode with $\omega {\kern 1pt} {\kern 1pt} (N,0,1) = 0$, which corresponds to the rigid rotation of the cluster without changing its shape (${{\rho }_{0}} = 0$, ${{\phi }_{0}} \ne 0$, ${{\zeta }_{0}} = 0$). Another oscillation with $\omega {\kern 1pt} (N,0,2) = \pm {{\Omega }_{0}}$ (${{\rho }_{0}} = 0$, ${{\phi }_{0}} = 0$, ${{\zeta }_{0}} \ne 0$) corresponds to the vertical oscillations of the center of mass of the cluster without changing its shape. Finally, the third mode has the following frequency:

$$\begin{gathered} \omega {\kern 1pt} {\kern 1pt} {{(N,0,3)}^{2}} \\ \, = \sum\limits_{j = 1}^{N - 1} \,\left[ {2u_{j}^{{2,0}}si{{n}^{2}}(j\pi {\text{/}}N) - \frac{{u_{j}^{{1,0}}}}{R}\sin(j\pi {\text{/}}N)} \right]. \\ \end{gathered} $$

(10)

For this oscillation mode, the particles are displaced along the straight lines (Fig. 2). In this case, the horizontal components of the displacements are parallel to vectors ${\mathbf{r}}_{j}^{0}$ (2), and all their vertical components are equal. Although the frequency (10) does not depend on ${{\Omega }_{0}}$, the slope of the displacements is determined just by ${{\Omega }_{0}}$. In all the cases that have been studied, the square of frequency (10) turns out to be positive, and no instabilities arise associated with the excitation of the symmetric oscillations. In what follows, the oscillations with $l = 0$ are not specially discussed.

Fig. 2.

An example of particle displacements for the mode with $l = 0$.

In the case of oscillations with $l = 1$, one of the frequencies of a cluster consisting of $N$ particles coincides with the frequency of the trap $\omega {\kern 1pt} {{(N,1,3)}^{2}} = \Omega _{1}^{2}$, i.e., the characteristic polynomial can be written as a product $P_{1}^{N}({{\omega }^{2}}) = ({{\omega }^{2}} - \Omega _{1}^{2})P_{1}^{{'N}}({{\omega }^{2}})$. In this case, the shape of the cluster does not change; all particles are in the xy plane, and the center of mass oscillates in an arbitrary direction with the frequency ${{\Omega }_{1}}$. The frequencies and polarizations of the other two oscillation modes with $l = 1$ depend on the number of particles in the cluster.

4.1 Two Particles

In the case of a cluster consisting of two particles, the oscillation $l = 1$ with the frequency ${{\Omega }_{1}}$ turns out to be doubly degenerate. The frequency of the remaining oscillation is equal to $\omega {\kern 1pt} {{(2,1,1)}^{2}} = \Omega _{0}^{2} + 2u_{1}^{{0,2}}$, and the particle displacements are proportional, ${{{\mathbf{r}}}_{1}} = (x,0,z)$ and ${{{\mathbf{r}}}_{2}} = (x,0, - z)$. The condition that the quantity $\omega {\kern 1pt} {\kern 1pt} {{(2,1,1)}^{2}} > 0$ should be positive determines the frequency range of the cluster stability: ${{\Omega }_{0}} > {{\Omega }_{{{\text{cr}}}}}$. An example of the ${{\Omega }_{{{\text{cr}}}}}$(M) dependence constructed using potential (1) is shown in Fig. 3 (solid line). As the ${{\Omega }_{0}}$ frequency decreases to the ${{\Omega }_{{{\text{cr}}}}}$ frequency, there occurs a tendency to the formation of the vertical chain of particles; in this case, due to nonreciprocity of the interparticle forces, both particles are displaced in the same direction along the $x$-axis.

Fig. 3.

Critical frequencies for $N = 2$ and $N = 3$ (solid and dashed lines, respectively); ${{\Omega }_{1}} = 0.1$.

4.2 Three Particles

In the case of three particles, the only nontrivial mode is characterized by the number $l = 1$. The roots of the quadratic equation $P_{1}^{{'3}}({{\omega }^{2}}) = 0$ are as follows:

$${{\omega }^{2}} = \frac{1}{4}\left( {2\Omega _{0}^{2} + \Omega _{1}^{2} + 6u_{1}^{{0,2}} \pm \sqrt D } \right),$$

(11)

where $D\,\; = \,\;{{(2\Omega _{0}^{2} - \,\;\Omega _{1}^{2} + \,\;6u_{1}^{{0,2}} + \,\;3u_{1}^{{2,0}})}^{2}} + \,\;24{{(u_{1}^{{1,1}})}^{2}}$. Since the parameter D is positive, $D > 0$, both solutions (11) are real, but one of them can become negative with decreasing frequency ${{\Omega }_{0}}$. The corresponding critical frequency ${{\Omega }_{0}}$ is shown in Fig. 3 (dashed curve). When the aperiodic instability develops, the vertical displacements of two arbitrary particles are directed opposite to the displacement of the third one, for example, ${{{\mathbf{r}}}_{1}} = ({{x}_{1}},0,{{z}_{1}})$, ${{{\mathbf{r}}}_{2}} = ({{x}_{2}},{{y}_{2}}, - {{z}_{1}}{\text{/}}2)$, and ${{{\mathbf{r}}}_{2}} = ({{x}_{2}}, - {{y}_{2}}, - {{z}_{1}}{\text{/}}2)$. In this case, the horizontal displacements ${{x}_{{1,2}}}$ have the same sign. Thus, during the development of the aperiodic instability of the three-particle cluster, a tendency is observed to the formation of a three-dimensional structure.

4.3 Four Particles

In contrast to the examples considered above, the dynamics of a four-particle cluster is determined by the potential derivatives at two distances: ${{d}_{1}} = \sqrt 2 R$ and ${{d}_{2}} = 2R$. For this reason, the explicit formulas for the frequencies turn out to be more cumbersome, and in further consideration, we will restrict ourselves to a qualitative discussion of the cluster stability regions.

In the case $l = 1$, the eigenfrequencies of oscillations that remain after we have considered the solution with $\omega {\kern 1pt} {\kern 1pt} {{(4,1,3)}^{2}} = \Omega _{1}^{2}$ are determined by the roots of the quadratic equation $P_{1}^{{'4}}({{\omega }^{2}}) = 0$. These roots will be the complex ones, if the following two conditions are satisfied:

$$\nu = - u_{1}^{{1,1}}u_{2}^{{1,1}} > 0$$

(12)

and

$$\Omega _{{{\text{cr}},2}}^{2} < \Omega _{0}^{2} < \Omega _{{{\text{cr}},1}}^{2},$$

(13)

where

$$\Omega _{{{\text{cr}},1,2}}^{2} = 2u_{1}^{{2,0}} - 2u_{1}^{{0,2}} - 2u_{2}^{{0,2}} - \frac{{u_{2}^{{1,0}}}}{R} \pm {{2}^{{7/4}}}\sqrt \nu .$$

(14)

At the boundary of the domain defined by inequalities (12) and (13), two real roots merge, and the frequencies of coupled oscillations are determined by the following relations:

$$\omega {\kern 1pt} {\kern 1pt} {{(4,1,1)}^{2}} = \omega {\kern 1pt} {\kern 1pt} {{(4,1,2)}^{2}} = 2u_{1}^{{2,0}} - \frac{{u_{2}^{{1,0}}}}{R} - {{2}^{{3/4}}}\sqrt \nu .$$

(15)

For the coupled oscillations at the boundary of the instability domain, the particle trajectories are shown in Fig. 4. The particles move circularly around the equilibrium position in the plane tilted at some angle to the xy plane. As already noted, the oscillation frequencies with $l = 1$ and $l = 3$ coincide, but in the latter case, the direction of particle motion is opposite.

Fig. 4.

Oscillatory instability of four-particle cluster. Solid arrows correspond to instantaneous displacements of particles; dashed ellipses are trajectories of particles during one oscillation period; $l = 1$, $M = 1.1$, ${{\Omega }_{0}} \approx 0.21$, and ${{\Omega }_{1}} = 0.1$.

The similar dynamics is observed for oscillations with $l = 2$. There is the stable oscillation with the frequency $\omega {\kern 1pt} {\kern 1pt} {{(4,2,3)}^{2}} = 2u_{1}^{{2,0}} - \sqrt 2 u_{1}^{{1,0}}{\text{/}}R$, for which the particle displacements shown in Fig. 5a are in the horizontal plane and do not depend on the external control parameters. The two remaining coupled oscillations can become unstable, if inequalities (12) and (13) become satisfied. In this case, the critical values of the parameter ${{\Omega }_{0}}$ will change as follows:

$$\Omega _{{{\text{cr}},1,2}}^{2} = 2u_{2}^{{2,0}} - 4u_{1}^{{0,2}} - \frac{{u_{2}^{{1,0}}}}{R} \pm {{2}^{{9/4}}}\sqrt \nu .$$

(16)

Fig. 5.

Oscillations of four-particle cluster with $l = 2$: (a) stable horizontal oscillations, and (b) oscillations with parameters corresponding to the boundary of the region of the oscillatory instability development; $M = 1.07$, ${{\Omega }_{0}} \approx$ 0.23, and ${{\Omega }_{1}} = 0.1$.

The frequencies of coupled oscillations at the boundary parameters of the oscillatory instability development are as follows:

$$\omega {\kern 1pt} {\kern 1pt} {{(4,2,1)}^{2}} = \omega {\kern 1pt} {\kern 1pt} {{(4,2,2)}^{2}} = 2u_{1}^{{2,0}} - \frac{{u_{2}^{{1,0}}}}{R} + {{2}^{{5/4}}}\sqrt \nu ,$$

(17)

and the displacements of particles occur along the straight lines inclined at the same angles to the xy plane (Fig. 5b).

If one of inequalities (12) or (13) is violated, the roots of the characteristic equation become real. However, for both $l = 1$ and $l = 2$, the square of one of the frequencies can become negative, which results in the development of the aperiodic instability. For the four-particle cluster, the resultant stability diagram is shown in Fig. 6. At the boundary of the region ${{A}_{2}}$, the aperiodic instability of the mode with $l = 2$ develops; an example of the particle displacements is shown in Fig. 7. The region of the aperiodic instability development for the mode with $l = 1$ (the region ${{A}_{1}}$ in Fig. 6) is entirely inside the region ${{A}_{2}}$.

Fig. 6.

Stability diagram of the four-particle cluster: ${{A}_{{1,2}}}$ are regions of the aperiodic instability development and ${{O}_{{1,2}}}$ are regions of the oscillatory instability development at $l = 1,2$; ${{\Omega }_{1}} = 0.1$.

Fig. 7.

Particle displacements at the boundary of the region ${{A}_{2}}$ in Fig. 6; $M = 0.8$, ${{\Omega }_{0}} \approx 0.54$, and ${{\Omega }_{1}} = 0.1$.

The regions ${{O}_{{1,2}}}$ of the oscillatory instability development are small. They are shown on the enlarged scale in Fig. 6 on the right. These regions correspond to the same domain of variation of the parameter M, determined by the first inequality (12), and partially overlap.

4.4 Five Particles

In the case of five particles, the cluster dynamics is determined by the derivatives of the interaction potential at two distances: ${{d}_{1}} = R\sqrt {(5 - \sqrt 5 ){\text{/}}2}$ and ${{d}_{2}} = R\sqrt {(5 + \sqrt 5 ){\text{/}}2}$. The explicit expressions for the frequencies turn out to be very cumbersome, but can be easily calculated using the numerical methods.

Just as in the case of the four-particle cluster, it is necessary to study the modes with $l = 1$ and $l = 2$. The cluster stability diagram is shown in Fig. 8. At the boundary of the region ${{A}_{2}}$, the aperiodic instability of the mode with $l = 2$ develops; in this case, two arbitrary neighboring particles leave the xy plane in the course of their displacement, and the other three displace in the opposite direction. The region ${{A}_{1}}$ of the aperiodic instability development for the mode with $l = 1$ is entirely inside the region ${{A}_{2}}$.

Fig. 8.

Stability diagram of the five-particle cluster: ${{A}_{{1,2}}}$ are regions of the aperiodic instability development, and ${{O}_{{1,2}}}$ are regions of the oscillatory instability development at $l = 1,2$; ${{\Omega }_{1}} = 0.1$.

In contrast to the case of the four-particle cluster (Fig. 6), the regions ${{O}_{{1,2}}}$ corresponding to the development of the oscillatory instability occupy a considerable part of the stability diagram. For both types of the coupled oscillations with $l = 1,2$ (the ${{O}_{{1,2}}}$ regions in Fig. 8), the particles move in circular orbits in the vicinity of the equilibrium positions (Figs. 9 and 10). Their motions differ in the amplitudes and phases of particle displacements. It turns out that both regions ${{O}_{{1,2}}}$ consist of two parts. The two parts of the ${{O}_{2}}$ region are separated by a narrow “slit” corresponding to the range $1.16 < M < 1.2$; therefore, it is rather difficult to reach the regions ${{O}_{1}}$ under conditions of the poorly controlled changes in the control parameters.

Fig. 9.

Particle trajectories at the boundary of the region of the oscillatory instability development; $l = 1$, $M = 1.1$, ${{\Omega }_{0}} \approx 0.22$, ${{\Omega }_{1}} = 0.1$, and $\omega \approx 0.03$.

Fig. 10.

Particle trajectories at the boundary of the region of the oscillatory instability development; $l = 2$, $M = 1.5$, ${{\Omega }_{0}} \approx 0.23$, ${{\Omega }_{1}} = 0.1$, and $\omega \approx 0.07$.

4.5 Open-Boundary Clusters

As already noted, in the subsonic or pure ion flow with $M < 1$, in the horizontal direction, interaction potential (1) turns out to be either the attractive potential (at the considerably large interparticle distances), or the repulsive one (at small distances). In this case, the clusters can exist even in the absence of the radial confinement, ${{\Omega }_{1}} = 0$. The structure and dynamics of such clusters have some specific features.

The bottom of the potential well is located at the distance ${{R}_{0}}$ determined as the solution to the equation ${{U}_{{,\rho }}}(\rho ,0) = 0$. The shape of the potential well in the (R, M) coordinates is shown in Fig. 1 (curve 1).

In accordance with conditions (4), at ${{\Omega }_{1}} = 0$, in the case of the two-particle cluster, the maximum radius is $R = {{R}_{0}}{\text{/}}2$, and for the three-particle cluster, it is $R = {{R}_{0}}{\text{/}}\sqrt 3$. The formulas for the oscillation frequencies given in Sections 4.1, 4.2 are also applicable in the case of ${{\Omega }_{1}} = 0$. When the ${{\Omega }_{0}}$ parameter decreases to a certain critical value (Fig. 11), the aperiodic instability develops. An interesting feature of this instability is that, in contrast to the case of ${{\Omega }_{1}} \ne 0$, at ${{\Omega }_{0}} = {{\Omega }_{{{\text{cr}}}}}$, the vertical displacements of the particles vanish. In this case, at the boundary of the region of the aperiodic instability development, the two- and three-particle clusters begin accelerating in the horizontal direction without changing their shape, that is, they behave like molecular motors.

Fig. 11.

Critical frequencies for $N = 2$ and $N = 3$ (solid and dashed lines, respectively); ${{\Omega }_{1}} = 0$.

Because of equilibrium condition (4), in the case of four particles located at the vertices of a square, at ${{\Omega }_{1}} = 0$, the inequalities $\sqrt 2 R < {{R}_{0}} < 2R$ are satisfied, i.e., the nearest particles repel each other, and the opposite ones attract each other. Obviously, such a configuration is unstable even in the case of two-dimensional motion (${{\Omega }_{0}} \to \infty$), and the square tends to transform into a rhomb. Similar situation arises when the cluster has the form of a regular pentagon.

Thus, in the absence of the radial confinement, the clusters in the form of a regular polygon may exist only when the number of particles is two or three.

In conclusion of this section, we note that the clusters with a large number of particles ($N \geqslant 6$) always turn out to be unstable. Apparently, this is a general law: all known examples indicate that the two-dimensional clusters in the form of a regular polygon exist only for $N \leqslant 5$. For example, in the case of the Coulomb interaction and the two-dimensional motion (${{\Omega }_{0}} \to \infty$) of six particles, the only stable configuration has the form of a regular pentagon with an additional particle in its center [5].

5 NONLINEAR STAGE OF OSCILLATORY INSTABILITY

As can be seen in Figs. 6 and 8, when varying the external control parameters $({{\Omega }_{0}},{{\Omega }_{1}},M)$, the boundary of the region of the oscillatory instability development can be most easily reached for the mode $l = 2$ of the five-particle cluster (the ${{O}_{2}}$ region in Fig. 8). For this reason, we restrict ourselves to discussing the nonlinear dynamics of the cluster with $N = 5$.

The standard Krylov–Bogolyubov method is used to derive nonlinear equations. We set ${{\Omega }_{0}} = {{\Omega }_{{{\text{cr}}}}} + {{\varepsilon }^{2}}\delta$, where $\varepsilon \ll 1$ is a small parameter. When approaching the boundary of the ${{O}_{2}}$ region (Fig. 8) from above, the parameter δ vanishes, and at $\delta < 0$, the instability develops. At the lower boundary of the ${{O}_{2}}$ region the reversed situation occurs: the instability develops at δ > 0.

After substituting ${{{\mathbf{r}}}_{j}} \to {\mathbf{r}}_{j}^{{(0)}} + \varepsilon {{{\mathbf{r}}}_{j}}$ into the initial equations of motion (3), they are expanded in powers of $\varepsilon$ up to the third order, and then transformations (6) and (7) are used. As a result, we obtain equations in the following form:

$${{{\mathbf{\tilde {\ddot {r}}}}}_{l}} = {{{\mathbf{F}}}_{l}} \cdot {{{\mathbf{\tilde {r}}}}_{l}} + \varepsilon {\mathbf{F}}_{l}^{2} + {{\varepsilon }^{2}}{\mathbf{F}}_{l}^{3},$$

(18)

where the matrix ${{{\mathbf{F}}}_{l}}$ is given by formula (8). The matrices ${\mathbf{F}}_{l}^{2}$ are the quadratic functions of ${{{\mathbf{\tilde {r}}}}_{l}}$, and the matrices ${\mathbf{F}}_{l}^{3}$, in addition to the cubic expansion terms, contain a linear term proportional to δ.

We try the solution to Eqs. (18) in the form of the following expansion:

$$\begin{gathered} {{{{\mathbf{\tilde {r}}}}}_{l}} = {{\delta }_{{l,0}}}{{A}_{0}}(\tau ){{{\mathbf{P}}}_{0}} + {{\delta }_{{l,2}}}\left[ {{{e}^{{ - i{{\omega }_{0}}t}}}{{A}_{1}}(\tau ) + {{e}^{{i{{\omega }_{0}}t}}}{{A}_{2}}(\tau )} \right]{\mathbf{P}} \\ \, + {{\delta }_{{l,3}}}\left[ {{{e}^{{ - i{{\omega }_{0}}t}}}A_{2}^{*}(\tau )(\tau ) + {{e}^{{i{{\omega }_{0}}t}}}A_{1}^{*}(\tau )} \right]{\mathbf{P}}\text{*} \\ \, + \sum\limits_{s = - 2}^2 \,{{e}^{{is{{\omega }_{0}}t}}}[\varepsilon {{{\mathbf{B}}}_{{s,l}}}(\tau ) + {{\varepsilon }^{2}}{{{\mathbf{C}}}_{{s,l}}}(\tau )], \\ \end{gathered} $$

(19)

where $\tau = \varepsilon t$ is the slow time. In expansion (19), we set ${{{\mathbf{P}}}_{0}} = (0,1,0)$ and ${{A}_{0}}(\tau )$ is the real slowly varying amplitude, i.e., the first term of the expansion describes the slow rotation of the cluster around the z-axis. The complex amplitudes ${{A}_{{1,2}}}(\tau )$ correspond to the perturbations propagating in different directions of the ring structure. The frequency ${{\omega }_{0}}$ is a doubly degenerate root of the dispersion equation $\det(\omega _{0}^{2}{\mathbf{I}} + {{{\mathbf{F}}}_{2}}) = 0$ at ${{\Omega }_{0}} = {{\Omega }_{{{\text{cr}}}}}$, and ${\mathbf{P}}$ is the corresponding eigenvector, i.e., $(\omega _{0}^{2}{\mathbf{I}} + {{{\mathbf{F}}}_{2}}) \cdot {\mathbf{P}} = 0$. The corrections ${{{\mathbf{B}}}_{{s,l}}}(\tau )$ and ${{{\mathbf{C}}}_{{s,l}}}(\tau )$ to be determined should be real, which follows from the correlations ${{{\mathbf{\tilde {r}}}}_{{5 - l}}} = {\mathbf{\tilde {r}}}_{l}^{*}$.

After substituting expansion (19) into Eqs. (18), the zero term of the expansion in powers of $\varepsilon$ vanishes. The next term of the expansion makes it possible to express the corrections ${{{\mathbf{B}}}_{{s,l}}}(\tau )$ in terms of the derivatives of the ${{A}_{{0,1,2}}}(\tau )$ amplitudes and their quadratic combinations. The existence condition for the solution for the corrections ${{{\mathbf{C}}}_{{s,l}}}(\tau )$ leads to the following set of equations for the amplitudes:

$$\begin{gathered} {{{\ddot {A}}}_{1}} = - \beta \delta {{A}_{1}} - {{\gamma }_{1}}{{A}_{1}}{\text{|}}{{A}_{1}}{{{\text{|}}}^{2}} - {{\gamma }_{2}}{{A}_{1}}{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}} - {{\gamma }_{3}}{{A}_{1}}{{{\dot {A}}}_{0}}, \\ {{{\ddot {A}}}_{2}} = - \beta \delta {{A}_{2}} - {{\gamma }_{1}}{{A}_{2}}{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}} - {{\gamma }_{2}}{{A}_{2}}{\text{|}}{{A}_{1}}{{{\text{|}}}^{2}} + {{\gamma }_{3}}{{A}_{2}}{{{\dot {A}}}_{0}}, \\ \end{gathered} $$

(20)

$${{\ddot {A}}_{0}} = \alpha \frac{d}{{d\tau }}\left( {{\text{|}}{{A}_{1}}{{{\text{|}}}^{2}}\; - \;{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}}} \right).$$

(21)

The explicit expressions for the coefficients α, β, and ${{\gamma }_{i}}$ are too cumbersome, but they can be calculated using the numerical methods. We note that the β coefficient is always positive at the upper boundary of the ${{O}_{2}}$ region in Fig. 8 and always negative at its lower boundary. The rest of the coefficients can change sign when changing the parameters M and ${{\Omega }_{1}}$.

The physical meaning of Eqs. (20) and (21) is quite clear. In the linear stage, the presence of the terms proportional to β leads to (depending on the sign of δ) either an exponential increase in the amplitudes or the slow oscillations. The rest of the terms describe the parametric interaction of the oscillations with the amplitudes ${{A}_{{1,2}}}$ and their correlation with the cluster rotation in the horizontal plane, described by the amplitude ${{A}_{0}}$. According to Eq. (21), the cluster rotation occurs due to the inequality of the amplitudes ${\text{|}}{{A}_{1}}{\text{|}} \ne {\text{|}}{{A}_{2}}{\text{|}}$.

Assuming that there is no rotation at the initial time, we integrate Eq. (21):

$${{\dot {A}}_{0}} = \alpha \left( {{\text{|}}{{A}_{1}}{{{\text{|}}}^{2}}\; - \;{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}}} \right).$$

(22)

Then Eq. (20) can be rewritten in the following form

$${{\ddot {A}}_{i}} = - \frac{{\partial U}}{{\partial A_{i}^{*}}}\quad (i = 1,2),$$

(23)

where

$$U = \beta \delta ({\text{|}}{{A}_{1}}{{{\text{|}}}^{2}}\; + \;{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}}) + \frac{{\gamma _{1}^{'}}}{2}({\text{|}}{{A}_{1}}{{{\text{|}}}^{4}}\; + \;{\text{|}}{{A}_{2}}{{{\text{|}}}^{4}}) + \gamma _{2}^{'}{\text{|}}{{A}_{1}}{{{\text{|}}}^{2}}{\text{|}}{{A}_{2}}{{{\text{|}}}^{2}},$$

(24)

and $\gamma _{1}^{'} = {{\gamma }_{1}} + \alpha {{\gamma }_{3}}$, $\gamma _{2}^{'} = {{\gamma }_{2}} - \alpha {{\gamma }_{3}}$.

For considerably large amplitudes ${{A}_{{1,2}}}$, effective potential (24) is positive when two following conditions are met:

$$\gamma _{1}^{'} > 0,\quad \gamma _{1}^{'} + \gamma _{2}^{'} > 0.$$

(25)

If one of these inequalities is violated, then the solution to Eqs. (23) will tend to infinity during finite time, i.e., the instability development becomes explosive.

We are interested in the stationary solutions to Eq. (23) in the region of the instability development $\beta \delta < 0$. When inequalities (25) are satisfied, there are several nonzero solutions to the equations $\partial U{\text{/}}\partial A_{i}^{*} = 0$. First, there is the following solution with equal amplitudes:

$${\text{|}}A_{1}^{0}{\text{|}} = {\text{|}}A_{2}^{0}{\text{|}} = - \frac{{\beta \delta }}{{\gamma _{1}^{'} + \gamma _{2}^{'}}}.$$

(26)

Substituting ${{A}_{i}}(\tau ) = A_{i}^{0} + \delta {{A}_{i}}(\tau )$ into Eqs. (23) and keeping the linear terms of the expansion in powers of $\delta {{A}_{i}}$, we easily obtain that stationary solution (26) will be stable, if the following condition is satisfied:

$${\text{|}}\gamma _{2}^{'}{\text{|}} < \gamma _{1}^{'}.$$

(27)

We note that, for the solution (26), angular velocity (22) of the cluster rotation vanishes.

Second, there are stationary solutions, for which one of the amplitudes is zero, for example:

$${\text{|}}A_{1}^{0}{{{\text{|}}}^{2}} = - \frac{{\beta \delta }}{{\gamma _{1}^{'}}},\quad {\text{|}}A_{2}^{0}{\text{|}} = 0.$$

(28)

This solution will be stable, if the following condition is satisfied:

$$\gamma _{2}^{'} > \gamma _{1}^{'}.$$

(29)

Of course, the amplitudes ${{A}_{1}}$ and ${{A}_{2}}$ in solutions (28) can be permuted. In solutions (28), angular velocity (22) does not vanish, and the direction of rotation depends on the sign of α and on which of the amplitudes is zero.

Thus, during the development of oscillatory instability of the cluster, different stationary states arise. The parametric interaction can result in the fact that the amplitudes of the perturbations are equal and the rigid rotation of the cluster does not occur. In this case, the cluster particles oscillate along the straight lines, as it is shown in Fig. 2; however, the directions of their trajectories depend on the external parameters.

It is also possible that only one of the perturbation amplitudes is nonzero; then the particles circularly move around the equilibrium positions (Fig. 10), and the rigid rotation of the cluster around the z-axis occurs at the constant angular velocity. Which of the amplitudes ${{A}_{{1,2}}}$ is non- zero and the direction of rotation are determined by random factors. In this case, the cluster becomes the chiral one.

The coefficients $\gamma _{1}^{'}$ and $\gamma _{2}^{'}$ at the upper boundary of the O₂ region (Fig. 8) as functions of the Mach number M (calculated numerically using potential (1)) are shown in Fig. 12. At $M < {{M}_{0}} \approx 1.33$, the coefficient is negative, $\gamma _{1}^{'} < 0$, i.e., in accordance with inequalities (25), there are no stationary states and the instability development is explosive. In particular, in the entire left part of the ${{O}_{2}}$ region (Fig. 8) this coefficient is negative.

Fig. 12.

Coefficients $\gamma _{1}^{'}$ (1) and $\gamma _{2}^{'}$ (2) as functions of the Mach number M at the upper boundary of the ${{O}_{2}}$ region (Fig. 8); ${{\Omega }_{1}} = 0.1$.

In the ranges ${{M}_{0}} < M < {{M}_{1}} \approx 1.63$ and M > ${{M}_{2}} \approx 1.88$, inequality (29) is true, i.e., the instability becomes saturated in the weakly nonlinear stage. In the stationary state, the clusters become chiral, and the amplitude of the oscillations is determined by expressions (28). In the range ${{M}_{1}} < M < {{M}_{2}}$, the amplitudes of both oscillations are determined by expression (26), and the chirality disappears.

6 CONCLUSIONS

In this work, the theory is developed of the stability of finite dust particle clusters in the near-electrode plasma layer, which takes into account the nonreciprocal nature of the forces. The clusters in the form of a regular polygon are considered with the number of particles from two to five. The ranges of plasma parameters are determined, within which the aperiodic instabilities develop, which result in the formation of three-dimensional structures.

For the clusters consisting of four or five particles, the development of the oscillatory instability is possible, which is similar to the instability of coupled waves developing in the infinite crystals. In a certain range of plasma parameters, as a result of the instability development in the five-particle cluster, an analogue of the time crystal forms that is chiral.