Skip to main content
SpringerLink
Log in

An Ensemble of Brownian Particles and a Stochastic Description of a System of “Slow” Convective Thermals at Convection Level

  • DEVELOPMENT OF METHODS OF HYDROPHYSICAL HYDRODYNAMICS
  • Published:
Water Resources Aims and scope Submit manuscript

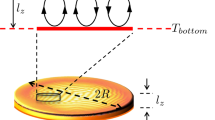
Abstract

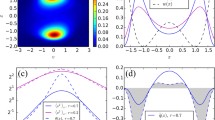
A system of slow convective thermals is considered in a vicinity of convection level. It is shown that a system of spherical convective thermals of fixed radius can be described by a stochastic equation, which is practically identical to Langevin equation for an ensemble of classical Brownian particles. Under the proposed approach, it was shown that the mean vertical velocity of a system of thermals at the convection level is zero. A kinetic analogue of thermodynamic temperature, corresponding to the second moment of the vertical velocity, was shown to exist for a system of thermals. Moreover, the associated Fokker–Planck equation for the system of slow convective thermals has a stationary solution corresponding to generalized Maxwell distribution over vertical velocities. Numerical and field experiments convincingly show that the generalized Maxwell equations is in agreement with the results of calculations and atmospheric measurements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.

Similar content being viewed by others

REFERENCES

  1. Vul’fson, A.N., Equations of deep convection in dry atmosphere, Izv. Akad. Nauk SSSR, Fiz. Atmos. Okeana, 1981, vol. 17, no. 8, pp. 873–876.

    Google Scholar 

  2. Vul’fson, A.N. and Borodin, O.O., Ensemble of convective thermals as generalized analysis of Brownian particles, Usp. Fiz. Nauk, 2016, vol. 162, no. 2, pp. 113–124.

    Article  Google Scholar 

  3. Vul’fson, A.N. and Borodin, O.O., On the stability of Maxwell distribution for a system of thermals in turbulent convective layers of fresh and salt water bodies, Water Resour., 2016, vol. 43, no. 1, pp. 66–72.

    Article  Google Scholar 

  4. Vul’fson, A.N. and Borodin, O.O., The Fokker–Planck equation and statistical characteristics of penetrative convection in the upper ocean, Dokl. Earth Sci., 2011, vol. 440, no. 1, pp. 1287–1290.

    Article  Google Scholar 

  5. Klimontovich, Yu.L., Statisticheskaya teoriya otkrytykh sistem (Statistical Theory of Open Systems), Moscow: Yanus, 1995.

  6. Caughey, S.J., Kitchen, M., and Leighton, J.R., Turbulence structure in convective boundary layers and implications for diffusion, Boundary-Layer Meteor., 1983, vol. 25, no. 4, pp. 345–352.

    Article  Google Scholar 

  7. Caughey, S.J. and Palmer, S.G., Some aspects of turbulence structure through the depth of the convective boundary layer, Quart. J. R. Meteorol. Soc., 1979, vol. 105, pp. 811–827.

    Article  Google Scholar 

  8. Deardorff, J.W., Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection, J. Atmos. Sci., 1970, vol. 27, no. 8, pp. 1211–1212.

    Article  Google Scholar 

  9. Deardorff, J.W. and Willis, G.E., Further results from a laboratory model of the convective planetary boundary layer, Bound.-Layer Meteor., 1985, vol. 32, pp. 205–236.

    Article  Google Scholar 

  10. Du, S., Wilson, J.D., and Yee, E., On moments approximation method for constructing a Lagrangian stochastic model, Bound.-Layer Meteorol., 1993, vol. 63, pp. 65–96, 1994, vol. 40, pp. 2739–292.

  11. Fedorovich, E., Nieuwstadt, F.T.M., and Kaiser, R., Transition regimes and development of the mixed layer, Pt. I, J. Atmos. Sci., 2001, vol. 58, pp. 70–86.

    Article  Google Scholar 

  12. Hibberd, M.F. and Sawford, B.L., A saline laboratory model of the planetary convective boundary layer, Bound.-Layer Meteorol., 1993, vol. 63, pp. 65–96., 1994, vol. 67, pp. 229–250.

  13. Huppert, H.E. and Turner, J.S., Double-diffusive convection, J. Fluid Mech., 1981, vol. 106, pp. 299–329.

    Article  Google Scholar 

  14. Lamb, R.G., Diffusion in the convective boundary layer, Atmospheric Turbulence and Air Modelling, Nieuwstadt, F.T.M., and H. van Dop, D., Boston: Reidel Publication Company, 1982, pp. 159–229.

    Google Scholar 

  15. Lenschow, D.H. and Stephens, P.L., The role of thermals in the convective boundary layer, Bound.-Layer Meteor., 1980, vol. 19, no. 4, pp. 509–532.

    Article  Google Scholar 

  16. Lenschow, D.H., Wyngaard, J.C., and Pennell, W.T., Mean field and second-moment budgets in a baroclinic, convective boundary layer, J. Atmos. Sci., 1980, vol. 37, no. 6, pp. 1313–1326.

    Article  Google Scholar 

  17. Levine, J., Spherical vortex theory of bubble-like motion cumulus clouds, J. Meteor., 1959, vol. 16, no. 6, pp. 653–662.

    Article  Google Scholar 

  18. Luhar, A.K. and Britter, R.E., A random walk model for dispersion in inhomogeneous turbulence in a convective boundary layer, Atm. Environ., 1989, vol. 23, pp. 1911–1924.

    Article  Google Scholar 

  19. Ogura, Y. and Phillips, N.A., Scale analysis of deep and shallow convection in the atmosphere, J. Atmos. Sci., vol. 32, no. 2, pp. 173–179.

  20. Pope, S.B., Turbulent Flows, Cambridge: Cambridge Univ. Press, 2000.

    Book  Google Scholar 

  21. Priestly, C.H.B., Turbulent Transfer in the Lower Atmosphere, Chicago: Univ. Chicago Press, 1959.

    Google Scholar 

  22. Schmidt, H. and Schumann, U., Coherent structure of the convective boundary layer derived from large-eddy simulations, J. Fluid Mech., 1989, vol. 200, pp. 511–562.

    Article  Google Scholar 

  23. Scorer, R.S. and Ludlam, F.H., Bubble theory of penetrative convection, Quart. J. R. Meteorol. Soc., 1953, vol. 79, pp. 94–106.

    Article  Google Scholar 

  24. Shin, H.H., Hong, S.-Y., and Noh Y., Derivation of turbulent kinetic energy from a first-order nonlocal planetary boundary layer parameterization, J. Atmos. Sci., 2013, vol. 70, pp. 1795–1805.

    Article  Google Scholar 

  25. Sparow, E.M., Husar, R.B., and Goldstein, R.J., Observation and other characteristics of thermals, J. Fluid Mech., 1970, vol. 41, no. 4, pp. 793–800.

    Article  Google Scholar 

  26. Turner, J.S., Buoyancy Effects in Fluids, Cambridge: Cambridge Univ. Press, 1979.

    Google Scholar 

  27. Van Kampen, N.G., Stochastic Processes in Physics and Chemistry, Amsterdam: North Holland: Elsevier, 2007.

    Google Scholar 

  28. Vulfson, A.N. and Borodin, O.O., Brownian ensemble of random-radius buoyancy vortices and Maxwell velocity distribution in a turbulent convective mixed-layer, Phys. Fluids, 2018, vol. 30. 095103. https://doi.org/10.1063/1.5042676

    Article  Google Scholar 

  29. Vul’fson, A.N. and Borodin, O.O., Maxwell velocity distribution for a stochastic ensemble of thermals in a turbulent convective mixed-layer, Kinet. Appr. Procedia IUTAM, 2013, vol. 8, pp. 238–247.

    Article  Google Scholar 

  30. Willis, G.E. and Deardorff, J.W., A laboratory model of the unstable planetary boundary layer, J. Atmos. Sci., 1974, vol. 31, pp. 1297–1307.

    Article  Google Scholar 

Download references

Funding

This study was carried out under research project 0147-2019-0001, state registration АААА-А18-118022090056-0).

Author information

Authors and Affiliations

  1. Water Problems Institute, Russian Academy of Sciences, 117701, Moscow, Russia

    A. N. Vul’fson & O. O. Borodin

  2. National Research University Higher School of Economics, 101000, Moscow, Russia

    A. N. Vul’fson & D. O. Demin

Authors
  1. A. N. Vul’fson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. O. Borodin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. O. Demin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to A. N. Vul’fson, O. O. Borodin or D. O. Demin.

Additional information

Translated by G.Krichevets

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vul’fson, A.N., Borodin, O.O. & Demin, D.O. An Ensemble of Brownian Particles and a Stochastic Description of a System of “Slow” Convective Thermals at Convection Level. Water Resour 49, 212–222 (2022). https://doi.org/10.1134/S0097807822020130

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0097807822020130

Keywords:

Search

Navigation