Introduction

Load serving entity (LSE) acts as a mediator between consumers and wholesale electricity market (WEM), to fulfill consumer demand by purchasing from WEM. LSE intends to maximize its profit through decisions on electricity procurement and offered sale prices. These decisions are taken well in advance to maximize the difference between revenue from electricity sale and procurement cost from WEM. Making prudent decisions for profit maximization is challenged by various factors associated at retail and wholesale levels of electricity markets. LSE’s market share would vary in competitive retail electricity markets as it depends on offered sale price [1]. However, retail competition is weak and characterized by low consumer switching rate in several markets. Only consumers with high price elasticity change their demand in response to offered retail prices [2]. Price elasticity is low in certain markets, indicating consumer’s rigidity to change their energy consumption [2]. Low elasticity restricts sufficient demand response. However, due to various known and unknown factors, demand varies continuously and is uncertain. At real-time, LSE may face different market conditions from those estimated some time ahead; hence its medium-term decisions are influenced by demand and pool price uncertainties [1, 3]. Modeling of demand and pool price uncertainty improves LSE’s decisions to reduce their impact on targeted profit. However, co-variation of consumer demand and prices associated with these uncertainties can create severe situations, and LSE may face significant financial losses. Such extreme risks needs to be considered and modeled for prudent decision-making.

Demand and pool prices are correlated due to their inherent dependence [4, 5]. Strength of this correlation depends upon LSE size. This correlation is weak for an LSE with low demand, in particular small retailers [6, 7]. However, for a large sized LSE, strong correlation is observed between demand and pool prices [6]. This correlation highlights possibility of extreme situations, which may cause substantial financial losses to LSE. Consideration of correlated variations of demand and pool prices can help to secure LSE’s position in the electricity market and improve it’s profit margin [3]. This correlation modeling is however challenging. Correlation between demand and pool prices can be modeled by scenario tree approach under a stochastic framework for LSE’s decision-making [7, 8]. However, scenario tree cannot consider severe uncertainty, and extreme situations (spikes) pronounced in higher frequency at hourly level, and may lead to imprudent decisions. Further, this method suffers when strong correlation exists between modeled variables [7]. Such issues with existing frameworks necessitate a novel framework to model demand and pool price uncertainties, along with their correlation.

LSE may emphasize on certain aspects of markets to maximize its profit. Such aspect could diversify the nature of LSE’s problem. The consideration may neglect other required aspect to highlight. For example, LSE may meticulously utilize short-term contracts and flexible demand to manage its strategy in electricity markets [9]. To modulate demand side response for increasing its profit [10] When flexible demand is available to LSE, a price-maker LSE’s bidding and sale price decisions require strategic modifications to secure profit [11, 12]. LSE’s participation in renewable energy markets necessitates development of its profit strategies considering renewable factors [13]. This implies that though other factors could affect LSE’s profit maximization decision making, consideration of price and demand uncertainty cannot be neglected. Most decision-making approaches for LSE characterize uncertainties by probabilistic or possibilistic approaches utilizing probability density function (PDF) or membership function (MF) [14, 15]. A large number of generated scenarios need to be reduced to a smaller number to keep the problem tractable [13]. Function modeling requires significant information about uncertain input parameters [16]. However, with a lack of information about PDF and MF, opted assumptions may lead to imprudent decisions [17, 18]. Moreover, a risk measure is required to assess the risk posed by the uncertainties [19, 20]. Downside risk constraints method utilizes probabilistic framework to assess the risk [21]. This method scarcely improves the decisions under lack of information about uncertain parameters. Information Gap Decision Theory (IGDT) is an effective and widely accepted approach to model severe uncertainties under lack of information [22, 23]. LSE’s power purchasing portfolio is devised using IGDT [24]. IGDT has been applied with integral modeling of demand and pool price uncertainties for LSE. Fractional error bound info-gap model can model these uncertainties to obtain robust strategies. In particular, demand and pool price uncertainties are considered by multi-objective Pareto optimal solutions [25, 26]. However, these research do not model demand and pool price uncertainties in a single framework, hence cannot consider co-variations existing between them. This makes LSE’s profit maximization decision-making modeling incomplete.

Wider research on LSE’s profit maximization considers various aspects which could possibly impacts its strategies for profit making in electricity markets [13, 15]. Substantial focus is given to uncertainty modeling of one or more uncertain parameters [21, 27]. However, modeling of correlation between price and demand uncertainty is not addressed adequately by the current literature, while decision-making for LSE’s profit maximization. This work proposes a novel integrated framework to model LSE’s decision-making using IGDT to maximize its profit under uncertainty of consumer demand and pool prices. Proposed model is suitable for evolving market conditions where LSEs are large, and consumer switching is low. Available information of varying consumer demand and pool prices, along with their correlation, is used in ellipsoid-bound info-gap uncertainty model. Adverse and favorable conditions arising due to varying consumer demand and pool prices are modeled to make robust and opportunistic decisions. This way, IGDT addresses risk-averse and risk-seeking behavior of LSE. Impact of multiple severe uncertainties has been highlighted for LSE’s electricity procurement and sale price, separately for weekdays and weekends. Results indicate that capturing demand and price uncertainties together helps LSE to make prudent decisions. Thus, this work contributes by

  • Modeling correlated demand and pool prices in an integrated framework considering their severe uncertainty using ellipsoid bound info-gap uncertainty model

  • Modeling and analysis of robustness and opportunistic decisions in single framework of correlated demand and pool price

LSE’S Decision-making Problem

LSE’s primary role is to procure electricity on behalf of consumers from wholesale markets and supply them at contracted/ predefined sale prices under various tariff schemes. Traditionally, energy services were provided by distribution companies (DisCos) and currently by retailers. DisCos are responsible for network operation whereas retailers deal with electricity trading. Therefore, these entities are termed as LSE.

LSE’s sale prices and procurement strategies decision-making model requires knowledge of consumer’s elastic behavior and level of retail competition1. In evolving retail electricity markets, significant market share is served by incumbent LSE. Consumers are reluctant to switch to a new entrant LSE for the risk of an unexpected rise in electricity bill. Consumers observe switching as complex process invloving time and money for which the benefit is not guaranteed [28]. This results in low switching rate, indicating weak competition. Therefore, LSE’s market share is hardly impacted in such markets, but due to large share of demand, impact of correlation becomes significant on its decisions.

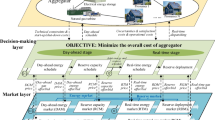
This work intends to determine decisions of a large LSE considering integrated modeling of correlated demand and prices. LSE fulfill its requirement through procurement from WEM via pool and bilateral contracts, and from self-generation facility. Market liquidity is assumed sufficient. Bilateral contract prices are fixed, and cost of self-generation is known at the time of decision-making. This advance planning problem of LSE is considered in the medium-term to determine optimal energy procurement strategy and sale prices. A framework is proposed to model both pool prices and demand uncertainties with their correlated variations using ellipsoid-bound model of uncertainty under IGDT. LSE’s decision-making model in IGDT framework is shown in Fig. 1. Risk-averse and risk-seeking behavior of LSE is addressed by modeling its profit maximization problem using robustness and opportunity functions, respectively. The joint impact of pool price and demand uncertainty is addressed by single uncertainty horizon in the framework. This helps to analyze the correlation impact for weekdays and weekends.

Fig. 1
figure 1

LSE’s decision-making model

Full size image

In this paper, term ”LSE” represents retailer’s or DisCo’s market operation (trading) only, i.e., network operation is neglected to highlight their market strategies required for profit maximization. This work considers that LSE does not control consumers’ demand directly, but it is result of offered sale prices. Therefore, considering the focus of the proposed work, consumers’ active participation and its comfort modeling in LSE’s decision-making is not desirable.

Mathematical Formulation of LSE’s Profit Maximization

LSE’s profit maximization problem is mathematically formulated, and the two components of profit: procurement cost and revenue, are described as follows.

Procurement Cost

LSE’s procurement cost at hour t is the sum of cost of energy procured from bilateral contracts, self-generation, and pool represented in Eq. 1. The proposed problem intends to optimize procurement decisions, hence costs relevant to staff, billing system, advertising, etc. are neglected.

$$ Cost_{t}^{total}={C_{t}^{B}}+C_{t}^{SG}+{C_{t}^{S}} $$
(1)

Bilateral Contract Cost

LSE signs bilateral contracts with generating companies at a mutually agreed fixed price \(\lambda _{i,t}^{B}\) for a specified time t [3]. Let total number of available bilateral contracts be I. The energy procurement cost from all bilateral contracts \({C_{t}^{B}}\) at hour t is given by Eq. 2. Minimum and maximum limits on procurement from bilateral contracts are considered by constraint (3).

$$ {C_{t}^{B}}=\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}} $$
(2)
$$ P_{i}^{\min}.{{\delta }_{i,t}}\le P_{i,t}^{B}\le P_{i}^{\max}.{{\delta }_{i,t}} $$
(3)

Self-generation Cost

LSE uses self-generation to procure a portion of its demand. All units are considered as thermal units only. At time t, total energy procured from G self-generating units would be equal to

$$ P_{t}^{SG}=\sum\limits_{g\in G}{P_{g,t}^{SG}} $$
(4)

Generation cost Cg, t of \(P_{g,t}^{SG}\) energy from gth generating unit in hour t is given by Eq. 5, subject to constraints (6) to (14) [3].

$$ C_{g,t}^=c.{{u}_{g,t}}+b.P_{g,t}^{SG}+a.{{(P_{g,t}^{SG})}^{2}}+c_{g,t}^{su}+c_{g,t}^{sd} $$
(5)
$$ c_{g,t}^{su}\ge C_{g}^{su}({{u}_{g,t}}-{{u}_{g,t-1}})\quad \quad \quad \quad \forall g,\forall t $$
(6)
$$ c_{g,t}^{sd}\ge C_{g}^{sd}({{u}_{g,t-1}}-{{u}_{g,t}})\quad \quad \quad \quad \forall g,\forall t $$
(7)
$$ P_{g,t}^{SG}-P_{g,t-1}^{SG}\le {R_{g}^{u}}.{{u}_{g,t}}\quad \quad \quad \ \quad \forall g,\forall t $$
(8)
$$ P_{g,t-1}^{SG}-P_{g,t}^{SG}\le {R_{g}^{d}}.{{u}_{g,t-1}}\quad \quad \quad \quad \forall g,\forall t $$
(9)
$$ [X_{g,t-1}^{ON}-{T_{g}^{U}}].[{{u}_{g,t}}-{{u}_{g,t-1}}]\ge 0\quad \forall g,\forall t $$
(10)
$$ [X_{g,t-1}^{OFF}-{T_{g}^{D}}].[{{u}_{g,t-1}}-{{u}_{g,t}}]\ge 0\quad \forall g,\forall t $$
(11)
$$ P_{g}^{min}.{{u}_{g,t}}\le P_{g,t}^{SG}\le P_{g}^{max}.{{u}_{g,t}}\quad \ \quad \forall g,\forall t $$
(12)
$$ c_{g,t}^{su},c_{g,t}^{sd}\ge 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \forall g,\forall t $$
(13)
$$ {{u}_{g,t}}\in [0,1]\quad \quad \quad \quad \quad \quad \quad \quad \quad \forall g,\forall t $$
(14)

Constraints (6) and (7) decide start up and shut down cost of self-generating units. Constraints (8) and (9) decide ramp up and ramp down limits. Minimum up and down time of generating units is given by constraints (10) and (11). Minimum and maximum generation limits are decided by constraint (12). Equation 13 is a non-negativity constraint. Equation 14 is variable declaration constraint. The total generation cost from self-generating units is given by

$$ C_{t}^{SG}=\sum\limits_{g\in G}{C_{g,t}} $$
(15)

Pool Cost

LSE uses pool as one of the procurement options. As pool prices are uncertain, its forecasted/expected values are considered. Expected energy procurement cost from pool for each period t is

$$ {C_{t}^{S}}={P_{t}^{S}}{\lambda_{t}^{S}} $$
(16)

As this work addresses medium-term decision-making of LSE, constraint (17) is considered to restrict energy sale in pool at hour t. However, energy selling in the pool is required to settle residual energy imbalances. This decision is made nearer to real-time, and comes under short-term decision-making. Energy balance constraint (18) restricts energy procured from various sources to match consumer demand Pt at hour t.

$$ {P_{t}^{S}}\ge 0 $$
(17)
$$ {P_{t}^{S}}+\sum\limits_{i\in I}{P_{i,t}^{B}}+P_{t}^{SG}=P_{t} $$
(18)

Revenue

LSE generates revenue by selling energy to its group of consumers at offered sale prices \(\lambda _{t}^{sale}\). Revenue for each time slot is [8]

$$ Revenu{{e}_{t}}={{P}_{t}}\lambda_{t}^{sale} $$
(19)

Constraint (20) restricts LSE’s sale prices within the minimum and maximum bounds. Maximum bound is required to restrict LSE from increasing sale prices beyond a justified limit. Inequality constraint (21) is used as a bound on the average sale prices to ensure sufficient number of low price periods. Otherwise, LSE would always charge maximum possible from consumers [29].

$$ \lambda_{t}^{min}\le \lambda_{t}^{sale}\le \lambda_{t}^{max} $$
(20)
$$ \frac{\sum\limits_{t}{{{P}_{t}}\lambda_{t}^{sale}}}{\sum\limits_{t}{{P}_{t}}}\le \lambda^{avg} $$
(21)

Profit Function

LSE’s expected profit is calculated by subtracting procurement cost (1) from revenue generated from electricity sale (19), as shown in Eq. 22. Equation 23 is obtained by substituting values of revenue and cost terms in Eq. 22.

$$ Prof=\pi (P,\lambda )=\sum\limits_{t}{Revenu{{e}_{t}}}-\sum\limits_{t}{Cost_{t}^{total}} $$
(22)
$$ \begin{array}{@{}rcl@{}} Prof&=&\pi (P,\lambda )= \sum\limits_{t}{{{P}_{t}}\lambda_{t}^{sale}}\\ &&-\left( \sum\limits_{t}{{P_{t}^{S}}{\lambda_{t}^{S}}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right) \end{array} $$
(23)

It is to be noted in Eq. 23 that Pt and \({\lambda _{t}^{S}}\) are uncertain parameters that need to be handled. Due to their correlated nature, uncertainties are modeled in IGDT framework.

LSE’S Decision-making: IGDT Framework

IGDT quantifies uncertainty to help decision-maker evaluate decisions in an uncertain environment by utilizing available information about uncertain parameters. IGDT does not require a membership or probability functions to model uncertain parameters. IGDT models uncertainty as a variation interval between what is known and what could be known [17]. IGDT assesses performance requirements for decisions based on targeted/anticipated outcomes by robustness and opportuneness functions addressing risk-averse or risk-seeking behavior of a decision-maker. As IGDT is performance satisfying rather than performance maximizing approach [17], decision variables obtained from this approach are not comparable with conventional uncertainty and risk handling approaches. Also, it is worth to note that performance satisfying and input parameters to optimization, differ atleast IGDT from robust optimization (RO) [30]. RO is a performance maximizing approach, which handles only worst condition arising due to uncertain parameters [31]. Sometimes, IGDT is compared with interval analysis method of uncertainty modeling. However, interval analysis characterizes uncertain parameters based on a known interval, which differentiates it from IGDT.

System model, performance requirements, and uncertainty model are three components of IGDT that can describe decision problems. System model expresses the input and output relationship of the system considering decision variables, uncertainty parameter, and uncertain parameter. Requirement of performance describes the requirements or expected outcomes from the system. It is usually expressed in terms of cost or relevant functions. Robustness and opportunity functions are evaluated to describe these requirements. These functions are explained in subsequent sections. Various uncertainty models are available to adequately model the uncertain parameters. These models utilize available information about uncertain input parameters Uncertainty model expresses the gap between known and unknown values as function of some known parameters. The known parameters could be predicted or forecasted value of uncertain parameter, variance-covariance matrix or standard deviation etc. [17].

In this work, IGDT models demand and pool price uncertainties and their co-variability. Modeling of uncertain demand and pool prices in a single framework is proposed by considering a single uncertainty horizon under ellipsoid-bound info-gap uncertainty model. This info-gap uncertainty model is considered as it models correlation between uncertain parameters in the form of variance and co-variance matrix. This is discussed in Section “Uncertainty Model”. Immunity from unfavorable movements and opportunity of windfall gain for favorable movements of demand and pool prices are determined by formulating robustness and opportuneness formulations, respectively. The mathematical model based on IGDT approach is presented in following sub-sections.

Decision Variables

As per (23), sale price \(\lambda _{t}^{sale}\) and the quantum of energy to be procured from various resources (pool \({P_{t}^{S}}\), bilateral contracts \(P_{i,t}^{B}\), and self-generation \(P_{t}^{SG}\)) are decision variables of the problem, and are represented as \({{Q}_{t}}=\left [ \lambda _{t}^{sale},\ {P_{t}^{S}},\ P_{i,t}^{B},\ \ P_{t}^{SG} \right ]\).

Uncertainty Model

Uncertainty of total demand Pt to be procured and pool prices \({\lambda _{t}^{S}}\), at hour t is modeled through ellipsoid bound info-gap uncertainty model. These uncertain parameters are represented by a vector xt in Eq. 24. At real-time, actual values of uncertain parameters may vary from their estimates \({{\tilde {x}}_{t}}\) in either direction (positive or negative) by an error Δxt (25).

$$ {{x}_{t}}=[{{P}_{t}},{\lambda_{t}^{S}}] $$
(24)
$$ {{x}_{t}}={{\tilde{x}}_{t}}+{\Delta} {{x}_{t}} $$
(25)

i.e.,

$$ [{{P}_{t}},{\lambda_{t}^{S}}]=[{{\tilde{P}}_{t}}+{\Delta} {{P}_{t}},\ \tilde{\lambda }_{t}^{S}+{\Delta} {\lambda_{t}^{S}}] $$
(26)
$$ {\Delta} {{x}_{t}}=[{\Delta} {{P}_{t}},\ {\Delta} {\lambda_{t}^{S}}] $$
(27)

Ellipsoid-bound info-gap model considers uncertainty by an unbounded family of nested sets, nested around expected value of the parameter of interest. Each set represents a particular degree of knowledge deficiency, depending upon the level of nesting [17]. Ellipsoid is an envelop of uncertainty, and that is centered around best estimate vector \({{\tilde {x}}_{t}}\), with a distance represented by uncertainty horizon α. This ellipsoid quantifies the uncertainty by measuring distance between best estimate and reality (actual value), as shown in Fig. 2. Larger the distance, larger is the uncertainty α (Fig. 2). The shape of ellipsoid describes the relative degree of variability of demand and pool prices and their correlated behavior [17]. A variance-covariance matrix W defines this information. Here, in case of two uncertain parameters, Pt and \({\lambda _{t}^{S}}\), W is a 2 × 2 matrix for each time interval t. Its elements, w11 and w22 are variances of Pt and \({\lambda _{t}^{s}}\) respectively, and w12 = w21 are co-variances between them. This information is statistically obtained from historical data. Mathematically ellipsoid bound info-gap model is given as [17]

$$ U(\alpha ,{{x}_{t}})=\{{{x}_{t}}:{\Delta} {{x}_{t}}{{W}^{-1}}{\Delta} {{x}_{t}}^{\prime}\le {{\alpha }^{2}}\},\ \ \alpha \ge 0 $$
(28)

Here ′ represents transpose.

Fig. 2
figure 2

Pictorial presentation of Ellipsoid bound-info gap model

Full size image

Performance Functions

Performance requirements are the minimum requirements expected or anticipated from the system, evaluated based on robustness and opportuneness functions. Robustness function immunes the decision-maker from adverse face of the uncertainty, whereas opportuneness function offers opportunity to decision-maker from favorable situations.

Robustness function calculates the highest level of uncertainty that can be tolerated by a decision for which minimum requirements are always satisfied. Robustness guarantees that the profit would always be greater than targeted critical profit πc so that certain level of uncertainty can be tolerated. Hence, this represents risk-averse behavior of decision-maker. Mathematically, robustness \(\hat {\alpha }({{\pi }_{c}})\) can be expressed as [17, 26]

$$ \hat{\alpha }({{\pi }_{c}})=\underset{\alpha }{\mathop{\max }} \{\alpha :min\ \pi (Q,x)\ge {{\pi }_{c}}\} $$
(29)

Opportuneness function evaluates the possibility of achieving higher profit resulting from favorable face of uncertainty and provides windfall benefits. It addresses risk-seeking attitude of a decision-maker. The opportuneness function expresses the least required level of uncertainty (i.e., uncertainty horizon α) for which windfall profit πw can always be achieved. Mathematically, opportuneness \(\hat {\beta }({{\pi }_{w}})\) is expressed as [17, 26]

$$ \hat{\beta }({{\pi }_{w}})=\underset{\alpha }{\mathop{\min }} \{\alpha :max\ \pi (Q,x)\ge {{\pi }_{w}}\} $$
(30)

Robustness Function

As per the robustness function defined in Eq. 29, minimum profit should at least be equal to πc [13]. Minimum profit is determined by substituting (26) and (28) in (23). This yields (31).

$$ \begin{array}{@{}rcl@{}} \underset{\Delta {{x}_{t}}}{\mathop{\min }} Prof&=& \sum\limits_{t}{({{{\tilde{P}}}_{t}}+{\Delta} {{P}_{t}})\lambda_{t}^{sale}}- \left( \sum\limits_{t}{{P_{t}^{S}}(\tilde{\lambda }_{t}^{S}+{\Delta} {\lambda_{t}^{S}})}\right.\\ &&\left.+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right) \end{array} $$
(31)

s.t.

$$ {\Delta} {{x}_{t}}{{W}^{-1}}{\Delta} {{x}_{t}}^{\prime}\le {{\alpha }^{2}} $$
(32)

Equations 31 and 32 can be simplified and given by Eq. 33.

$$ \begin{array}{@{}rcl@{}} \underset{\Delta {{x}_{t}}}{\mathop{\min }} Prof&=&\sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}}-\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}\right.\\ &&\left.+\sum\limits_{t}{C_{t}^{SG}} \right) +\underset{\Delta {{x}_{t}}}{\mathop{\min }} \left\{ \sum\limits_{t}{\Delta {{P}_{t}}\lambda_{t}^{sale}}\right.\\ &&\left.-\sum\limits_{t}{{P_{t}^{S}}{\Delta} {\lambda_{t}^{S}}}:{\Delta} {{x}_{t}}{{W}^{-1}}{\Delta} {{x}_{t}}^{\prime}\le {{\alpha }^{2}} \right\} \end{array} $$
(33)

Substituting \({{y}_{t}}=[\lambda _{t}^{sale}\ \ -{P_{t}^{S}}]\) will give (34).

$$ \begin{array}{@{}rcl@{}} \underset{\Delta {{x}_{t}}}{\mathop{\min }} Prof& = &\sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}}-\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}\right.\\ &&\left. + \sum\limits_{t}{C_{t}^{SG}} \right) + \underset{\Delta {{x}_{t}}}{\mathop{\min }} \left\{ \sum\limits_{t}{\Delta {{x}_{t}}}{{y}_{t}}^{\prime}:{\Delta} {{x}_{t}}{{W}^{-1}}{\Delta} {{x}_{t}}^{\prime}\le {{\alpha }^{2}} \right\} \end{array} $$
(34)

Using Lagrangian relaxation method for the convex optimization problem, first-order optimality condition is obtained as

$$ {{\nabla }_{\Delta {{x}_{t}},\mu }}\left\{ {\Delta} {{x}_{t}}{{y}_{t}}^{\prime}+\mu ({{\alpha }^{2}}-{\Delta} {{x}_{t}}{{W}^{-1}}{\Delta} {{x}_{t}}^{\prime}) \right\}=0 $$
(35)

where μ is Lagrange multiplier. Derivatives of Eq. 35 result in

$$ {{y}_{t}}^{\prime}-2\mu W_{t}^{-1}{\Delta} {{x}_{t}}^{\prime}=0 $$
(36)
$$ {{\alpha }^{2}}-{\Delta} {{x}_{t}}W_{t}^{-1}{\Delta} {{x}_{t}}^{\prime}=0 $$
(37)

Simplification of Eqs. 36 and 37 would result in

$$ {\Delta} {{x}_{t}}^{\prime}=\frac{1}{2\mu }{{W}_{t}}{{y}_{t}}^{\prime}\ \text{and}\ {{\alpha }^{2}}={\Delta} {{x}_{t}}W_{t}^{-1}{\Delta} {{x}_{t}}^{\prime} $$
(38)

Simplifying (38) would result in

$$ {{\alpha }^{2}}=\frac{1}{2\mu }{{W}_{t}}{{y}_{t}}W_{t}^{-1}\frac{1}{2\mu }{{W}_{t}}{{y}_{t}}^{\prime}=\frac{1}{4{{\mu }^{2}}}{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime} $$
(39)

Simplifying (39) would result in

$$ \frac{1}{2\mu }=\pm \frac{\alpha }{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}} $$
(40)

Equations 38 and 40 can be rewritten as

$$ {\Delta} {{x}_{t}}=\pm \alpha \frac{{{y}_{t}}{{W}_{t}}}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}} $$
(41)

Equations 39 and 40 can be rewritten as

$$ {\Delta} {{x}_{t}}{{y}_{t}}^{\prime}=\pm \alpha \sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}} $$
(42)

Considering negative value from Eq. 42, to evaluate minimum profit in Eq. 34 as shown in Eq. 43.

$$ \begin{array}{@{}rcl@{}} \underset{\Delta {{x}_{t}}}{\mathop{\min }} Prof&=&\sum\limits_{t}{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}-\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in B}{P_{i,t}^{B}\lambda_{i,t}^{B}}}\right.\\ &&\left.+\sum\limits_{t}{C_{t}^{SG}} \right) -\left\{ \alpha \sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}} \right\} \end{array} $$
(43)

Hence, Eq. 43 can be rewritten as shown in Eq. 44.

$$ \begin{array}{@{}rcl@{}} \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}}&-&\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right) \\ &-&\left\{ \alpha \sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}} \right\}={{\pi }_{c}} \end{array} $$
(44)

Hence, the value of uncertainty α at πc can be defined by Eq. 45.

$$ \alpha ({{\pi }_{c}})= \\ \frac{\left\{ \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}}-\left( \sum\limits_{t}{{P_{t}^{S}}{\lambda_{t}^{S}}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right) \right\}-{{\pi }_{c}}}{\sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}}} $$
(45)

So the maximum value of uncertainty which can be tolerated to achieve minimum profit πc is given by Eq. 46.

$$ \hat{\alpha }({{\pi }_{c}})= \\ \underset{{{Q}_{t}}}{\mathop{\max }} \frac{\left\{ \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}-\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in B}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right)} \right\}-{{\pi }_{c}}}{\sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}}} $$
(46)

Opportunity Function

Opportunity function evaluates the least level of uncertainty so that profit can be as large as πw [17]. Steps present in Section “Robustness Function” can be followed to derive opportunity function. As per Eq. 30, opportunity function (47) can be derived by positive value of \({\Delta } {{x}_{t}}{{y}_{t}}^{\prime }\) and equating it to πw.

$$ \begin{array}{@{}rcl@{}} \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}}&-&\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}}+\sum\limits_{t}{C_{t}^{SG}} \right) \\ &&+\left\{ \alpha \sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}} \right\}={{\pi }_{w}} \end{array} $$
(47)

Value of uncertainty horizon α at anticipated windfall profit πw is defined by Eq. 48.

$$ \begin{array}{@{}rcl@{}} \beta ({{\pi }_{w}})=\frac{{{\pi }_{w}}-\left\{ \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale}-\left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}}+\sum\limits_{t}{\sum\limits_{i\in I}{P_{i,t}^{B}\lambda_{i,t}^{B}}+}\sum\limits_{t}{C_{t}^{SG}} \right)} \right\}}{\sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}}} \end{array} $$
(48)

Opportuneness is the minimum uncertainty required to obtain profit as large as πw, which can be defined by Eq. 49.

$$ \begin{array}{@{}rcl@{}} \hat{\beta }({{\pi }_{w}}) = \underset{{{Q}_{t}}}{\mathop{\min }} \frac{{{\pi }_{w}} - \left\{ \sum\limits_{t}{{{{\tilde{P}}}_{t}}\lambda_{t}^{sale} - \left( \sum\limits_{t}{{P_{t}^{S}}\tilde{\lambda }_{t}^{S}} + \sum\limits_{t}{\sum\limits_{i\in B}{P_{i,t}^{B}\lambda_{i,t}^{B}}+}\sum\limits_{t}{C_{t}^{SG}} \right)} \right\}}{\sum\limits_{t}{\sqrt{{{y}_{t}}{{W}_{t}}{{y}_{t}}^{\prime}}}} \end{array} $$
(49)

Derived robustness function (46) has to be maximized, whereas opportuneness function (49) has to be minimized subject to the same set of constraints represented in Eqs. 1 to 21. The values of πc and πw are determined by risk neutral profit maximization problem posed by Eq. 23, subject to constraints (1) to (21). The procedure discussed above is summarized in Fig. 3. Here, ’s’ is step size for which ’n’ values of πc and πw are determined.

Fig. 3
figure 3

Flowchart describing procedure

Full size image

Case Study

The proposed model for a large LSE is illustrated via a case study. Demand and pool prices for weekend and weekdays are considered in two sub-cases to analyze LSE’s decision-making. For medium-term planning period and considering each hour of a day as a sale price time block, robust and opportunity strategies are determined and presented.

Data

Historical demand and pool price data from Nord Pool of West Denmark area are considered for this study [32]. This data is used to produce predicted values of demand and pool prices for weekend and weekday (Fig. 4). Bilateral contracts at fixed price of 31.5 $/MWh and 39 $/MWh, with maximum trading limits of 1300 MW and 1550 MW are considered for weekend and weekday, respectively. A minimum procurement of 10 MW from bilateral contract is considered for both cases. LSE also has a self-generation facility of capacity 130 MW. Average sale prices of 40.5$ and 34.5$ for weekday and weekend are considered.

Fig. 4
figure 4

Demand and pool price curve for weekday (Mon.) and weekend (Sun.)

Full size image

Statistical Calculations

Variance-covariance matrix W is calculated from historical demand and pool price data for each day of a week over a season for each t. Positive correlation is observed between demand and pool price for weekdays, whereas varying positive and negative correlations are observed for weekends. Negative correlation indicates that demand and pool prices vary in opposite direction. Based on these observations, Monday from weekday and Sunday from the weekend, are selected for case study to analyze impact of correlation on LSE’s decision-making. A representation of covariances in terms of correlation between pool price and demand is shown in Fig. 5 for weekend and weekdays.

Fig. 5
figure 5

Correlation between pool price and demand for weekday (Mon.) and weekend (Sun.)

Full size image

Simulations

The profit maximization problem is simulated for (23), subject to constraints (1)–(21), for the considered data. Based on the predicted value of pool price \(\tilde {\lambda }_{t}^{S}\) and demand \({{\tilde {P}}_{t}}\), optimization provides the maximum possible value of profit \(\tilde {\pi }(\tilde {P},{{\tilde {\lambda }}^{S}})\). This case shows evaluated decisions without considering demand and pool price uncertainties, implying risk-neutral behavior of LSE. Considering this maximum profit \(\tilde {\pi }(\tilde {P},{{\tilde {\lambda }}^{S}})\), critical profit targets πc and anticipated windfall gains πw are assumed in small steps. For robustness function, critical profit targets are considered less than \(\tilde {\pi }(\tilde {P},{{\tilde {\lambda }}^{S}})\). For opportunity function, anticipated windfall profits are considered higher than \(\tilde {\pi }(\tilde {P},{{\tilde {\lambda }}^{S}})\).

For each value of critical profit πc and windfall gain πw, decision variable Qt is obtained by optimizing (46) and (49), subject to constraints (1)–(21). All the analysis and simulations are performed separately for weekdays and weekends.

The three optimization problems are MINLP in nature and solved using SBB/CONOPT solver under GAMS26. SBB uses the standard branch and bound algorithm for node selections. The NLP solver CONOPT utilizes solution obtained from SBB to optimize NLP problem [33]. The proposed model for LSE has 265 real and 48 discrete variables. Simulations are carried out in an Intel®; Core™ i7, 2 GHz processor and 8 GB of RAM system. Average execution and computation time to solve robust optimization problems for robustness are 0.253s & 10.31s and opportuneness are 0.3622s and 10.067s, respectively.

Results

The risk-neutral maximum value of profit \(\tilde {\pi }(\tilde {P},{{\tilde {\lambda }}^{S}})\) for weekday and weekend obtained by simulations are 304679.45$ and 263705.97$, respectively. These are the maximum profits that can optimally be attained by LSE. The relevant quantum of energy procured from the pool, bilateral contracts, and self-generation are shown in Table 1. Hourly sale prices obtained are depicted in Fig. 6. The sale prices follow the trend of pool prices.

Table 1 Energy procurement from various sources
Full size table
Fig. 6
figure 6

Sale prices for risk-neutral LSE

Full size image

For case study, values of πc varying from 304679.45 to 225462.79$ and from 263705.97 to 195142.42$ for weekdays and weekends, respectively, are considered. Values of πw that vary from 304679.45 to 457019.19$ and from 263705.97 to 421929.55$ for weekday and weekends, respectively, are considered. The results obtained from simulations for each value of πc and πw for robustness and opportunity functions are shown collectively in Figs. 7, 8, 9 and 10. Curve on left-hand side of the marker indicates outcomes related to robustness, and the right ones are related to opportuneness.

Fig. 7
figure 7

Robustness and opportuneness curves for critical and anticipated targets

Full size image
Fig. 8
figure 8

Energy procurement from different sources for (a) weekday and (b) weekend

Full size image
Fig. 9
figure 9

Expected cost for weekend and weekday

Full size image
Fig. 10
figure 10

Expected profit for different targeted profit for critical and anticipated targets

Full size image

Robust Strategy

Results show that as the value of critical profit target πc reduces (when it shifts left from the market), obtained decisions can tolerate higher uncertainties of pool price and demand (Fig. 7). Hence, robustness of a decision increases with reduced profit targets. LSE avoids uncertainty by increasing energy procurement from bilateral contracts and self-generation, while decreasing procurement from pool to make a decision robust (left side of Fig. 8). This enhances expected energy procurement cost, thus reducing expected profit. Increase in expected cost is due to increase in involvement of costly procurement options. The variation between expected cost and targeted profit for different values of robustness for weekdays and weekends is shown in Fig. 9. The figure shows that decrease in values of expected profit reflects the cost to attain robustness. The difference in slope of robust strategies for weekday and weekend highlights impact of correlation (Fig. 7). This is due to positive correlation for weekday and positive and negative for weekend.

Opportunistic Strategy

Right side of marker in Fig. 7 depicts the opportuneness curve. Y-axis defines the lowest required level of uncertainty α at which windfall gain πw (x-axis) is possible. The figure reflects that value of uncertainty increases with anticipated profit target. Energy procurement from the pool, bilateral contracts, and self-generation for weekday and weekend are depicted in Fig. 8. With increasing anticipated profit πw energy procurement from pool increases while procurement from bilateral contracts and self-generation decreases (Right side of Fig. 8). This happens because high variability is desired to achieve anticipated profit πw. As pool trading has high price variations, it possesses high windfall possibility. Highest uncertainty is obtained when procurement from bilateral contracts and self generation is minimal (πw= 45 × 104). Figure 8 indicates that procurement from self-generation and bilateral contracts becomes zero to attain maximal windfall gain. Figure 9 gives expected cost and Fig. 10 depicts expected value of profit for weekday and weekend. This indicates the cost of uncertainty, which represents that if anticipated deviation does not happen, expected profit will be less and cost would be higher than its maximum/minimum values. Highest cost is achieved when highest robustness is required (extreme left of Fig. 9) or when high opportunity is required (Extreme right of Fig. 9). Corresponding profits for these instances can be seen in Fig. 10. The difference in slope of opportunistic strategies for weekday and weekend highlights impact of correlation (Fig. 7). This is due to positive correlation for weekday and positive and negative for weekend.

For robustness and opportuneness, the dynamics of sale prices offered to the consumers is indicated in Fig. 11a. For robustness, high sale prices are offered during peak hours to cope with increased cost experienced due to increased procurement from fixed cost sources (bilateral contracts and self-generation). However, low sale prices are offered for opportunistic case during peak hours, as procurement from pool increases to exploit opportunity due to uncertainty. Low volatility in pool prices is experienced during hours 10 to 16; hence high and low sale prices are offered for opportuneness and robustness, respectively. This observation indicates that contrasting sale prices are a consequence of LSE’s risk-averse and risk-seeking behavior. It is worth to note here that consumer demand is considered inelastic.

Fig. 11
figure 11

Hourly sale price for (a) weekdays and (b) weekends

Full size image

The dynamics of sale prices offered for robustness (or opportuneness) case over weekend (Fig. 11b) differs from that offered for weekdays (Fig. 11a). Correlation between pool price and demand characteristics impacts sale prices obtained for robustness and opportuneness. Correlation is positive for weekdays over 24 hours while for weekend it is negative at certain hours (Fig. 5). For the hours when correlation is negative (Hour 11 to 17 and 19 to 23), both uncertainties compensate each other’s impact; hence overall impact would be less as compared to situations when correlation is positive. Therefore, sale prices are adjusted in a way to exploit maximum robustness and opportuneness.

Impact of Demand Uncertainty

Figure 12 indicates robustness and opportuneness curves considering (i) pool price uncertainty alone and (ii) pool and demand uncertainties together. Dotted line represents robustness and opportuneness curves considering both uncertainties. Solid line represents these curves when only pool price uncertainty is considered. The dotted curve lies above solid line curve, representing that for considered profit targets, tolerance for uncertainty is more when both the uncertainties are considered, than without considering demand uncertainty. Hence consideration of demand uncertainty helps to increase decision robustness. However, in case of opportuneness, for certain anticipated profit, higher uncertainty is required to achieve the same. This is because uncertain variations in demand and pool prices compensate each other’s impacts. Hence, demand uncertainty consideration is inevitable to achieve prudent decision-making for LSE. It is worth to note here that results are reflective of specific data set and their nature would vary depending upon market conditions.

Fig. 12
figure 12

Impact of demand uncertainty on robustness and opportuneness curves

Full size image

Conclusions

The paper proposes a novel framework for LSE’s profit maximization, considering demand and pool price uncertainties. The novelty of the work lies in modeling the correlation of demand and pool prices with their uncertainties, using ellipsoid-bound info-gap model. Risk-averse and risk-seeking behavior of LSE is modeled by robustness and opportuneness functions to achieve targeted profit. The proposed model is illustrated via a case study conducted for weekdays and weekends. The important results obtained from the proposed work are (1) Decisions for a risk-averse LSE, its decision become robust with lower profit targets, as tolerance for uncertainty increases. (2) High windfall profits are attained when large uncertainties are there in the uncertain parameters. (3) When correlation is positive and negative during certain periods of a day, it compensate for each other’s impact. (4) Impact of correlation on decisions is less when it is varying between positive and negative than when it is positive for each period of a day. (5) Tolerance of uncertainty increase when both price and demand uncertainties are considered (6) Consideration of the two uncertainties in a single framework helps to improve robustness of LSE’s decisions.

This work is helpful for LSE with a large demand. However, decisions of LSE with comparatively small demand would minimally benefit from the proposed work. This work can be extended to analyze the impact of renewable energy sources and energy storage on LSE’s decisions for profit maximization. Techno-economic aspects of a distribution company can be analyzed. Moreover, various consumer classes’ demand could be considered to determine strategies targeting that class.